Pneumonia dynamics

in bighorn sheep

Kezia Manlove

Dissertation defense

September 14, 2016

Pete

Raina Plowright

Paul Cross

Frances Cassirer

Tom Besser

Resource challenges in wildlife disease

Low public concern

Mortalities in captivity

Sub-optimal diagnostics

Rare longitudinal datasets

Rare post-mortems

Overarching challenge

Learn quickly from available data

Dissertation goals

1. Save sheep

2. Come up with a better plan

Introduction

Bighorn sheep pneumonia

Bighorn life history and ecology

long-lived, large-bodied

sexually dimorphic/live in sexually segregated groups

breed during fall rut

primiparity at age 2 (usually)

~170-day gestation period

rarely twin

diverged from Old World sheep ~ 5.6 mya

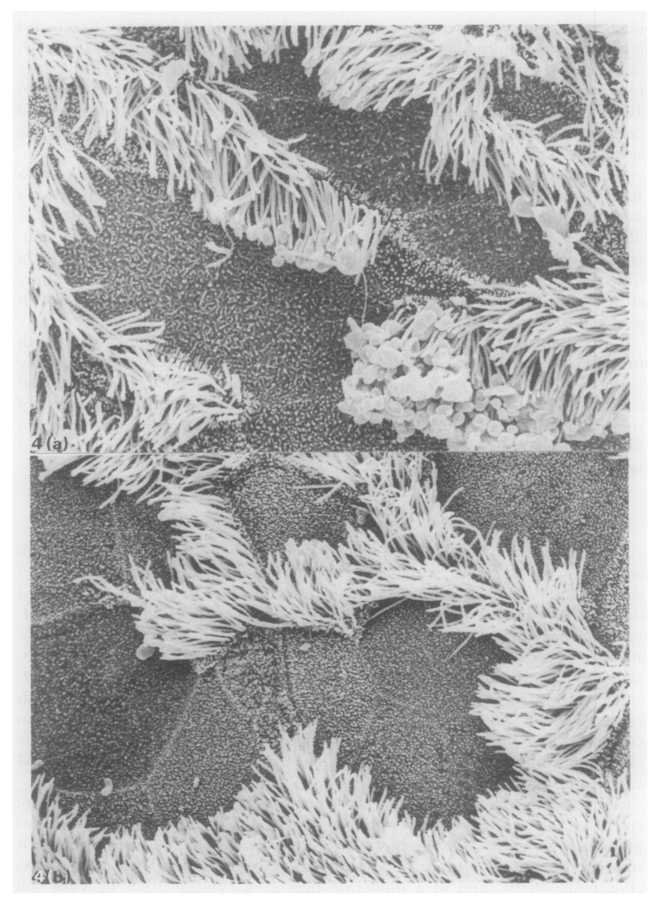
Healthy cilia

Cilia 10 dpi

Jones et al. (1985) Jo Comp Pathol

Besser et al. (2013) Prev Vet Med

Etiology and disease progression

Mycoplasma ovipneumoniaeExposure

Carriage

Upper

respiratory

tract

Lower respiratory tract

Clearance

Downward invasion

LRT

clearance

Between-host disease dynamics

Carrier

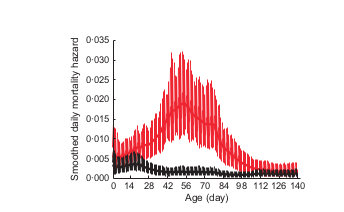
May 1

Sept 1

Daily lamb mortality hazard

Cassirer, Manlove et al. (2013) Jo Anim Ecol

0.035

0.000

Years with transmission

Years without transmission

Bighorn sheep status

Source: Wild Sheep Foundation

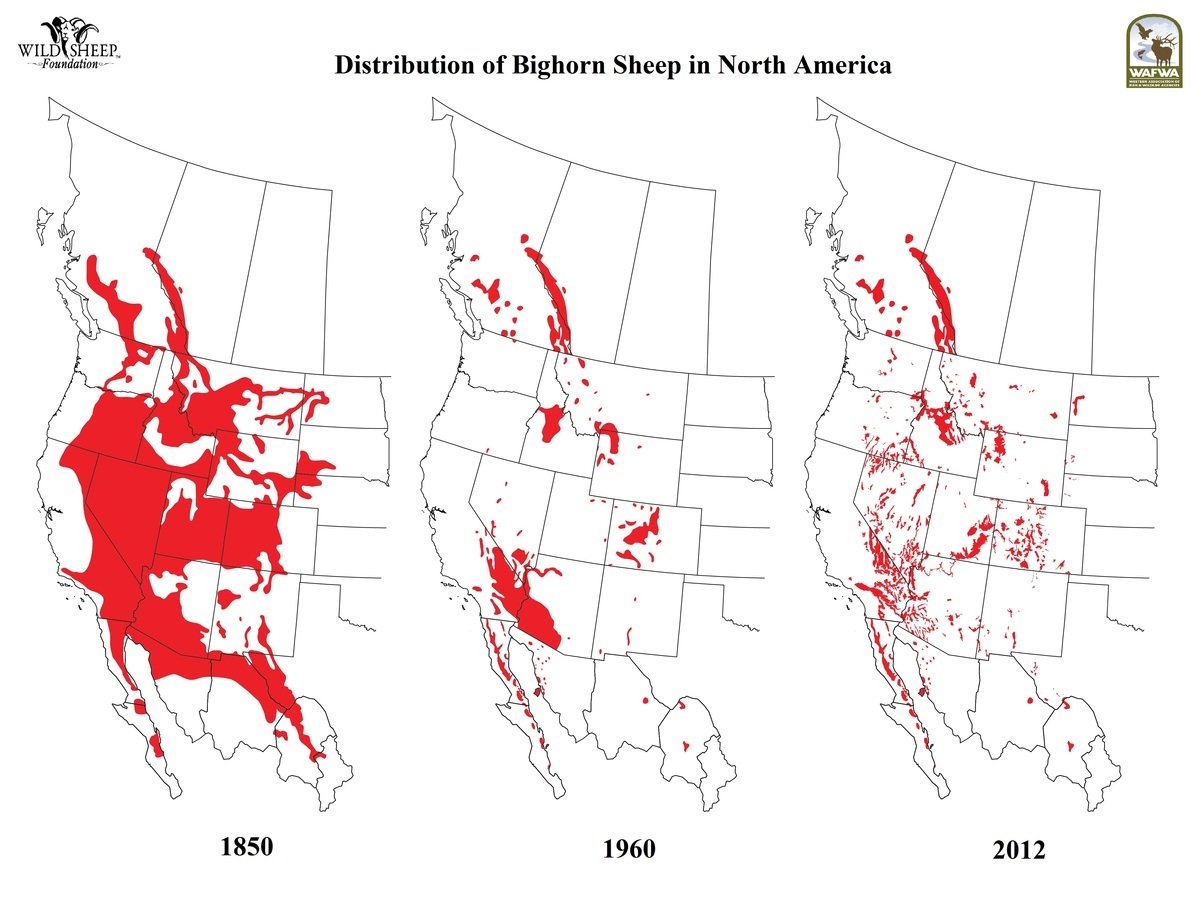
Hells Canyon

Early analyses

Some protective immunity in adults...

Plowright, Manlove et al. (2013) PLoS One

More exposure = lower risk

Raina Plowright

...but this does not transfer to lambs

Frances Cassirer

May 1

Sept 1

Daily lamb mortality hazard

Cassirer, Manlove et al. (2013) Jo Anim Ecol

0.035

0.000

Years with transmission

Years without transmission

Limited cross-stain immunity

Cassirer, Manlove et al. (in press) Jo Wildife Manage

Photo: Jo Ohm

Novel strain introduction into                                 herd

Mike Lerch

Jo Ohm

previously infected

Frances Cassirer

Observed; no symptoms

Observed with symptoms

Carriage and infectious period

Plowright, Manlove et al. (in prep)

Lostine sheep trap

Raina Plowright

"Chronic carriers"

"Resistant"

Frances Cassirer

Carriers are crucial for

pathogen persistence

Animals sampled 3 or more times

My Questions

1. How do die-offs and persistent disease compare in terms of population effects?

2. Is transmission frequency- or density-dependent?

3. Do all infected animals pose similar risks to lambs?

4. What would have made learning more efficient?

Field work

~4500 locations

(10% of full dataset)

4 states / 4 pops/ 4 years

~1130 focal follows

2013: Mike Lerch

2014: Jo Ohm

2015-2016:

Logan Weyand

1. How do die-offs and persistent disease compare?

Immediate fade-out vs. pathogen persistence

Return to original state

No return

Scheffer et al. (2001) Nature

Timeseries with phase transitions

Sahara-derived dust

Years before present

Oceanic "state"

Manlove et al. (2016) Ecology

Manlove et al. (2016) Ecology

Manlove et al. (2016) Ecology

Persistence produces a phase-transition.

Die-offs = occassional shock; no change in attractor

My Questions

1. How do die-offs and persistent disease compare in terms of population effects?

2. Is transmission frequency- or density-dependent?

3. Do all infected animals pose similar risks to lambs?

4. What would have made this easier?

Persistence = phase-transition

2. Is transmission frequency- or density-dependent?

What is the scale of transmission during lamb events?

Do number contacts change with population "density"?

Scale of transmission

Low between-group variance

High between-group variance

=> System-wide transmission

=> Local transmission

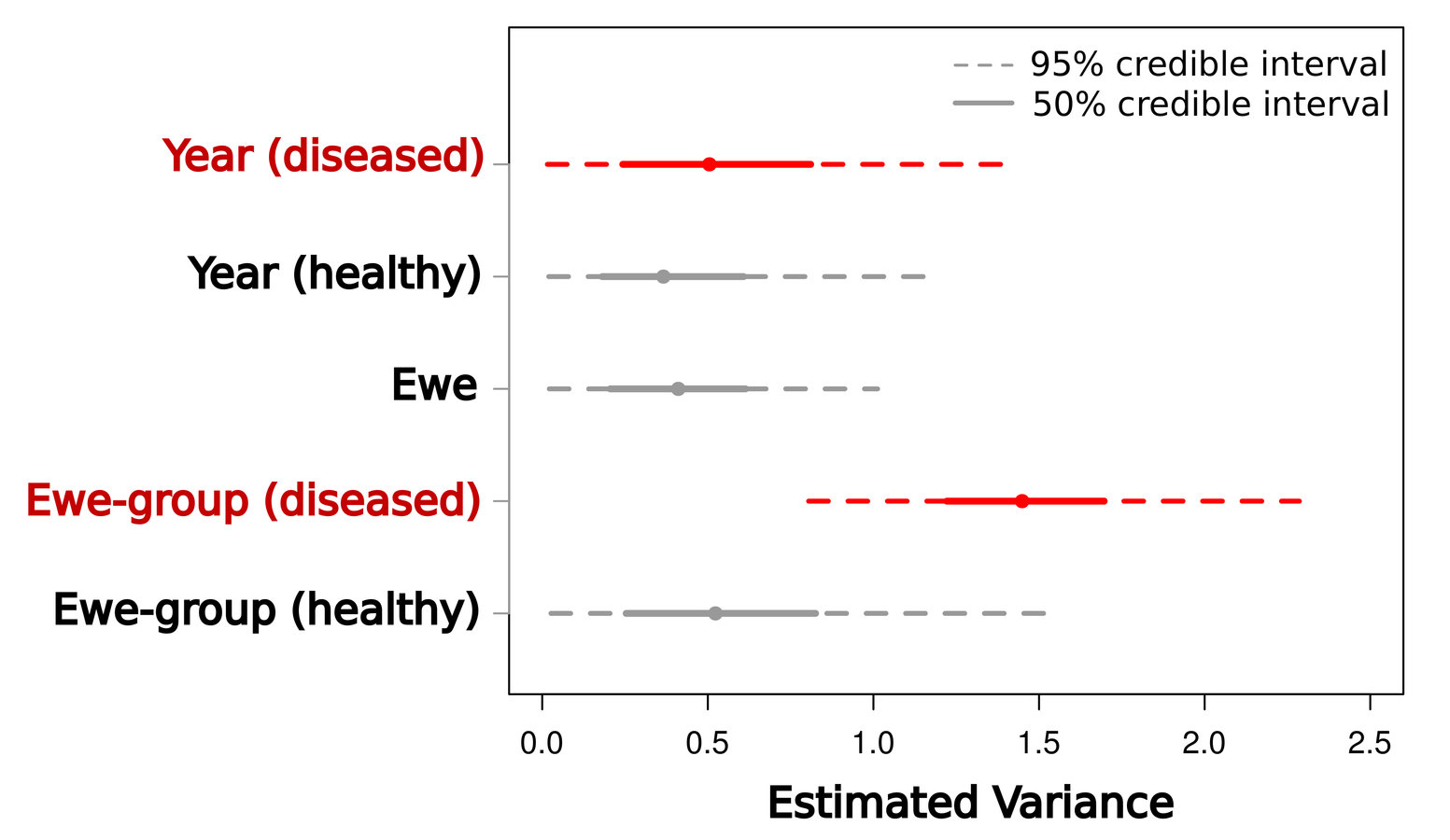
Manlove et al. (2014) Proc R Soc B

Transmission localized within ewe-groups

Group size

Manlove et al. (2014) Proc R Soc B

Contact rate doesn't scale with population size

=> Frequency-dependent transmission

Population size

My Questions

1. How do die-offs and persistent disease compare in terms of population effects?

2. Is transmission frequency- or density-dependent?

3. Do all infected animals pose similar risks to lambs?

4. What would have made this easier?

Frequency-dependent during persistence

3. Do all infected animals pose similar risks to lambs?

Who contacts who, when?

How does contact map to transmission?

P(transmission | contact)

Ewes with lambs ("dams")

Lambs

Yearlings

Yearlings are reservoirs for infection

 

logit(Movi-positive)

 

Age

Manlove et al. (in review)

Dams, yearlings, dry ewes all have similar mixing patterns.

Manlove et al. (in review)

Direct touch concentrated in lambs/dams.

Manlove et al. (in review)

+ \beta_{1} \sum X_{\text{Ewes with lambs}}
+β1∑XEwes with lambs+ \beta_{1} \sum X_{\text{Ewes with lambs}}
+ \beta_{2}\sum X_{\text{Ewes without lambs}}
+β2∑XEwes without lambs+ \beta_{2}\sum X_{\text{Ewes without lambs}}
+ \beta_{3} \sum X_{Yearlings}
+β3∑XYearlings+ \beta_{3} \sum X_{Yearlings}
logit(P(\text{Lamb survival})) =
logit(P(Lamb survival))=logit(P(\text{Lamb survival})) =
\beta_{0}
β0\beta_{0}

Yearlings are reservoirs for infection, but not transmission

My Questions

1. How do die-offs and persistent disease compare in terms of population effects?

2. Is transmission frequency- or density-dependent?

3. Do all infected animals pose similar risks to lambs?

4. What would have made this more efficient?

No. Highest transmission risk from reproductive ewes

What would have made this more efficient?

Improvement #1

Better cross-disciplinary communication.

Manlove et al. (2016) PLoS Biology

Improvement #2

Better comparative frameworks

for contact patterns

Animal movement histories have three components:

Individual identifier

Spatial coordinates

Timestamp

(I,S,T)
(I,S,T)(I,S,T)
I \in {1,...,N}
I∈1,...,NI \in {1,...,N}
S \in D_{S}
S∈DSS \in D_{S}
T \in D_{T}
T∈DTT \in D_{T}

Network constructions rely on intersections of marginalizations of

Nodes = levels of variable between which intersections are calculated

Edges = relative frequency of intersection occurrence

(I,S,T)
(I,S,T)(I,S,T)

Other metrics can proxy for social contacts if I, S, T are redundant

High mutual information in S and I

High mutual information in I, S, and T

Spatial networks = good proxies

Group networks = good proxies

Mutual information between Individual identity, space, time

Fission-fusion/

big groups

Territorial/

small home-ranges

Fission-fusion/

big groups

Territorial/

small home-ranges

Improvement #2

Better comparative frameworks

for disease structures

Can we project population epidemiology from within-host processes?

What within-host categorizations make sense for management?

S

I

R

S

I

R

C

S

I

My Questions

1. How do die-offs and persistent disease compare in terms of population effects?

2. Is transmission frequency- or density-dependent?

3. Do all infected animals pose similar risks to lambs?

4. What would have made this more efficient?

Better cross-disciplinary communication

Stronger comparative frameworks

Big messages

Persistence is extremely costly

Transmission is frequency-dependent

Transmission is likely driven by a few chronically infected dams

Need more synthesis

Thanks!

Michael Lerch

Johanna Ohm

Logan Weyand

K.C. Hill

Paul Wik

Bob Dice

Sonja Andersen

Frances

Tom

Pete

Raina

Paul

Andrew Read

Ottar Bjornstad

Ephraim Hanks

Matt Ferrari

Mary Poss

In Lewiston and Lewistown

In State College

Christina Aiello

Kurt Vandegrift

Nina Wale

Amelia McKee

Lauren Quevillon

CIDD affiliates

In Bozeman

Emily Almberg

Angela Brennan

Pauline Kamath

Bzn Disease Lab members

 

Elizabeth Fulton

Carson Butler

Bob Garrott

Penn State Academic Computing Fellows Program

Thanks!

Use

Model processes that require host interactions

Problems

Cost

Inferential limitations

How do we compare methods?

Alternative

Spatial information

Biases from partial sampling

Home range overlap networks

Spatial networks

Aggregation information (group size)

When do we need social contact networks?

Latent

Easily

Observed

Hard to observed

For some animal movement processes, easy- and hard-metrics share information.

Claim:

Predictable relationships?

Could guide network construction?

Obstacles

1. How do we quantify arrows?

2. If the relationships exist in silico, how do we test them in vivo?

Network basics

Show relationships (edges) between actors (nodes)

Metrics describe structure of relationships

Degree = How many relationships an actor has

Modularity = Extent to which relationships substructure into particular groups

Social contact networks

Nodes = individuals

Edges = in same group

Spatial networks

Nodes = locations in space (e.g., traps on a grid, waterholes, corners of a transect)

Edges = 1) spatial distance between points; 2) animals observed at both locations

Home-range overlap networks

Nodes = individuals

Edges = extent to which home-ranges overlap

Contact network constructions

A little formalism: Animal movements

Animal movement histories have three components:

Individual identifier

Spatial coordinates

Timestamp

(I,S,T)
(I,S,T)(I,S,T)
I \in {1,...,N}
I∈1,...,NI \in {1,...,N}
S \in D_{S}
S∈DSS \in D_{S}
T \in D_{T}
T∈DTT \in D_{T}

(All?) models in population biology rely on some aspect of

(I,S,T)
(I,S,T)(I,S,T)
Analysis Variable aggregated out Marginal used
Individual home-range
Population-level movements
Individual survival
f_{I,S} = \int_{t \in T}f_{(I,S,T)}dt
fI,S=∫t∈Tf(I,S,T)dtf_{I,S} = \int_{t \in T}f_{(I,S,T)}dt
f_{S,T} = \sum_{i \in I}f_{(I,S,T)}
fS,T=∑i∈If(I,S,T)f_{S,T} = \sum_{i \in I}f_{(I,S,T)}
f_{I,T} = \int_{s \in S}f_{(I,S,T)}ds
fI,T=∫s∈Sf(I,S,T)dsf_{I,T} = \int_{s \in S}f_{(I,S,T)}ds
T
TT
I
II
S
SS

Case 1: Social contact network

First claim

All network constructions rely on intersections of some marginal distribution of

(I,S,T)
(I,S,T)(I,S,T)

Nodes = levels of variable between which intersections are calculated

Edges = relative frequency of intersection occurrence

Two individuals,     and

I_{1}
I1I_{1}
I_{2}
I2I_{2}

, with movement paths                                     and

X_{1} = (I = I_{1}, S, T)
X1=(I=I1,S,T)X_{1} = (I = I_{1}, S, T)
X_{2} = (I = I_{2}, S, T)
X2=(I=I2,S,T)X_{2} = (I = I_{2}, S, T)
X_{1} \cap X_{2}
X1∩X2X_{1} \cap X_{2}

, contains all points

where      and     co-occur in

I_{1}
I1I_{1}
I_{2}
I2I_{2}
(S,T)
(S,T)(S,T)

(aka their "contacts")

Case 2: Spatial networks

Two sites,     and

S_{1}
S1S_{1}

, with visit histories                                      and

X_{S1} = (I, S = S_{1}, T)
XS1=(I,S=S1,T)X_{S1} = (I, S = S_{1}, T)
X_{S2} = (I, S = S_{2}, T)
XS2=(I,S=S2,T)X_{S2} = (I, S = S_{2}, T)
X_{S1} \cap X_{S2}
XS1∩XS2X_{S1} \cap X_{S2}

The set of path intersections,

is empty.

S_{2}
S2S_{2}

BUT, not empty if we aggregate over (= marginalize out) time

X_{S1} = (I, S = S_{1})
XS1=(I,S=S1)X_{S1} = (I, S = S_{1})
X_{S2} = (I, S = S_{2})
XS2=(I,S=S2)X_{S2} = (I, S = S_{2})

and

X_{S1} \cap X_{S2}
XS1∩XS2X_{S1} \cap X_{S2}

= frequency with which      and      share animals

S_{1}
S1S_{1}
S_{2}
S2S_{2}

Forward

Why sheep?

What else?

Model for how to learn about an EID with limited, realistic data.

Luke Manlove

Almberg, Manlove et al. in prep

S

E

I

C

R

birth

\lambda
λ\lambda

3 weeks

16 weeks

lifelong

lifelong

Emily Almberg

Main findings

3. Yearlings were disproportionately infected, but appeared to rarely transmit

1. Yearlings, dry ewes, and dams all had similar group-level association patterns

2. Direct touch was concentrated around lambs, and dams with lambs

While yearlings may be a reservoir for infection, they are not a reservoir for transmission

Main Findings

1. Disease introduction is associated with a long-term shift in bighorn population dynamics.

2. Phase-transition is driven by disease-induced mortality in lambs.

3. Persistence rapidly overtakes all-age die-offs as major driver of pop. dynamics

"One Health" or Three?

Is disease modeling becoming more cross-disciplinary?

Manlove et al. (2016) PLoS Biology

Motivating question:

Manlove et al. (2016) PLoS Biology

Manlove et al. (2016) PLoS Biology

Manlove et al. (2016) PLoS Biology

Manlove et al. (2016) PLoS Biology

Main points

1. Lamb pneumonia transmission is localized into ewe groups

2. As populations get larger, more groups appear, but group size remains relatively constant

...so, number of infectious contacts probably doesn't scale with density.

Pathogen could drive host extinct.

Objectives

1. Document long-term population dynamics in Hells Canyon following die-off events

2. Estimate vital rates in the presence and absence of disease

3. Compare demographic costs of all-age die-offs vs. persistent lamb disease

Why does population structure matter?

If transmission scales with population density, disease can't drive host extinct.

Question

How does lamb pneumonia transmission relate to density?

Field methods

Associations

- located marked animals every 1-3 days

- group membership, lamb and health status, group size and composition

Interactions

- ~1600 10-minute group focal follows

- identity, duration, form of direct contacts

Scope

- 3 populations

- 3 summers

- 60% of adults/yearlings marked

A framework relating network constructions

Motivating question

Was it necessary to find all those animals every day?

When are spatial networks good proxies for social contacts?

Network basics

Show relationships (edges) between actors (nodes)

Metrics describe structure of relationships

Degree = How many relationships an actor has

Modularity = Extent to which relationships substructure into particular groups

Social contact networks

Nodes = individuals

Edges = in same group

Spatial networks

Nodes = locations in space (e.g., traps on a grid, waterholes, corners of a transect)

Edges = 1) spatial distance between points; 2) animals observed at both locations

Home-range overlap networks

Nodes = individuals

Edges = extent to which home-ranges overlap

Contact network constructions

Disease ecologists use both spatial and social networks

No clear framework for how spatial and social networks relate to one another

Decision-making process remains ad hoc

Spatial

Social

Gerbils

Prairie dogs

Cholera in humans

"Fission-fusion" societies

Lions

Tasmanian devils

When are spatial networks good proxies of social contacts?

A little formalism: Animal movements

Animal movement histories have three components:

Individual identifier

Spatial coordinates

Timestamp

(I,S,T)
(I,S,T)(I,S,T)
I \in {1,...,N}
I∈1,...,NI \in {1,...,N}
S \in D_{S}
S∈DSS \in D_{S}
T \in D_{T}
T∈DTT \in D_{T}

(All?) models in population biology rely on some aspect of

(I,S,T)
(I,S,T)(I,S,T)
Analysis Variable aggregated out Marginal used
Individual home-range
Population-level movements
Individual survival
f_{I,S} = \int_{t \in T}f_{(I,S,T)}dt
fI,S=∫t∈Tf(I,S,T)dtf_{I,S} = \int_{t \in T}f_{(I,S,T)}dt
f_{S,T} = \sum_{i \in I}f_{(I,S,T)}
fS,T=∑i∈If(I,S,T)f_{S,T} = \sum_{i \in I}f_{(I,S,T)}
f_{I,T} = \int_{s \in S}f_{(I,S,T)}ds
fI,T=∫s∈Sf(I,S,T)dsf_{I,T} = \int_{s \in S}f_{(I,S,T)}ds
T
TT
I
II
S
SS

Case 1: Social contact network

First claim

All network constructions rely on intersections of some marginal distribution of

(I,S,T)
(I,S,T)(I,S,T)

Nodes = levels of variable between which intersections are calculated

Edges = relative frequency of intersection occurrence

Two individuals,     and

I_{1}
I1I_{1}
I_{2}
I2I_{2}

, with movement paths                                     and

X_{1} = (I = I_{1}, S, T)
X1=(I=I1,S,T)X_{1} = (I = I_{1}, S, T)
X_{2} = (I = I_{2}, S, T)
X2=(I=I2,S,T)X_{2} = (I = I_{2}, S, T)
X_{1} \cap X_{2}
X1∩X2X_{1} \cap X_{2}

, contains all points

where      and     co-occur in

I_{1}
I1I_{1}
I_{2}
I2I_{2}
(S,T)
(S,T)(S,T)

(aka their "contacts")

Case 2: Spatial networks

Two sites,     and

S_{1}
S1S_{1}

, with visit histories                                      and

X_{S1} = (I, S = S_{1}, T)
XS1=(I,S=S1,T)X_{S1} = (I, S = S_{1}, T)
X_{S2} = (I, S = S_{2}, T)
XS2=(I,S=S2,T)X_{S2} = (I, S = S_{2}, T)
X_{S1} \cap X_{S2}
XS1∩XS2X_{S1} \cap X_{S2}

The set of path intersections,

is empty.

S_{2}
S2S_{2}

BUT, not empty if we aggregate over (= marginalize out) time

X_{S1} = (I, S = S_{1})
XS1=(I,S=S1)X_{S1} = (I, S = S_{1})
X_{S2} = (I, S = S_{2})
XS2=(I,S=S2)X_{S2} = (I, S = S_{2})

and

X_{S1} \cap X_{S2}
XS1∩XS2X_{S1} \cap X_{S2}

= frequency with which      and      share animals

S_{1}
S1S_{1}
S_{2}
S2S_{2}

Second claim

Network constructions can proxy for one another under appropriate correlations of

I, S, \text{ and } T
I,S, and TI, S, \text{ and } T

First claim

All network constructions rely on intersections on some marginal distribution of

(I,S,T)
(I,S,T)(I,S,T)

Nodes = levels of variable between which intersections are calculated

Edges = relative frequency of intersection occurrence

Third claim

Correlations in                         can be predicted from animal behaviors

I, S, \text{ and } T
I,S, and TI, S, \text{ and } T

Do these claims hold (in silico, or in vivo)?

In silico

Simulated movement trajectories for

    N = 50 animals over

    T = 100 timesteps on an

    S = 10x10 grid

Three governing movement parameters (varied systematically on log-scale)

              Social affinity (desire to stay with current associates)

              Spatial affinity (desire to stay within a particular territory)

              Habitat heterogeneity (desirability of particular sites for all animals)

Recorded

      Social contact network metrics (degree, modularity, transitivity, average distance)

      Spatial network metrics (using animal-visits-multiple-sites as edges)

      Home-range and defensibility (= day-range:home-range)

      Group size distributions (fit with a Poisson model; summarize with    )

\lambda
λ\lambda
\gamma =
γ=\gamma =
\delta =
δ=\delta =
\rho =
ρ=\rho =

In vivo

Do group size and defensibility vary systematically with one another?

Have network studies used construction methods that vary with group size/defensibility?

Main points

Network constructions have consistent probabilistic relationships that we don't formally use.

In some cases, spatial networks are good proxies for social networks

  • Matriarchal societies with stable group membership

In some cases, social networks can be collapsed to groups

  • Territorial species living on well-defined home-ranges

Theory needs calibration and validation on the ground

Acknowledgements

Made with Slides.com