DBAC: Double-bracket Algorithmic Cooling

  1. About me
  2. Double-bracket Quantum Imaginary Time Evolution (QITE)
  3. DBAC Compilation for single qubit
  4. Quantum Dynamic Programming

Kay Giang - NTU

slides.com/khanhuyengiang

Master and Bachelor at University of Oxford

  • Thesis was in Astrophysics
  • Coursework in Quantum Information

Research Assiant at Nanyang Technological University in Singapore

  • Multidisciplinary projects - theory, numeric and experimental
  • DB-RESET: Algorithmic cooling using double-bracket

About me

Khanh Uyen (Kay) Giang

Outside physics, I enjoy watercolor art, pottery and ice-skating

Double-bracket Quantum Imaginary Time Evolution

(DB-QITE)

Gluza et al., arxiv:2412.04554

QITE formula

|\Psi(\tau)\rangle = \frac{e^{-\tau \hat{H}}}{\|e^{-\tau \hat{H}}|\Psi(0)\rangle\|} |\Psi(0)\rangle

\(\Psi(0)\): Initial state

\(\Psi(\tau)\): State at time \(\tau\)

\(\hat H\): Diagonalised Hamiltonian

Cool the initial state \(\Psi(0)\) with respect to the Hamiltonian \(\hat H\)

DB-QITE formula

|\Psi(\tau)\rangle = \frac{e^{-\tau \hat{H}}}{\|e^{-\tau \hat{H}}|\Psi(0)\rangle\|} |\Psi(0)\rangle

Gluza et al. (2412.04554) shows that QITE satisfy:

\begin{align*} \partial_\tau {|\Psi(\tau) \rangle} = [\Psi(\tau),\hat{H}] |\Psi(\tau) \rangle \end{align*}

Double-bracket

\frac{\partial \Psi(\tau)}{\partial \tau} = \big[ [\Psi(\tau),\hat H],\Psi(\tau)\big]

In terms of the density matrix \(\Psi(\tau)\):

Recursion step

\ket{\Psi(t)}\approx e^{t[\Psi(0),\hat H]}\ket{\Psi_0}

For short duration t:

\partial_\tau {|\Psi(\tau) \rangle} = [\Psi(\tau),\hat{H}] |\Psi(\tau) \rangle\

This motivates defining the recursion step:

\ket{\psi_{k+1}} = e^{t_k[\psi_k,\hat H]} \ket{\psi_k}

\(\ket{\psi_k}\): State at step \(k\) 

DB-QITE recursion formula

\ket{\psi_{k+1}} = e^{t_k[\psi_k,\hat H]} \ket{\psi_k}
\boxed{\ket{\psi_{k+1}} \approx e^{i\sqrt{t_k}\hat H} e^{i\sqrt{t_k}\psi_k} e^{-i\sqrt{t_k}\hat H}\ket{\psi_k}}
e^{t[\psi,\hat H]} = e^{i\sqrt{t}\hat H}e^{i\sqrt{t}\psi} e^{-i\sqrt{t}\hat H} e^{-i\sqrt{t}\psi} + \mathcal O(t^{3/2})

Using the group commutator relation:

DB-QITE recursion formula:

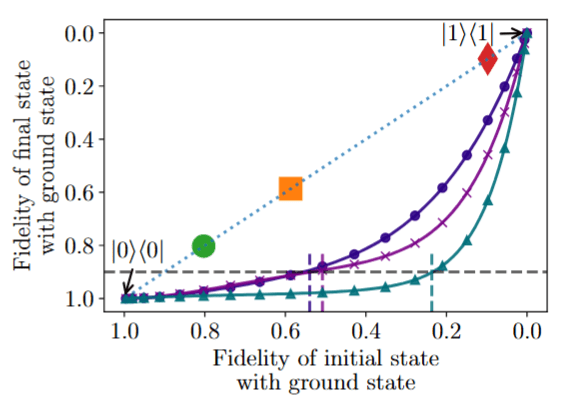
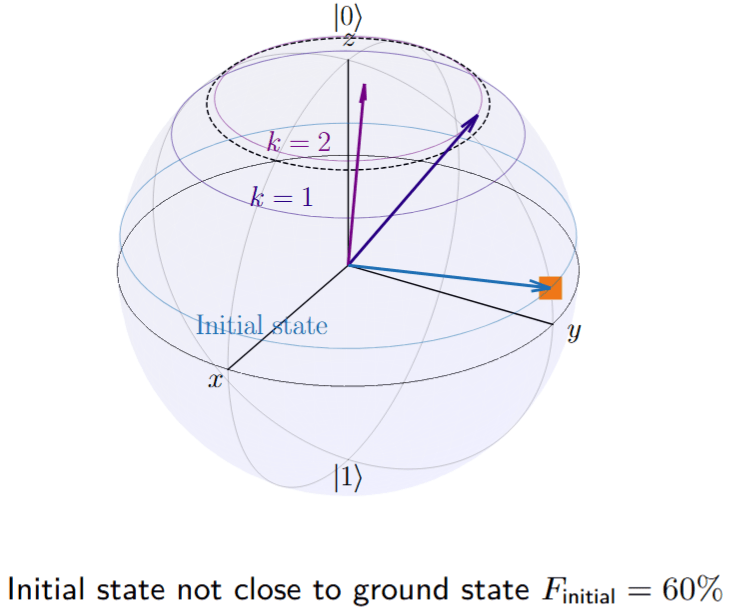
Fidelity increase guarantee

\boxed{\ket{\psi_{k+1}} \approx e^{i\sqrt{t_k}\hat H} e^{i\sqrt{t_k}\psi_k} e^{-i\sqrt{t_k}\hat H}\ket{\psi_k}}
F_{k+1} \geq 1- (1- t F_0 \Delta)^{k}

Fidelity with ground state after step \(k+1\):

\(F_0\): fidelity between the initial state with ground state

\(\Delta\): spectral gap

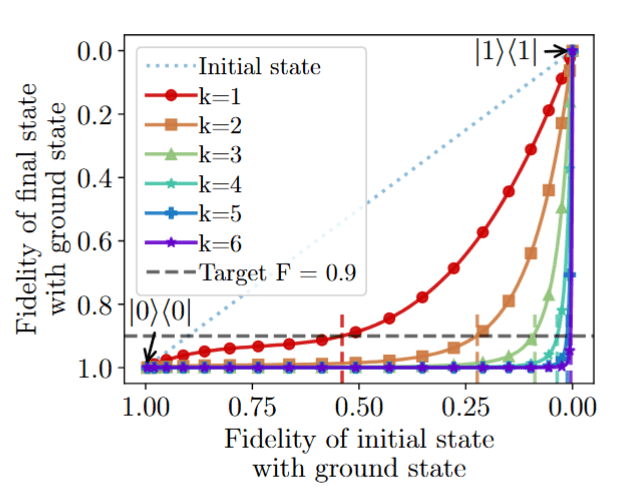
DB-QITE Performance

\boxed{\ket{\psi_{k+1}} \approx e^{i\sqrt{t_k}\hat H} e^{i\sqrt{t_k}\psi_k} e^{-i\sqrt{t_k}\hat H}\ket{\psi_k}}

If we have ideal \(e^{i\sqrt{t_k}\psi_k}\)

DBAC compilation for single qubit case

Compilation for resetting one qubit

\boxed{\ket{\psi_{k+1}} \approx e^{i\sqrt{t_k}\hat H} e^{i\sqrt{t_k}\psi_k} e^{-i\sqrt{t_k}\hat H}\ket{\psi_k}}

\(e^{i\sqrt{t_k}\psi_k}\): Density matrix exponentiation (DME)

Single qubit: \(\hat H = \hat Z\)

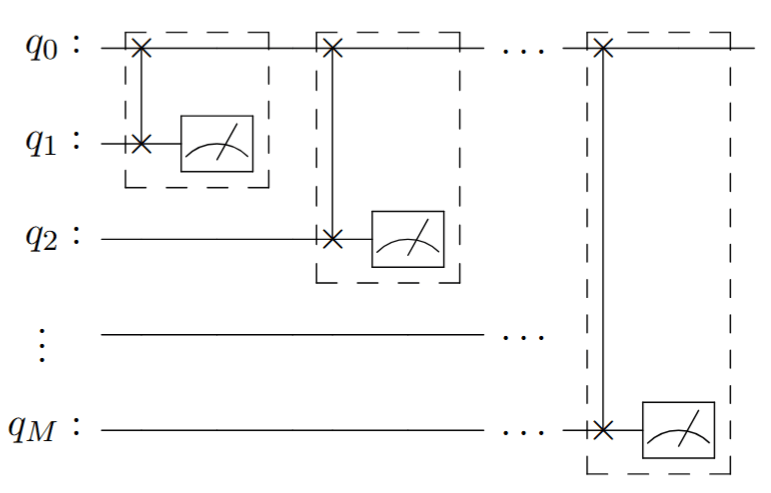
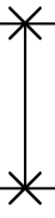
: \(\delta\)SWAP gate, applying \(e^{-i t \text{SWAP}}\). Compiled using Heisenberg interaction: \(e^{it(XX+YY+ZZ)}\)

DME Circuit

\boxed{\ket{\psi_{k+1}} \approx e^{i\sqrt{t_k}\hat H} e^{i\sqrt{t_k}\psi_k} e^{-i\sqrt{t_k}\hat H}\ket{\psi_k}}
\begin{align*} \hat{E}_t^{(\rho)}(\sigma) &= \text{Tr}_{1}\left[e^{-i t \text{SWAP}}(\rho\otimes\sigma) e^{i t \text{SWAP}}\right]\\ &= \sigma - it[\rho,\sigma] +O(t^2)\\ &= e^{-it\rho} \sigma e^{it\rho} +O(t^2) \end{align*}

Density matrix exponentiation

The DME channel is:

Repeating \(M\) iterations yields:

\left(\hat{E}_{(t/M)}^{(\rho)}(\sigma)\right)^{M} = e^{-it\rho} \sigma e^{it\rho} + O(t^2/M)

DME Circuit

  • This DME protocol was introduced in Kjaergaard et al., arxiv:2001.08838
  • In their paper, they use the 3 CNOT decompositions for the \(\delta\text{SWAP}\) gate, and performed it on only 2 qubits
  • No literature has performed DME on more qubits

DME Circuit

\(\delta\)SWAP compiled using Heisenberg interaction: \(e^{it(XX+YY+ZZ)}\)

Reason for using ZZ interaction: The entangling operation in transmon qubit is Stark-induced ZZ by level excursions (siZZle)

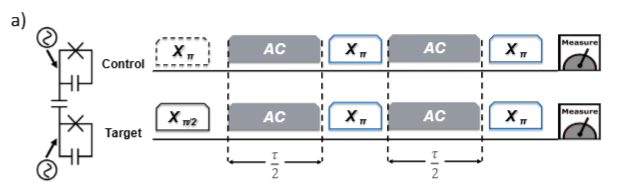
Example DBAC Circuits

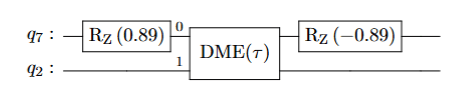
\(k=1\) recursion step (with optimized \(t_k\)):

\(k=2\) recursion steps:

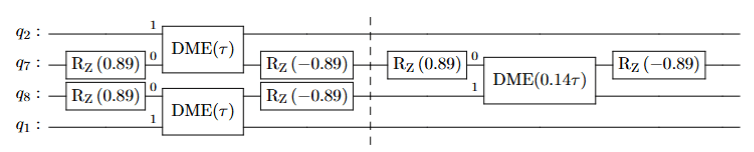
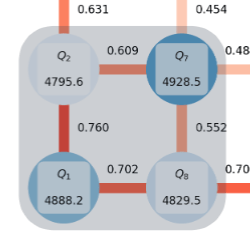
\boxed{\ket{\psi_{k+1}} \approx e^{i\sqrt{t_k}\hat H} e^{i\sqrt{t_k}\psi_k} e^{-i\sqrt{t_k}\hat H}\ket{\psi_k}}

DBAC Performance

\(k=2\) recursion steps (3 copies of the reset qubit):

Qubit chip layout

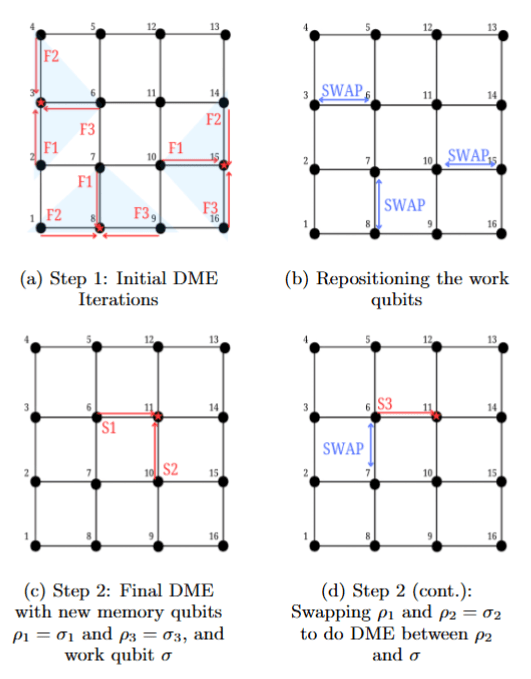
Comparing DBAC with existing protocols

HBAC

  1. Work iteratively
  2. NMR/ solid state that have a thermal bath
  3. Work on any state
  4. Cool an ensemble of qubit
  5. Complex unitary decomposition
  6. Using a full SWAP operation

DBAC

  1. Work iteratively
  2. Superconducting system, does not use a bath
  3. Only work on pure states
  4. Cool one qubit
  5. Simple decomposition
  6. Partial SWAP using hardware-natural decomposition \(\to\) faster

Heat bath algorithmic cooling

Microwave drive

  • High fidelity (99.5-99.8%)
  • Duration: 500ns
  • Hardware specific
  • Lower fidelity
  • Duration: ~200ns for 1 step
  • General purpose

DBAC

Why DBAC?

  • Enable qubit chip testing with clear interpretable results and exponential complexity
  • Dynamic nature, allows repetition on varied qubit layout
  • Proof of principle for a new class of algorithm: dynamic quantum algorithm

Quantum Dynamic Programming (QDP)

A framework that uses copies of the recursive state to implement the recursion step unitary

Static vs Dynamic

  • Usual quantum computing is static: To change operation, we have to change the circuit
  • Dynamic quantum computing: To change operation, only need to change instruction qubit

Normal way we do quantum computing: Static

Dynamic Quantum Computing

Kjaergaard et al., arxiv:2001.08838

Dynamic Quantum Algorithm

  • Question 1: Can quantum information be the source code?
  • Answer: Kimmel et al. (arxiv 1608.00281) shows that this model is basis of a universal model for quantum computation

Dynamic Quantum Algorithm

  • Questions 2: What would QDP be good for?
  • Example: 
    • DB-RESET
    • Provide a universal circuit that compute the Schmidt spectrum
    • For well-behaved recursions, QDP yields accurate results with polynomial depth

Quantum Dynamic Programming

  • QDP speed up recursion of the form (single memory call):
    \[ U^{(\mathcal{N},\rho)} =  V_2e^{i\mathcal{N}(\rho)}V_1\] where \(\mathcal{N}\) is any Hermitian-preserving map
  • Memory call: Idealized transformation we want to make. It asks for memory (instruction state \(\rho\)).
  • General case:

     
  • Problem: We can't implement this naturally in qunatum mechanics

Quantum Dynamic Programming

  • Solution: QDP approximate this memory call unitary:

     
  • QDP does this by using memory usage query:


    where \(N\) is the operator of the memory usage query, the partial transpose of the Choi matrix corresponding to \(\mathcal{N}\)
    • Consume (trace out) an instruction state
  • Repeat this procedure M times, we obtain
\mathcal{E}_s^{(N,\rho)}(\sigma) = Tr_\rho [e^{-iNs} (\rho\otimes\sigma) e^{iNs}]
E^{(\mathcal{N},\rho)}(\sigma) = e^{i\mathcal{N}(\rho)} \sigma e^{-i\mathcal{N}(\rho)}
\mathcal{E}^{(\mathcal{N},\rho,M)}_{QDP} \coloneqq (\mathcal{E}^{(\mathcal{N},\rho)}_{1/M})^M = E^{(\mathcal{N},\rho)} + O(1/M)

Quantum Dynamic Programming

Example: Density Matrix Exponentiation

  • Memory call unitary:                                                            
    \[E^{(\mathcal{N},\rho)}(\sigma) = e^{i\rho\theta} \sigma e^{-i\rho\theta}\]
  • Memory call operator: \[\mathcal{N}\rho = \rho \to \mathcal{N} = id\]
  • Memory usage query operator: \[N = \delta SWAP\]
  • Memory usage query: \[\sigma\to\text{Tr}_\rho[e^{-i\text{SWAP}\delta}(\sigma\otimes\rho) e^{i\text{SWAP}\delta}]\]

Quantum Dynamic Programming

Example: Oblivious Schmidt decomposition

  • Bipartite pure state \(|\psi\rangle\) has a Schmidt decomposition: 
|\psi\rangle_{AB} = \sum_j \sqrt{\lambda_j} |\phi_j\rangle_A|\chi_j\rangle_B
  • Double bracket iteration of OSD: 
e^{i\mathcal{N}(\psi_n)} = e^{s_n[D,\rho_n^{(A)}]}\otimes \mathbb{I}_B
  • Memory usage query:
  • Memory usage query operator:

Summary

  1. DB-QITE: formulate a recursion relation that implement imaginary time evolution
  2. DBAC: synthesizes a circuit that reset 1 qubit iteratively
  3. Quantum dynamic programming (QDP): uses copies of the instruction state to implement the operation

Thank you for listening!

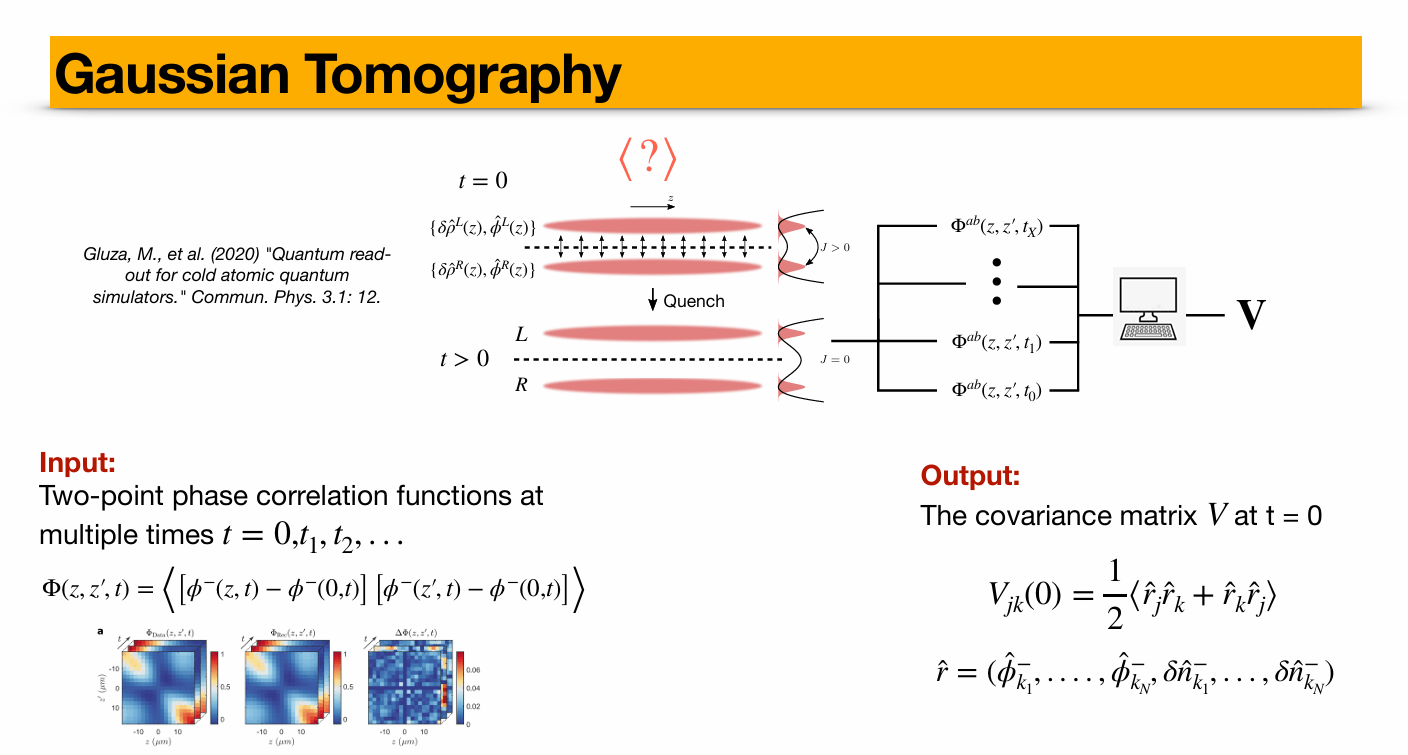
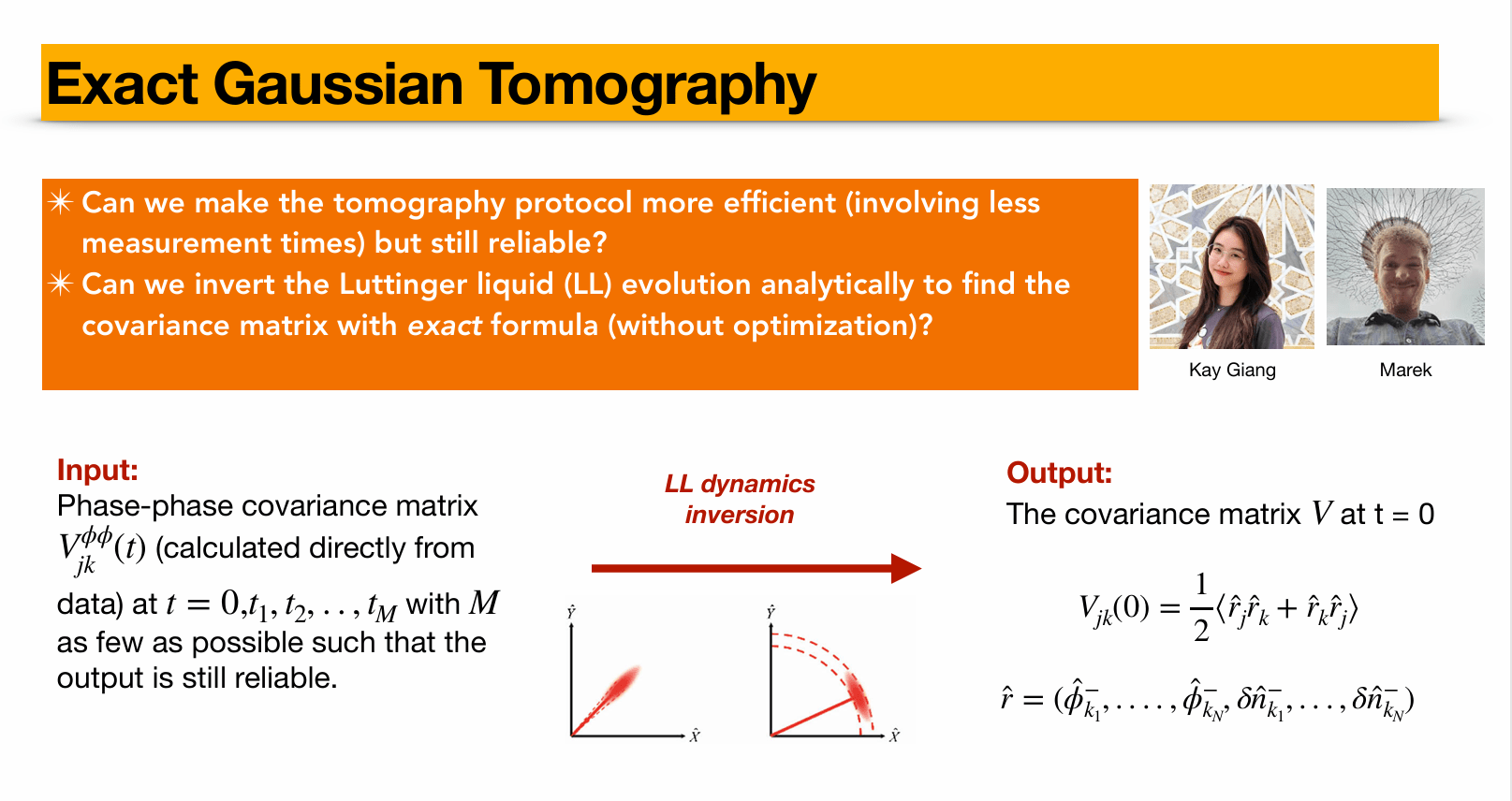
Expanding the landscape of 1D Bose gas experiment

Full exact Gaussian Tomography

Made with Slides.com