Optimizing
Gradient Descent
Kian Paimani
Zakarias Nordfäldt-Laws
May 2018
PERFORMANCE ENGINEERING
Gradient Descent - Logistic Regression
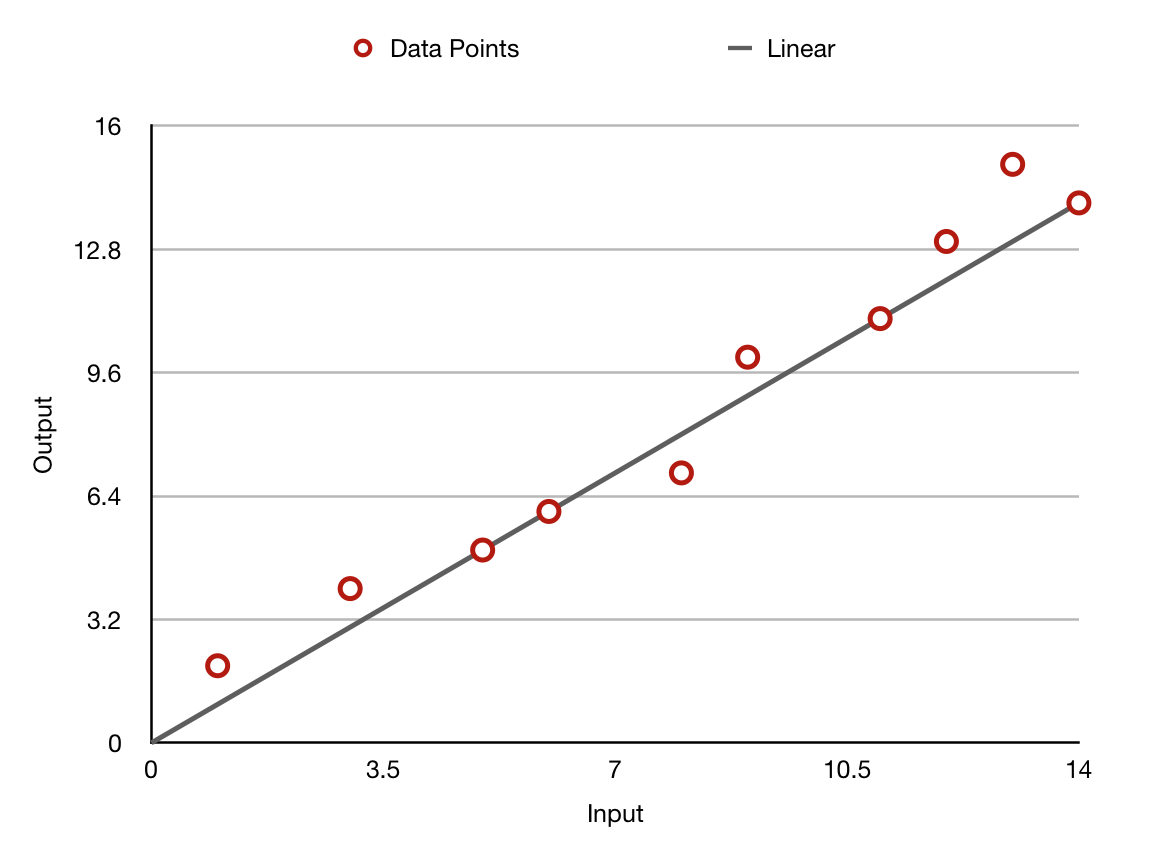
Learning Rate
Gradient Descent
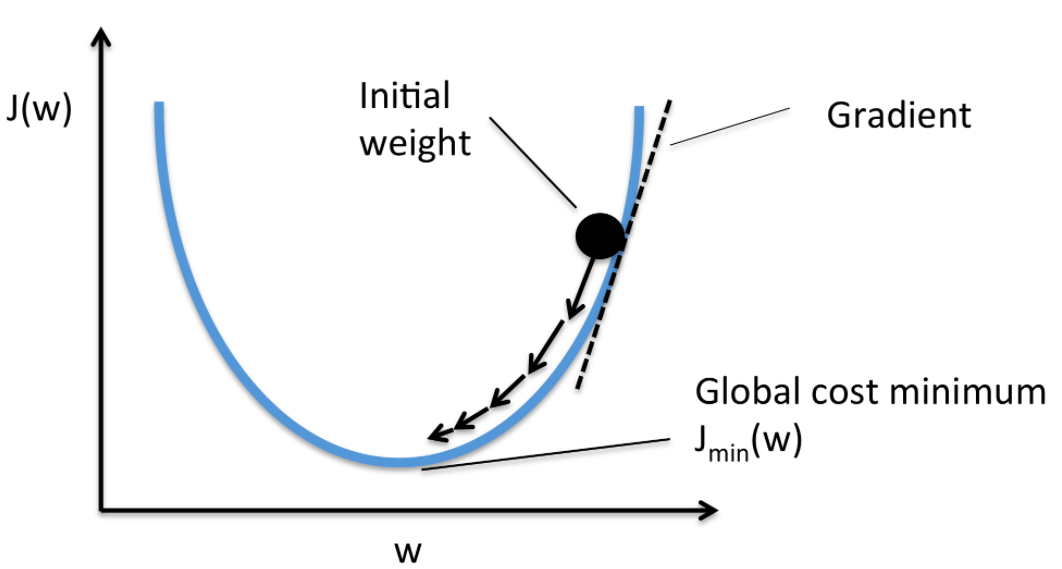
J(\theta) = \displaystyle\frac{1}{m}\sum_{t=1}^{m}(h_\theta(x^{(i)}) - y^{(i)})^2
Gradient Descent -> ADAM
- Problems
- Overshooting
- Undershooting
- Dilemmas
- Size of Dataset
- Optimized Gradient Descent: ADAM
- Momentum, Adaptive Learning Rate, Batching
Gradient Descent Applications
- Backbone of most Deep Learning Algorithms
- Deep Learning -> Tons of training data
- Must be used at very large scale to obtain accurate models.
- Iterative
- Need to observe the entire data numerous times.
Reference Implementation
for (i=1; i<iterations+1; i++){
for(z=0; z<length; z+=batch_size) {
update_gradient_batch(/* ... */);
for (n = 0; n < dim; n++) {
/* Eventually, update the weight */
par->weights[n] += (alpha * m_hat) / (sqrt(r_hat) + eps);
}
}
}void update_gradients_batch(){
for(i=start; i<start+batch_size; i++){
for (n=0; n<dim; n++) {
/* 1. Make a prediction */
/* 2. Compute error */
/* 3. Calculate gradient using the cost function */
}
}
}Analytical Model
T_{exec} = Iter_{gradient} * Gradient\_Update \bigg[ (\#_{compute} * T_{compute}) + (\#_{mem} * T_{mem}) \bigg]
+ Iter_{weight} * Weight\_Update \bigg[ (\#_{compute} * T_{compute}) + (\#_{mem} * T_{mem}) \bigg]
+ T_{overhead}
Iter_{gradient} = (iteration*\frac{data\_points}{batch\_size})
Iter_{weight} = (iteration*\frac{data\_points}{batch\_size}*dim)
Analytical Model
Iter_{gradient} = (iteration*\frac{data\_points}{batch\_size})
Iter_{weight} = (iteration*\frac{data\_points}{batch\_size}*dim)
-
Bottleneck:
- Parallelize the loop over the datapoints
-
Weight_Update is more compute heavy
- Candidate for code optimizations
- But it happens less times... 🤔
-
Tradeoff in choosing batch_size
- Large: less weight update
- Small: more weight update
datapoints >> iterations >> dim
Analytical Model
Iteration over all data
Setup
Finalize
Gradient\_Update
Weight\_Update
Gradient\_Update
Weight\_Update
Gradient\_Update
Weight\_Update
Small Batch_size
Large Batch_size
Analytical Model
Analytical Model
Analytical Model
- In Conclusion...
- The number of data points is the most important factor for operations counters.
- Increasing the batch_size reduces the weight_update phases
- but it also reduces the accuracy
- batch_size = dataset ? no!
