Digital audio primer
-
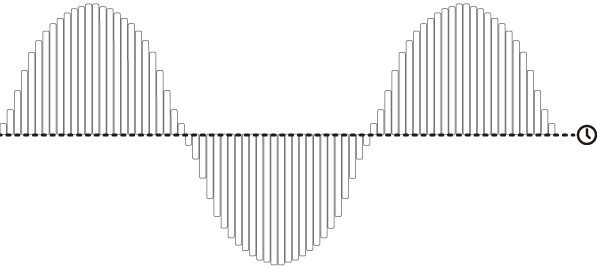
digital vs analogue
-
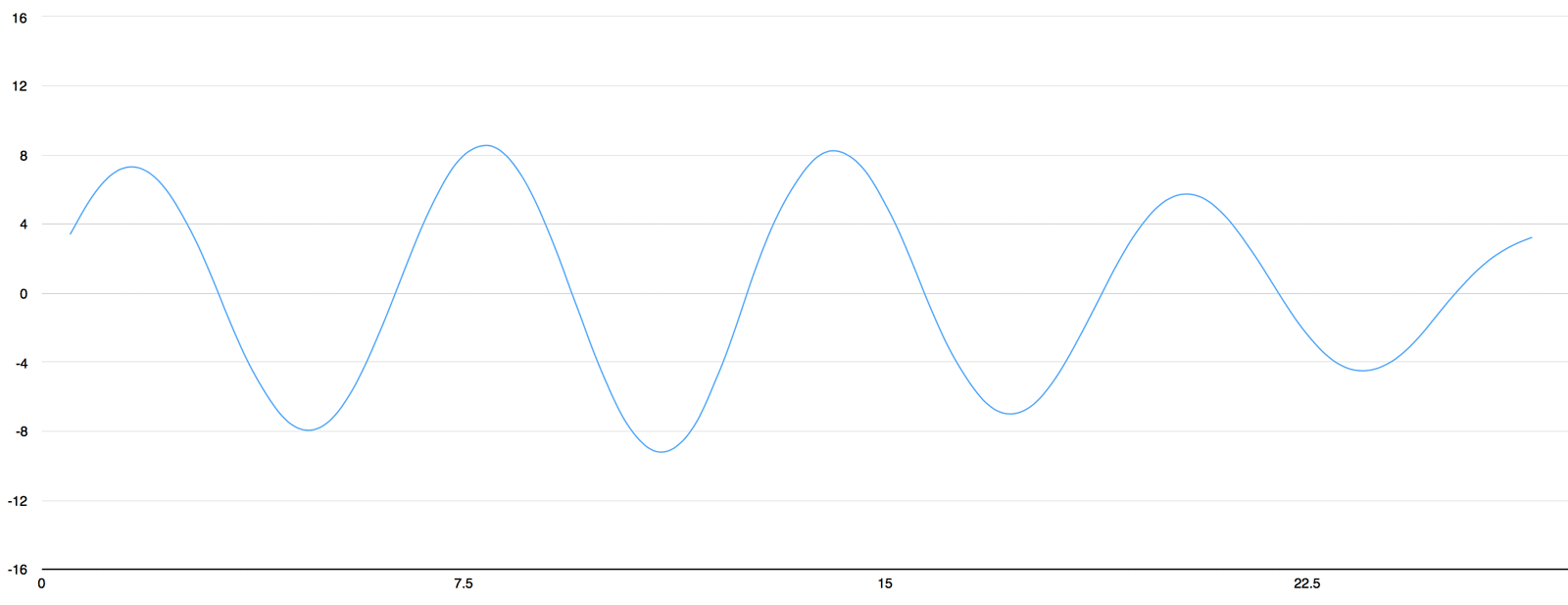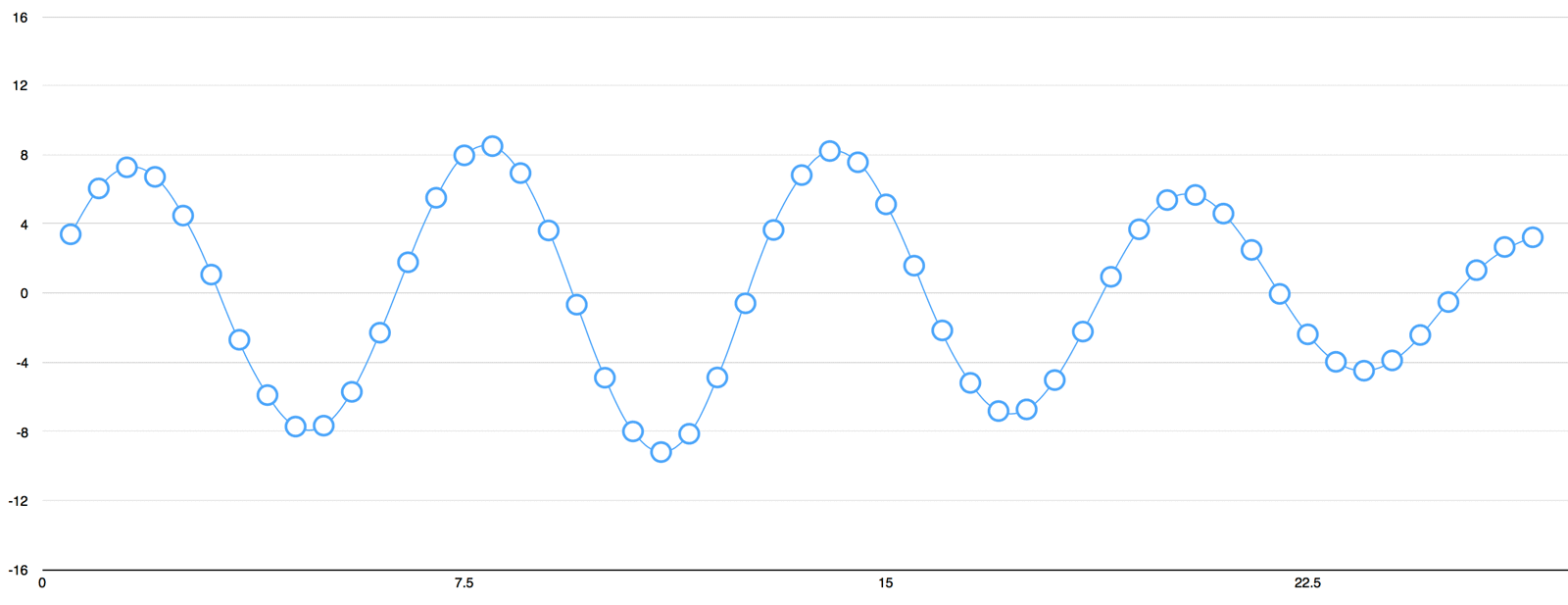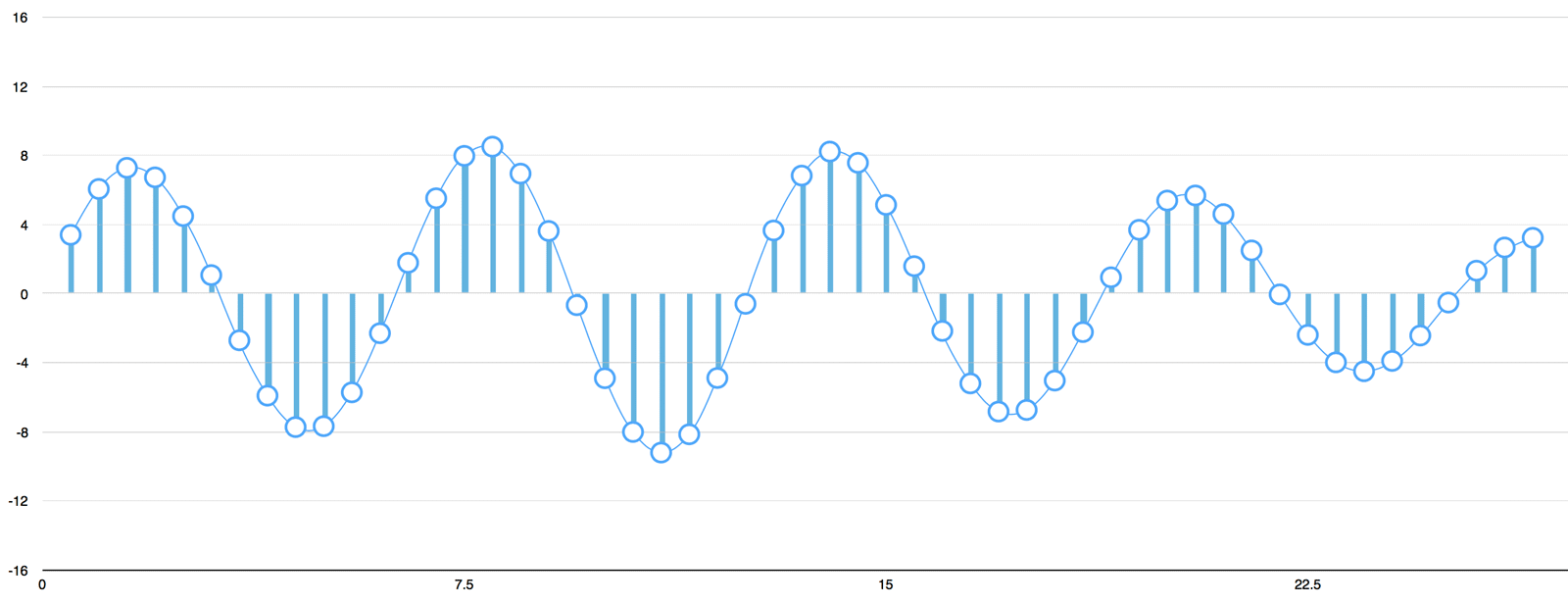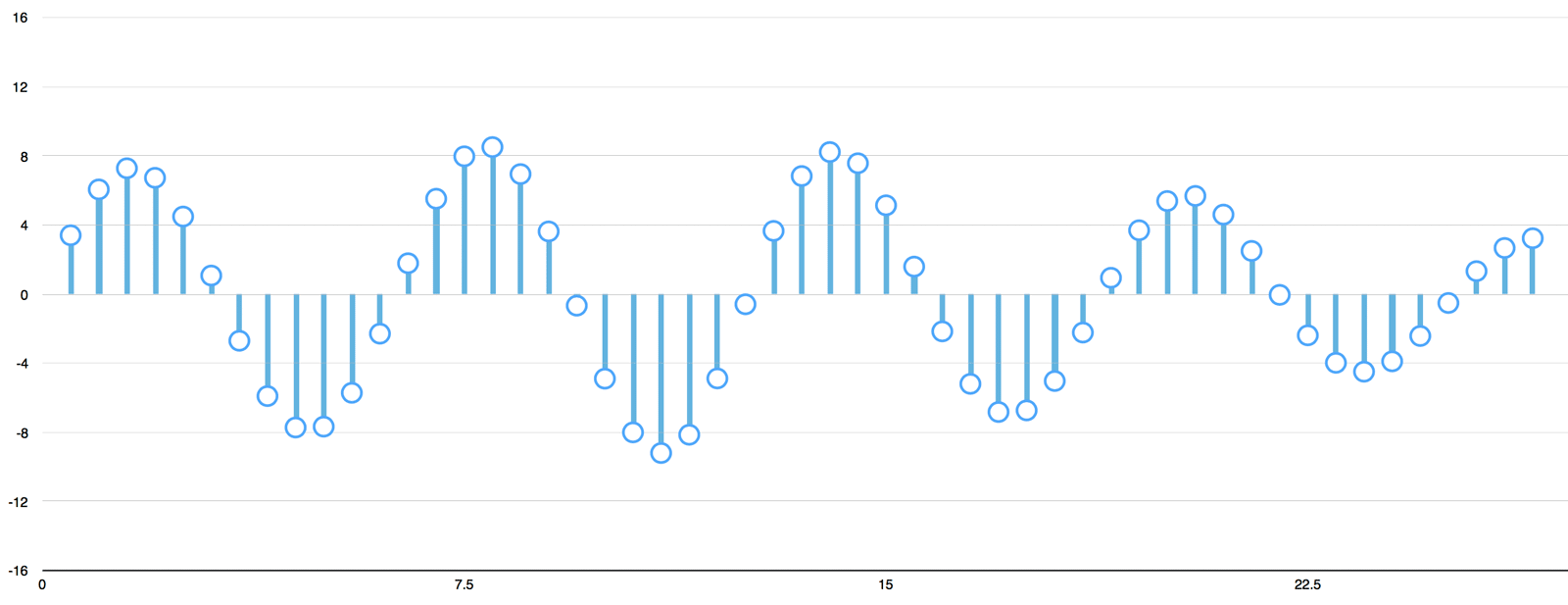
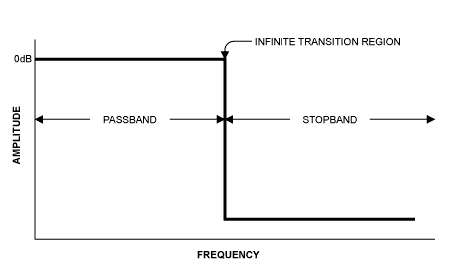
sampling theorem
-
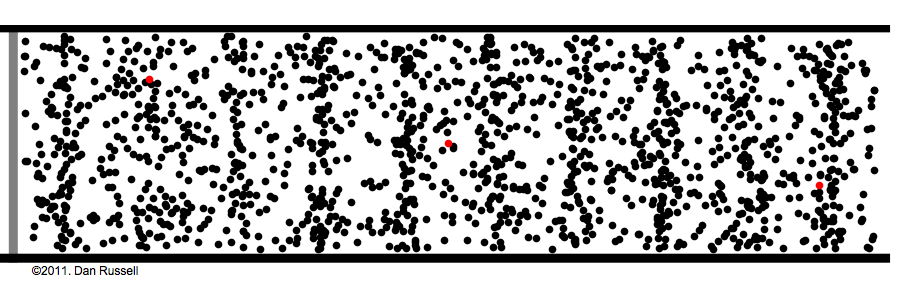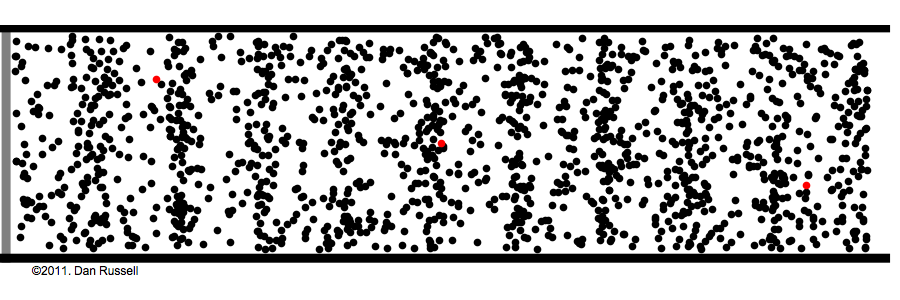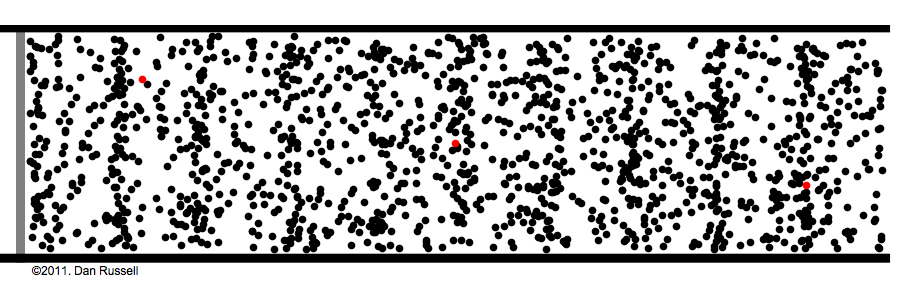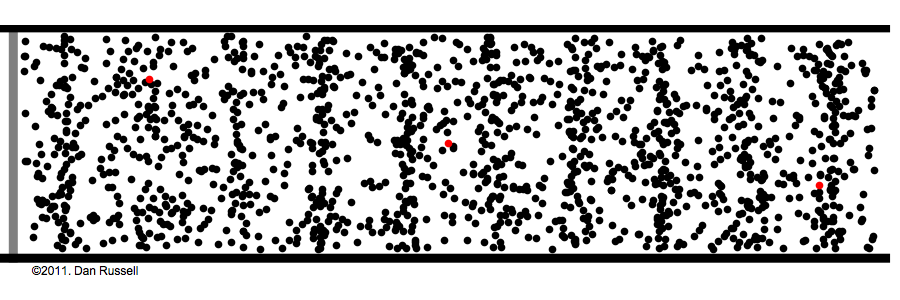
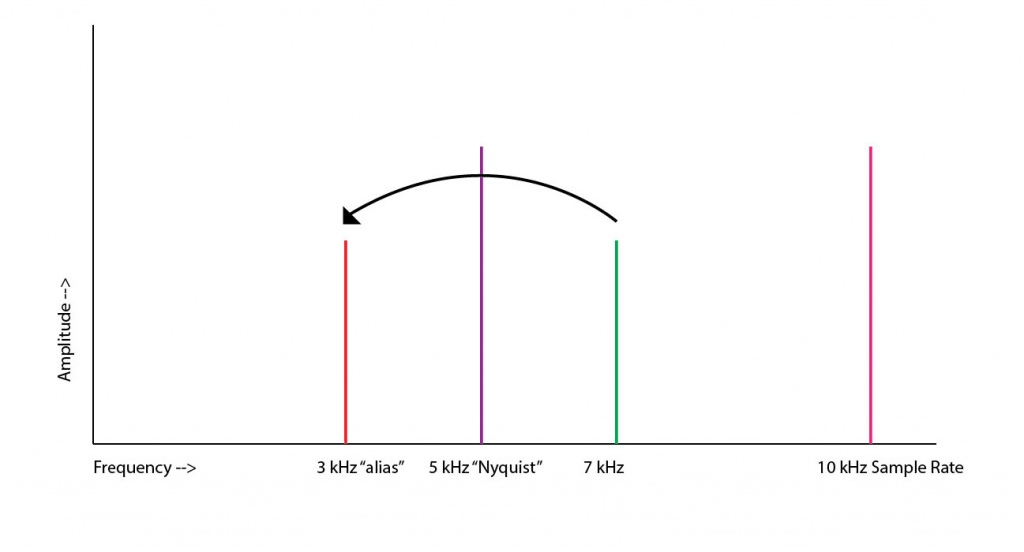
aliasing
-
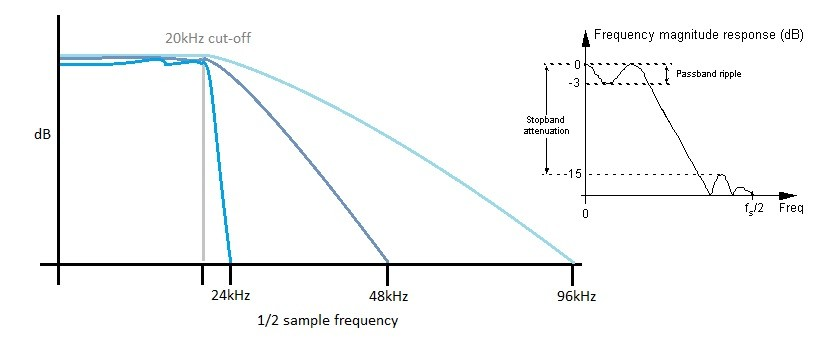
sample rate
-
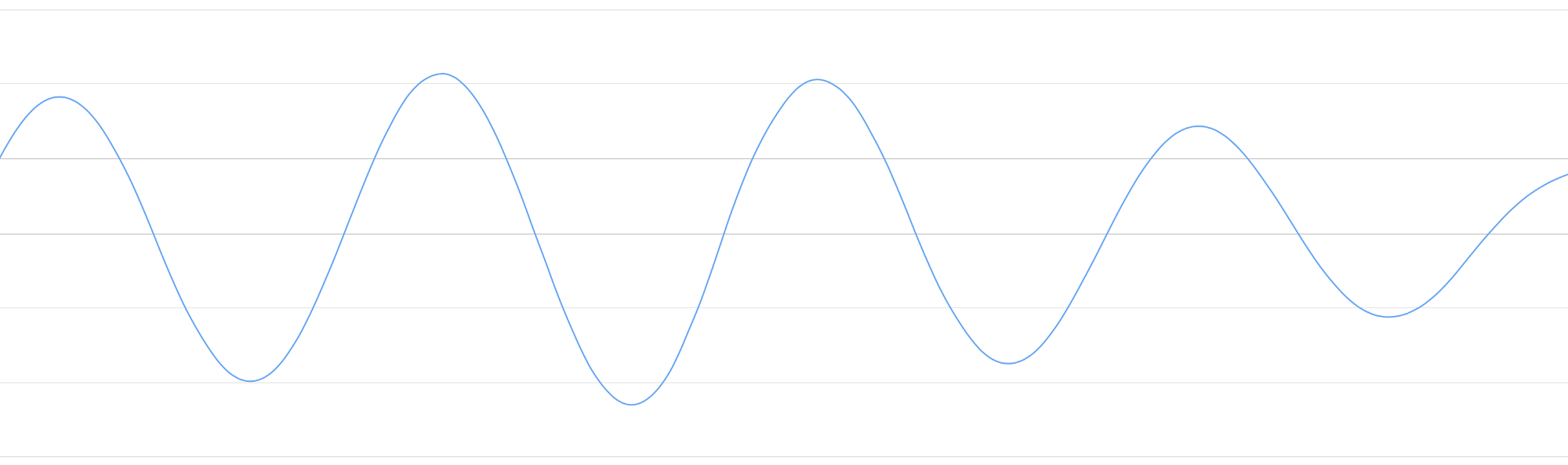
time resolution
-
quantisation
-
dithering
-
encoding
Digital
vs
Analogue
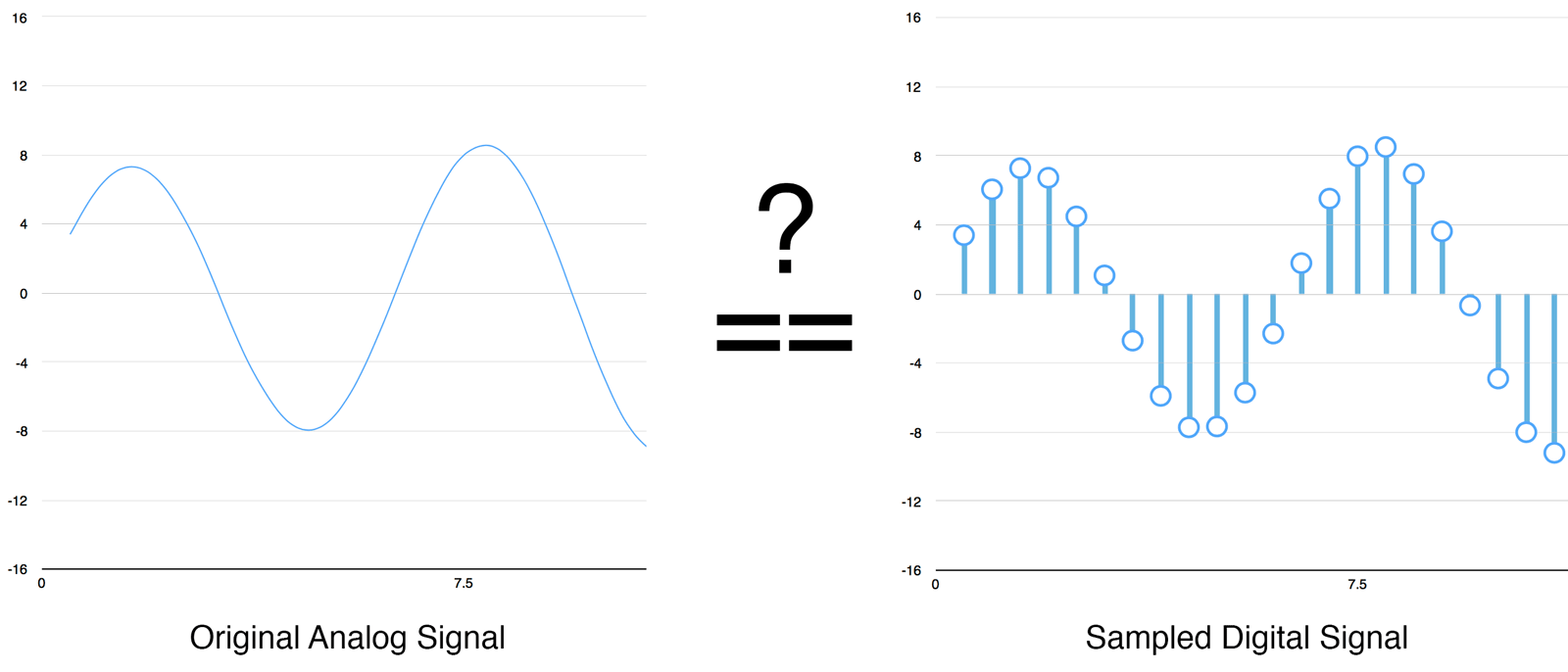
Sampling Theorem
If a function \( x(t) \) contains no frequencies higher than \( \textbf{B} \) hertz, it is completely determined by giving its ordinates at a series of points spaced \( \frac{1}{2\textbf{B}} \) seconds apart.
f_s \geq 2B
Aliasing
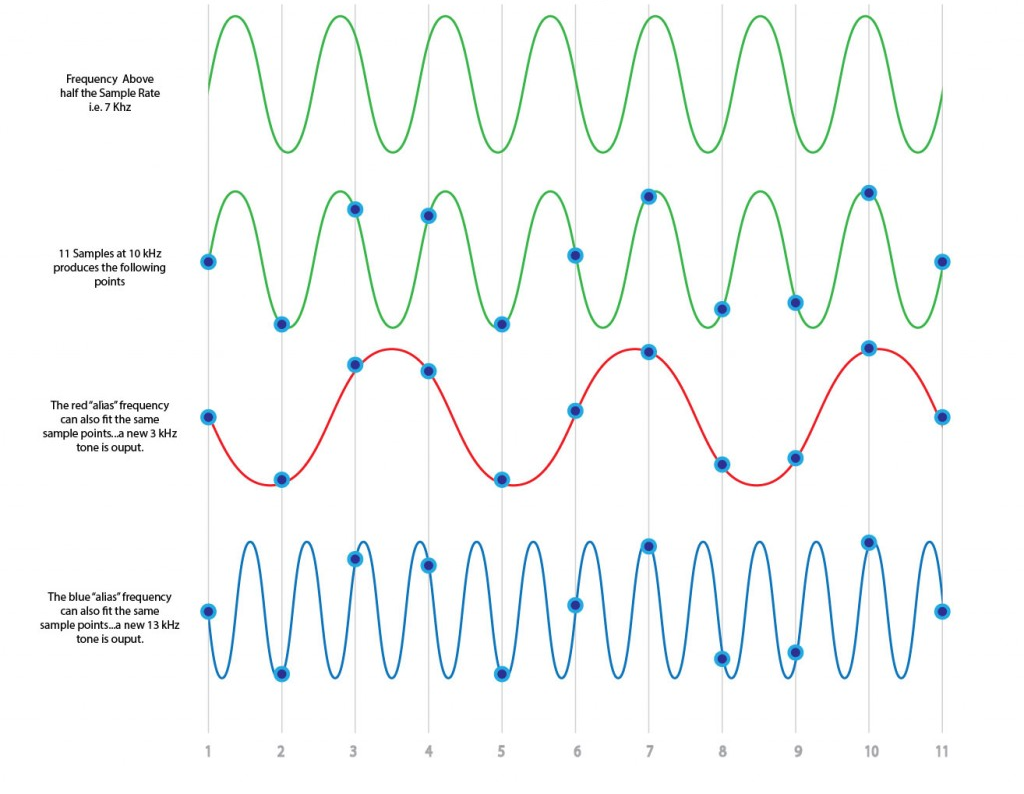
Sample Rate
44,100
Hz
(WTF?)
2^2 \cdot 3^2 \cdot 5^2 \cdot 7^2
...\int e ^xy
NTSC
PAL
245 active lines/field × 60 fields/second × 3 samples/line = 44,100 samples/second
490 active lines per frame, out of 525 lines total
294 active lines/field × 50 fields/second × 3 samples/line = 44,100 samples/second
588 active lines per frame, out of 625 lines total
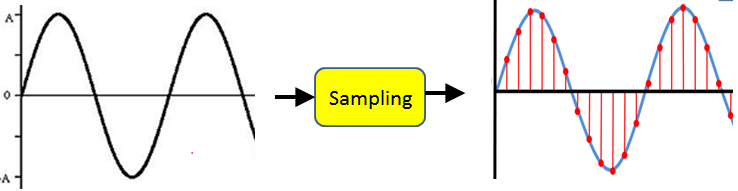
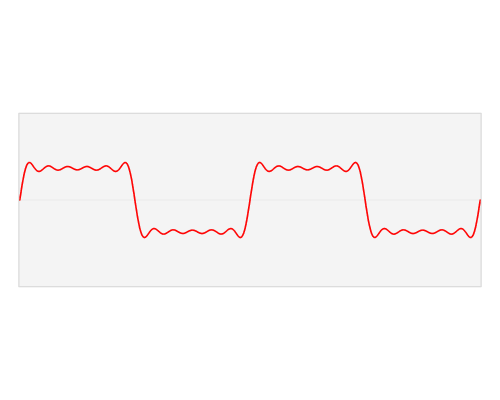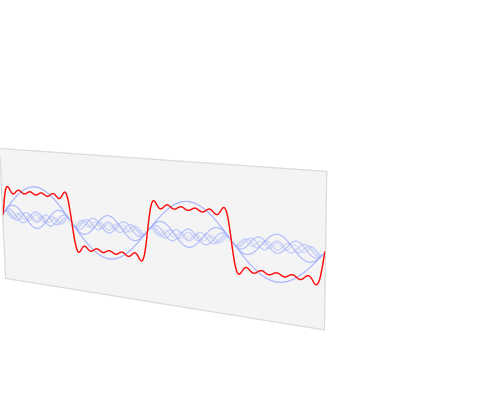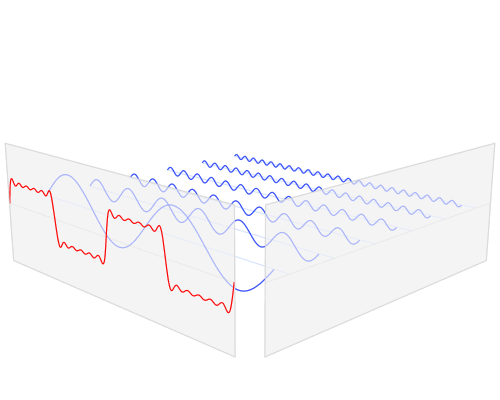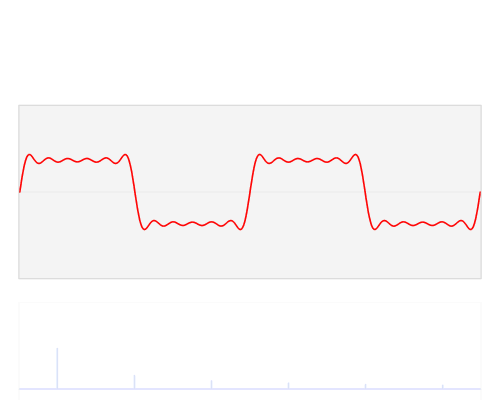
Time Resolution
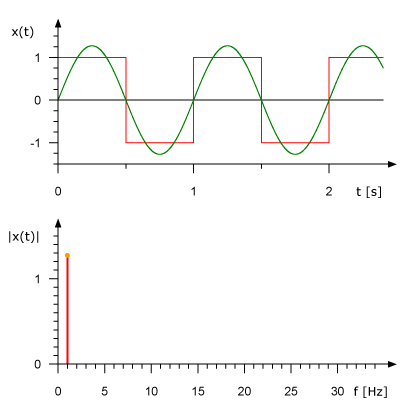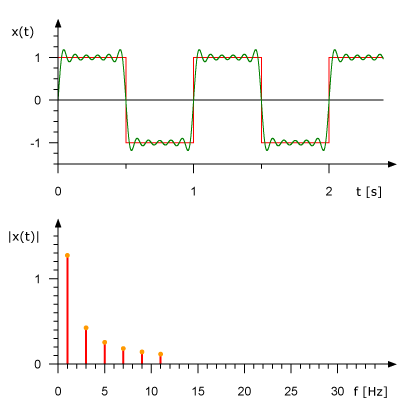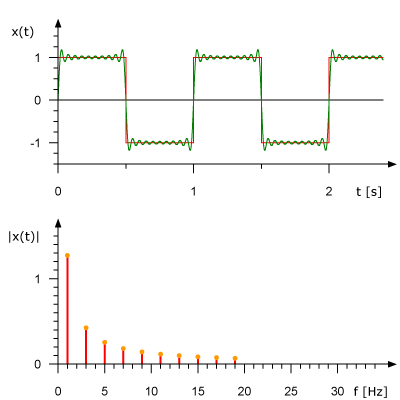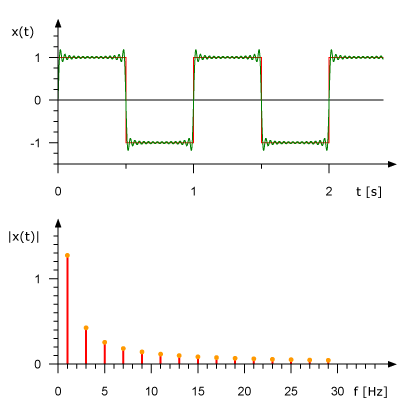
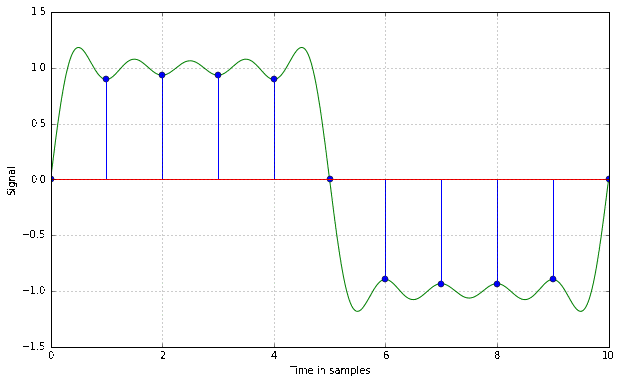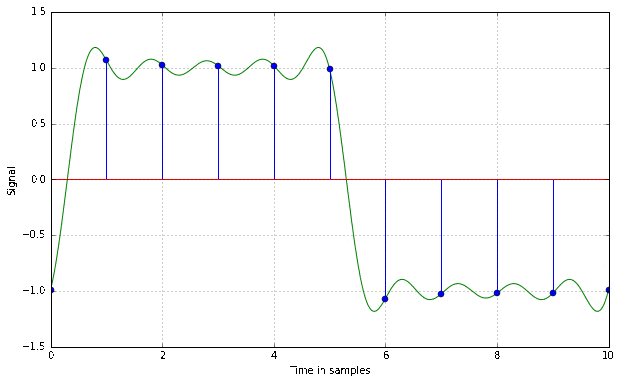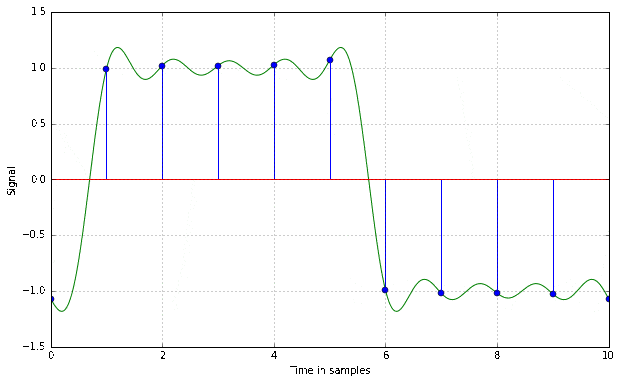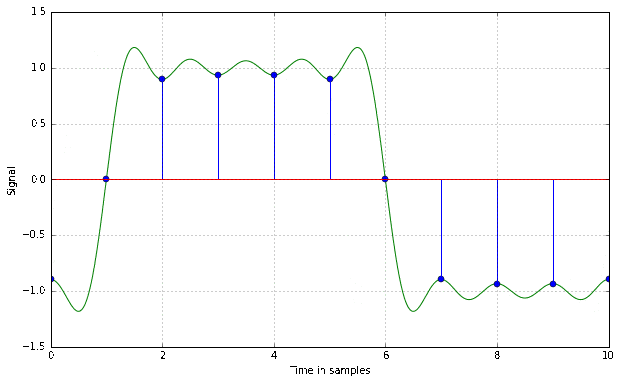
Quantisation
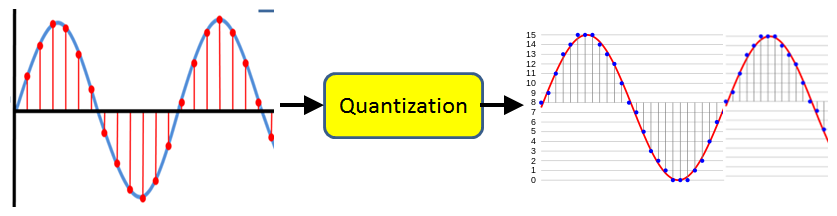
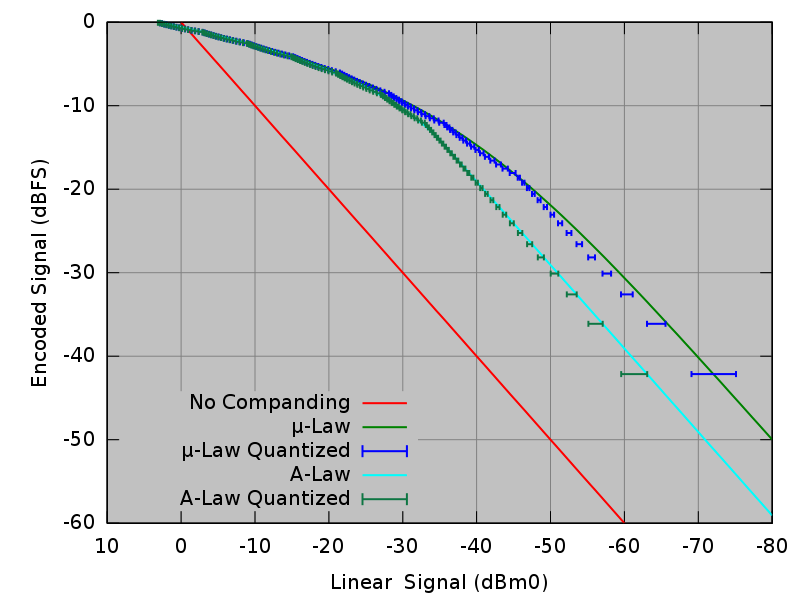
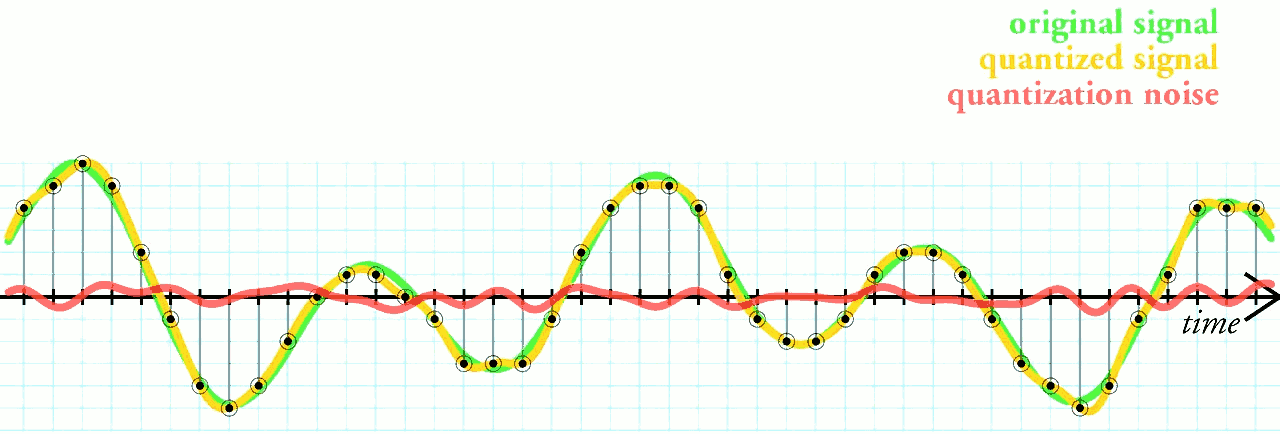
SQNR = 1.76+20\log_{10}(2^N)
SQNR\approx 1.76 + 6.02 \cdot N \text{ dB}
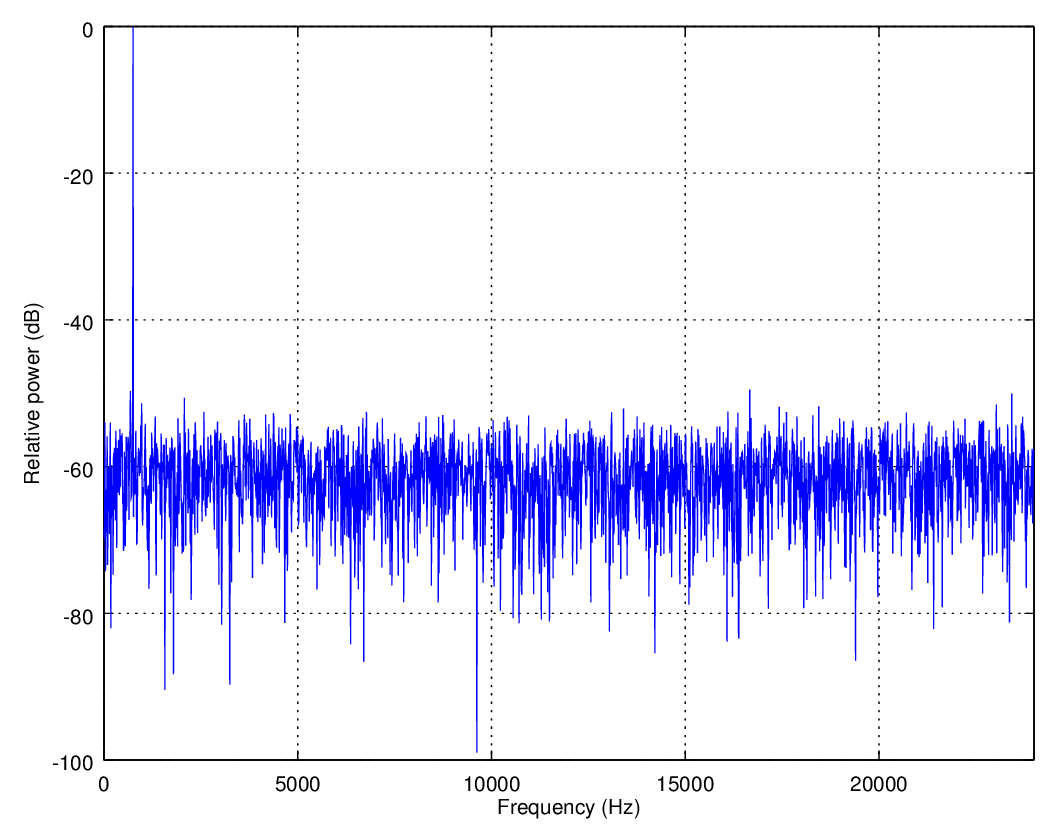
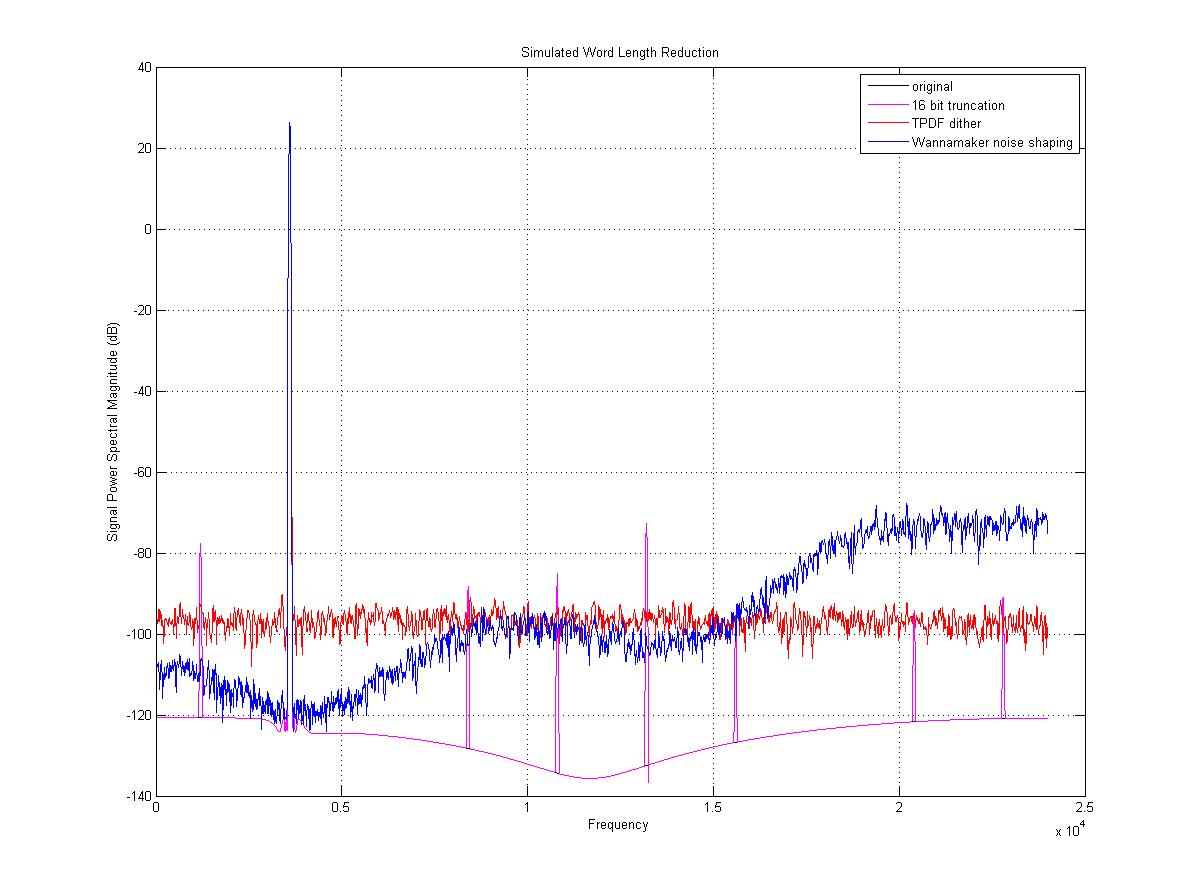
Dithering
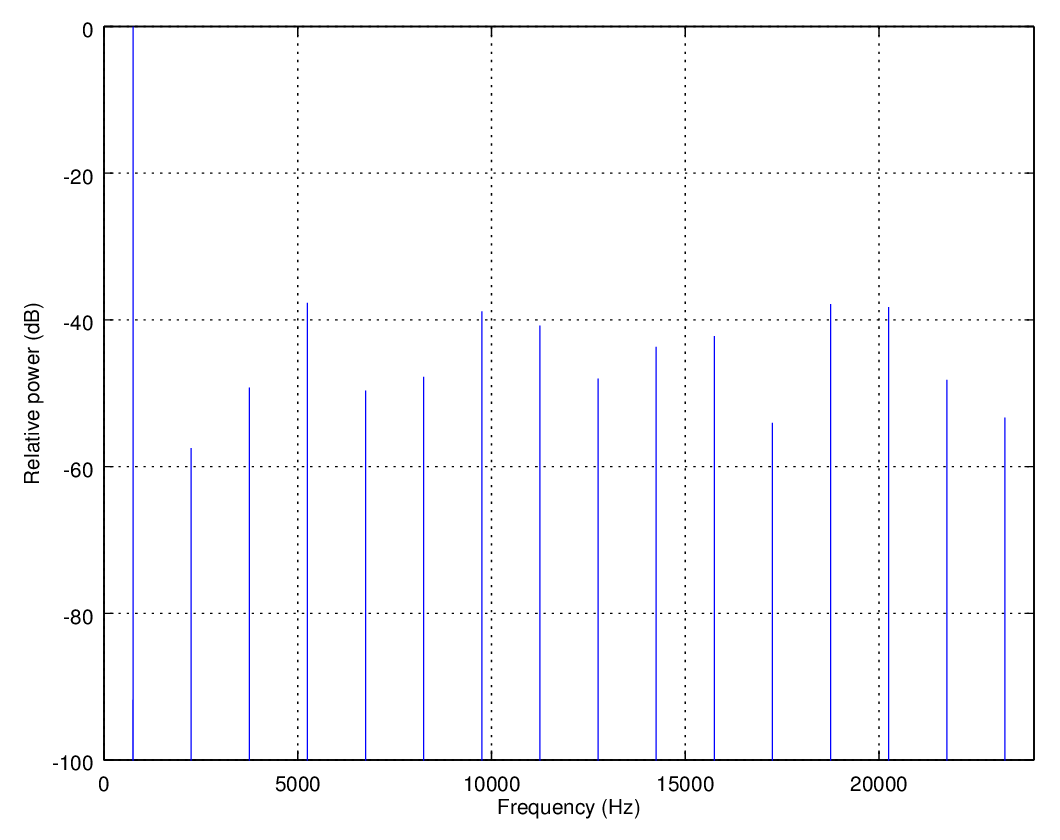
Encoding
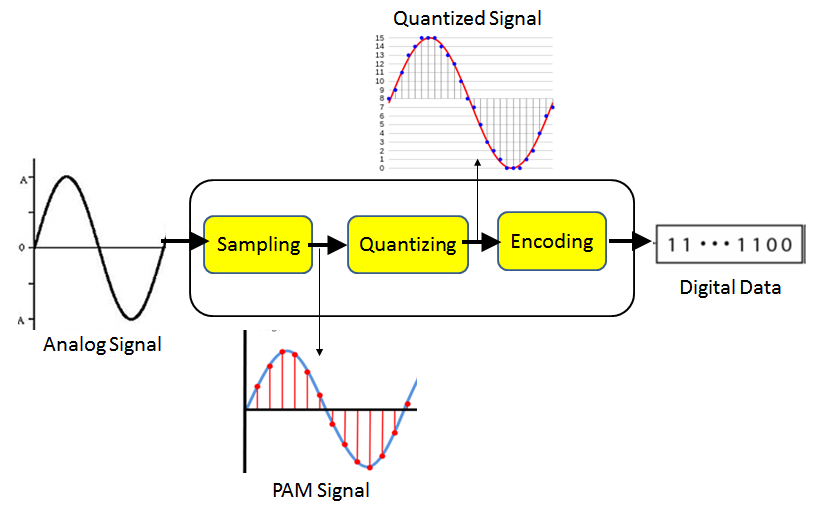
8 bit = \( 2 ^ 8 \) = 256 possible values
16 bit = \(2^{16}\) = 65,536 possible values
24 bit = \( 2 ^ {24} \) = 16,777,216 possible values
32 bit floating point
frequency content \(\propto\) sample rate
dynamic range \(\propto\) bit depth