From random forests to regulatory rules: interpreting supervised learners to guide biological discovery

Karl Kumbier

UC Berkeley Statistics

Advisor: Prof. Bin Yu

 

Generating insights in biology through domain-inspired statistical machine learning

Domain knowledge

Modeling/

analysis

Experimental design/data collection

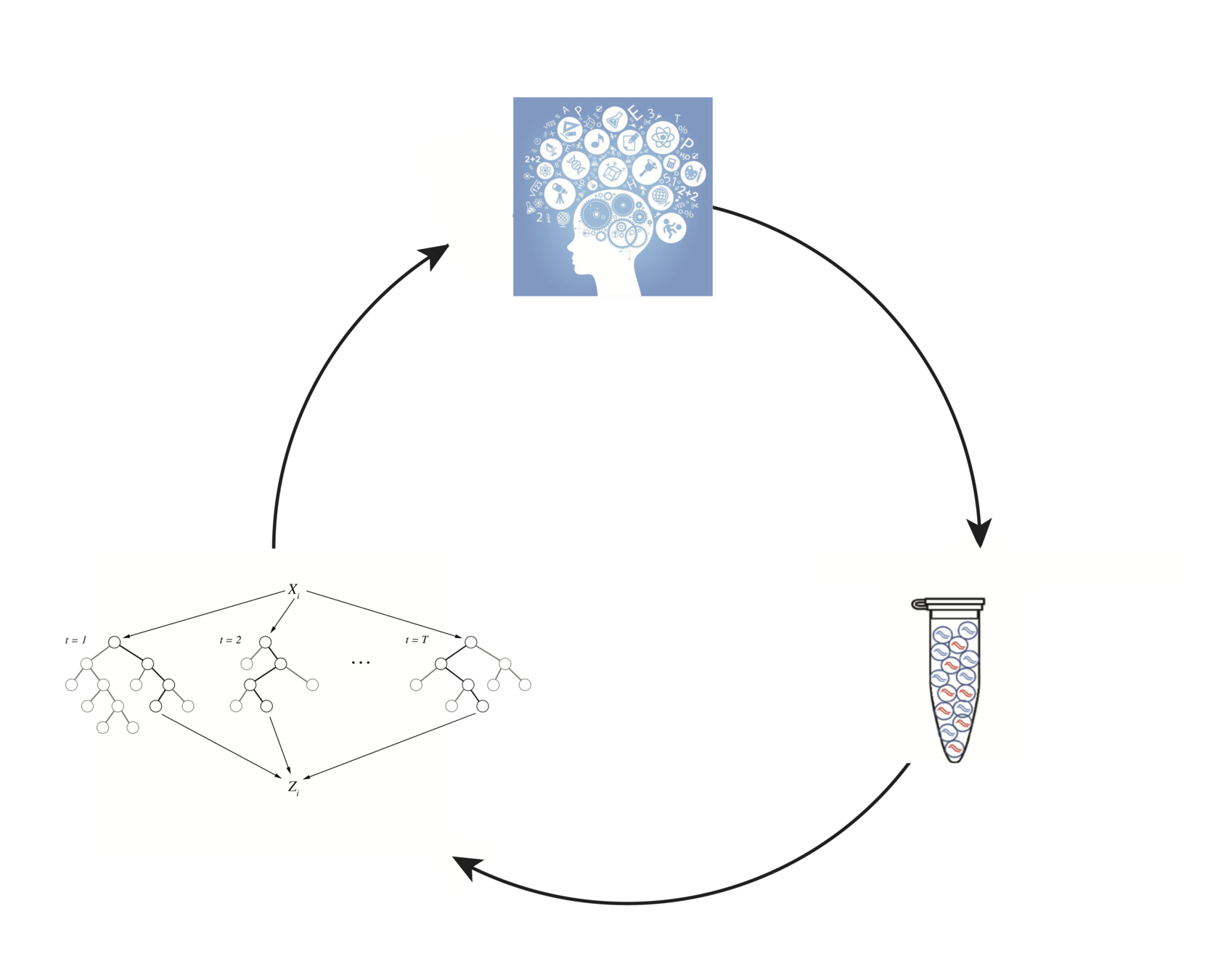
In collaboration with: Susan Celniker (LBNL), James B. Brown (LBNL)

The PCS framework: evaluating human judgement calls in data science

  • Predictability: Does my model reflect external reality?     ​
  • Computability: Can I tractably build/train my model?           
  • Stability: Are my results consistent with respect to "reasonable" perturbations of the data/model?                         

Outline

  • From genomic to statistical interactions

  • Market baskets and genomics

  • Iterative Random Forests

  • Case studies in Drosophila development

From genomic to statistical interactions

Embryonic development in Drosophila

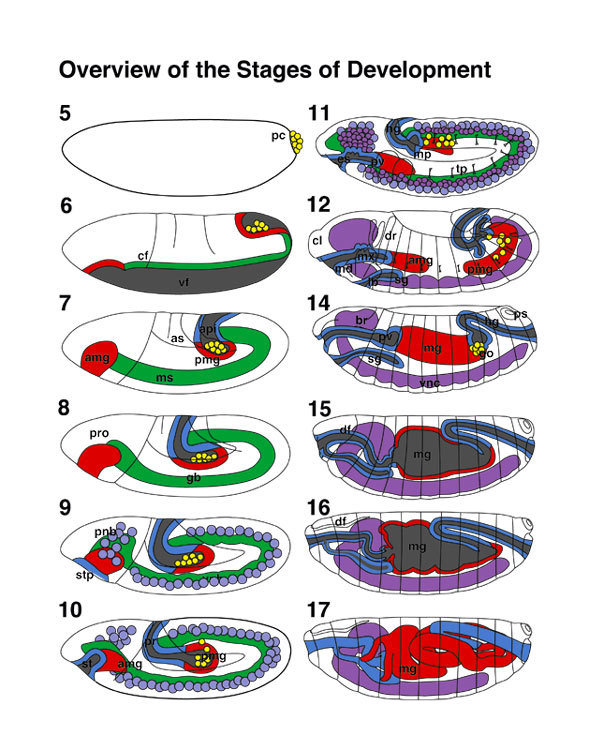
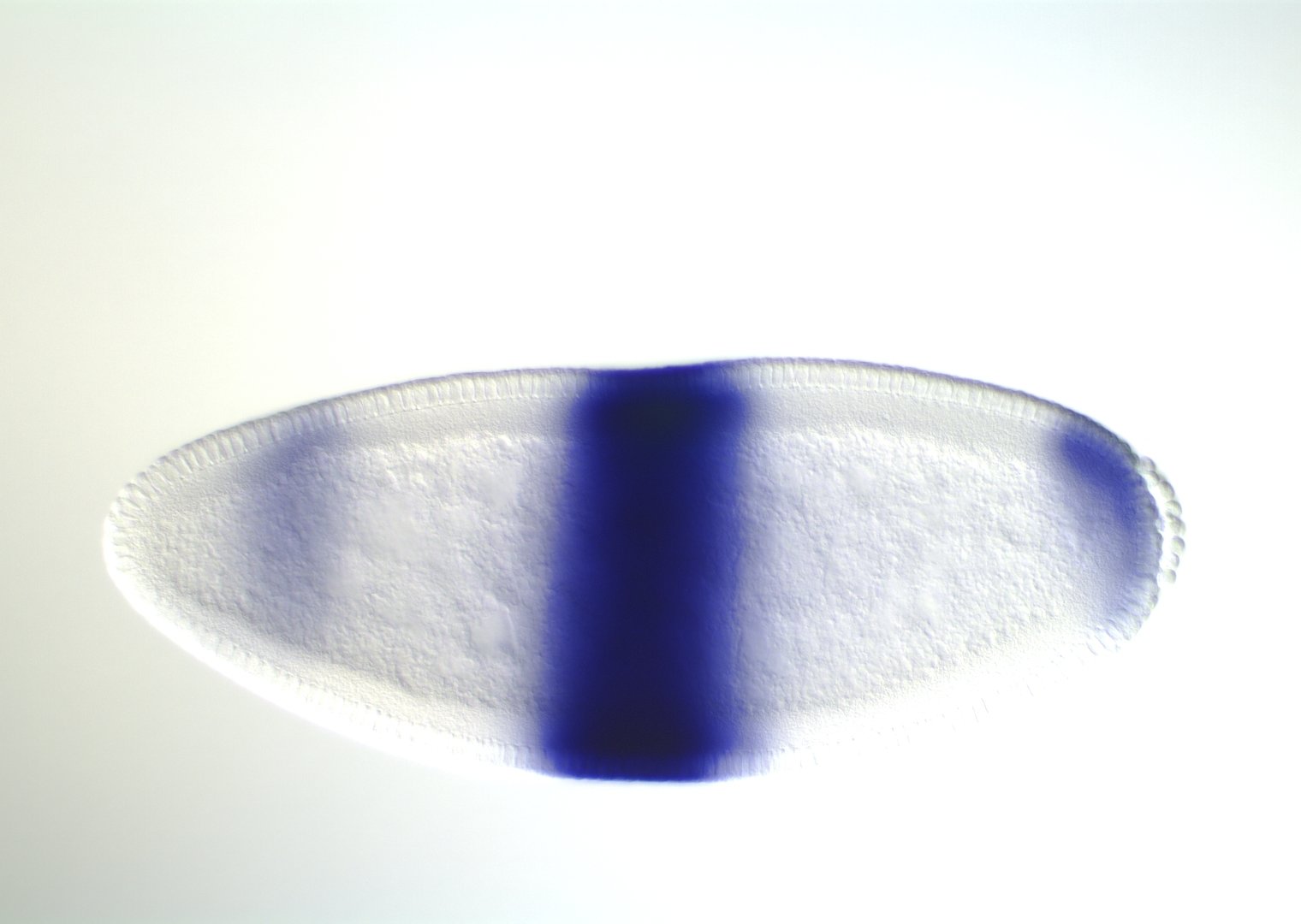
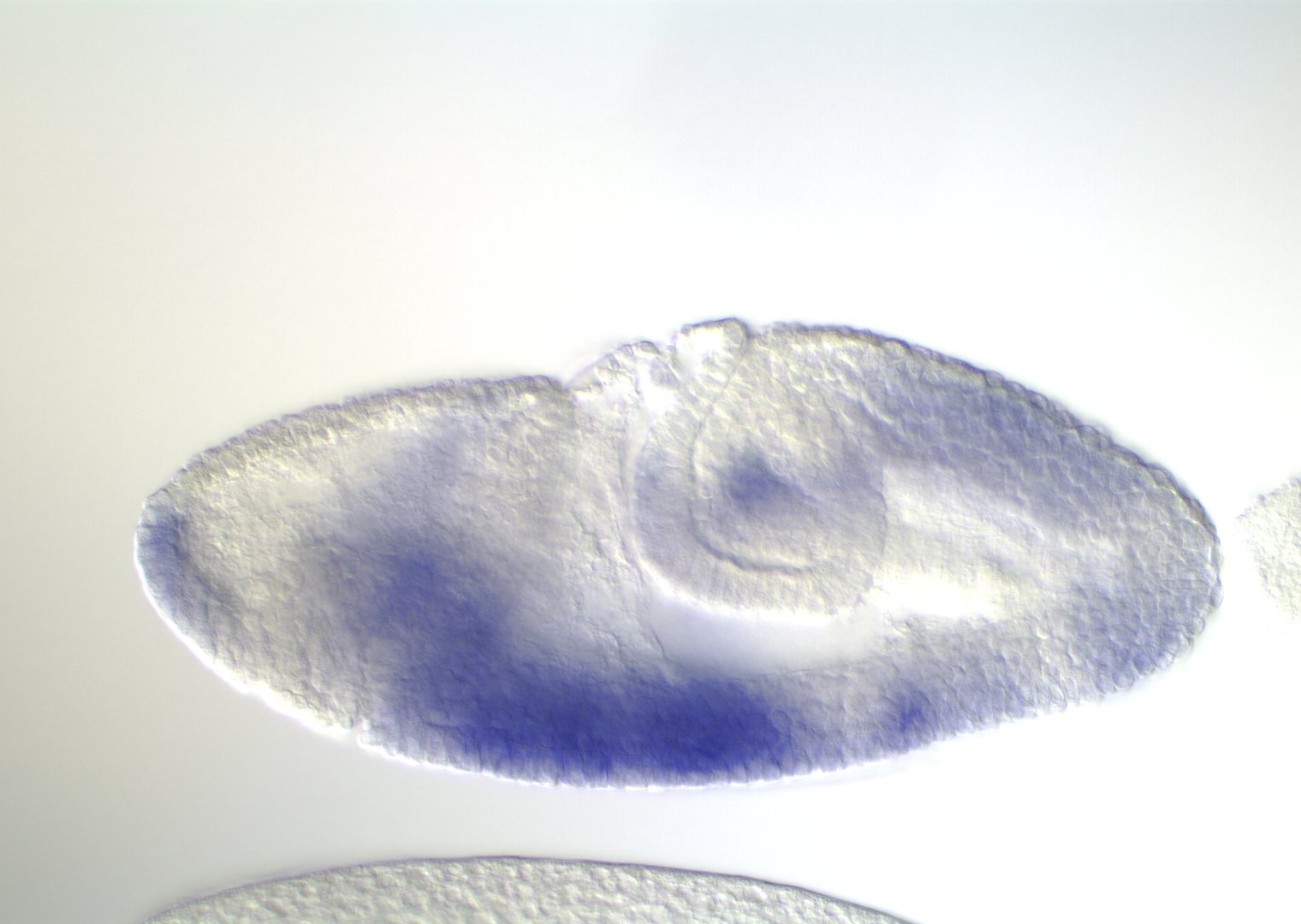
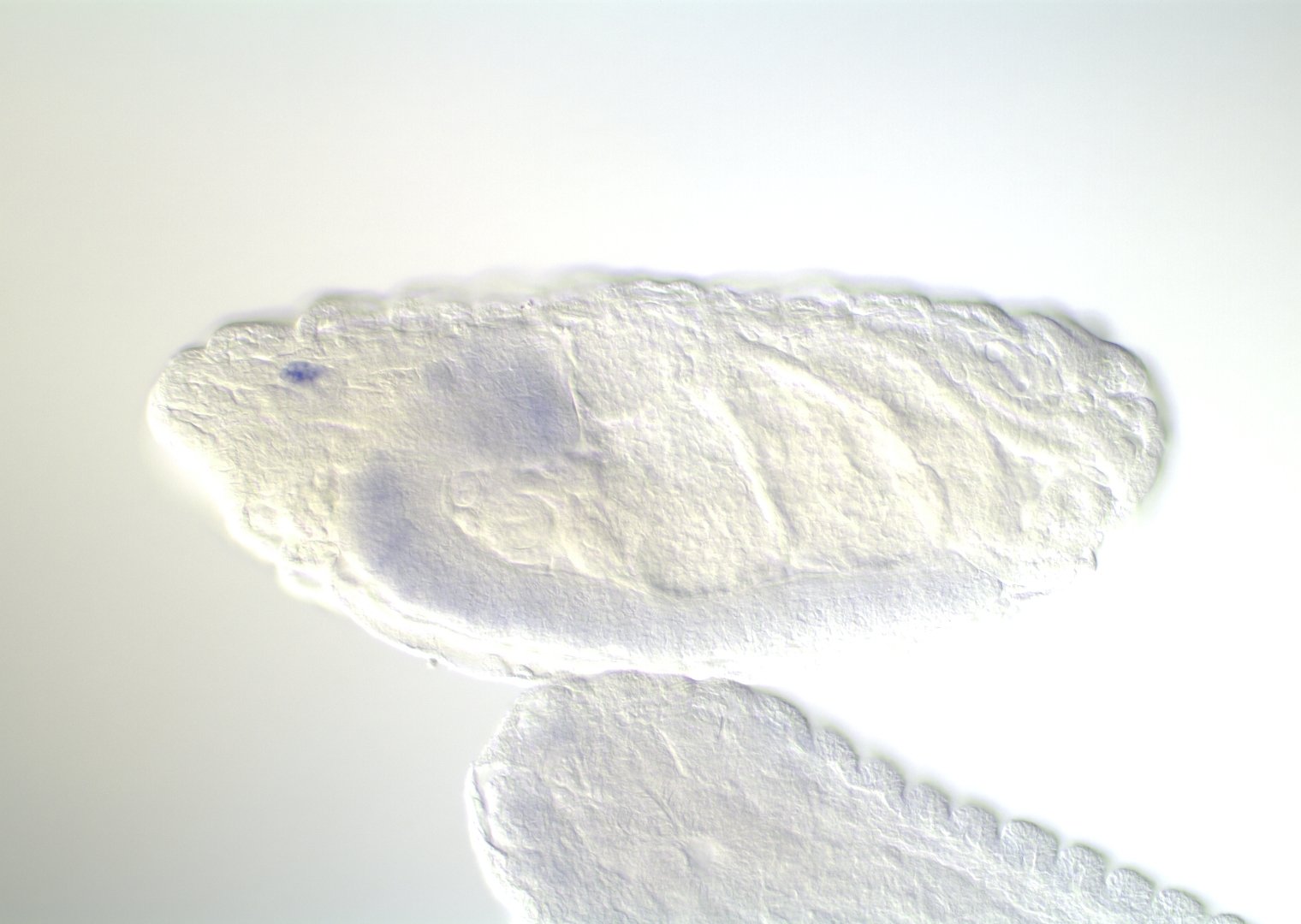
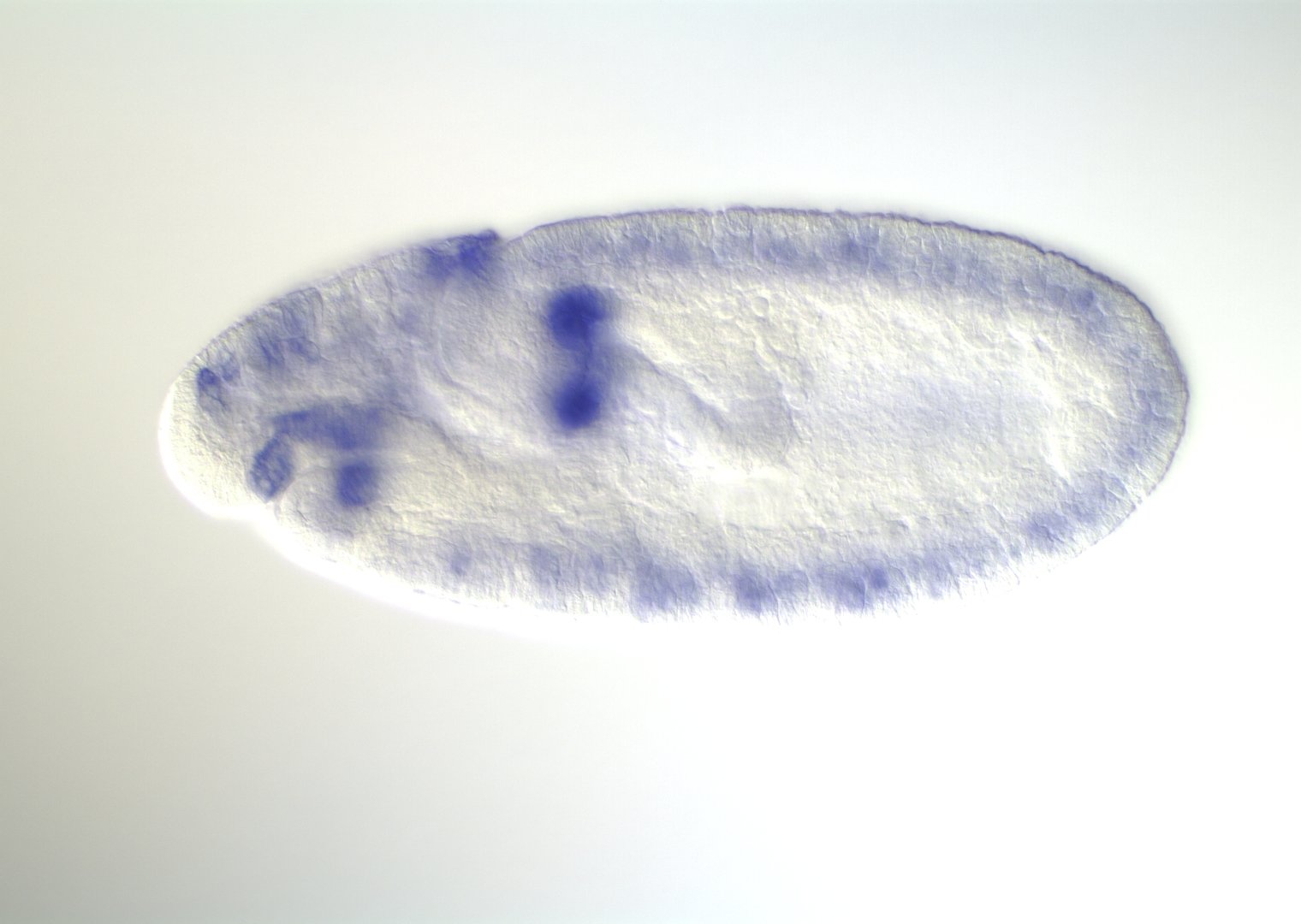
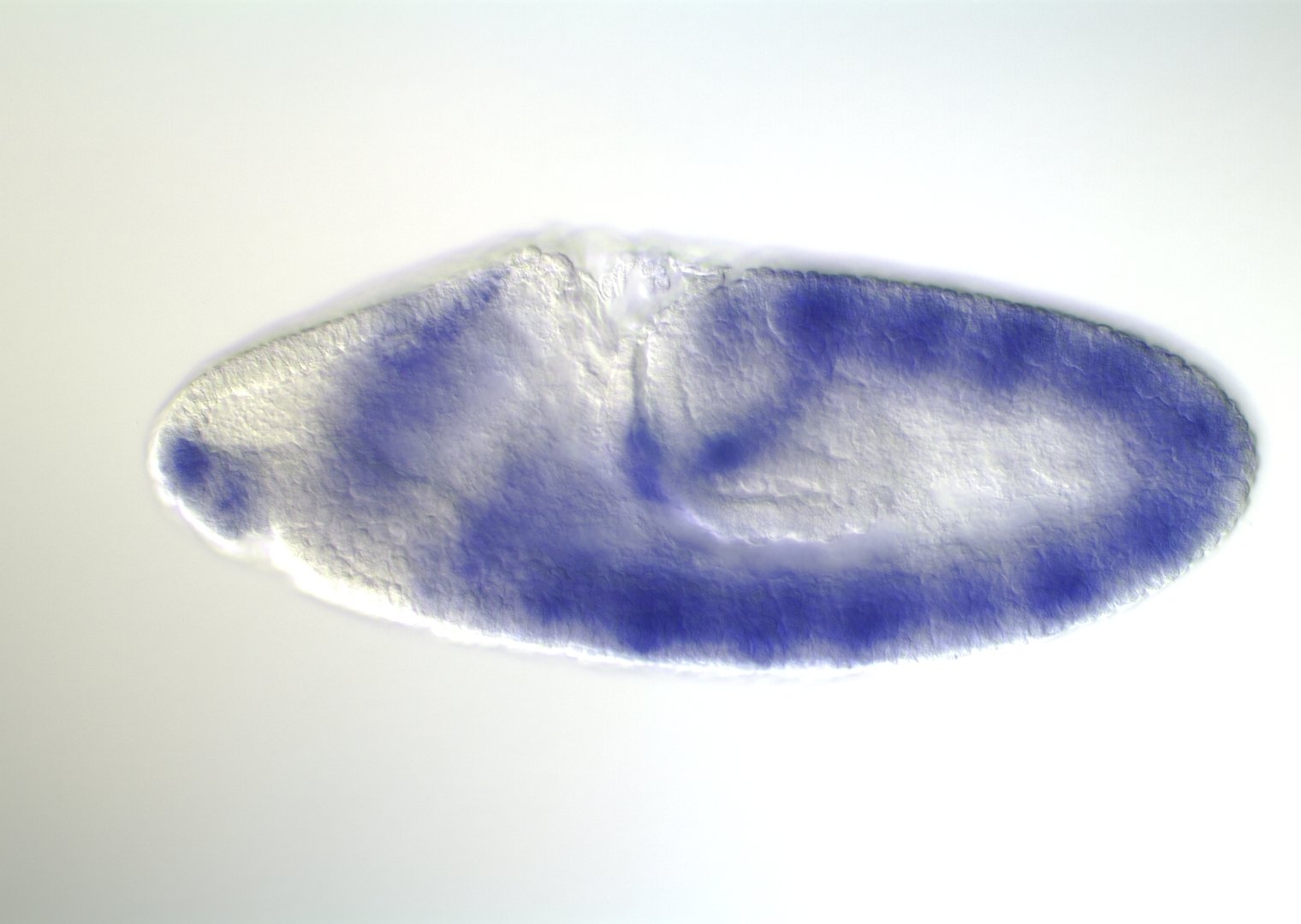
0-1:20 hours

1:20-3:00 hours

3:00-3:40 hours

3:40-5:20 hours

5:20-9:00 hours

9:20-16:00 hours

image: Volker Hartenstein

images: BDGP

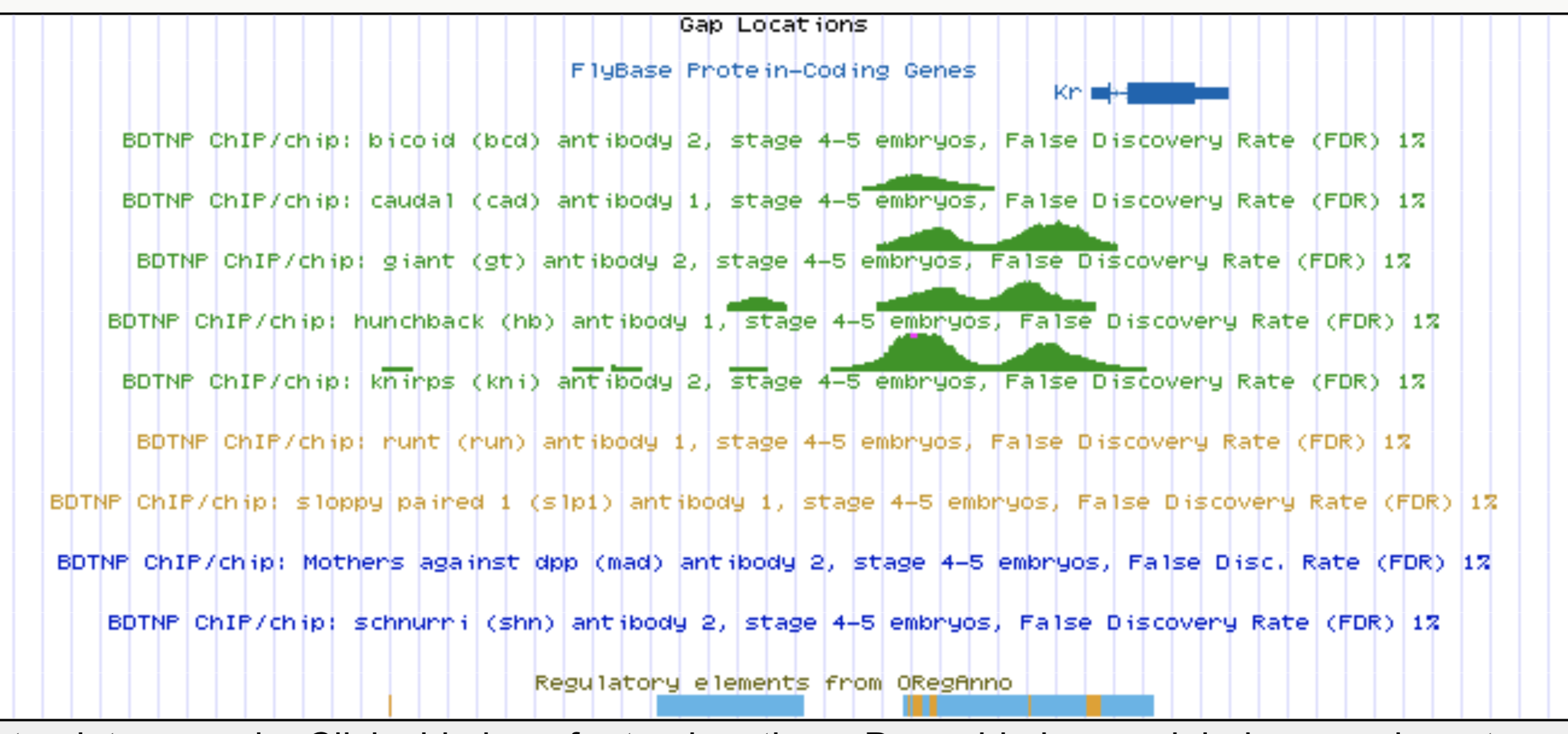
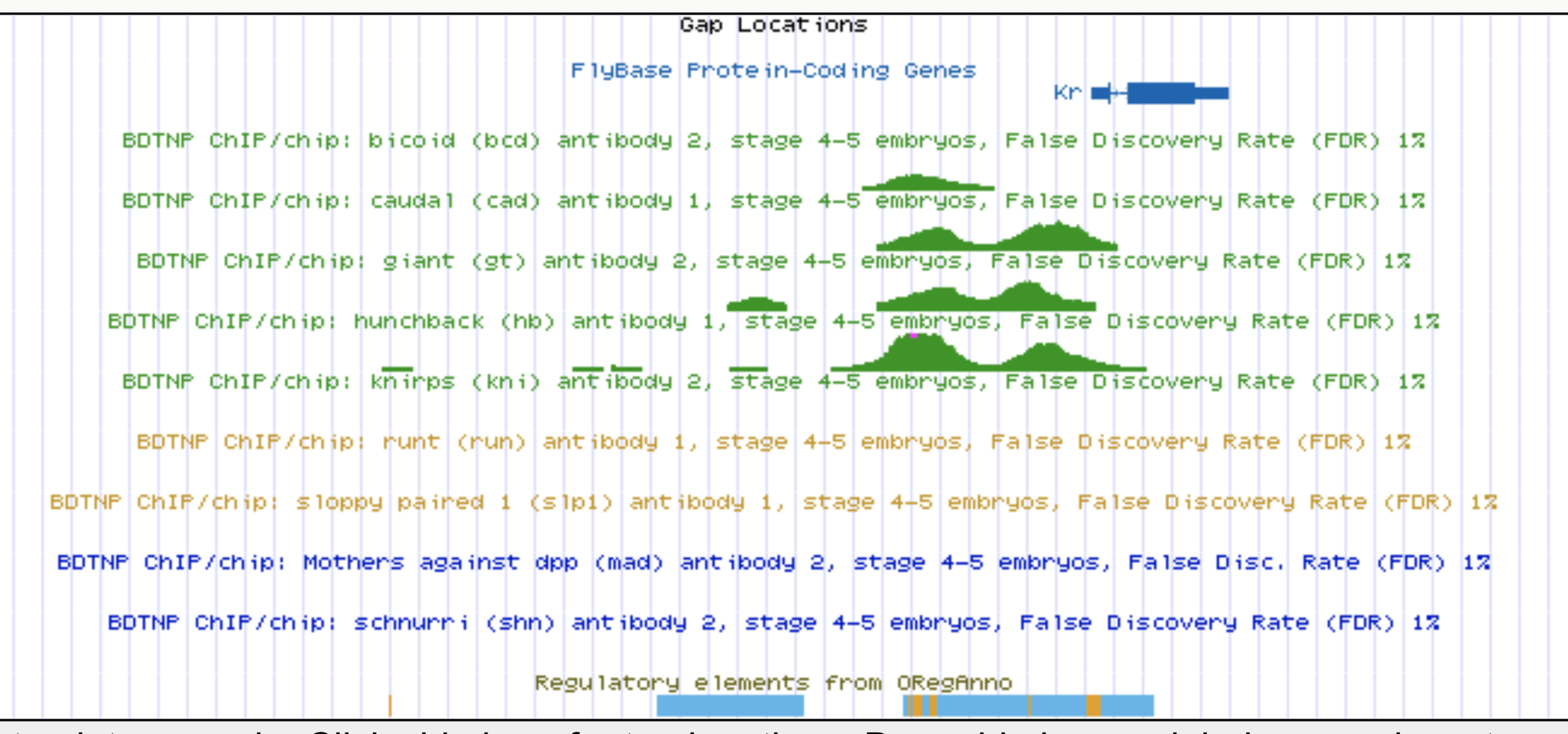
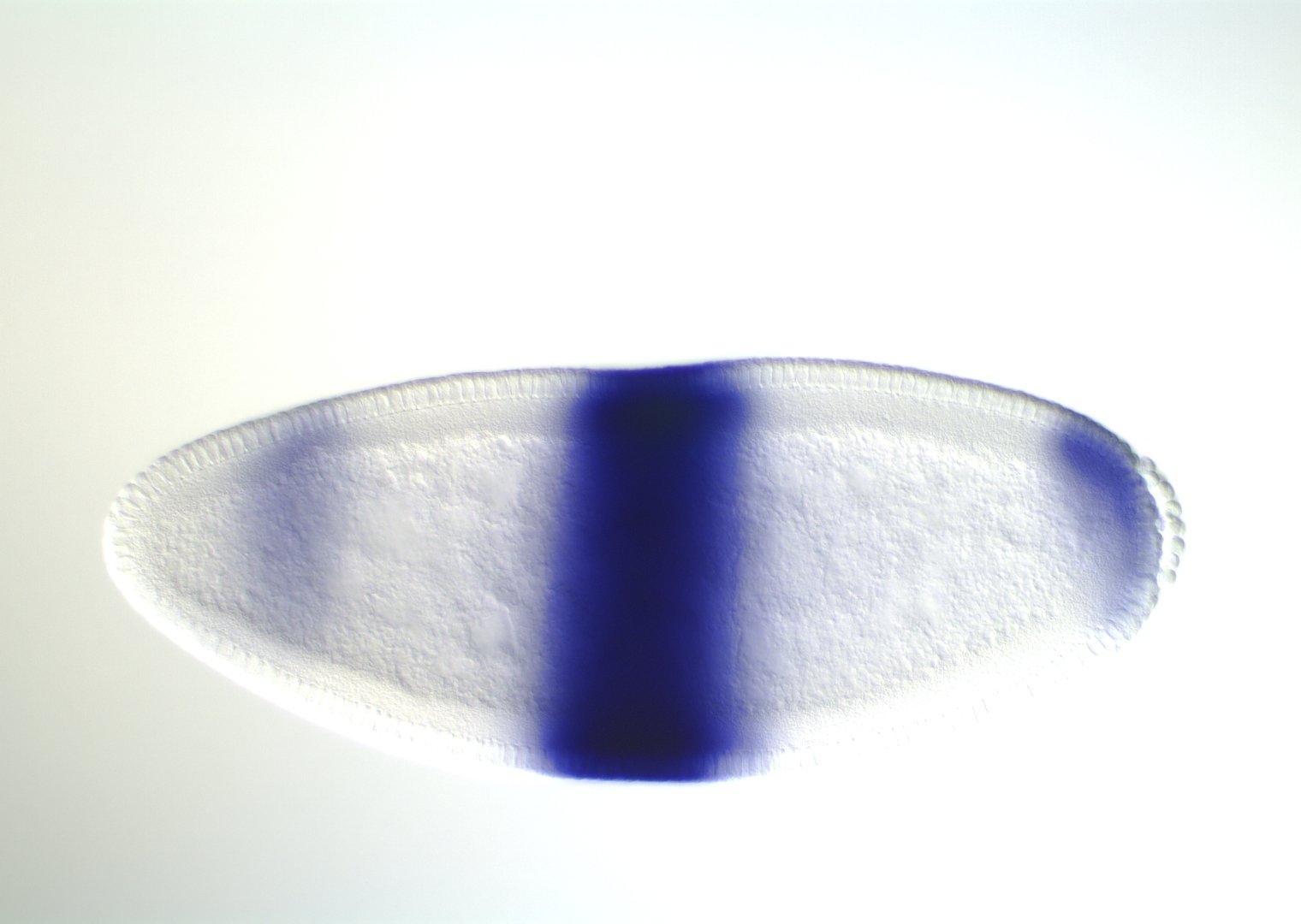
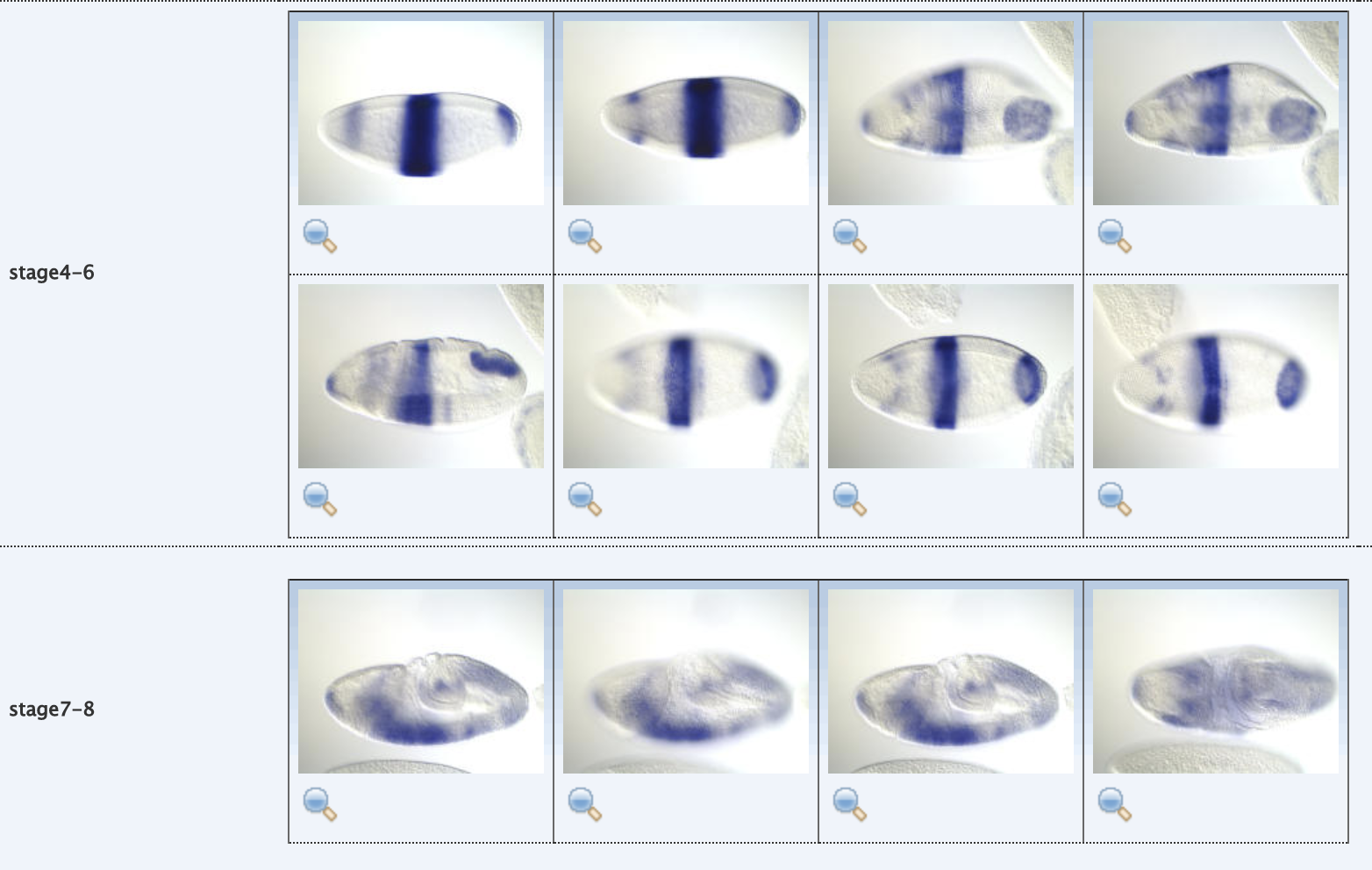
 Kr expression

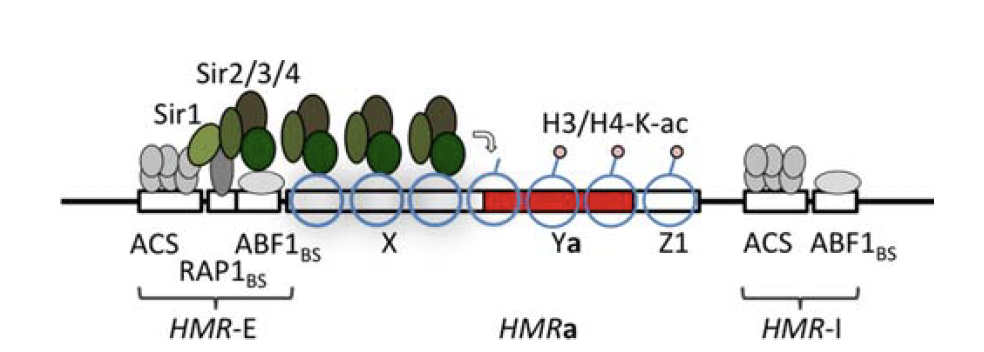
Enhancers regulate spatio-temporal programs of gene expression

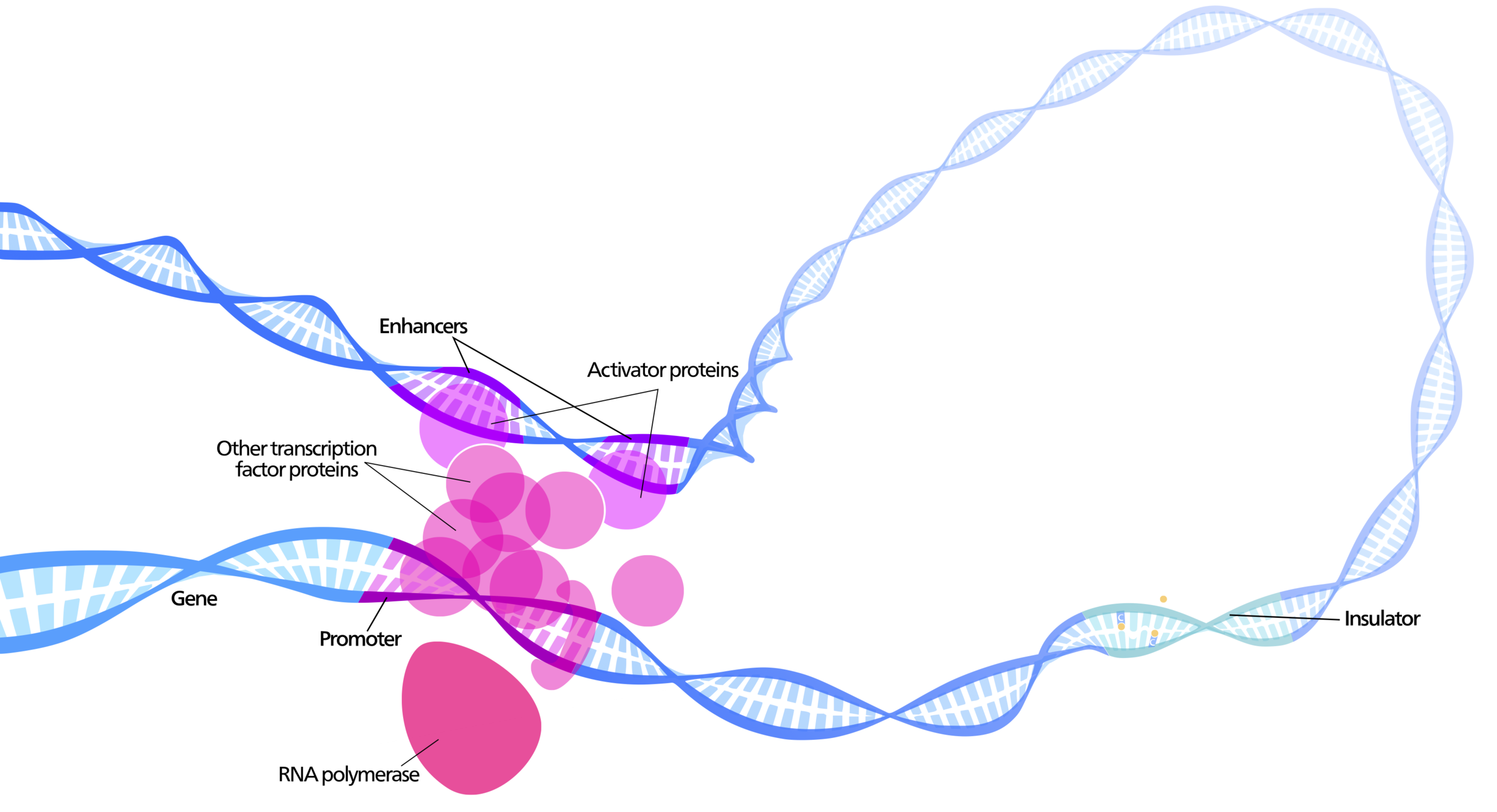
Enhancers: segments of the genome that coordinate transcription factor (TF) activity to regulate gene expression.

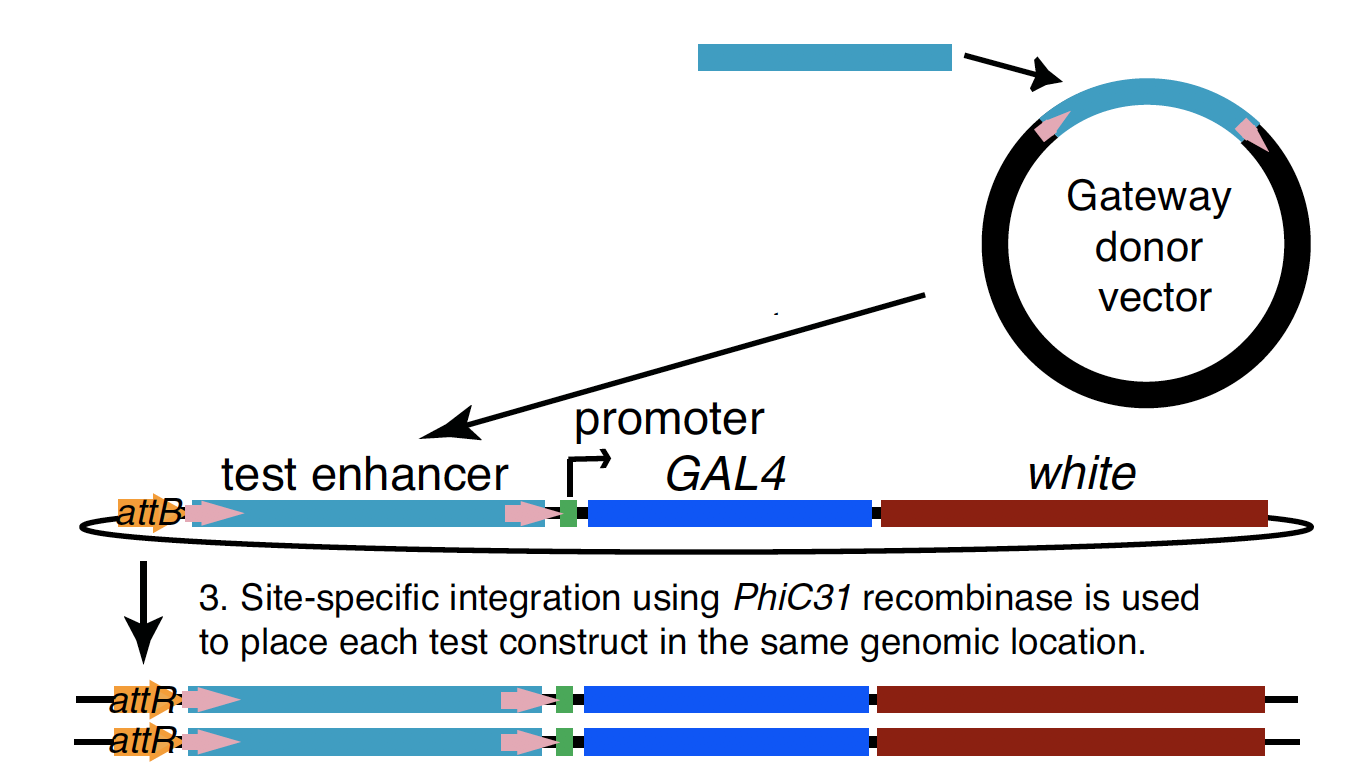
Experimental evaluation of enhancer elements in Drosophila

Pfeiffer et al. (2008)

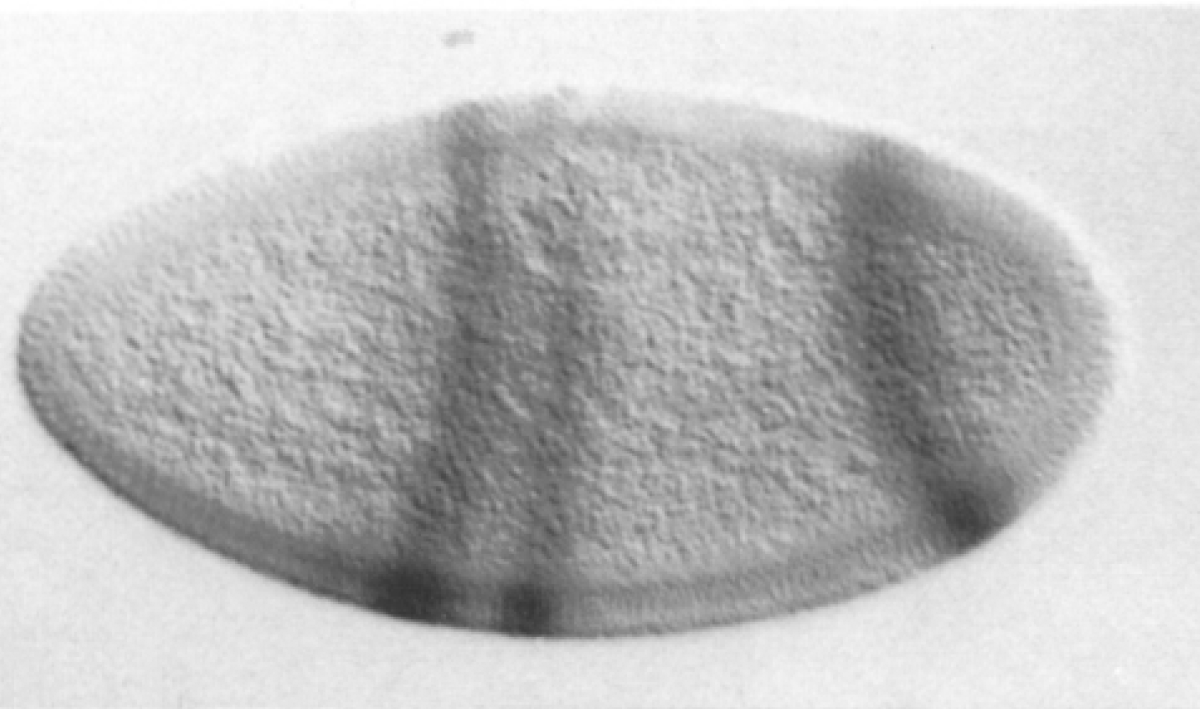
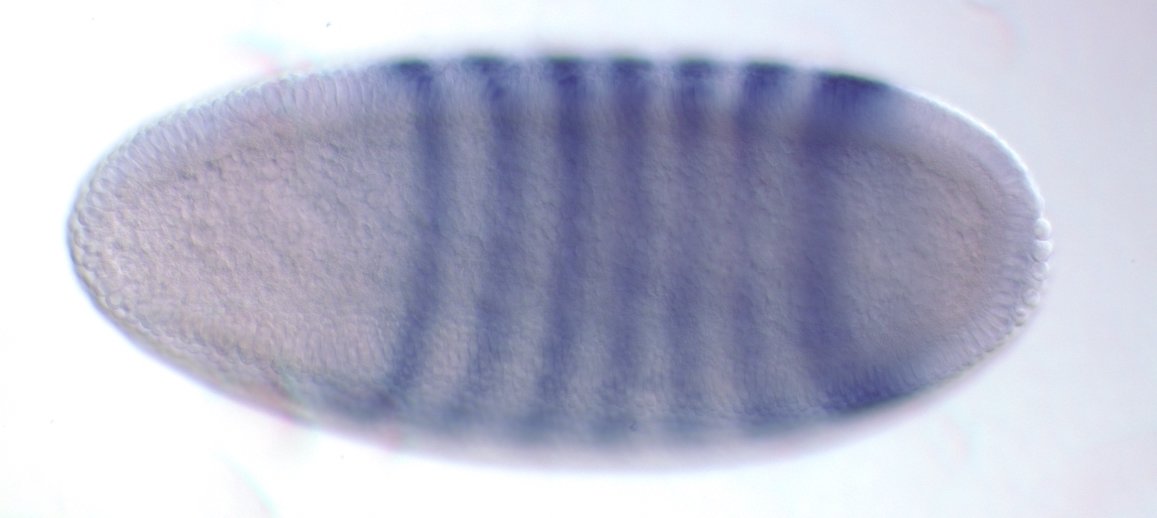
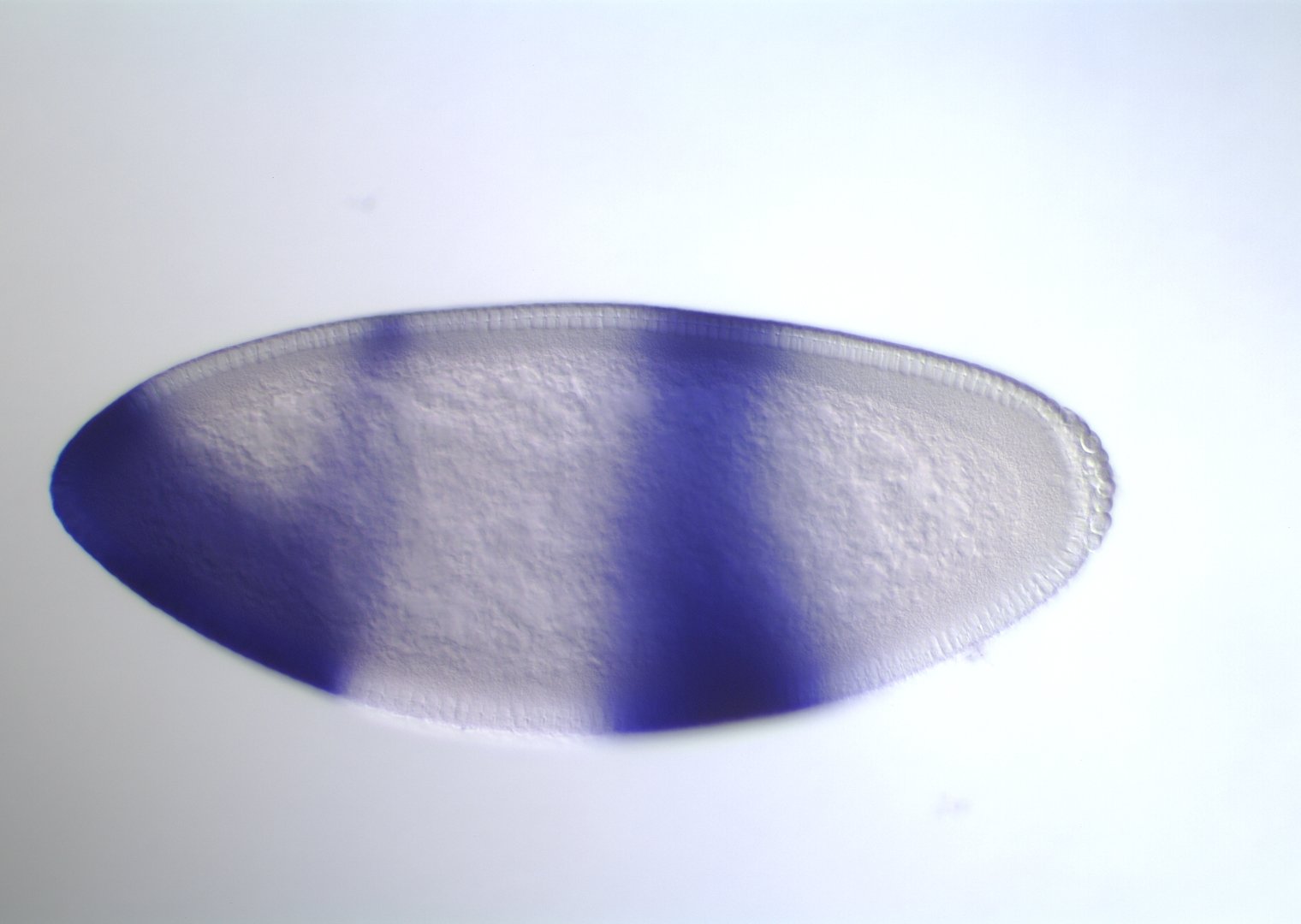
even-skipped

expression

wt

transgenic

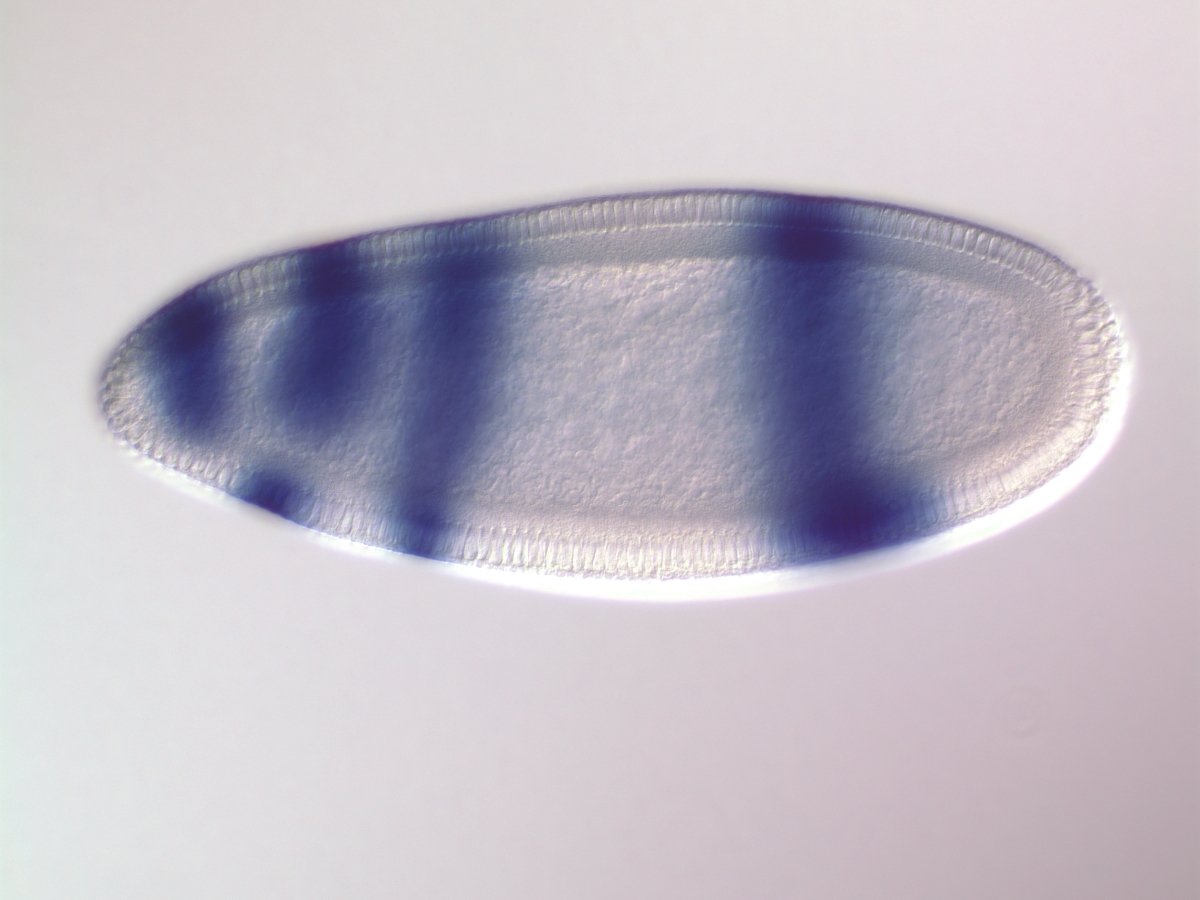
Experimental evaluation of enhancer elements in Drosophila

Hiromi et al. (1985), Harding et al. (1989), Goto et al. (1989), Pfeiffer et al. (2008)

even-skipped expression

wt

transgenic

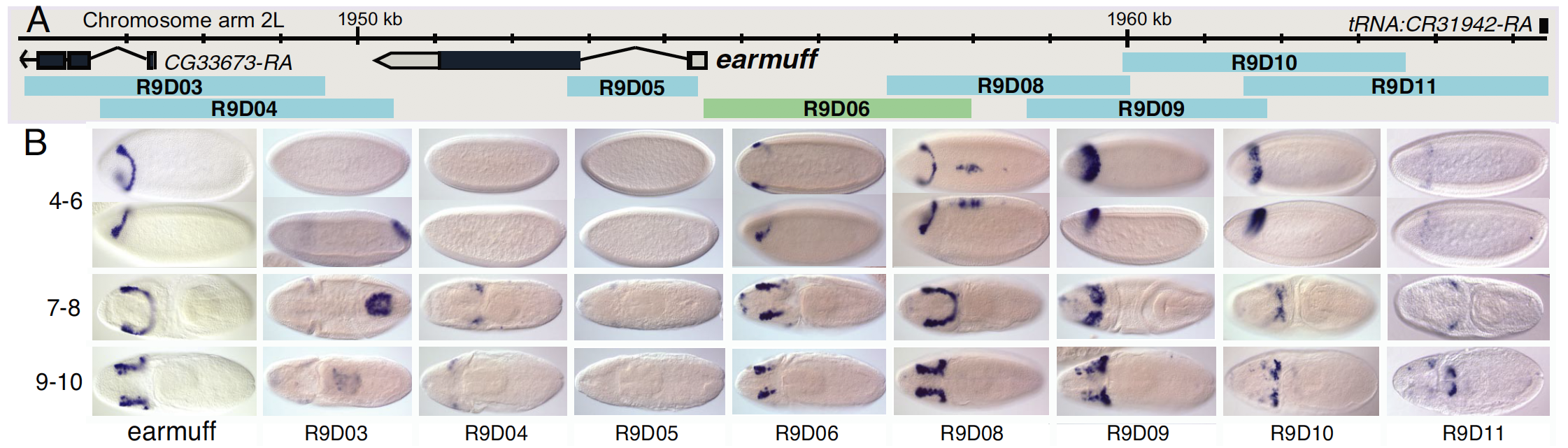
High-order interactions at enhancer elements drive embryonic development

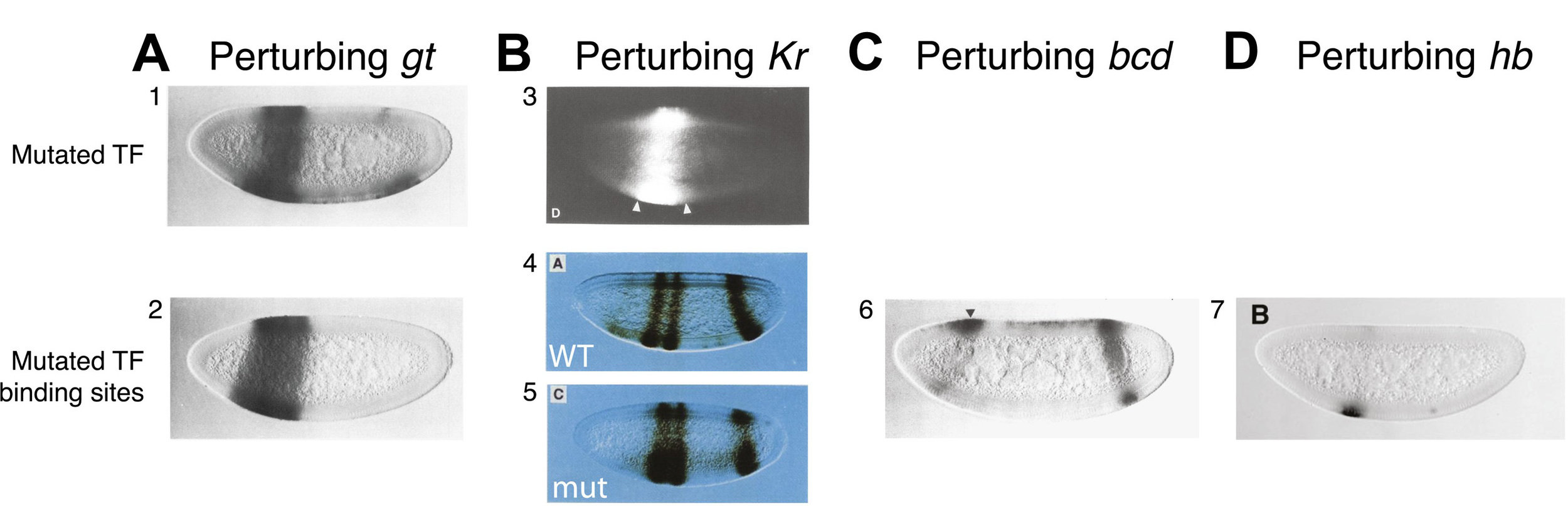
Goto et al. (1989), Harding et al. (1989), Small et al. (1992), Isley et al. (2013), Levine et al. (2013)

Identifying regulatory interactions from high-throughput genomic data

Experimentally validated enhancer elements.

Whole-embryo ChIP-chip/ChIP-seq measurements of transcription factor (TF) DNA binding

From genomic to statistical interactions

r(\mathbf{x})=
r(x)=r(\mathbf{x})=
\prod_{j\in\text{A}} 1(x_j > t_j)
∏j∈A1(xj>tj)\prod_{j\in\text{A}} 1(x_j > t_j)
\cdot
⋅\cdot
\prod_{j\in\text{R}} 1(x_j \le t_j)
∏j∈R1(xj≤tj)\prod_{j\in\text{R}} 1(x_j \le t_j)

activators

repressors

\mathbf{x}=(x_1, \dots, x_p)
x=(x1,…,xp)\mathbf{x}=(x_1, \dots, x_p)

Segment of the genome

DNA binding for p transcription factors (TFs)

Order-s interaction: s = #activators + #repressors

r(\mathbf{x}) = 1
r(x)=1r(\mathbf{x}) = 1
x_{bcd}
xbcdx_{bcd}
x_{cad}
xcadx_{cad}
\dots
…\dots

Thresholding rules define expression domains

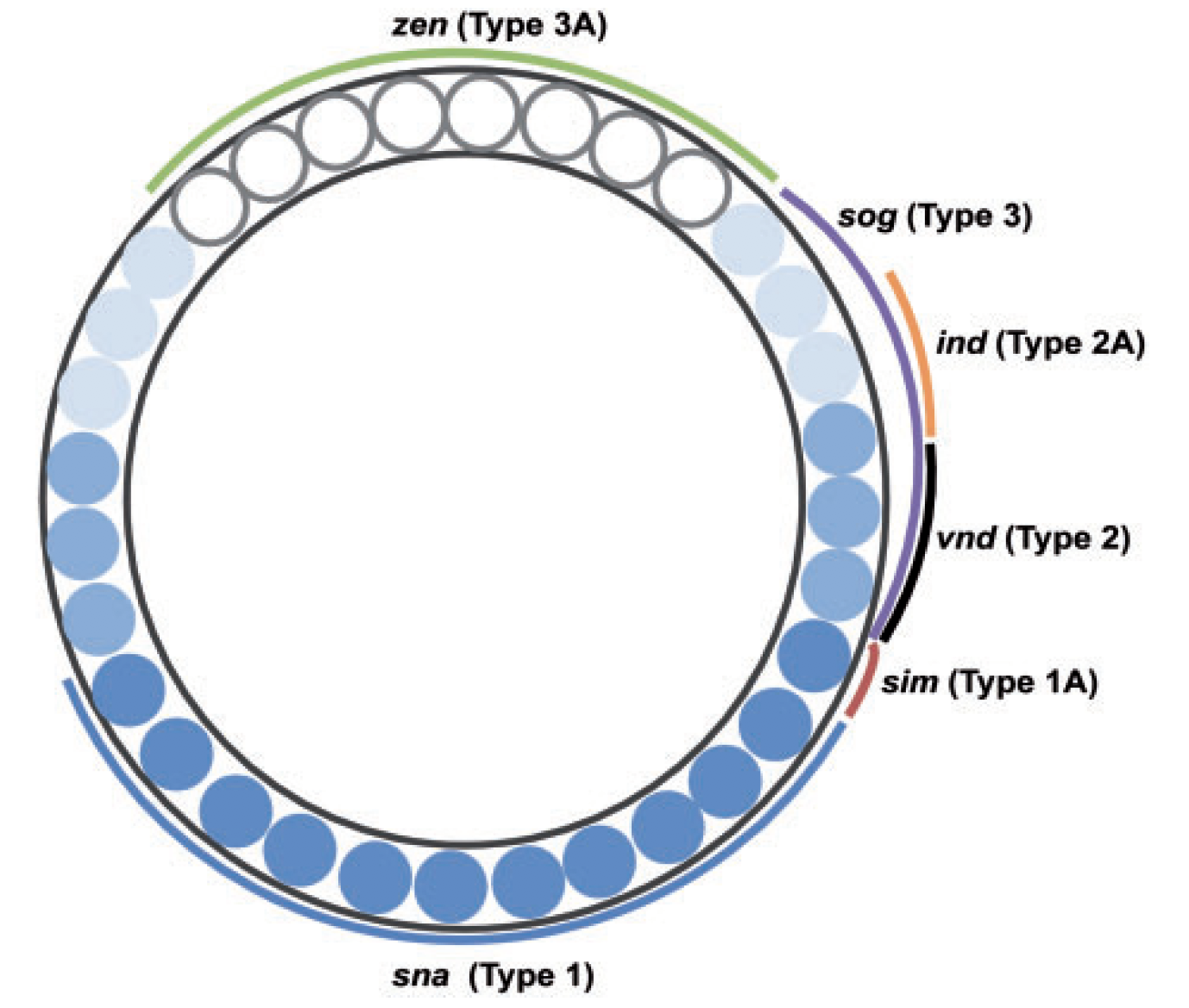
Chopra and Levine (2009)

Dl +

Dl -

Wolpert (1968), Jaeger and Reinitz (2006), Chopra and Levine (2009), Zizen et al. (2009), Knowles and Biggin (2013), Levine (2013), Staller al. (2015), ...

Jaeger and Reinitz (2009)

From genomic to statistical interactions

\mathbb{P}_n(y = 1 | S)
Pn(y=1∣S)\mathbb{P}_n(y = 1 | S)
\mathbb{P}_n(S|y = 1)
Pn(S∣y=1)\mathbb{P}_n(S|y = 1)

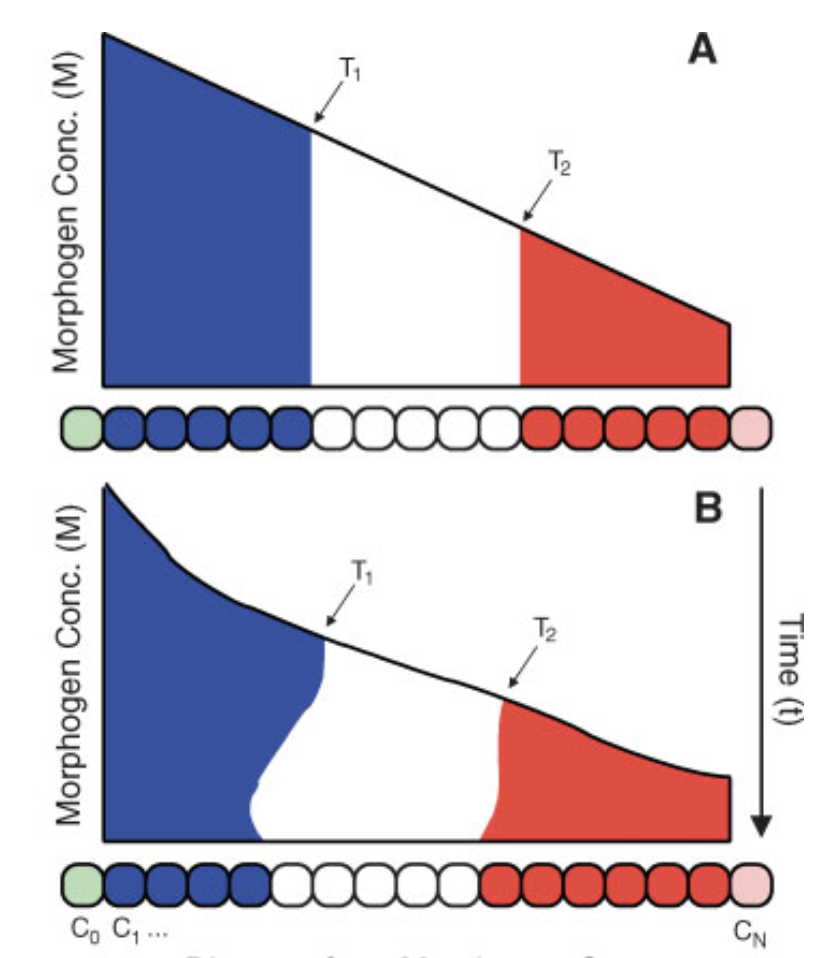
(1) How precisely does an interaction predict class-1 observations?

(2) How prevalent is an interaction among class-1 observations?

S = (x_{j_1} > t_{j_1}) \,\&\, \dots \,\&\, (x_{j_s} \le t_{j_s})
S=(xj1>tj1) & … & (xjs≤tjs)S = (x_{j_1} > t_{j_1}) \,\&\, \dots \,\&\, (x_{j_s} \le t_{j_s})

Interactions:

Responses:

y \in \{0, 1\}
y∈{0,1}y \in \{0, 1\}
r(\mathbf{x})=
r(x)=r(\mathbf{x})=

?

RuleFit: rule-based interaction discovery (Friedman and Popescu, 2008)

  1. Identify a collection of marginally important features
  2. Search for predictive order-2 rules among marginally important features
\dots
…\dots

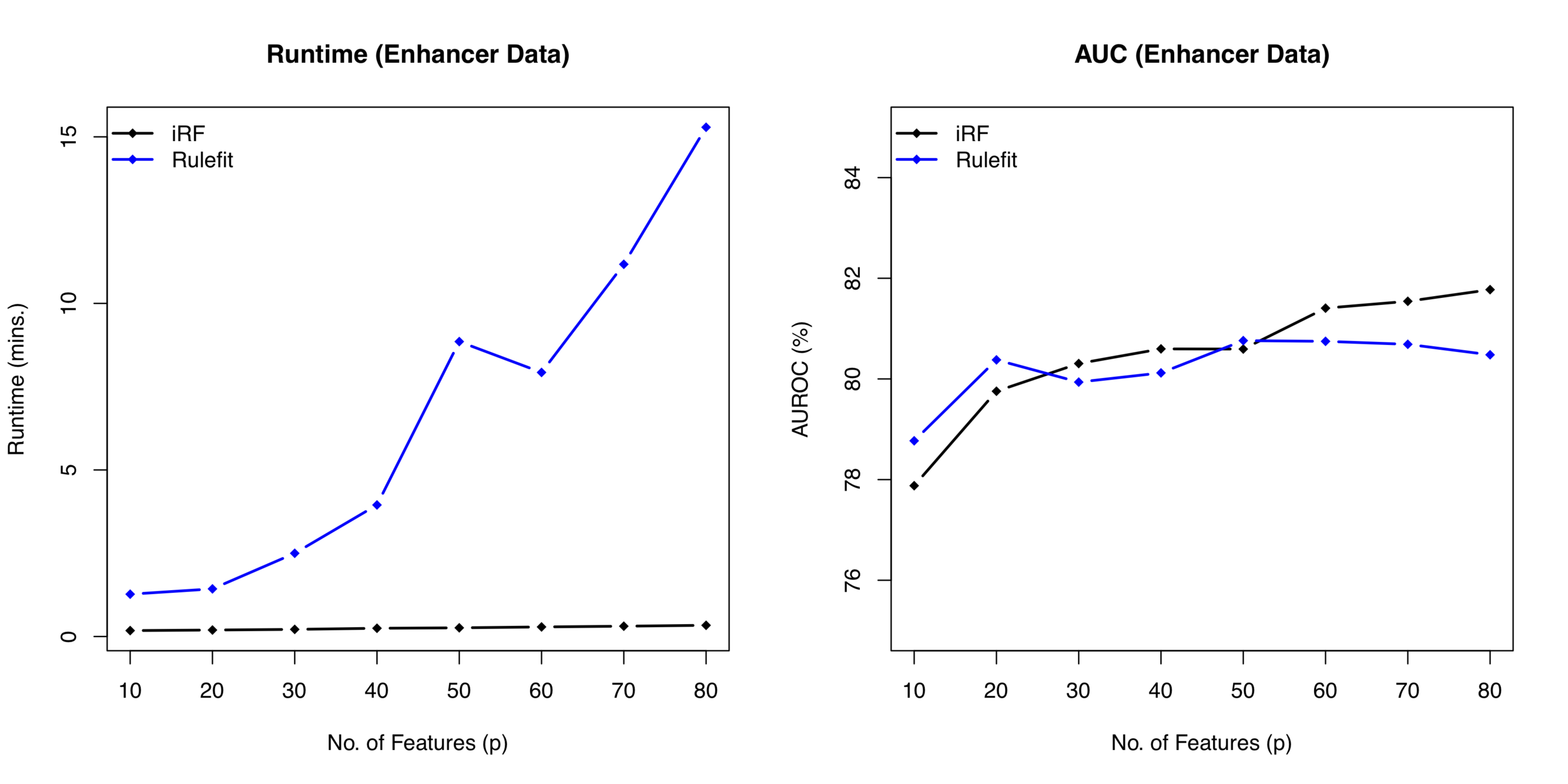
Computational costs grow as

O(p^s)
O(ps)O(p^s)

Misses interactions with weak  marginal effects

image: Lee and Haber (2014)

Market baskets and genomics 

Interactions in market baskets

What combinations of items do customers purchase together?

Interactions in market baskets

What combinations of items do customers purchase together?

What combinations of items do different types of customers purchase together?

Interactions in market baskets

Z_1
Z1Z_1
Z_2
Z2Z_2
Z_3
Z3Z_3
Z_4
Z4Z_4
\mathcal{I}_1
I1\mathcal{I}_1
\mathcal{I}_2
I2\mathcal{I}_2
\mathcal{I}_3
I3\mathcal{I}_3
\mathcal{I}_4
I4\mathcal{I}_4

Feature-index sets

Random intersection trees (RIT)

Shah and Meinshausen (2014)

Leverage sparsity in market baskets to search for frequently co-occurring items in a computationally efficient manner

  1. Randomly sample feature index sets from class-C observations:
  2.  Intersect sampled feature index sets in a tree like fashion up to depth D
  3. Return all feature combinations that "survive" intersection procedure up to depth D
\{\mathcal{I}_i \subseteq\{1, \dots, p\}: Z_i = C\}
{Ii⊆{1,…,p}:Zi=C}\{\mathcal{I}_i \subseteq\{1, \dots, p\}: Z_i = C\}

Random intersection trees (RIT)

Shah and Meinshausen (2014)

Randomly sampled

class-C observation

"survived" interaction

Random intersection trees (RIT)

Shah and Meinshausen (2014)

Random intersection trees (RIT)

Shah and Meinshausen (2014)

Genomic response

Genomic features

Translating the market basket problem into genomics

\dots
…\dots

Genomic response

Genomic features

Translating the market basket problem into genomics

Challenges:

  1. Genomic features are typically measured in concentrations/counts
  2. Binding does not imply regulation (Li et al. 2008)
\dots
…\dots

iterative Random Forests (iRF)

&

signed iterative Random Forests (s-iRF)

Joint work with Sumanta Basu, James B. Brown, Susan Celniker, and Bin Yu

 iterative Random Forest to identify high-order interactions in genomic data

  1. Iteratively re-weighted Random Forests stabilize decision path                       
  2. Generalized random intersection trees search for high-order interactions         
  3. Stability bagging evaluates interactions                           

iterative Random Forests (iRF) build on PCS to identify genomic interactions in developing Drosophila embryos 

Open source R implementation: https://cran.r-project.org/web/packages/iRF/

Iteratively re-weighted random forests

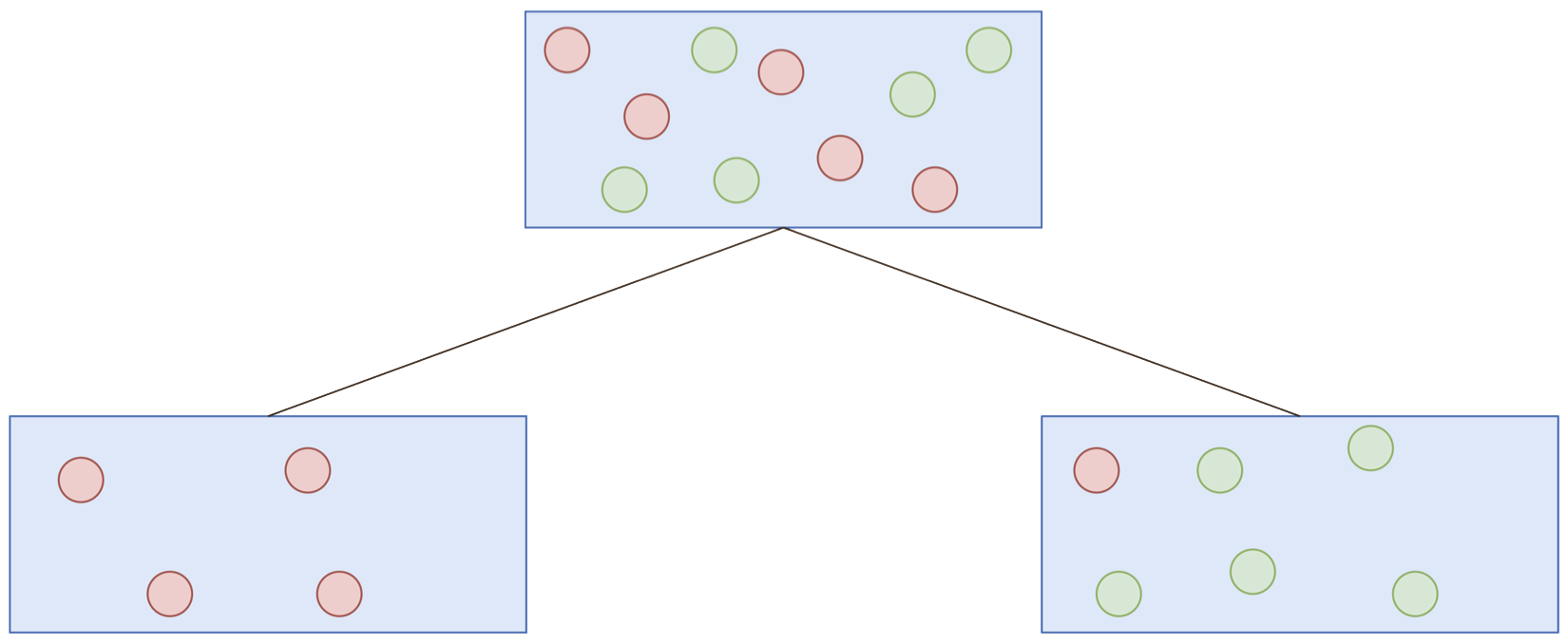
Classification and regression trees (CART)

Breiman et al. (1984)

 

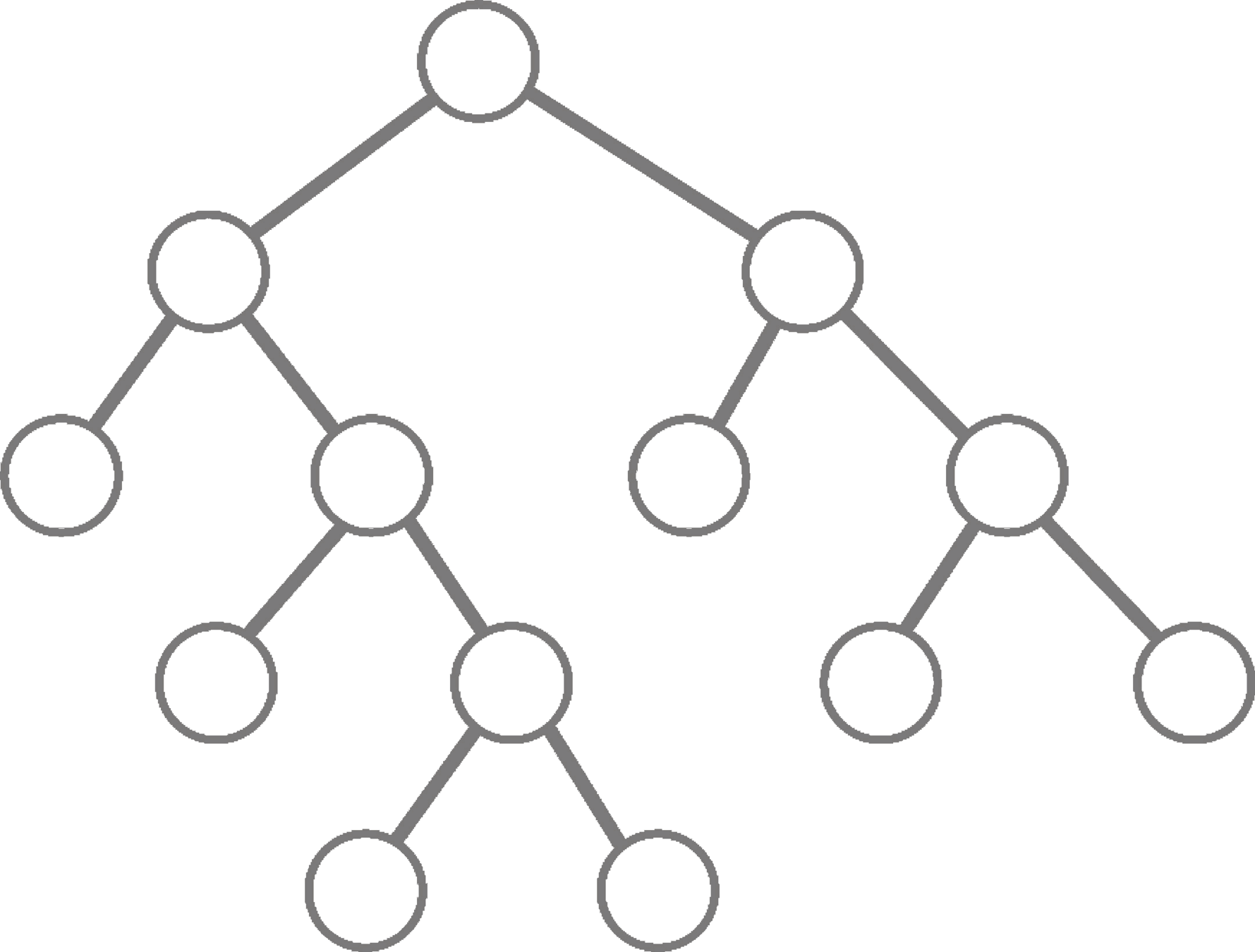
For current node:

  1. Select splitting feature and threshold
  2. Partition data 
  3. Repeat until stopping criteria
x_2>t_2
x2>t2x_2>t_2
x_3>t_3
x3>t3x_3>t_3
x_4>t_4
x4>t4x_4>t_4

Classification and regression trees (CART)

Breiman et al. (1984)

 

For current node:

  1. Select splitting feature and threshold
  2. Partition data 
  3. Repeat until stopping criteria
x_2>t_2
x2>t2x_2>t_2
x_3>t_3
x3>t3x_3>t_3
x_4>t_4
x4>t4x_4>t_4
(x_2 > t_2) \,\&\,(x_3 > t_3) \,\&\,(x_4 > t_4)
(x2>t2) & (x3>t3) & (x4>t4)(x_2 > t_2) \,\&\,(x_3 > t_3) \,\&\,(x_4 > t_4)

The CART criterion: Gini impurity

(\pi, N)
(π,N)(\pi, N)
(\pi_l, N_l)
(πl,Nl)(\pi_l, N_l)
(\pi_r, N_r)
(πr,Nr)(\pi_r, N_r)

Proportion positive responses

Number of observations

Gini impurity:

I_G(\pi) = \pi (1-\pi)
IG(π)=π(1−π)I_G(\pi) = \pi (1-\pi)

Decrease in Gini impurity:

I_G(\pi)-\frac{N_l}{N}I_G(\pi_l) - \frac{N_r}{N}I_G(\pi_r)
IG(π)−NlNIG(πl)−NrNIG(πr)I_G(\pi)-\frac{N_l}{N}I_G(\pi_l) - \frac{N_r}{N}I_G(\pi_r)

Mean decrease in impurity:

On average, how much does splitting on a variable decrease the Gini impurity?

Random Forests

Breiman (2001)

Random forests modify CART to improve predictive accuracy:

  1. CART trees are trained on bootstrap samples of the data
  2. CART criterion evaluated on subset of features sampled uniformly at random

Feature-weighted Random Forests

Amaratunga et al. (2008)

Random forests: 

At each node of the decision tree, uniformly sample a subset of features

Feature-weighted random forests: 

At each node of the decision tree, sample a subset of features with probability proportional to 

w\in\mathbb{R}^p_+
w∈R+pw\in\mathbb{R}^p_+
w_1
w1w_1
w_2
w2w_2
w_3
w3w_3
w_4
w4w_4
w_5
w5w_5
w_1
w1w_1
w_2
w2w_2
w_3
w3w_3
w_4
w4w_4
w_5
w5w_5

Feature weights

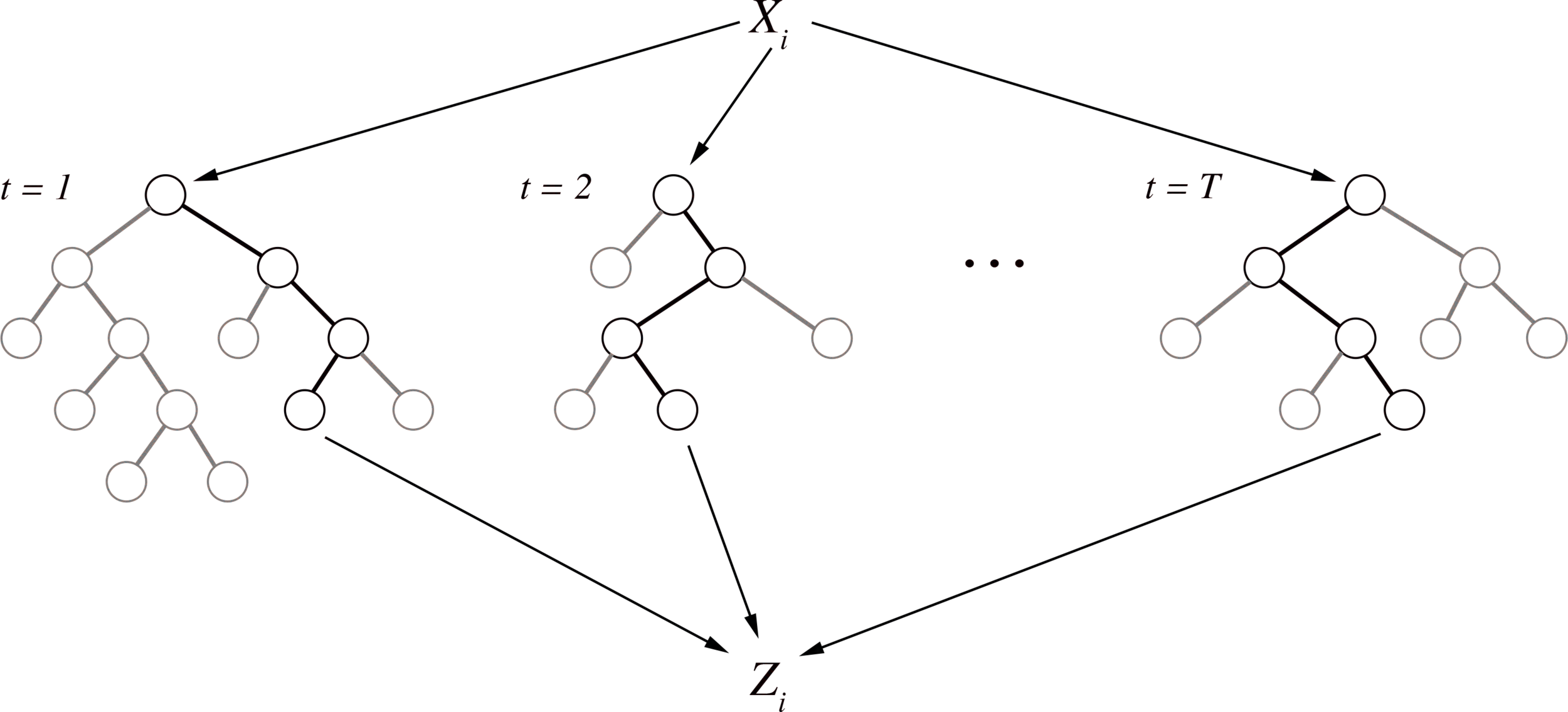
Iterative re-weighting stabilizes random forest decision paths

Gini importance

Iteration 1

Iteration K

w_1
w1w_1
w_2
w2w_2
w_3
w3w_3
w_4
w4w_4
w_5
w5w_5
w_1
w1w_1
w_2
w2w_2
w_3
w3w_3
w_4
w4w_4
w_5
w5w_5

Feature weights

Iterative re-weighting helps recover high-order interactions

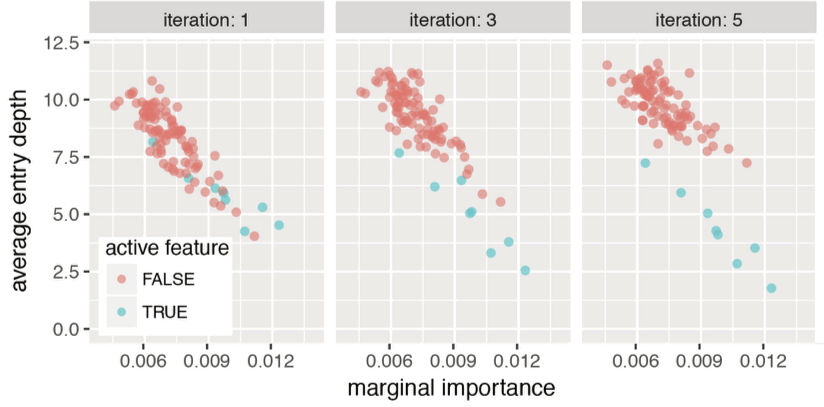
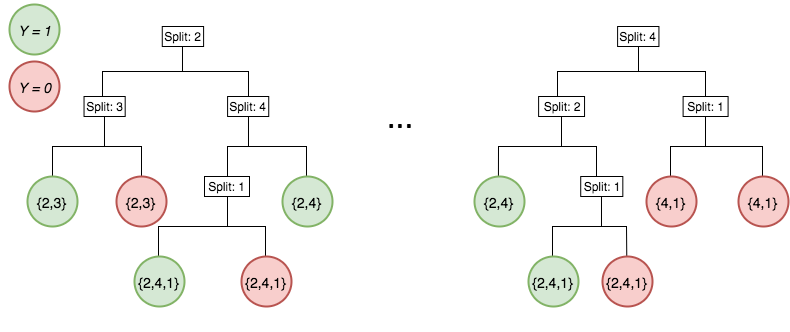
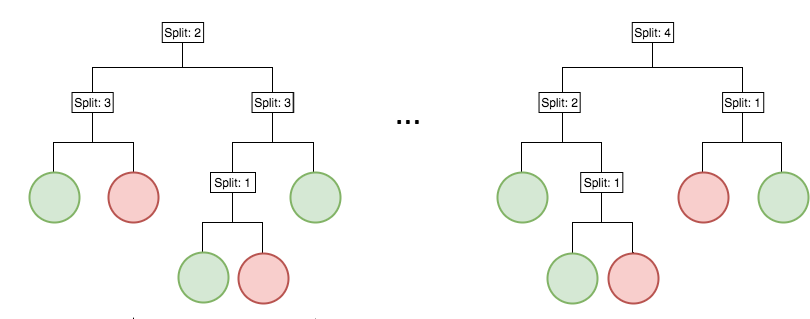
Generalized random intersection trees

Encoding decision paths to extract active features

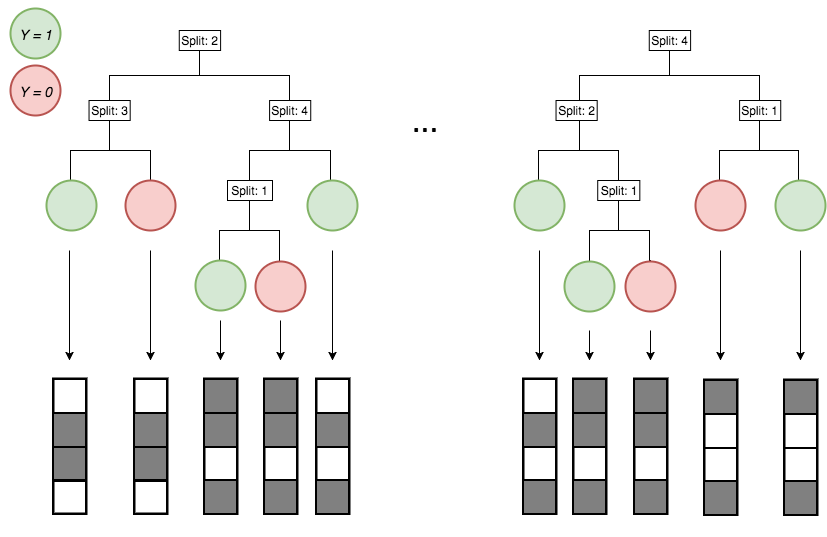
Active

Inactive

Continuous measurements

Binary features

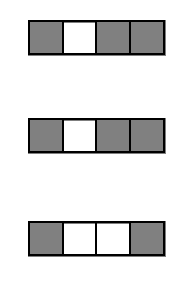
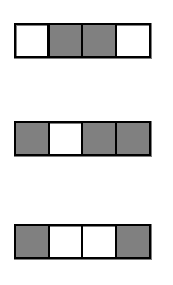
Encoding decision paths to extract enriched and depleted features

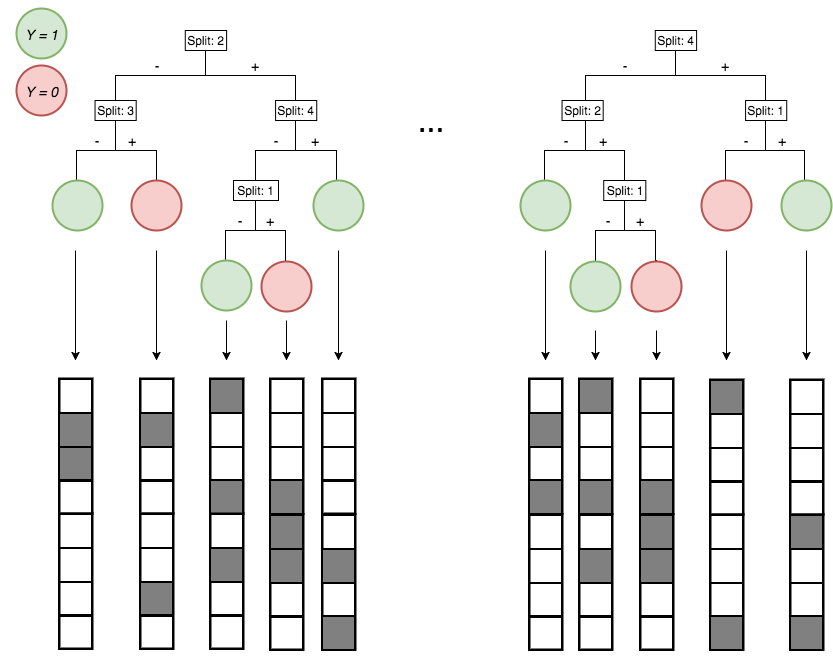
Enriched

Depleted

Generalized random intersection trees search for high-order interactions

\cap
∩\cap
\cap
∩\cap
\cap
∩\cap
\cap
∩\cap
\{1,4\}
{1,4}\{1,4\}

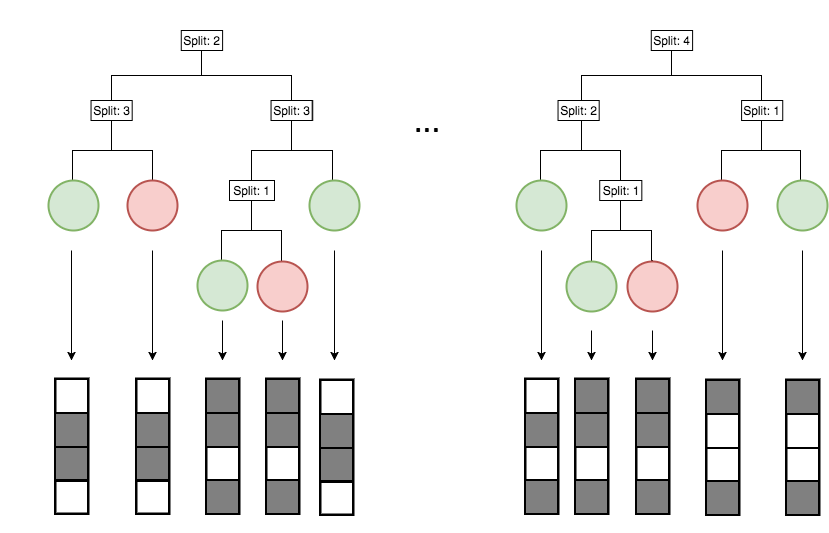
1. Iteratively re-weighted random forests

3. RIT on random forest decision paths

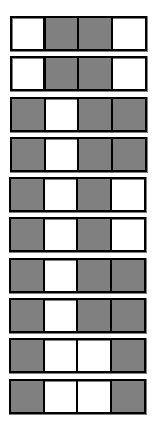
2. Decision path feature transformation

\mathbf{x}_1 \rightarrow \mathcal{I}_1 =
x1→I1=\mathbf{x}_1 \rightarrow \mathcal{I}_1 =
\mathbf{x}_n \rightarrow \mathcal{I}_n =
xn→In=\mathbf{x}_n \rightarrow \mathcal{I}_n =

.

.

.

\emptyset
∅\emptyset

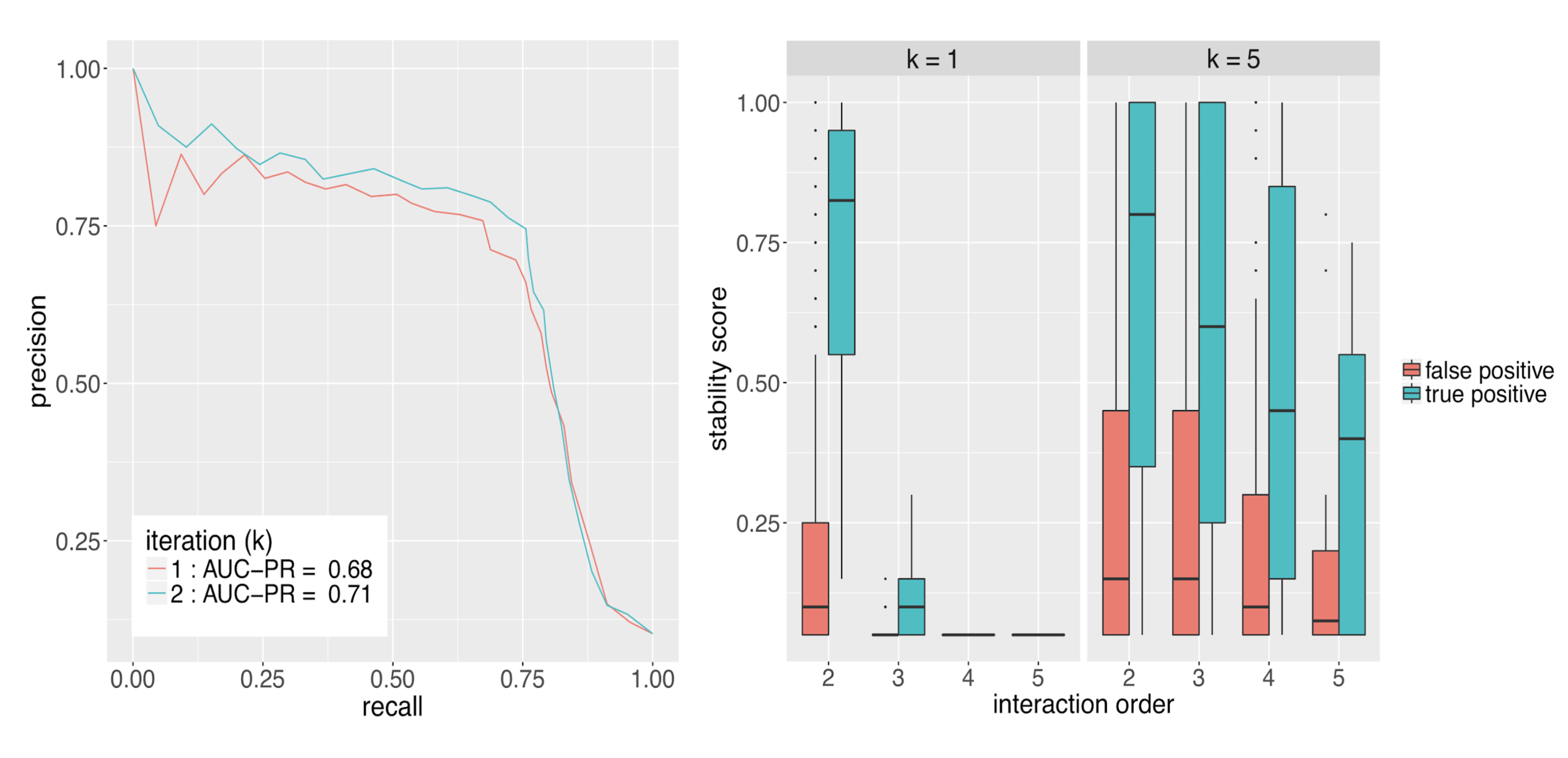
Runtime comparison between iRF and RuleFit

Evaluating interactions

Summary of importance measures for high-order interactions

Importance measures:

  1. Prevalence              : how frequently is an interaction observed among positive responses?
  2. Precision              : how accurately does an interaction predict positive responses?

 

Null importance measures:

  1. Class enrichment: is an interaction more prevalent among a particular class?
  2. Interaction strength: is feature selection dependent on the joint distribution of features?
  3. Minimal representation: how much do additional features improve prediction accuracy?
P(S|C)
P(S∣C)P(S|C)
P(C|S)
P(C∣S)P(C|S)

Prevalence measures the stability of an interaction across an RF

Prevalence: 

P(S|y=1)=\frac{1}{T} \sum_{t=1}^T \frac{\sum_{i=1}^n I(S\subseteq \mathcal{I}_{i_t}) \cdot I(y_i = 1)}{\sum_{i=1}^n I(y_i = 1)}
P(S∣y=1)=1T∑t=1T∑i=1nI(S⊆Iit)⋅I(yi=1)∑i=1nI(yi=1)P(S|y=1)=\frac{1}{T} \sum_{t=1}^T \frac{\sum_{i=1}^n I(S\subseteq \mathcal{I}_{i_t}) \cdot I(y_i = 1)}{\sum_{i=1}^n I(y_i = 1)}
P(\{1, 3, 4\}|y = 1) =3/5
P({1,3,4}∣y=1)=3/5P(\{1, 3, 4\}|y = 1) =3/5
P(\{1, 4\}|y = 1) =4/5
P({1,4}∣y=1)=4/5P(\{1, 4\}|y = 1) =4/5

Examples:

Precision measures the predictive accuracy of an interaction across an RF

Precision:

P(y=1|S)=\frac{1}{T} \sum_{t=1}^T \frac{\sum_{i=1}^n I(S\subseteq \mathcal{I}_{i_t}) \cdot I(y_i = 1)}{\sum_{i=1}^n I(S\subseteq \mathcal{I}_{i_t})}
P(y=1∣S)=1T∑t=1T∑i=1nI(S⊆Iit)⋅I(yi=1)∑i=1nI(S⊆Iit)P(y=1|S)=\frac{1}{T} \sum_{t=1}^T \frac{\sum_{i=1}^n I(S\subseteq \mathcal{I}_{i_t}) \cdot I(y_i = 1)}{\sum_{i=1}^n I(S\subseteq \mathcal{I}_{i_t})}
P(y=1|\{1, 4\}) = 4/6
P(y=1∣{1,4})=4/6P(y=1|\{1, 4\}) = 4/6
P(y=1|\{1, 3, 4\}) = 3/4
P(y=1∣{1,3,4})=3/4P(y=1|\{1, 3, 4\}) = 3/4

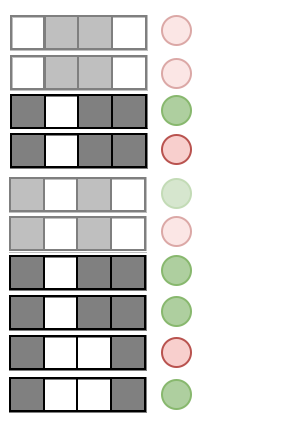
Examples:

Bagging evaluates stability of interactions across entire iRF workflow relative to resampling

\cap
∩\cap
\cap
∩\cap
\cap
∩\cap
\cap
∩\cap
\cap
∩\cap
\cap
∩\cap
\cap
∩\cap
\cap
∩\cap
\{1,4\}
{1,4}\{1,4\}
\{1,3\}
{1,3}\{1,3\}
P(S|y=1)
P(S∣y=1)P(S|y=1)
P(S|y=1)
P(S∣y=1)P(S|y=1)
\dots
…\dots

1. Iteratively re-weighted RF stabilize decision paths

2. gRIT searches for high-order interactions along decision paths

3. Importance metrics evaluate interactions in fitted RF

Outer layer bootstrap samples

\emptyset
∅\emptyset
\{1,4\}
{1,4}\{1,4\}

Case studies in Drosophila

Predicting enhancer activity in early stage Drosophila embryos

Enhancers: Pfeiffer et al. 2008, Fisher et al. 2012, Kvon et al. 2014

ChIP: MacArthur et al. 2009, Li et al. 2008

  • 7809 loci representing ~14% of the non-coding genome
  •    : 24 TF ChIP assays, stage 4-6 blastoderm embryos
  •    : enhancer activity (0: inactive, 1: active)
\mathbf{x}
x\mathbf{x}
y
yy
x_1
x1x_1
x_2
x2x_2
\dots
…\dots
y
yy

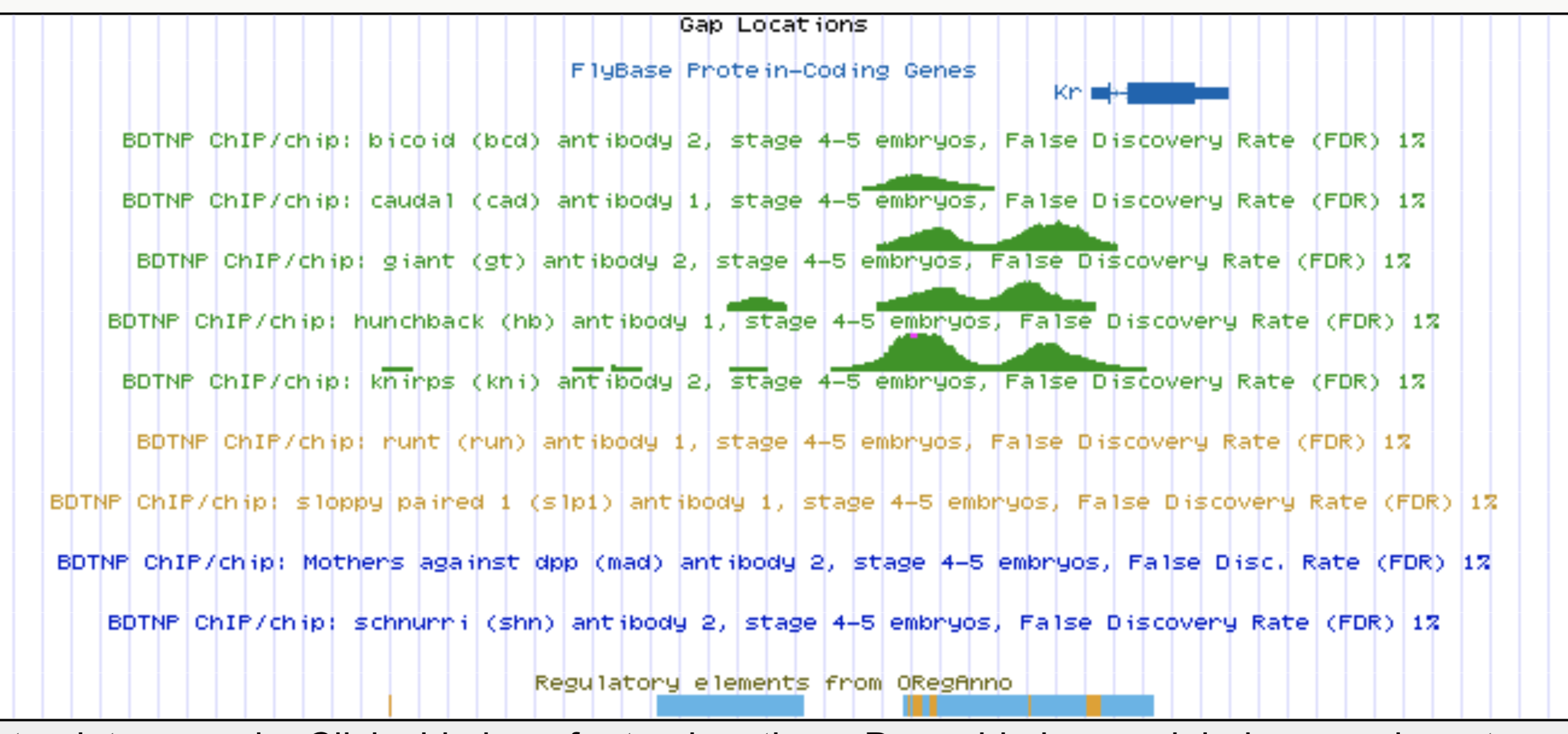
Predicting enhancer activity in early stage Drosophila embryos

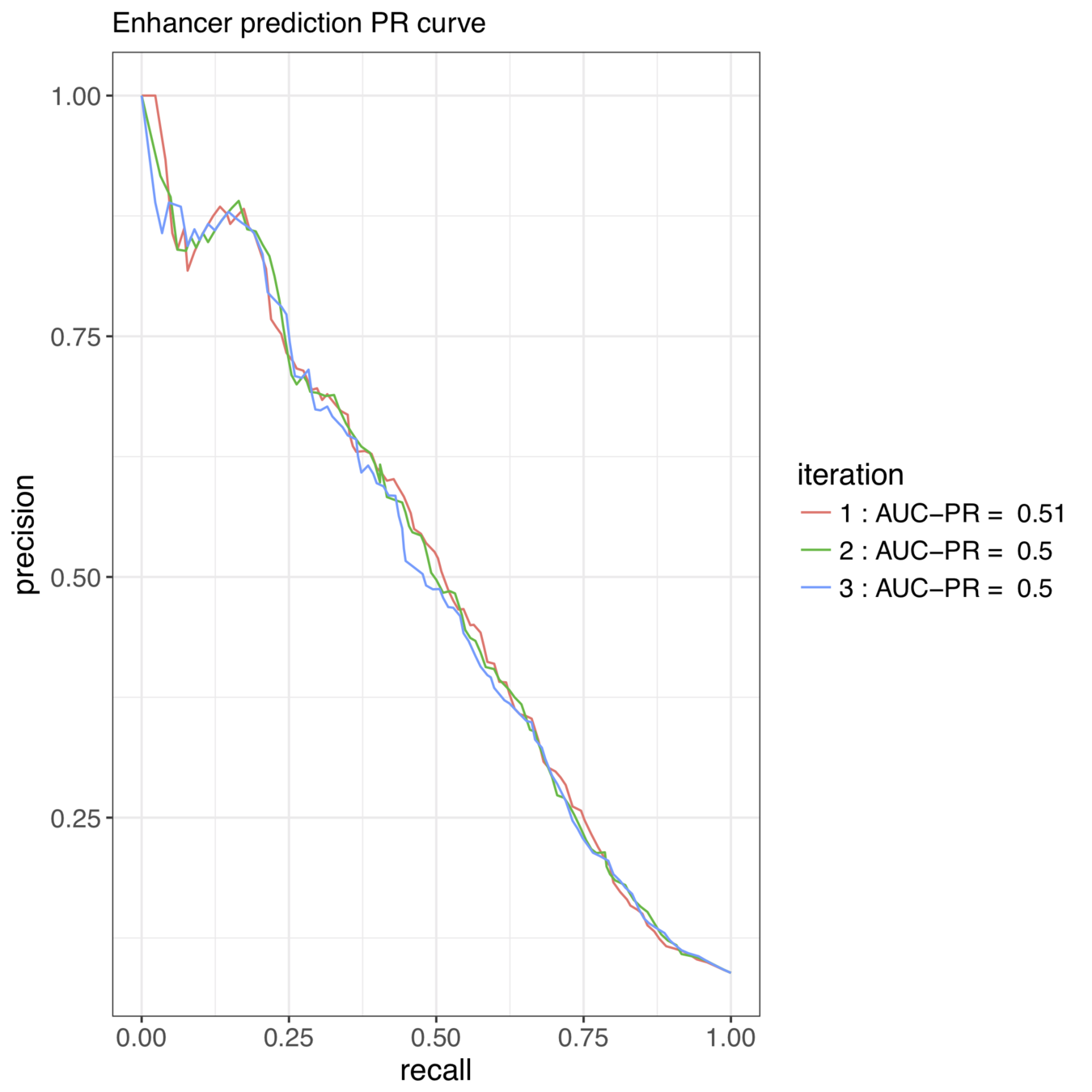
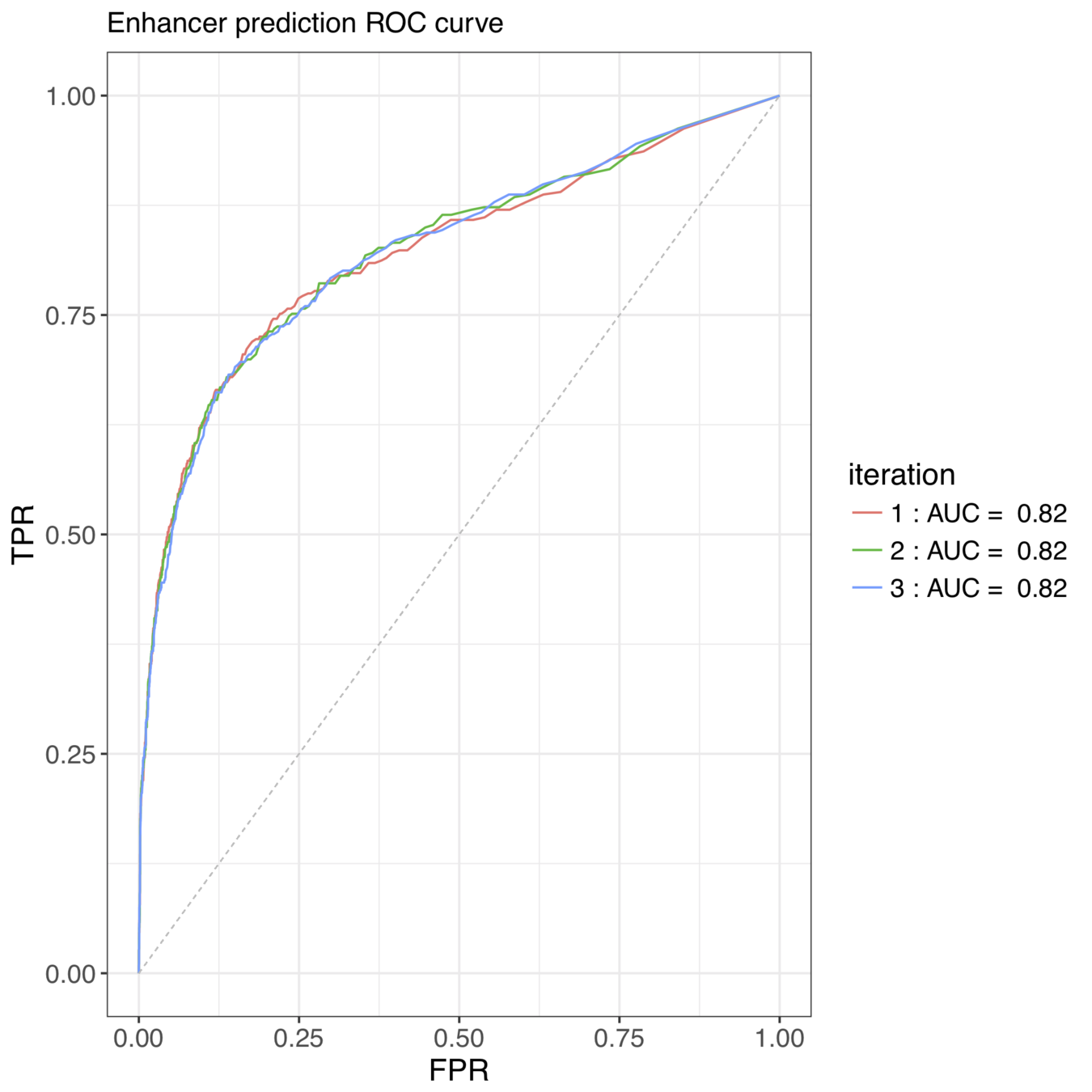
iterative Random Forests recover well-known pairwise interactions

Accurately predicted enhancer elements correspond to A-P expression patterns

active enhancer

Rule predicted probability

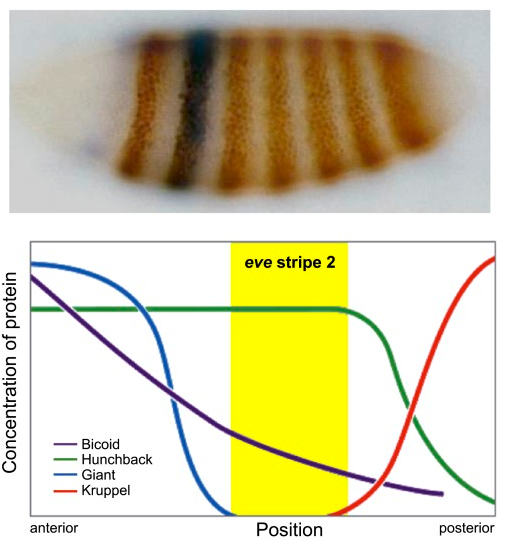
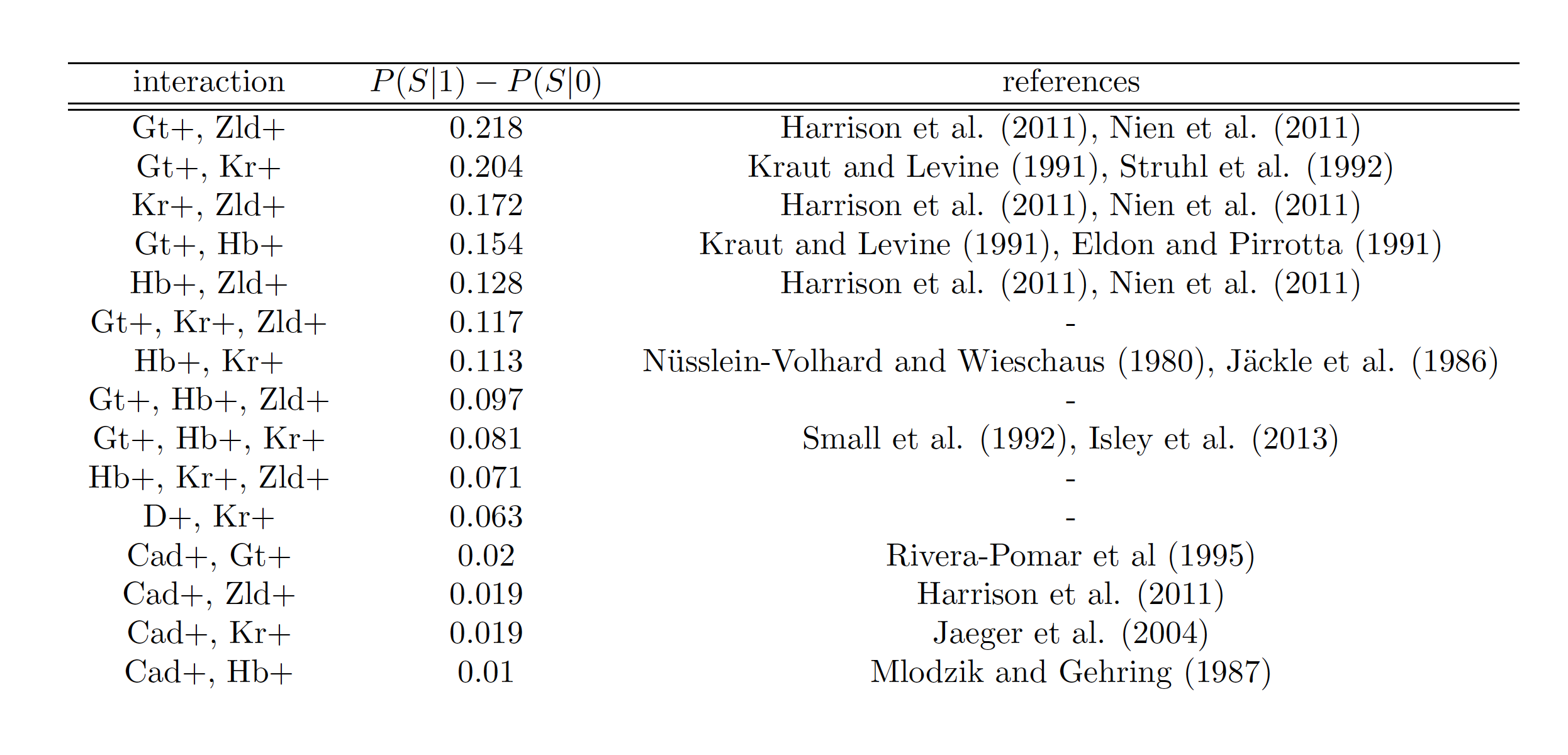
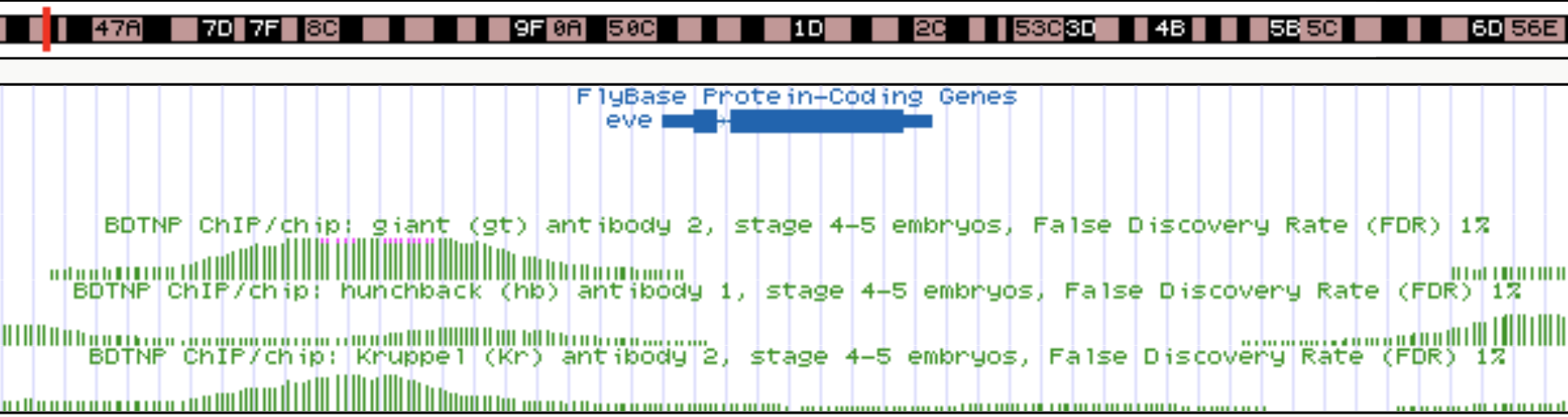
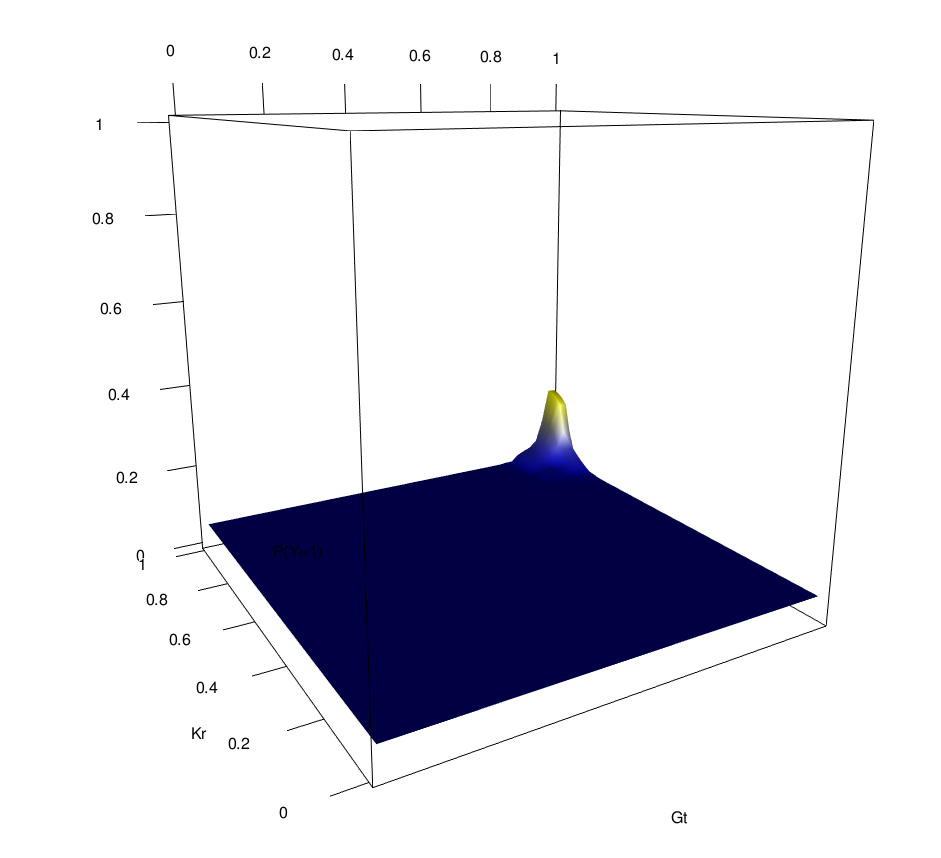
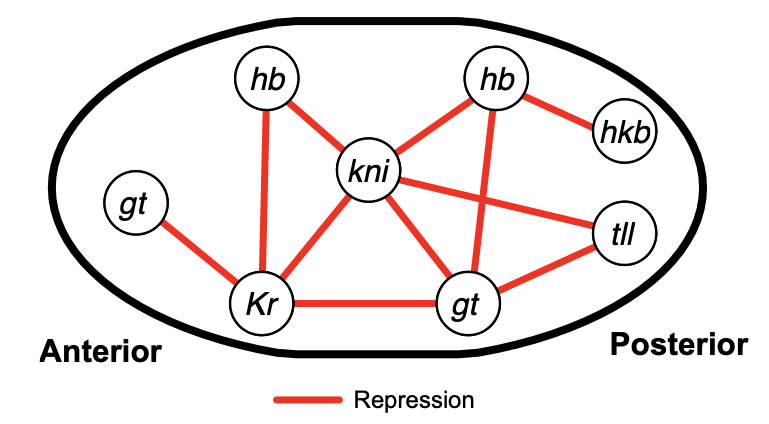
s-iRF identifies known target of order-3 gap gene interaction

Known target of order-3 interaction among Gt, Kr, and Hb

Gt

Kr

Hb

eve

Gt, Kr, Hb binding

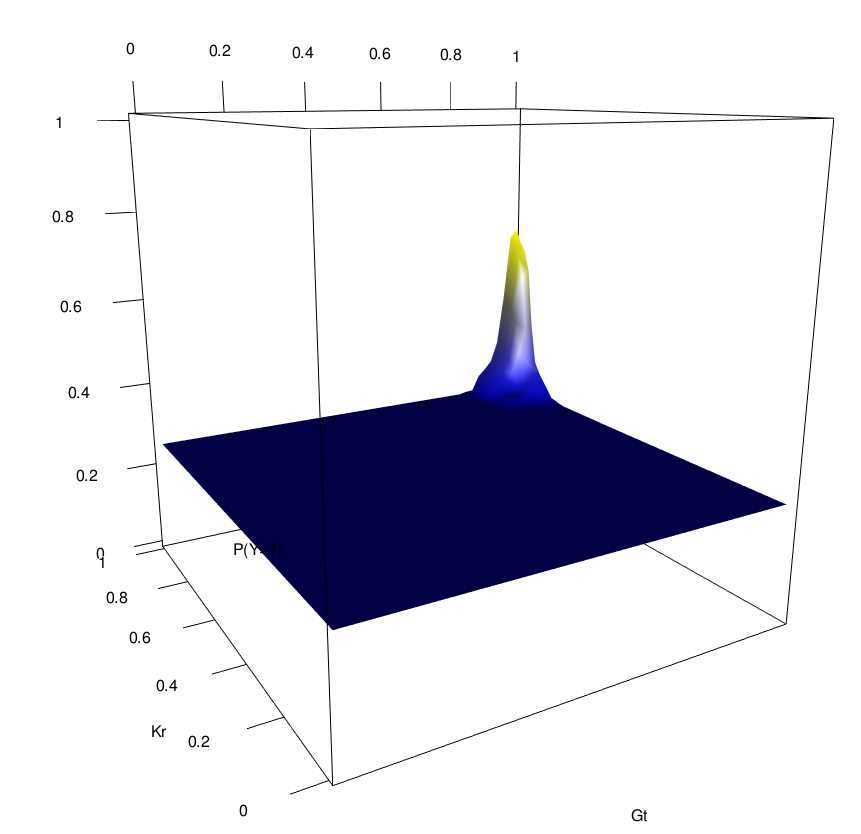
s-iRF suggests novel targets for order-3 gap gene interaction

Gt, Kr, Hb

binding

Known gap gene target

Kni

Gt

Kr

Hb

s-iRF suggests novel targets for order-3 gap gene interaction

Gt, Kr, Hb

binding

Known gap gene target

Gt

Kr

Hb

Cad early

Cad late

Novel order-3 interactions exhibit AND-like behavior (Hb, Kr, Zld)

P(y=1)
P(y=1)P(y=1)

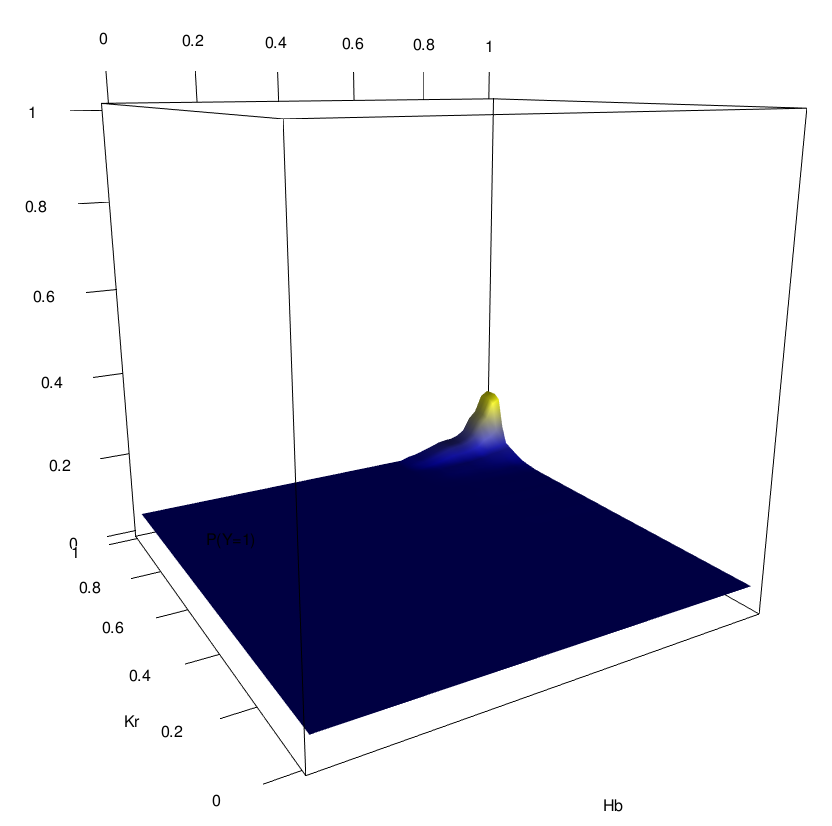
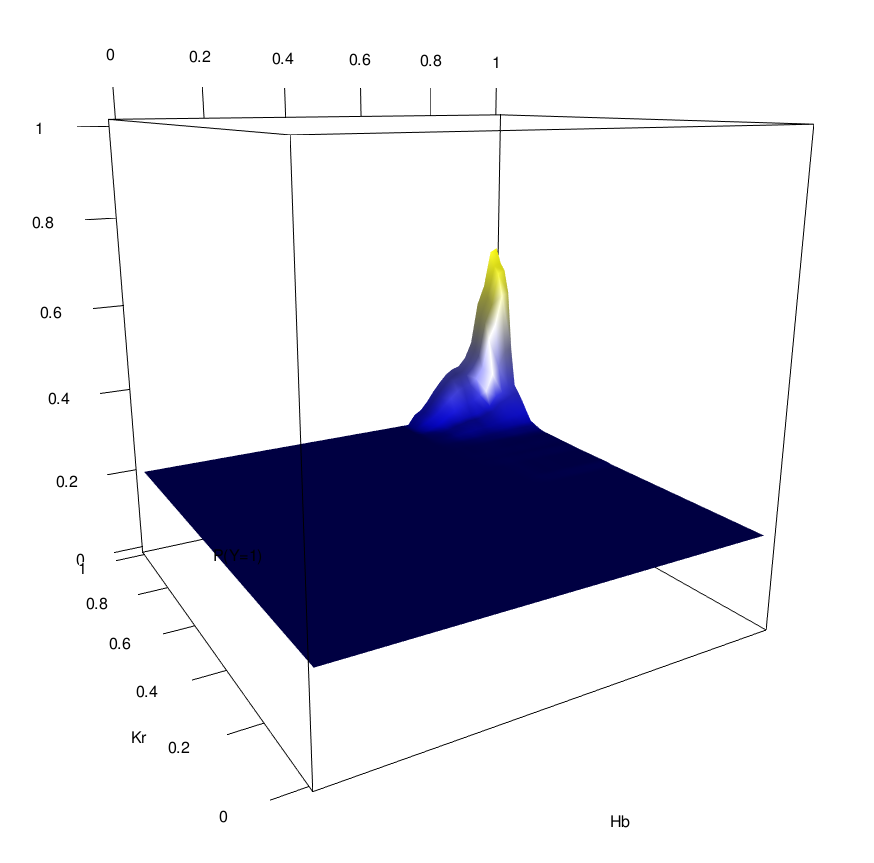
Zld low

Zld high

Hb

Kr

Kr

Hb

Novel order-3 interactions exhibit AND-like behavior (Gt, Kr, Zld)

P(y=1)
P(y=1)P(y=1)

Zld low

Zld high

Gt

Kr

Kr

Gt

Identifying regulatory interactions from high-throughput spatial expression data

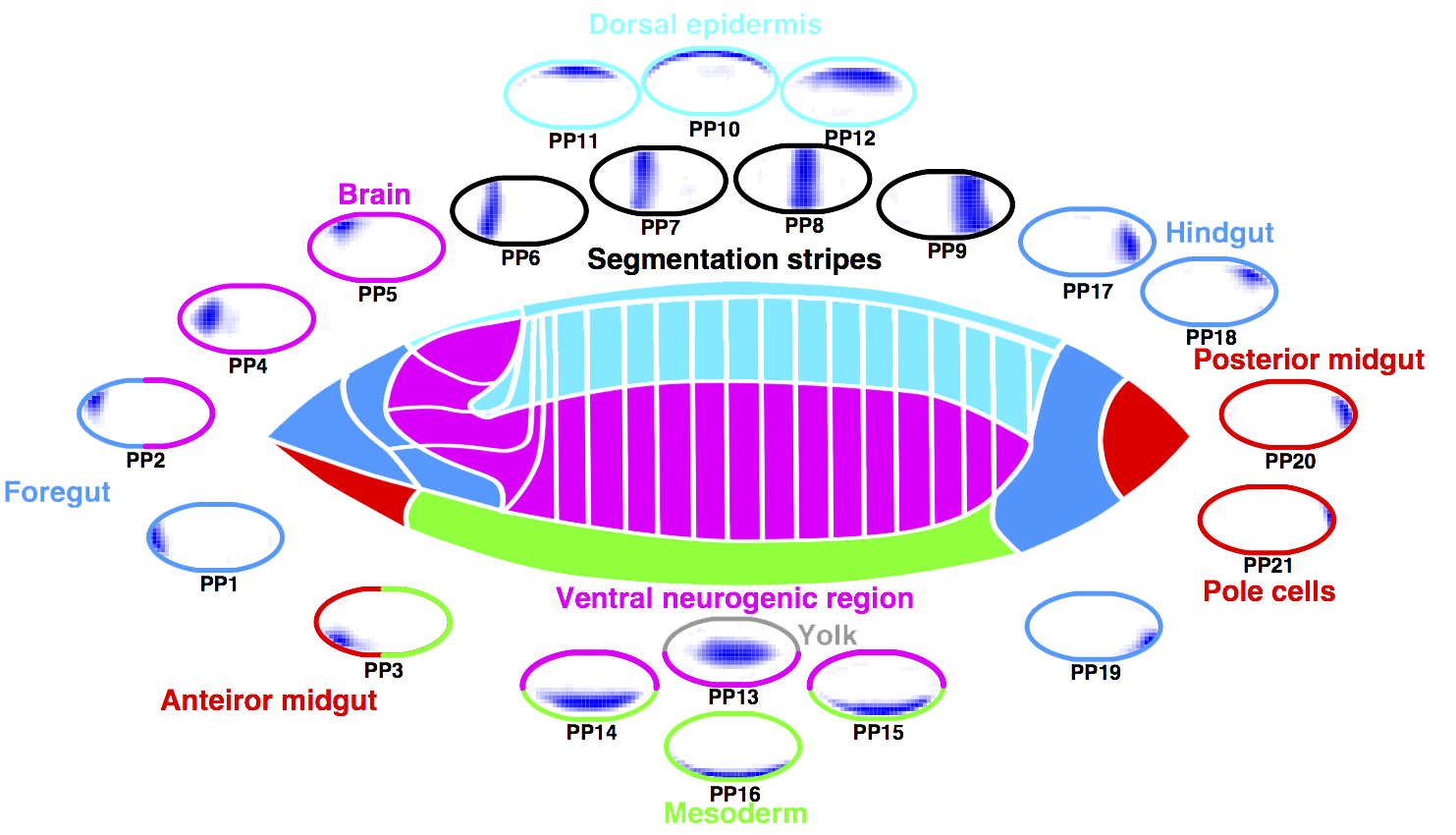
Berkeley Drosophila Genome Project:

TF spatial gene expression patterns

Pre-organ region principal patterns (PP)

Wu et al. (2016)

Predicting spatial gene expression patterns in early stage Drosophila embryos

Detection and registration

Registered

images

Stain

extraction

Data: Wu et al. (2016)

  • 405 pixels (~7 cells)
  •    : 22 TF gene expression patterns
  •    : 5 anterior-posterior PPs
\mathbf{x}
x\mathbf{x}
y
yy

Principal patterns (PP)

From genomic to statistical interactions: spatial expression

+
++
+
++
+
++
\dots\approx
⋯≈\dots\approx
\dots
…\dots
r(\mathbf{x})=
r(x)=r(\mathbf{x})=
\prod_{j\in\text{A}} 1(x_j > t_j)
∏j∈A1(xj>tj)\prod_{j\in\text{A}} 1(x_j > t_j)
\cdot
⋅\cdot
\prod_{j\in\text{R}} 1(x_j \le t_j)
∏j∈R1(xj≤tj)\prod_{j\in\text{R}} 1(x_j \le t_j)

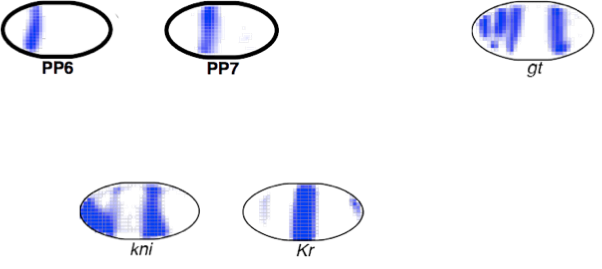
activators

repressors

PP7 expression rule

\mathbf{x}=(x_1, \dots, x_p)
x=(x1,…,xp)\mathbf{x}=(x_1, \dots, x_p)

Region of the embryo

Expression levels of p transcription factors (TFs)

Test case: the gap gene network

Fruitfly embryo segmentation

Human embryo segmentation

Nobel Prize in Physiology or Medicine 1995

Edward B. Lewis, Christiane Nusslein-Volhard, Eric F. Wieschaus

Predicting spatial gene expression patterns in early stage Drosophila embryos

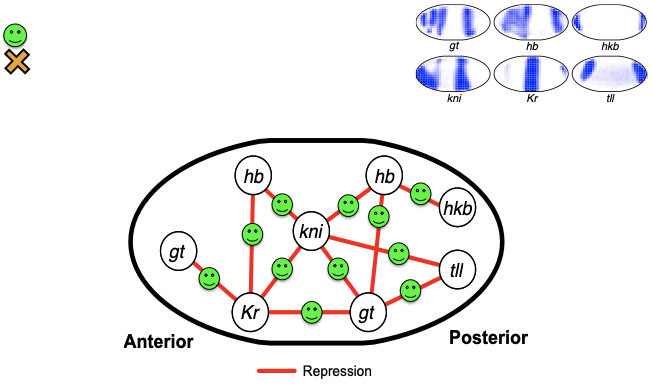
: interactions correctly predicted

: interactions missed

PP17 interactions

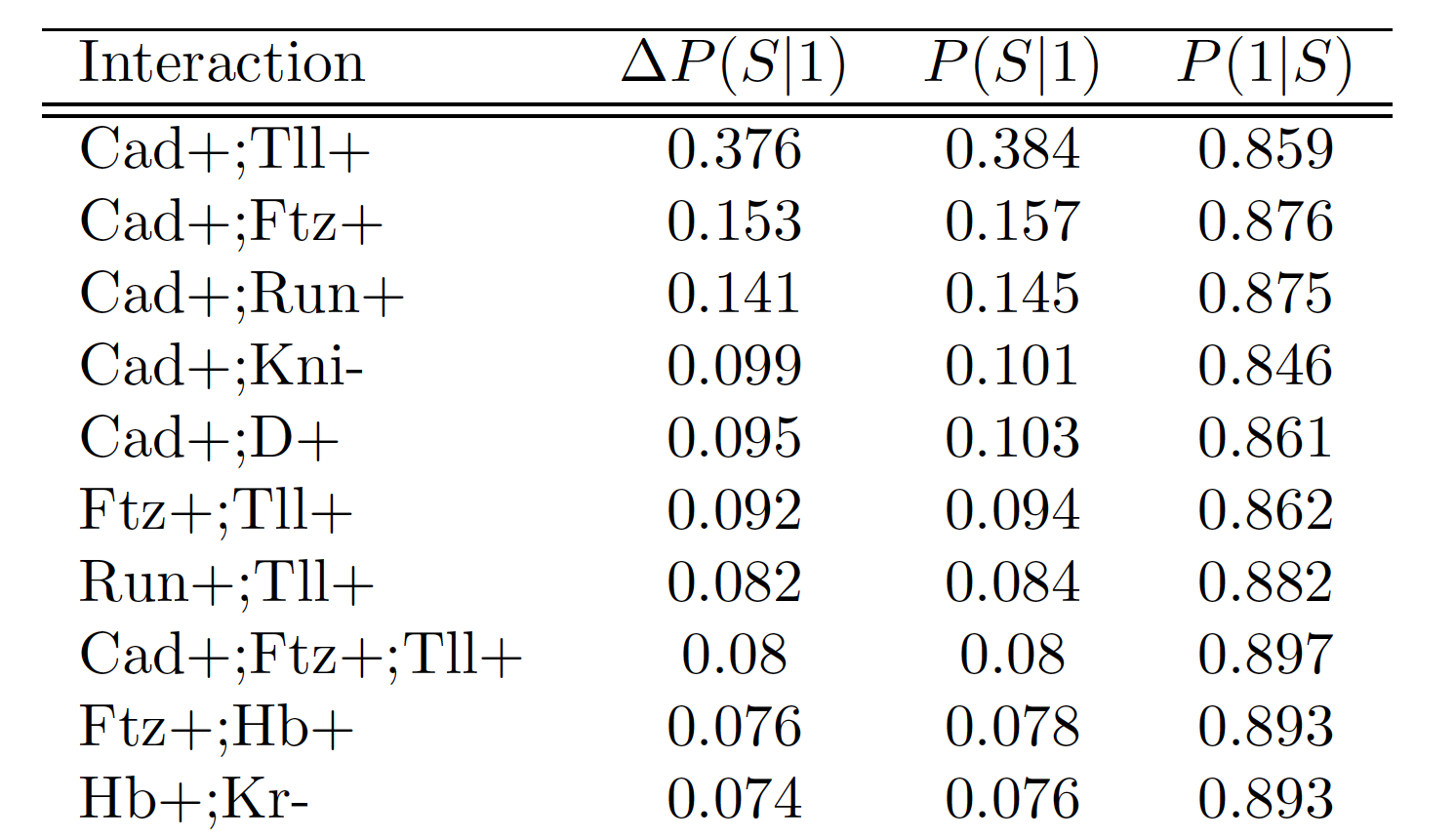
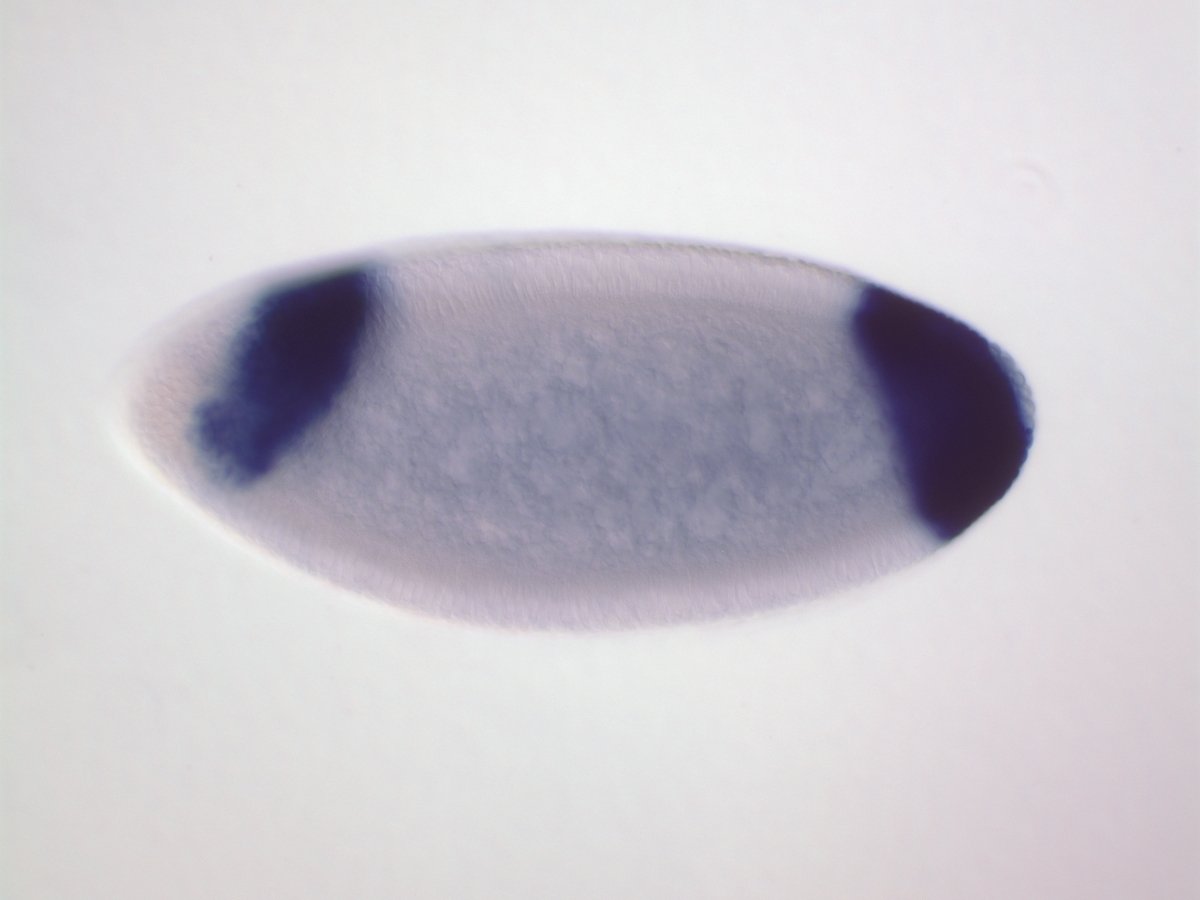
Cad

Tll

Ftz

Interactions recovered in spatial expression data co-bind at enhancer elements

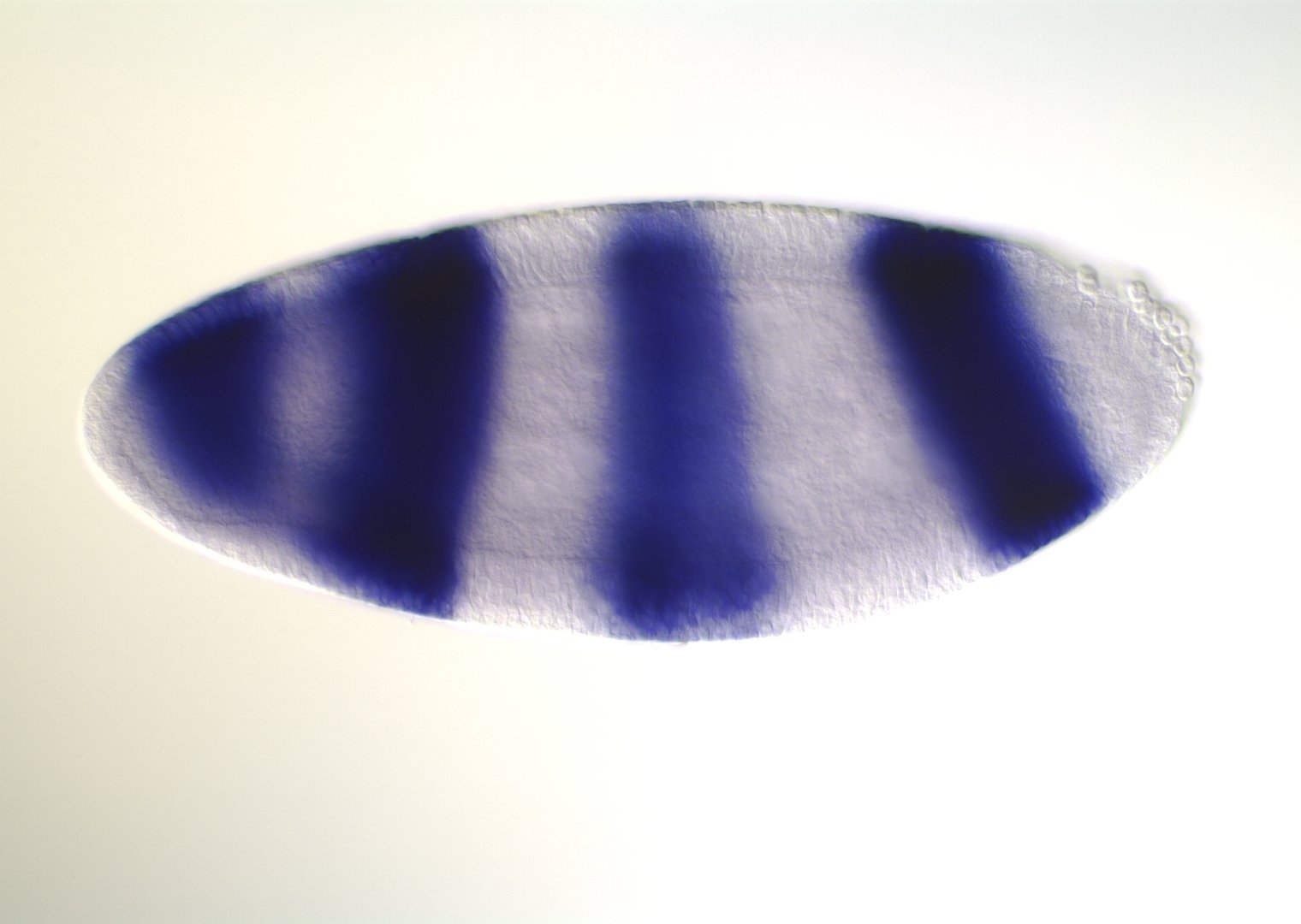
Blimp-1

Cad

Tll

Ftz

Cad, Tll, Ftz

binding

Interactions recovered in spatial expression data co-bind at enhancer elements

h

Cad

Tll

Ftz

Cad, Tll, Ftz

binding

Summary

  • iRF and s-iRF identify well known interactions in Drosophila and posit new, high-order interactions surrounding important regulatory factors in the early embryo. 
  • By decoupling interaction order from the computational cost of discovery, iRF and s-iRF allow us to investigate mechanisms in genome biology and beyond (King et al., 2018; Long et al. 2018)

Other PhD projects

  • PCS inference for ML models/algorithms

         Joint with: Bin Yu

  • Decoding spatial gene expression patterns in late stage Drosophila embryos

         Joint with: Runjing Liu, Erwin Frise, Susan Celniker, Bin Yu

  • Evaluating interpretability in ML models/algorithms

         Joint with: Reza Abbasi Asl, Jamie Murdoch, Chandan Singh, and               Bin Yu

Future work

  • Investigating and characterizing emergent phenomena in biological systems, with a focus on disease states (e.g. neurodegeneration)
  1. Extracting localized interactions from ML models
  2. Incorporating dependencies into ML models
  3. Building mechanistic constraints/experimental results into ML models
  1. Characterizing mechanisms in heterogeneous cell populations
  2. Capturing dynamics of cellular behavior/responses
  3. Exploring how mechanistic insights inform treatment strategies

Biological challenges

Statistical challenges

Ackowledgements

S. Basu

J. Brown

B. Yu

S. Celniker

E. Frise

Made with Slides.com