競技プログラミング練習会

2020 Normal

第７回　グラフ表現,構造体, Union-Find木

担当 :  zeke

自己紹介

自己紹介

  • 京都大学工学部手書きレポート学科2回生
  • 本名：岡島 和希
  • C++を普段使ってます。そろそろPython使えるようになりたい
  • コドゲでは426位でした、もう少し伸ばしたかった…
  • 暇なのでKaggleなどを始めた

KMC-ID:zeke

今日の内容

今日の内容

  • グラフとは
  • グラフ表現
    • 隣接リスト
    • 隣接行列
  • Union-Find 木

グラフ理論is何?

グラフとは

  • グラフっていうと、思い浮かべるのは棒グラフ,折れ線グラフ,etcだと思う。
  • 今日やるのは、それとは全然違います！！

グラフとは(概要)

  • グラフ理論というのがあります。
  • そこで言うグラフは、2次元上の頂点同士を辺で結んだ図のこと。
  • 競プロでのグラフは主にこっち

こんなの→

現実のグラフの例

  • 都市とそれらを結ぶ道
  • 島と航路
  • 駅と路線
  • SNSの交友関係
  • ゲーム理論の局面遷移
  • 抽象グラフ(ex:動的計画法)
  • …

現実のグラフの問題例

  • 最短距離問題
  • 最小全域木問題
  • 巡回セールスマン問題
  • ネットワークフロー問題
  • 安定マッチング問題
  • 中国人郵便配達問題
  • 幾何彩色問題
  • …

応用範囲が大きい！

グラフ理論

目次：グラフ理論(リンク付き)

定義

辺の向き(有向グラフ,無向グラフ)

部分グラフ(,全域部分グラフ)

隣接

完全グラフ

特殊な辺(ループ,多重辺)

次数(入次数,出次数)

道(,閉路,距離)

(橋,)木,根つき木

連結(,連結成分)

グラフの定義

  • 集合V : 頂点(vertex), 節点(node)
  • 集合E : 辺(edge),枝,(弧)
    • \(E\subset \{(x,y)\in V\times V\}\)
      • \((x,y)\in E\) は頂点xとyを結ぶ辺。
      • 要はEは二頂点の集合ってこと。
  • 図で描くときはさっきみたいに丸(or四角)を線分か矢印で繋ぐ。
  • グラフは集合G=(V,E)として表せる(集合の集合)
  • これからグラフでよく出てくる用語の説明をします

ひたすら知識を伝えていきますが、

知っておくといいことがあるかもです

グラフの例

  • V={1,2,3,4,5}
  • E={(1,2),(1,4),(2,3),(2,4),(2,5),(3,4),(4,5)}

辺の向き

  • 有向グラフ
    • 辺に向きがあるグラフ。
    • 図では辺を矢印で表現。
  • 無向グラフ
    • 辺に向きがないグラフ。
    • 図では辺を線分で表現。
    • さっきまでのグラフはこっち。

有向グラフ

無向グラフ

部分グラフ

  • 部分グラフ
    • 元のグラフからいくつかの頂点といくつかの辺を取ってきたグラフ
      • \(G'=(V',E'),V'\subset V,E'\subset E\)
  • 全域部分グラフ
    • 元のグラフから全ての頂点といくつかの辺を取ってきたグラフ
      • \(G'=(V,E'),E'\subset E\)

G=(V,E)

隣接

  • 隣接
    • uとvが辺で繋がっている時、「頂点u,vは隣接している」と言う
      • \((u,v)\in E\)
  • 頂点vの隣接点
    • vと隣接してる頂点
    • \((u,v)\in E\)のとき、uとvは互いの隣接点

G=(V,E)

完全グラフ

  • 完全グラフ
    • 全ての頂点が互いに隣接している。
    • \(n\)頂点完全グラフの辺の数は\(\frac{n(n+1)}{2}\)

特殊な辺

  • ループ(自己辺)
    • 両端の頂点が同じ
  • 多重辺
    • 同じ辺が複数
  • 単純グラフ(simple graph)
    • ループと多重辺を含まないグラフ

次数

  • 頂点vの次数
    • ​vに繋がっている辺の個数
  • 孤立点
    • 次数0の頂点

入次数・出次数

  • 有向グラフの時のみの概念
    • 入次数
      • 自分に向かう辺の数
    • 出次数
      • 自分から出て行く辺の数

2の入次数は2

2の出次数は1

道(パス)

  • 道(path)
    • いくつかの頂点をある順序で通る通り道
    • 元のグラフの部分グラフ\(P=(V,E)\)のこと
      • \(V=\{v_0,v_1,..,v_k\}\)
      • \(E=\{(v_0,v_1),..,(v_{k-1},v_k)\}\)
    • 通る順序が分かれば良いので、頂点を通る順に並べられる。
    • 始点、終点の2点をまとめて端点と呼ぶ

道 {4,1,2,3}

閉路

  • 閉路(cycle)
    • 始点と終点が同じ道
    • つまり、ぐるっと一周できる道

道{4,5,2,1,4}

距離

  • 頂点uからvまでの距離
    • 頂点uからvまでの最小の辺の数。
    • 辺に長さ(重み)がある場合もある(そのときの距離は最小の長さの和)

連結

  • 連結
    • どの2つの頂点間にも道が存在するグラフ
    • 要は、全頂点が間接的に繋がってるグラフ

連結成分

  • 連結成分
    • 空でなく、極大な(これ以上大きくできない)連結な部分グラフ

橋

  • その辺を除くと、グラフが連結でなくなるような辺。

木

  • 木
    • 連結で閉路のないグラフ
      • 多重辺,ループ\(\in\)閉路なのでない
      • cf. アルカン
    • 任意の2頂点間に道が1つしかない
    • \(|V|-1\)本の辺を持つ。
  • 葉
    • 木の中の次数が１の点

木

葉

葉

葉

根つき木

  • 根つき木
    • 根という特別な頂点を定めた木
    • 一般に根を上に持ってきて図示する
    • uとvが隣接していて、uの方が根に近い(上にある)とき、
      • uをvの親と呼ぶ
      • vをuの子と呼ぶ
      • 家系図みたいな雰囲気
    • 家系図とか樹形図が根つき木に当たる。

根つき木

葉

葉

葉

根

さっきの木の図で2を根にした

根つき木

根つき木：補足

  • １つの頂点に対して親が2つ以上あることはあり得ない。
    • 閉路がないため。
    • １つの辺を持ち上げると、他の辺は全て下側に落ちるため。

グラフ表現

グラフ表現

  • さっきまでやってたグラフをプログラミングでどのように表現(実装)するの？？？
  • 要は頂点と辺の状態があれば良い。

グラフ表現：目次

  1. 隣接行列
  2. 隣接リスト (重要！)
  3. 辺の集合で管理
  4. 接続行列
  5. (発展)ラプラシアン行列

1. 隣接行列

サイズ\(|V|\times |V|\)の二次元配列\(A=a_{uv}\)

{\large a_{uv}=} \begin{cases} 1&\text{(u,vが隣接している)}\\ \infty&\text{(u,vが隣接していない)} \end{cases}
  • 計算量大きくなりがち
  • \(a_{uv}=w_{uv}\)とすれば簡単に辺の重みに対応できる。
  • 多重辺には対応できない。
  • \(a_{uv}= a_{vu}\)とすれば無向辺、\(a_{uv}\)≠ \(a_{vu}\)とすれば有向辺に対応可。

1. 隣接行列_図(無向辺)

const int INF = 1e7;  //とても大きい値を無限としておく。
int V,E;
cin >> V >> E;  //Vは与えられた頂点数,Eは辺の数
vector<vector<int>> a(V,vector<int>(V,INF));//V*Vを無限で初期化
for(int i=0;i<E;++i){
    //s→tへの有向辺として入力が与えられたとする。//wは重み
    int s,t;       //,w
    cin >> s >> t; //>>w
    a[s][t] = 1;   //a[s][t] = w;
    //a[t][s] = 1; (s-tの無向辺の場合)
}

1. 隣接行列_コード例

有向辺の時はa[s][t]をs→tと設定しよう。

無向辺の時は逆向きにも有向辺を張って対応しよう

2. 隣接リスト

サイズ\(|V|\)の配列\(A=a_{u}\)

a_{u}=
  • 計算量的にこれを使うことがかなり多い。
  • 辺の重みに対応するときは工夫が必要。
    • \(a_u\)に(頂点番号,重み)のペア(or構造体)を入れるなど

{uと隣接してる頂点たち}

a[1] = {2,4}

a[2] = {3,4,5}

a[3] = {2,4}

a[4] = {1,2,3,5}

a[5] = {2,4}

2. 隣接リスト_図(無向辺)

2. 隣接リスト_コード例

int V,E;
cin >> V >> E;  //Vは与えられた頂点数,Eは辺の数
vector<vector<int>> a(V);//V個の空ベクトルを含むベクトル
for(int i=0;i<E;++i){
    //s→tへの有向辺として入力が与えられたとする。
    int s,t; 
    cin >> s >> t;
    a[s].push_back(t);
    //a[t].push_back(s); (s-tの無向辺の場合)
}

このとき、a[u]にはuと隣接している頂点の配列が入っている。

3. 辺の集合で管理

サイズ\(|E|\)の集合\(A\)

A=
  • グラフの定義に割と近い
  • (u,v)と(v,u)を区別すれば有向辺でもOK
  • 入力は大抵この形式なので、隣接リストとかに変換しよう。
  • そのまま使うことはそんなになさそう…
  • 全ての辺に何かしたいときは使うかも

{辺の頂点のペア(u,v)たち}

3. 辺集合_図(無向辺)

4. 接続行列

サイズ\(|V|\times |E|\)の二次元配列\(A=a_{ve}\)

  • これもそんなに使わない…
  • 配列の各(縦の)列が一辺を表す。
    • なので各列の2つだけが1
    • (s,t)という辺ならs行目とt行目が1
  • 片方を-1とかにすれば有向辺にもできる。
{\large a_{uv}=} \begin{cases} 1&\text{(e番目の辺が頂点vを含む)}\\ 0&\text{(それ以外)} \end{cases}

4. 接続行列_図

5. (発展)ラプラシアン行列

サイズ\(|V|\times |V|\)の二次元配列\(A=a_{uv}\)

  • 隣接行列の進化版
    • 1の代わりに-1を使ったり、対角成分に次数を入れたり
  • 色んなメリットがあるらしいけど、必要になった時に改めて学べば良さそう
    • グラフが連結\(\Leftrightarrow\) rankA \(= |V|-1\)
    • (行列木定理)Aの任意の余因子は全域木の個数と等しい
{\large a_{uv}=} \begin{cases} \text{頂点u(=v)の次数}&\text{(u=v)}\\ -1&\text{(u,vが隣接している)}\\ \infty&\text{(else)} \end{cases}

5. ラプラシアン行列_図

あくまでも個人の意見です

  • 競プロでは隣接行列は一部のアルゴリズム(ワーシャルフロイド法)を除いてあまり使わないイメージ
  • 隣接リストはめっちゃ使う

グラフ表現まとめ

  • 色々やったけど、まずは隣接リストを習得しよう。
  • 多分今日やる問題は隣接リストを使う問題。

Union-Find木

Union-Find木って？

  • 互いに交わらない集合を扱う時に使う。
  • 分類して、それがどこにあるかを調べられる構造体。

Union-Findを使って

何ができるか？

要素と要素を結びつけるクエリが大量に投げられたとき、以下の動作を高速でおこなえる

  • 任意の要素同士が同じグループに属するかの判定
  • 任意の要素の属するグループの大きさを求める

逆に要素と要素を切り離すのは苦手

例題：Union Find

AtCoder Typical Contest 001 B(改題)

  • N個の品物をグループ分けすることを考える。
  • 最初は全ての品物が別々のグループにある。
  • 以下の２種類のクエリがQ回与えられる。
    • 連結：品物A,Bを含むそれぞれのグループをまとめる。
    • 判定：品物A,Bが同じグループか判定(Yes,No)
  • クエリを上から処理して、判定クエリに回答せよ。
  • 制約：\(N\leqq10^5,Q\leqq2\times10^5\)

例：連結クエリ

連結：1,3

これを……

例：連結クエリ

連結：1,3

こう

例：判定クエリ1

判定：2,6

例：判定クエリ1

判定：2,6

同じグループ！

よって"Yes"を出力

例：判定クエリ2

判定：1,4

例：判定クエリ2

判定：1,4

違うグループ！

よって"No"を出力

愚直解(配列)

配列を用意して、その配列に情報を入れる

1 2 3 4 5 6
1 2 2 3 1 2

グループ1

グループ2

グループ3

愚直解(配列)_計算量

1 2 3 4 5 6
1 2 2 3 1 2

グループ1

グループ2

グループ3

例えば連結クエリ：1,3の時にこの配列を全て見て、1→2にするという処理が必要

よって連結クエリで\(O(N)\)

全体で最悪\(O(NQ)\)間に合わない…

Union-Find木

  • この操作をもっと効率的に行えるデータ構造
    • unite(A,B): AとBを同じグループにする
    • find(A)      : Aの属するグループを求める
  • (STLはないので自分で実装しよう.(今日のところはコピペでもいいけど))

Union-Find木のしくみ

  • 各集合ごとに代表となる要素を決めておく。
    • 最初は全部バラバラなので自分自身が代表
    • 代表の要素を根として、根付き木の構造で持っておく。
  • unite(A,B) :「Aの集合の代表」の親を「Bの集合の代表」にする。(もちろん逆でもOK)
  • find(A)       : 順に親を辿っていき、根に着いたらそれを返す。
  • Union-Find木では子から親にしか行かないので、グラフは配列で作れる。

Union-Find木を配列で表現

赤い頂点が根

1 2 3 4 5 6 7 8 9 10
1 3 3 4 4 7 2 1 5 5

各頂点の親を入れた配列par

unite(A,B)

unite(A,B)

unite(A,B)

Union-Find第一形態_コード例

struct union_find_tree1{
    vector<int> par;//0-indexed
    union_find_tree1(int sz){ //コンストラクタ
        par.resize(sz); //サイズをszに変更
        for(int i=0;i<sz;++i) par[i] = i; //最初は自分が根
    }
    int find(int a){
        while(a!=par[a]){ //親が自分自身の時、自分が根である
            a = par[a];   //そうでないなら自分に親を代入して辿る
        }
        return a;         //引数aの根が計算されたのでそれを返す。
    }
    void unite(int a,int b){
        int root_a = find(a),root_b = find(b);  //aの根,bの根を調べて代入。
        par[root_a] = root_b;       //根aの親をbにする
    }
    bool same(int a,int b){  //aとbが同じ集合なら1,違うなら0
        return find(a)==find(b);
    }
};
int main(){  //雑だけど、構造体の使い方の例を載せときます
    int sz = 10;
    union_find_tree1 uf(sz);  //union_find木の変数ufをサイズszで宣言
    uf.unite(1,2);            //頂点1と2をunite
    if(uf.same(2,3)) puts("Yes"); //2と3が同じならYes
}

Union-Find第一形態再帰コード

struct union_find_tree1{
    vector<int> par;//0-indexed
    union_find_tree1(int sz){
        par.resize(sz); //サイズをszに変更
        for(int i=0;i<sz;++i) par[i] = i; //最初は自分が根
    }
    int find(int a){
        if(a==par[a]) return a;     //親が自分自身の時、自分が根である
        else return find(par[a]);   //そうでないなら自分に親を代入して辿る
    }
    void unite(int a,int b){
        int root_a = find(a),root_b = find(b);  //aの根,bの根を調べて代入。
        par[root_a] = root_b;       //根aの親をbにする
    }
    bool same(int a,int b){
        return find(a)==find(b);
    }
};

計算量考察

  • find(int a) : aから順番に上に辿る。
    • 一切分岐がない木だったら最悪\(O(N)\)
  • unite(int a,int b):付け替えは\(O(1)\)だが、内部でfindを使っているので\(O(N)\)

 

遅い！！！

というわけで高速化します。

高速化その１：rank

  • rank : 各木に紐ついた、木の高さを示す値
    • 最初は全て0, unite時に更新
  • 出来るだけfindで辿る回数を減らしたい。
    • →常に木が低くなるようにuniteする
  • 木A(rank=k)と木B(rank=m)の時(k>m)
    • AにBをくっつける。新しい木のrankはk
  • 木A(rank=k)と木B(rank=k)の時
    • どっちにしても同じ。新しい木のrankはk+1

rank

高速化その１：計算量考察

  • rank=kの木を構成するには少なくとも\(2^k\)の要素が必要
    • rank=0の木を構成するのに要素1つ必要
    • rank=k+1の木を構成するのにrank=kの木が2つ必要
    • 帰納的に考えると、\(2^k\)になる
  • よってn要素のUnion-Find木の高さは高々\(\log_{2}{n}\)

高速化その１：計算量考察

  • find : \(O(\log N)\)
    • 最大でも木の高さ分しか辿らない。
  • unite : \(O(\log N)\)
    • ​中でfindを(ry

十分速いけど、まだ高速化できる！

Union-Find 第二形態-1 コード

struct union_find2_1{//rankで高速化
    vector<int> par;//parは添字の親（または自分が根の時自身）を示す。
    vector<int> rank;//rankは木の高さ（根についてのみ実装）
    union_find2_1(int sz){
        par.resize(sz);
        rank.assign(sz,0);
        for(int i=0;i<sz;++i) par[i]=i;
    }
    int find(int a){//根を探す
        if(par[a]==a) return a;
        else return find(par[a]);
    }
    void unite(int a,int b){//小さい方の木の根に大きい方の根を上書きする
        int root_a = find(a),root_b = find(b);
        if(root_a==root_b) return; //既に同じなら終了
        if(rank[root_a]>rank[root_b]){
            par[root_b] = root_a;
        }else if(rank[root_a]<rank[root_b]){
            par[root_a] = root_b;
        }else{
            rank[root_a]++;
            par[root_b] = root_a;
        }
    }
};

高速化その２：経路圧縮

  • findする時に、ついでに全ての頂点を根に直接繋ぐ
  • 集合の代表さえ分かれば良いので、どの親がどう繋がってるかはどうでもいい。

高速化その２：経路圧縮

高速化その２：経路圧縮

高速化その２：経路圧縮

高速化その２：経路圧縮

高速化その２：経路圧縮

高速化その２：経路圧縮

高速化その２：計算量

  • find:\(O(\log N)\)
  • unite:\(O(\log N)\)
    • ​中でfind(ry

これは償却計算量(計算量の平均みたいな)

なんでこうなるのかは難しいらしい…

僕は知らないので、興味ある人は調べてみてね

Union-Find 第二形態-2

struct union_find2_2{//経路圧縮で高速化
    vector<int> par;//parは添字の親（または自分が根の時自身）を示す。
    union_find2_2(int sz){
        par.resize(sz);
        for(int i=0;i<sz;++i) par[i]=i;
    }
    int find(int a){//根を探す
        if(par[a]==a) return a;
        else return par[a] = find(par[a]); //経路圧縮！！！
    }
    void unite(int a,int b){
        int root_a = find(a),root_b = find(b);  //aの根,bの根を調べて代入。
        par[root_a] = root_b;                   //根aの親をbにする
    }
    bool same(int a,int b){
        return find(a)==find(b);
    }
};

高速化その１＋その２

  • rankの計算と経路圧縮の両方を行う。
  • 経路圧縮すると、木の高さは変わるが、その際はrankを再計算しなくても良い。
    • 要するに、経路圧縮してない時と同じでOK
    • もともと「こっちにつけると\(\log N\)になるよ」というヒントなので厳密でなくて良い

高速化その１＋その２

これも償却計算量(計算量の平均みたいな)

  • find:\(O(\alpha(N))\)
    • \(\alpha(n)\)はアッカーマン関数の逆関数
    • アッカーマン関数はすごい勢いで爆発するので実質定数と言われるほど
  • unite:\(O(\alpha(N))\)
    • ​中で(ry

Union-Find 最終形態_コード例

struct union_find{//rank,経路圧縮で高速化
    vector<int> par;//parは添字の親（または自分が根の時自身）を示す。
    vector<int> rank;//rankは木の高さ（根についてのみ実装,0-indexed）
    union_find(int sz){//コンストラクタ,sz個のノードを作成し、自分を親につける
        par.resize(sz);
        rank.assign(sz,0); //rankは最初0
        for(int i = 0;i < sz;++i) par[i]=i;
    }
    int find(int a){//根を探す
        if(par[a]==a) return a; //親が自身を指す時、根である
        else return par[a] = find(par[a]);//根に直接つける
    }
    void unite(int a,int b){//小さい方の木の根に大きい方の根を上書きする
        int root_a,root_b;
        root_a = find(a),root_b = find(b);
        if(rank[root_a]>rank[root_b]){ //rankの高い方の根に低い方の根をつける
            par[root_b] = root_a;
        }else if(rank[root_a]<rank[root_b]){
            par[root_a] = root_b;
        }else{ //rankが同じ時、適当な方につけ、つけられた方のrankを1増やす
            rank[root_a]++;
            par[root_b] = root_a;
        }
    }
    bool same(int a,int b){return find(a)==find(b);}
};

Union-Find 経路圧縮(not struct)

vector<ll> par;
ll root(ll x){
  if (par[x] == x){ //根
    return x;
  }
  else {
    return par[x] = root(par[x]); //経路圧縮
  }
}
void unite(ll x,ll y){
  x = root(x);
  y = root(y);
  if (x == y){}
  else{
    par[x] = y;     //xの親をyの親にする
  }
}
ll same(ll x,ll y){
  return root(x) == root(y);
}

int main(){
  ll n;
  cin>>n;
  par.assign(n,0);
  for(ll i=0;i<n;i++){
    par[i]=i;
  }
}

参考：アッカーマン関数

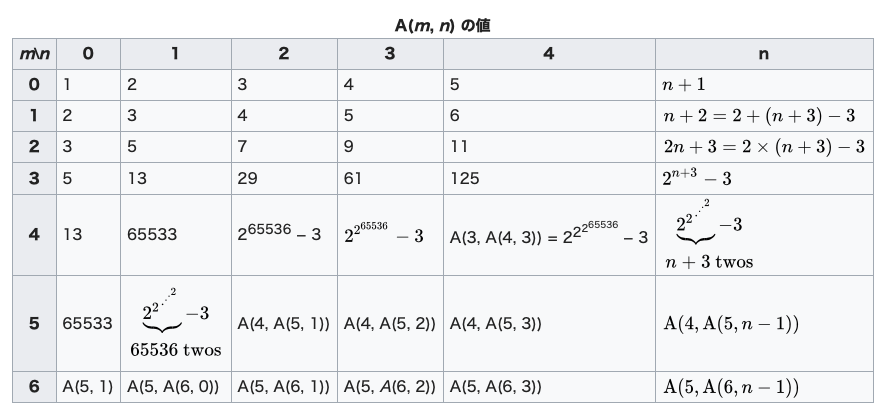
\(\alpha(n)\)はA(n,n)の逆関数

つまりは高々４

定義とかは暇な時にでも自分で見てね

https://ja.wikipedia.org/wiki/アッカーマン関数

コンテスト

  • 相変わらずVjudgeがツンツンしているのでAtCoderバチャでやるよ

コンテスト

https://kenkoooo.com/atcoder/#/contest/show/b14c57e4-1868-468d-9120-7e5e89051401

 

終わり！

参考文献

Made with Slides.com