Abel Laureate Luis Caffarelli: a glimpse of his work

Klas Modin

Luis Ángel Caffarelli

Nationality: Argentine–American

Born: 1948

 

PhD 1972 (University of Buenos Aires)

Supervisor:

Calixto Calderón

Affiliations:

University of Minnesota 1973-1983

Courant Institute, NYU 1980-1982

University of Chicago 1983-1986

IAS Princeton 1986-1996

Courant Institute, NYU 1994-1997

University of Texas at Austin 1997-today

For his seminal contributions to regularity theory for nonlinear partial differential equations including free-boundary problems and the Monge-Ampère equation.

Research fields

Free boundary problems

Fluid dynamics (Navier-Stokes)

Stefan problem

Nonlinear PDE

Monge-Ampere equation

etc.

Focus of today

Optimal mass transport (OMT)

Question (Monge 1781): Cheapest way to transport one mass distribution to another?

\mu_0
\mu_1

Mathematical formulation:

T:\Omega\to\Omega\quad\text{s.t.}\quad T_*\mu_0 = \mu_1

Additional requirement: \(T\) should minimize

\displaystyle E(T) =
\displaystyle\int_\Omega |T(\mathbf x)-\mathbf x|d \mathbf x

Example of transport map

\mu_0 = d\mathbf x
\text{Domain}\; \Omega = \mathbb T^2
\mu_1 =
T:\Omega\to\Omega, \; T_*\mu_0 = \mu_1

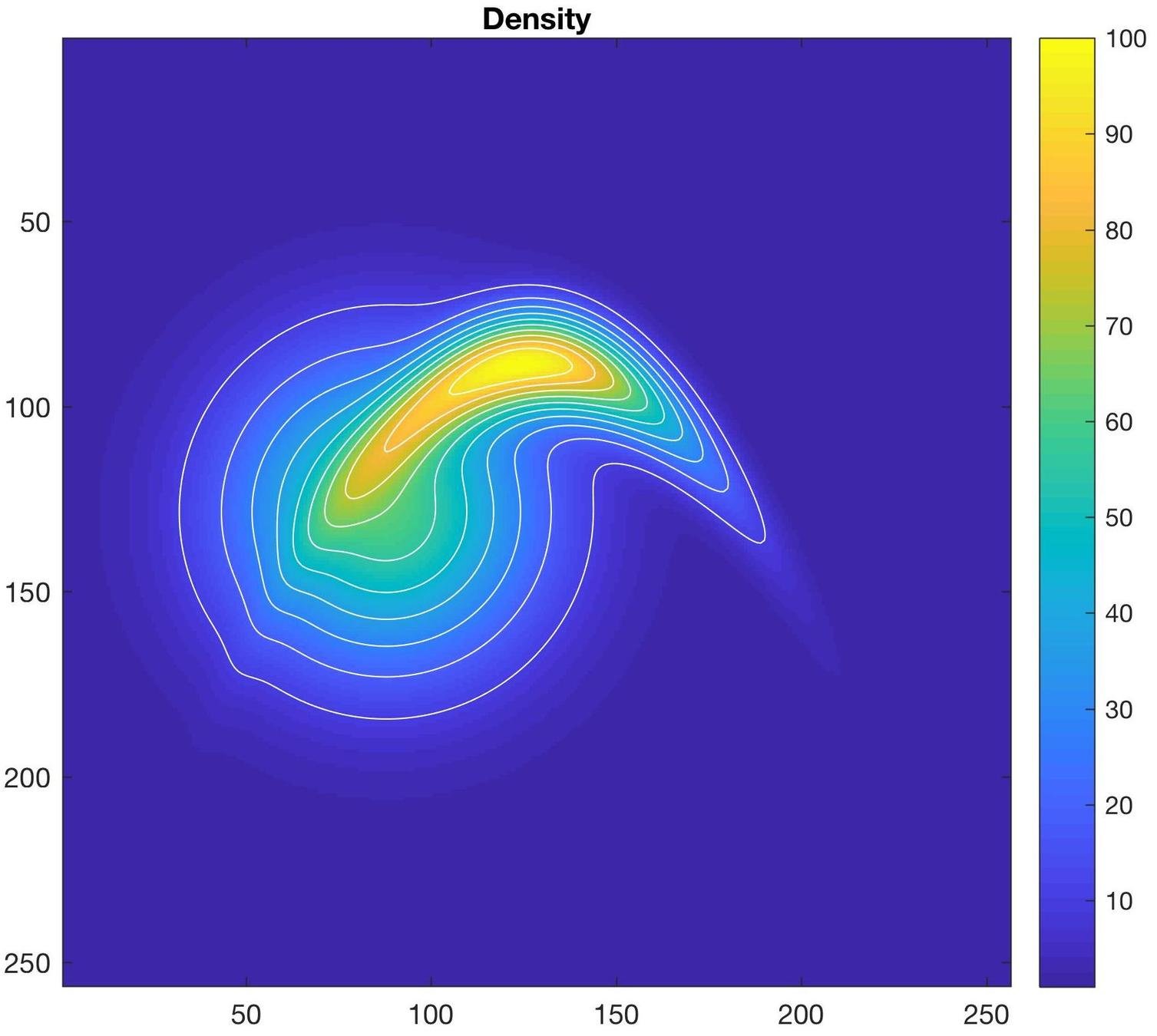
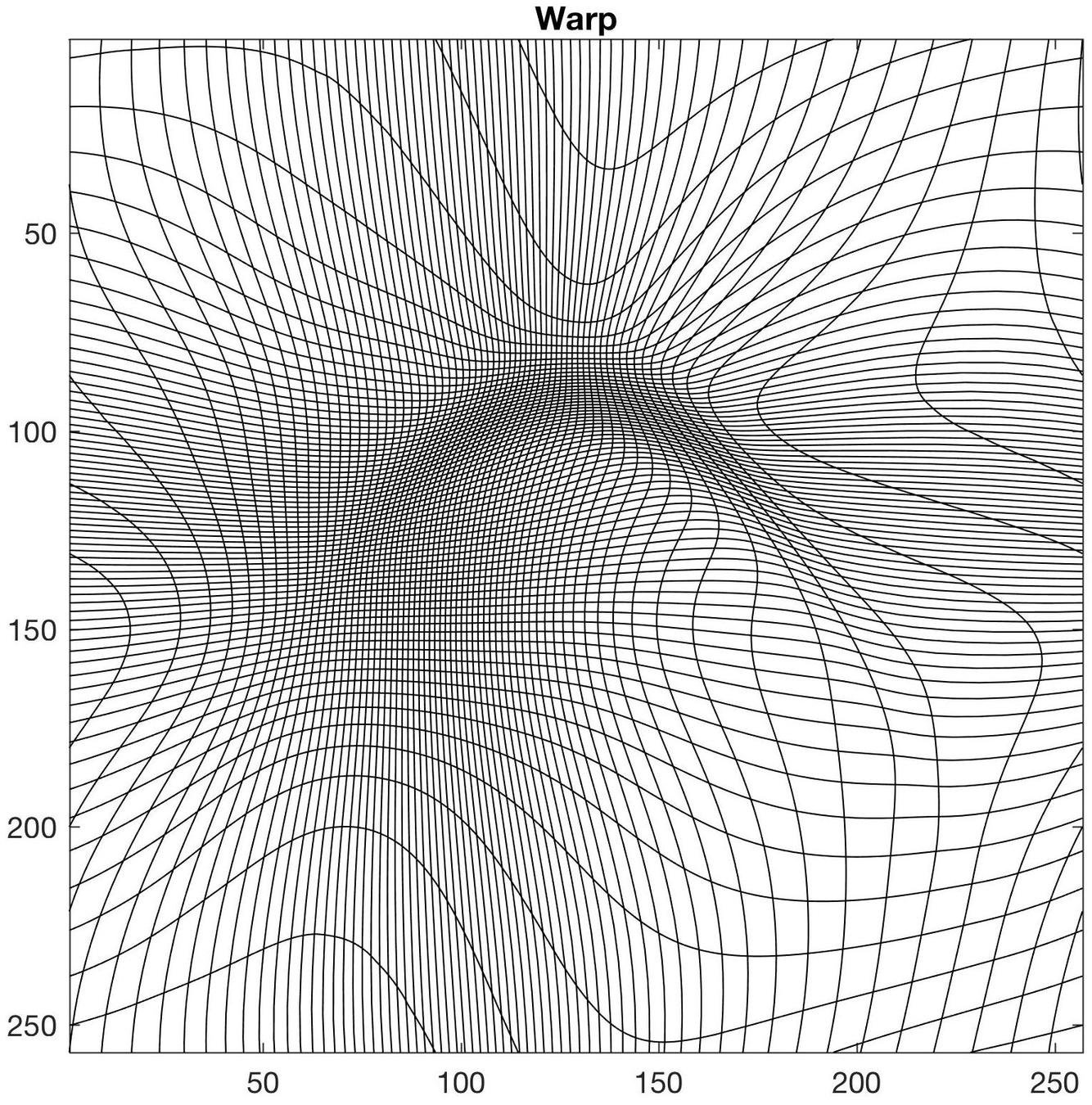
Transport map

Polar decomposition of matrices

A \in \mathbb{R}^{n\times n}
\Rightarrow \quad A = PQ
P=P^\top, \; P\geq 0
Q^\top Q = I
\Sigma_0 \in \mathrm{P}(n) = \{ \Sigma\in\mathbb{R}^{n\times n} \mid \Sigma = \Sigma^\top, \Sigma>0 \}
A \in \mathrm{GL}(n)

acts on:

A\cdot \Sigma_0 = A\Sigma_0 A^\top

via:

Bundle structure

GL(n)
P(n)\simeq GL(n)/O(n,\Sigma_0)
I
\Sigma_0
\Sigma_1
\pi(A)=A\Sigma_0 A^\top
\mathcal G_A(\dot A,\dot A) = \mathrm{tr}(\Sigma_0 \dot A^\top \dot A)
\bar{\mathcal G}_\Sigma(\dot \Sigma,\dot \Sigma) = \mathrm{tr}(\Sigma SS)
\dot\Sigma = S\Sigma + \Sigma S
K

Bundle structure

GL(n)
P(n)\simeq GL(n)/O(n,\Sigma_0)
I
\Sigma_0
\Sigma_1
\pi(A)=A\Sigma_0 A^\top
\mathcal G_A(\dot A,\dot A) = \mathrm{tr}(\Sigma_0 \dot A^\top \dot A)
\bar{\mathcal G}_\Sigma(\dot \Sigma,\dot \Sigma) = \mathrm{tr}(\Sigma SS)
\dot\Sigma = S\Sigma + \Sigma S
K = P(n)
d^2(\Sigma_0,\Sigma_1) = \lVert I - P \rVert^2_{F,\Sigma_0}

Bundle structure

GL(n)
P(n)\simeq GL(n)/O(n,\Sigma_0)
I
\Sigma_0
\Sigma_1
\pi(P)=P\Sigma_0 P = \Sigma_1
\mathcal G_A(\dot A,\dot A) = \mathrm{tr}(\Sigma_0 \dot A^\top \dot A)
\bar{\mathcal G}_\Sigma(\dot \Sigma,\dot \Sigma) = \mathrm{tr}(\Sigma SS)
\dot\Sigma = S\Sigma + \Sigma S
K = P(n)

"Square root" equation:

P

Bundle structure

GL(n)
P(n)\simeq GL(n)/O(n,\Sigma_0)
I
\Sigma_0
\Sigma_1
A = PQ
\mathcal G_A(\dot A,\dot A) = \mathrm{tr}(\Sigma_0 \dot A^\top \dot A)
\bar{\mathcal G}_\Sigma(\dot \Sigma,\dot \Sigma) = \mathrm{tr}(\Sigma SS)
\dot\Sigma = S\Sigma + \Sigma S
K = P(n)

Factorization theorem:

A
P

Bundle structure

GL(n)
P(n)\simeq GL(n)/O(n,\Sigma_0)
I
\Sigma_0
\Sigma_1
\dot B = \Omega B, \; B(0) = A
\mathcal G_A(\dot A,\dot A) = \mathrm{tr}(\Sigma_0 \dot A^\top \dot A)
\bar{\mathcal G}_\Sigma(\dot \Sigma,\dot \Sigma) = \mathrm{tr}(\Sigma SS)
\dot\Sigma = S\Sigma + \Sigma S
K = P(n)

Vertical gradient flow:

A
\Sigma_1 \Omega + \Omega\Sigma_1 = 2\Sigma_1 (B^{-1}-B^{-\top})

Bundle structure

GL(n)
P(n)
I
\Sigma_0
\Sigma_1
\dot B = \Omega B, \; B(0) = A
\mathcal G_A(\dot A,\dot A) = \mathrm{tr}(\Sigma_0 \dot A^\top \dot A)
\bar{\mathcal G}_\Sigma(\dot \Sigma,\dot \Sigma) = \mathrm{tr}(\Sigma SS)
\dot\Sigma = S\Sigma + \Sigma S
K = P(n)

Vertical gradient flow:

A
\Sigma_1 \Omega + \Omega\Sigma_1 = 2\Sigma_1 (B^{-1}-B^{-\top})

Bundle structure

GL(n)
P(n)
I
\Sigma_0
\Sigma_1
\dot \Sigma = 2I - \Sigma_1^{-1}\Sigma - \Sigma\Sigma_1^{-1}
\mathcal G_A(\dot A,\dot A) = \mathrm{tr}(\Sigma_0 \dot A^\top \dot A)
\bar{\mathcal G}_\Sigma(\dot \Sigma,\dot \Sigma) = \mathrm{tr}(\Sigma SS)
\dot\Sigma = S\Sigma + \Sigma S
K = P(n)

Horizontal gradient flow:

\Sigma(t)
\displaystyle H_{\Sigma_1}(\Sigma) = -\frac{1}{2}\mathrm{tr}(\Sigma_1^{-1}\Sigma) + \frac{1}{2}\log\det(\Sigma_1^{-1}\Sigma)

Relative entropy:

Bundle structure

GL(n)
P(n)
I
\Sigma_0
\Sigma_1
\dot P = P^{-1}\Sigma_0^{-1} - \Sigma_1^{-1}P + V
\mathcal G_A(\dot A,\dot A) = \mathrm{tr}(\Sigma_0 \dot A^\top \dot A)
\bar{\mathcal G}_\Sigma(\dot \Sigma,\dot \Sigma) = \mathrm{tr}(\Sigma SS)
\dot\Sigma = S\Sigma + \Sigma S
K = P(n)

Horizontal gradient flow:

P(t)
\displaystyle F(P) = H_{\Sigma_1}(P\Sigma_0 P)

Lifted gradient flow on \(K\) for

Bundle structure

GL(n)
P(n)
I
\Sigma_0
\Sigma_1
\dot P = P^{-1}\Sigma_0^{-1} - \Sigma_1^{-1}P + V
\mathcal G_A(\dot A,\dot A) = \mathrm{tr}(\Sigma_0 \dot A^\top \dot A)
\bar{\mathcal G}_\Sigma(\dot \Sigma,\dot \Sigma) = \mathrm{tr}(\Sigma SS)
\dot\Sigma = S\Sigma + \Sigma S
K = P(n)

Horizontal gradient flow:

P(t)

Hessian of \(F(P)\) strictly positive on \(K\) \(\Rightarrow\) unique limit!

Nice, but...

...what about Monge-Ampere and Caffarelli?!

?

Linear optimal mass transport

\(\mathrm{P}(n) \iff \)  multivariate Gaussians with zero mean

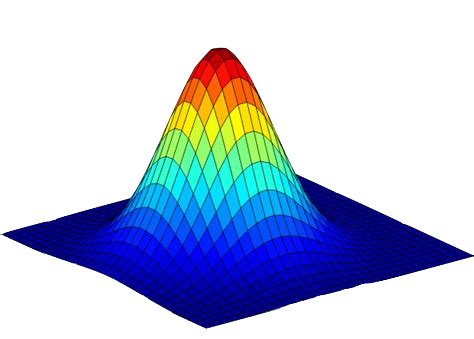
\displaystyle \rho_\Sigma(x) = \frac{1}{\sqrt{(2\pi)^n\mathrm{det}(\Sigma)}}\mathrm{exp}(-\frac{1}{2}x^\top \Sigma^{-1}x)
\Sigma \in P(n)

\(\Rightarrow\) transport map \(T:\mathbb{R}^n \to \mathbb{R}^n\) linear, \(T(x) = A x\)

T_*\rho_\Sigma = \rho_{A\Sigma A^{\top}}

\(\Rightarrow\)

\displaystyle d^2(A\Sigma_0A^\top, \Sigma_1) = \int_{\mathbb{R}^n}|T_*\rho_{\Sigma_0} - \rho_{\Sigma_1}|^2dx

\(L^2\) instead of \(L^1\) cost

Fundamental result for \(L^2\) OMT

Theorem (Brenier 1987):

\(\mu_0,\mu_1\) prob measures on \(\Omega\subset\mathbb R^n\) (open, bounded) with \(\mu_i=\rho_id \mathbf x\)
Then \((*)\) has unique solution \[ T = \nabla \psi\]

where \(\psi:\Omega \to \mathbb R\) is convex

\(\psi\) solves the weak Monge-Ampere equation \[\int_\Omega \eta \rho_1 dx = \int_\Omega (\eta\circ\nabla\psi) \rho_0 dx,\qquad \forall \eta \in C(\Omega) \]

\displaystyle \min_{T_*\mu_0=\mu_1} \int_{\Omega} |T(\mathbf x)-\mathbf x|^2 d\mu_0\qquad (*)

Note: \(\psi\in C^2(\Omega) \Rightarrow \rho_1\circ\nabla \psi\det(\nabla^2 \psi) = \rho_0 \)    (strong MA)

Fundamental result for \(L^2\) OMT

Theorem (Brenier 1991):

\(T \in L^2(\Omega,\mathbb{R}^n)\) such that \(T_*\mu_0 = \mu_1\)

Exist unique \(S:\Omega\to\Omega\) with \(S_*\mu_0 = \mu_0\) and convex \(\psi\) such that \[T = (\nabla \psi) \circ S  \]

\displaystyle \min_{T_*\mu_0=\mu_1} \int_{\Omega} |T(\mathbf x)-\mathbf x|^2 d\mu_0\qquad (*)

Note: \(\psi\in C^2(\Omega) \Rightarrow \rho_1\circ\nabla \psi\det(\nabla^2 \psi) = \rho_0 \)    (strong MA)

\mathrm{Id}
\mu_0
\mu_1
\pi(T)=T_*\mu_0
\mathrm{Hor}

\(T\)

\(\nabla\psi\)

\(S\)

Fundamental result for \(L^2\) OMT

Theorem (Brenier 1991):

\(T \in L^2(\Omega,\mathbb{R}^n)\) such that \(T_*\mu_0 = \mu_1\)

Exist unique \(S:\Omega\to\Omega\) with \(S_*\mu_0 = \mu_0\) and convex \(\psi\) such that \[T = (\nabla \psi) \circ S  \]

\displaystyle \min_{T_*\mu_0=\mu_1} \int_{\Omega} |T(\mathbf x)-\mathbf x|^2 d\mu_0\qquad (*)

Note: \(\psi\in C^2(\Omega) \Rightarrow \rho_1\circ\nabla \psi\det(\nabla^2 \psi) = \rho_0 \)    (strong MA)

Subdifferential: \(\partial \psi(x) = \{u \in\mathbb{R}^n\mid \forall y, \; \psi(y) \geq \psi(x) + u\cdot (y-x) \} \)

\(x\)

\(\psi(x)\)

\(\psi(x) + u\cdot(y-x)\)

\(\psi(y)\)

\(y\)

Regularity obstructions

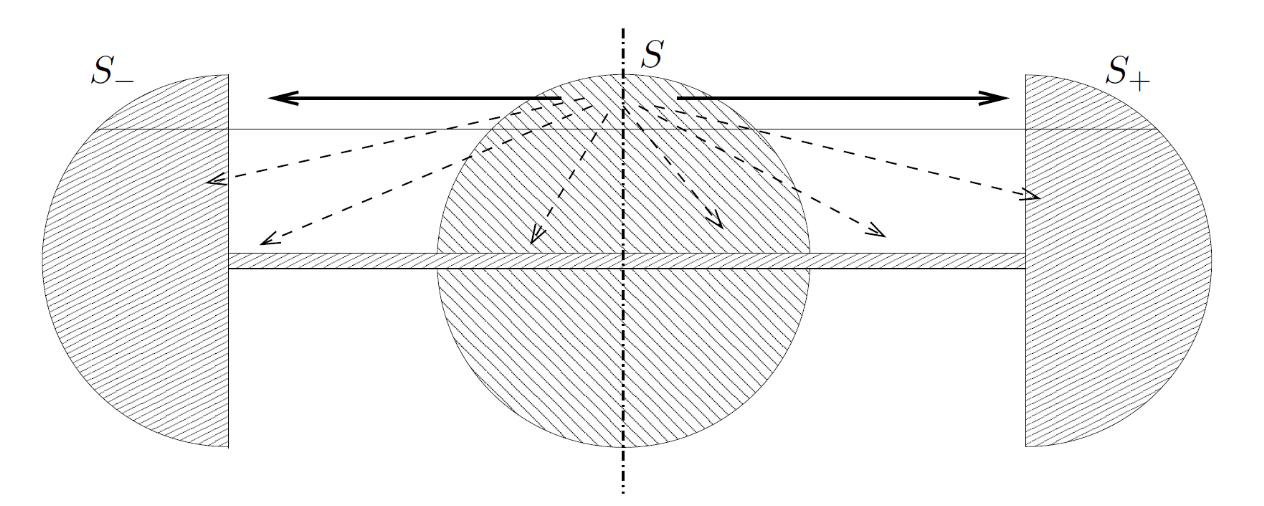
Non-convex domain

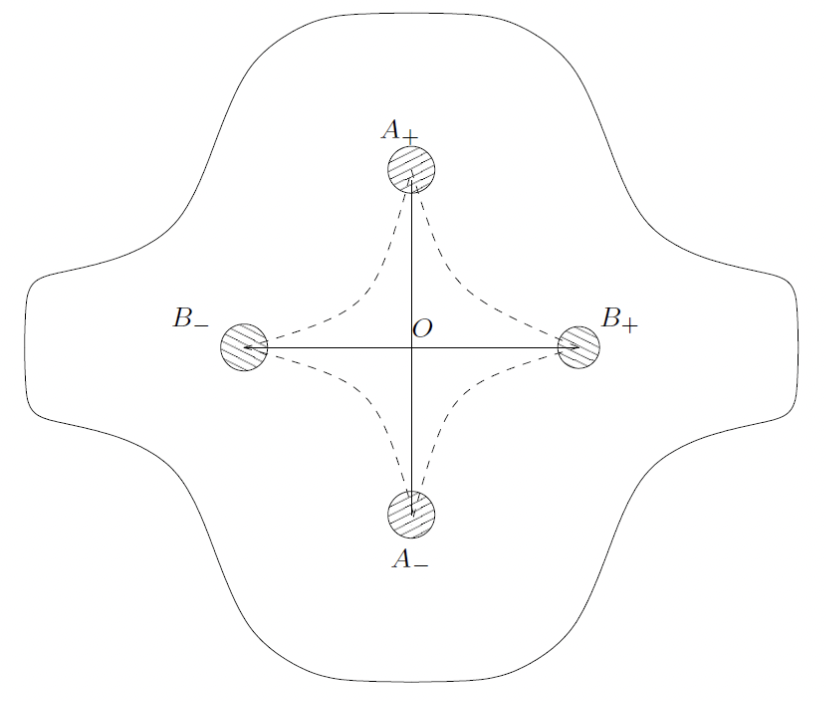
Negative curvature domain

[cf. Villani 2009]

"There is no hope for general regularity results
outside the world of nonnegative sectional curvature"

[Villani 2009]

Caffarelli's regularity theory

Theorem (Caffarelli 1992):

\(\mu_0,\mu_1\) prob measures on \(\Omega\subset\mathbb R^n\) (convex) with \(\mu_i=\rho_id \mathbf x\)

\(\rho_i \in C^{k,\alpha}(\Omega), \quad 0<a\leq \rho_i(x) \leq b < \infty \)
Then \((*)\) has unique solution \[ T = \nabla \psi\]

where \(\psi\in C^{k+2,\alpha}(\Omega)\) is convex

\(\psi\) solves the strong Monge-Ampere equation \[\rho_1\circ\nabla \psi\det(\nabla^2 \psi) = \rho_0 \]

\displaystyle \min_{T_*\mu_0=\mu_1} \int_{\Omega} |T(\mathbf x)-\mathbf x|^2 d\mu_0\qquad (*)

Riemannian structure of OMT

\mathrm{Diff}(\Omega)
\mathrm{P}^{\infty}(\Omega)
\mathrm{Id}
\mu_0
\mu_1
\pi(T)=T_*\mu_0

Riemannian metric

\displaystyle\mathcal{G}_T(\dot T,\dot T) = \int_{\Omega}\left\vert \dot T \right\vert^2 \mu_0

Induces metric

\overline{\mathcal{G}}_\mu(\dot\mu,\dot\mu) \Rightarrow d_W^2(\mu_0,\mu_1)
\mathrm{Hor}

[Benamou & Brenier (2000), Otto (2001)]

Invariance: \( S\in\mathrm{Diff}_{\mu_0}(\Omega)\)

\displaystyle\mathcal{G}_T(\dot T,\dot T) = \mathcal{G}_{T\circ S}(\dot T\circ S, \dot T\circ S)

Exactly \(L^2\)-Wasserstein distance

\mathrm{Diff}_{\mu_0}(\Omega)

OMT \(\leftrightarrow\) hydrodynamics

\displaystyle \pi: F\mapsto F_*d\mathbf{x}

[Arnold 1966, Hamilton 1982, Caffarelli 1992, Benamou and Brenier 2000, Otto 2001]

\displaystyle \mathrm{Diff}(\Omega)
\displaystyle \mathrm{id}
\displaystyle \mathrm{SDiff}(\Omega)
\displaystyle F
\displaystyle \nabla P
\displaystyle S
\displaystyle \mathcal{P}^\infty(\Omega) \simeq \mathrm{Diff}(\Omega)/\mathrm{SDiff}(\Omega)
\displaystyle d\mathbf{x}
\displaystyle \rho\, d\mathbf{x}

Brenier's polar

factorization: \(F = \nabla P\circ S\)

Remember:

\(T = \nabla P\) solves OMT problem with \(\mu_0 = d\mathbf x\) and \(\mu_1 = \rho\,d\mathbf x\)

hydrodynamics

OMT

Summary

Slides available at: slides.com/kmodin

(from an applied perspective)

Caffarelli's work enables "safe ground" for geometers to work with smooth optimal transport