Glimpse into the work of Alessio Figalli

Klas Modin

Seminar series about Fields Medalists 2018

Alessio Figalli

Nationality: Italian

Born: 1984

Master's degree 2006 (SNS Pisa)

PhD 2007 (SNS Pisa and ENS Lyon)

Supervisors:

Luigi Ambrosio (SNS Pisa)

Cedric Villani (ENS Lyon)

Affiliations:

CNRS 2007

École polytechnique 2008-2009

University of Texas in Austin 2009-2016

ETH Zürich 2016-today

Awarded the Fields Medal for his contributions to the theory of optimal transport and its applications in partial differential equations, metric geometry, and probability

Research fields

Optimal mass transport (OMT)

Fluid dynamics (Euler equations, etc)

Weak KAM theory

Geometric measure theory

Stochastic analysis

Random matrices

etc.

Very productive 120+ papers, 2 books, 25 lecture notes, ...

Focus of today

Optimal mass transport (OMT)

Question (Monge 1781): Cheapest way to transport one mass distribution to another?

\mu_0

\mu_1

Mathematical formulation:

T:\Omega\to\Omega\quad\text{s.t.}\quad T_*\mu_0 = \mu_1

Additional requirement: \(T\) should minimize

\displaystyle E(T) =

\displaystyle\int_\Omega c(T(\mathbf x),\mathbf x)d \mathbf x

\displaystyle\int_\Omega |T(\mathbf x)-\mathbf x|^2d \mathbf x

Example of transport map

\mu_0 = d\mathbf x

\text{Domain}\; \Omega = \mathbb T^2

\mu_1 =

T:\Omega\to\Omega, \; T_*\mu_0 = \mu_1

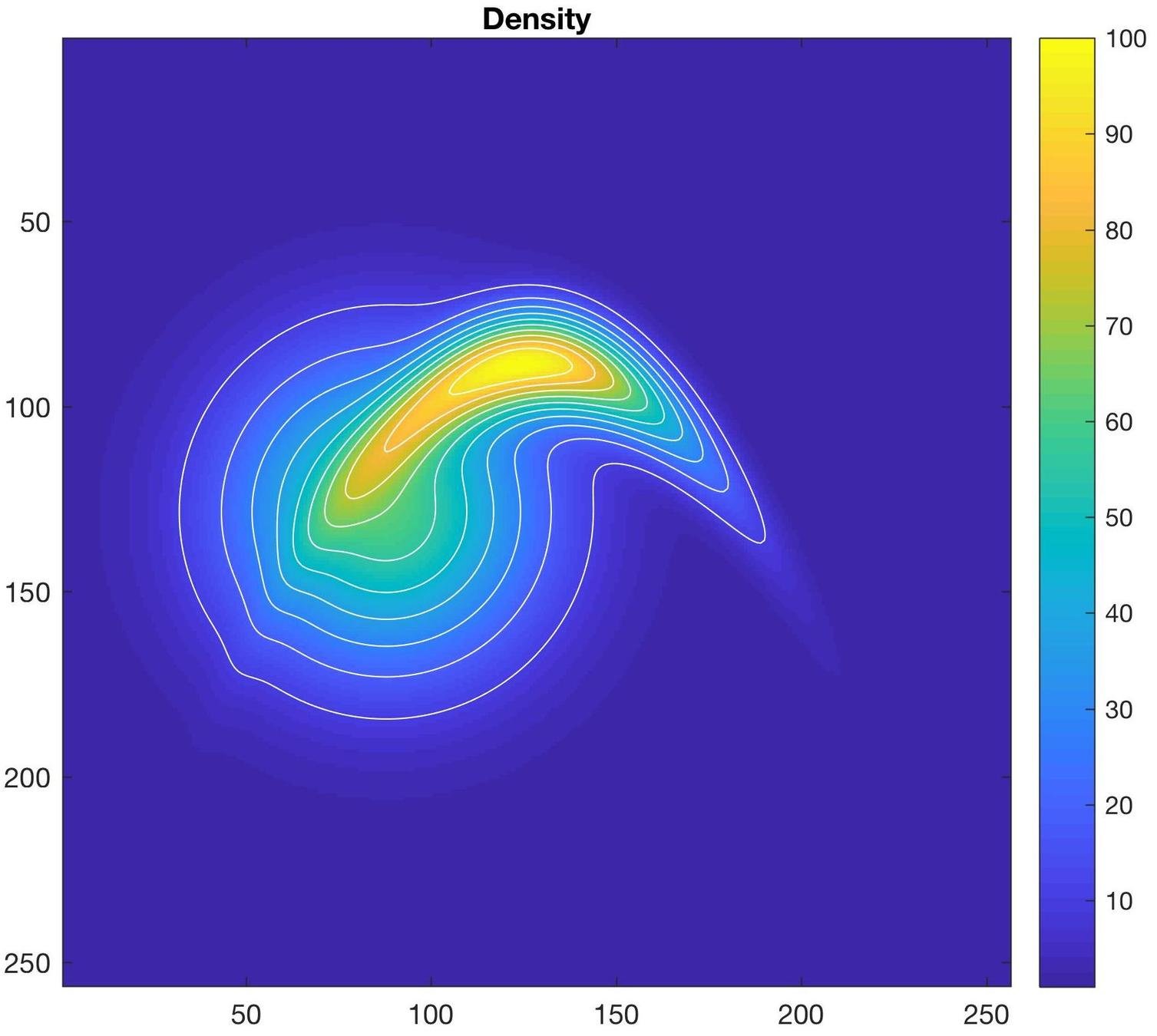
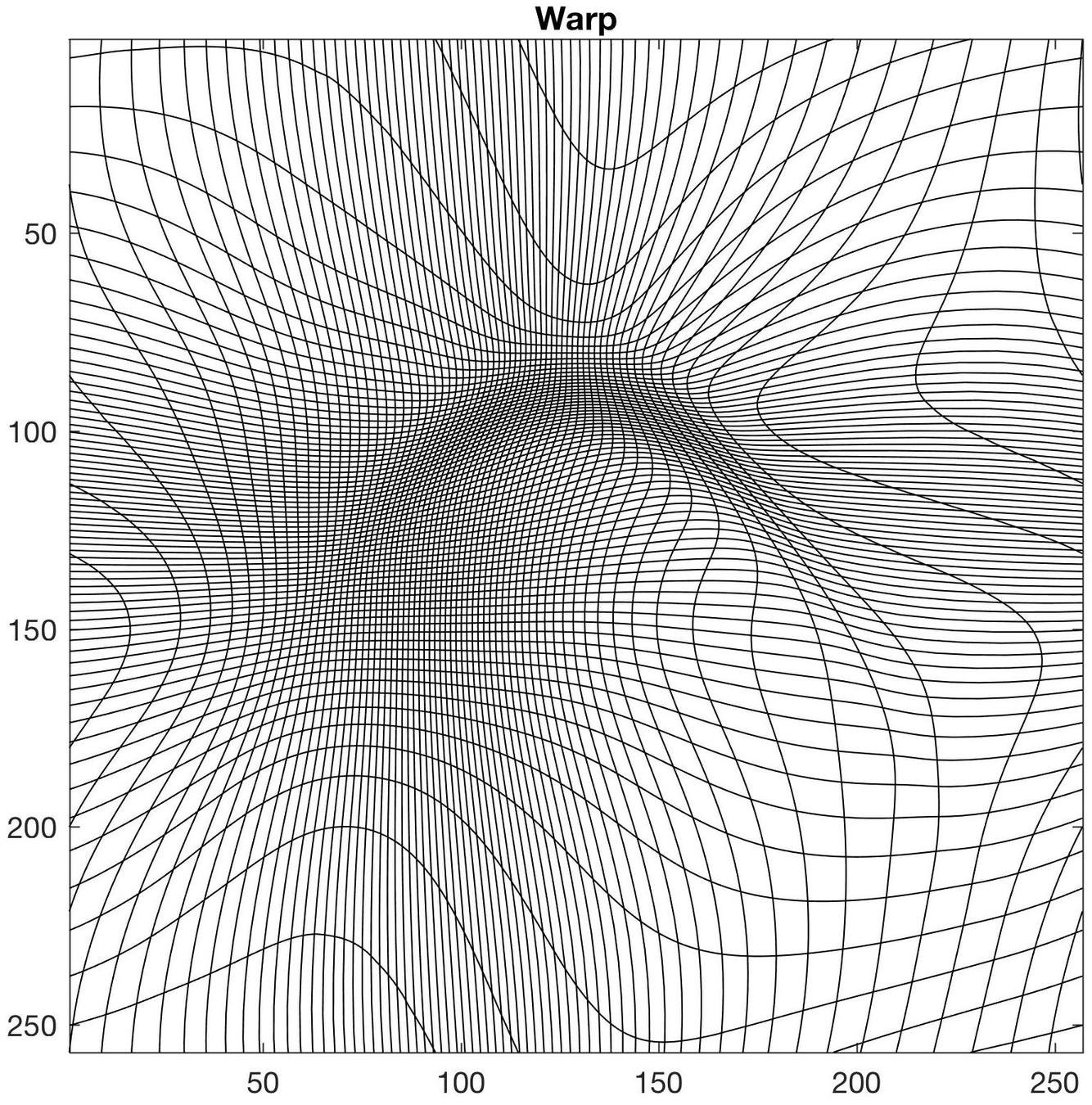
Transport map

Fundamental result for \(L^2\) OMT

Theorem (Brenier 1991):

\(\mu_0,\mu_1\) prob measures on \(\mathbb R^n\) with finite second moment, \(\mu_0=\rho_0d \mathbf x\)
Then \((*)\) has unique solution \[ T = \nabla P\]

where \(P:\mathbb R^n \to \mathbb R\) is convex

If \(\mu_1 = \rho_1 d\mathbf x\) then (formally) \(P\) solves the Monge-Ampere equation \[ \det(D^2P) = \frac{\rho_0}{\rho_1\circ\nabla P} \iff \text{MA}(P) = \frac{\rho_0}{\rho_1\circ\nabla P} \]

\displaystyle \min_{T_*\mu_0=\mu_1} \int_{\mathbb R^n} |T(\mathbf x)-\mathbf x|^2 d\mu_0\qquad (*)

Sobolev result for \(L^2\) OMT

Theorem (De Philippis and Figalli 2013):

If \(\Omega\subset \mathbb R^n\) is convex and bounded, \(P:\Omega\to\mathbb R\) is convex, and \[ 0 < \lambda \leq \det(D^2 P) \leq \Lambda < \infty \]

then \(P \in W^{2,1}_{\text{loc}}(\Omega)\)

Corollary

The solution \( T = \nabla P\) to \((*)\) belong to \(W^{1,1}_{\text{loc}}(\Omega)\)

\displaystyle \min_{T_*d\mathbf x=\rho d\mathbf x} \int_{\Omega} |T(\mathbf x)-\mathbf x|^2 d\mathbf x\qquad (*)

Incompressible hydrodynamics

\displaystyle\frac{\partial \mathbf v}{\partial t} + \mathbf v\cdot \nabla \mathbf v = -\nabla p\qquad (*)

Domain \(\Omega\subset \mathbb R^3\), velocity field \(\mathbf v = \mathbf v(t,\mathbf x)\)

Discovery by Arnold 1966:

Solutions to \((*)\) correspond to geodesics on the infinite-dimensional manifold \(\mathrm{SDiff}(\Omega)\) with Riemannian \(L^2\)-metric \[\langle V,V\rangle_{S} = \int_\Omega |V|^2 d \mathbf x \] where \[\mathbf v = V\circ S^{-1} \]

\displaystyle \nabla \cdot\mathbf v = 0

pressure

OMT \(\leftrightarrow\) hydrodynamics

\displaystyle \pi: F\mapsto F_*d\mathbf{x}

(Benamou and Brenier 2000, Otto 2001)

\displaystyle \mathrm{Diff}(\Omega)

\displaystyle \mathrm{id}

\displaystyle \mathrm{SDiff}(\Omega)

\displaystyle F

\displaystyle \nabla P

\displaystyle S

\displaystyle \mathcal{P}^\infty(\Omega) \simeq \mathrm{Diff}(\Omega)/\mathrm{SDiff}(\Omega)

\displaystyle d\mathbf{x}

\displaystyle \rho\, d\mathbf{x}

Brenier's polar

factorization: \(F = \nabla P\circ S\)

Remember:

\(T = \nabla P\) solves OMT problem with \(\mu_0 = d\mathbf x\) and \(\mu_1 = \rho\,d\mathbf x\)

hydrodynamics

OMT

Atmospheric hydrodynamics

\displaystyle\frac{\partial \mathbf v}{\partial t} + \mathbf v\cdot \nabla \mathbf v = -\nabla p + \begin{pmatrix}v_2 \\ -v_1 \\ 0\end{pmatrix} + \mathbf{g}

\displaystyle \nabla \cdot\mathbf v = 0

Semi-geostrophic wind:

Coriolis force

\displaystyle \mathbf v^g = \begin{pmatrix}\partial_2 p \\ -\partial_1 p \end{pmatrix}

Aim: equation for \(\mathbf v^g\)

Semigeostrophic equation (SGE)

\displaystyle\frac{\partial \nabla p}{\partial t} + (\mathbf v\cdot \nabla) \nabla p = -J\nabla p - \mathbf v

\displaystyle \nabla \cdot\mathbf v = 0

where

Now 2D: \(\mathbf v = (v_1,v_2)\) and replace l.h.s. by semi-geostrophic wind

J = \begin{pmatrix}0 & 1 \\ -1 & 0 \end{pmatrix}

Notice: no time-derivative on \(\mathbf v\)

As written, SGE is hard to analyze!

Rewrite in simpler form?

(Hoskins and Bretherton 1972)

Brief derivation of dual SGE

\displaystyle \mathbf u = \frac{\partial T}{\partial t}\circ T^{-1} = \frac{\partial \nabla P}{\partial t}\circ \nabla P^*

\displaystyle P(t,\mathbf x) = p(t,\mathbf x) + \frac{|\mathbf x|^2}{2}

Change of variables:

(assume \(P\) convex)

\displaystyle \rho\,d\mathbf x = (\nabla P)_*d\mathbf x

Key: Think of \(T=\nabla P\) as transport map

Apply Arnold's approach:

right translation of \(\partial_t T\) gives vector field

\displaystyle \mathbf u = J(\nabla P^*-\mathbf x)

By construction

\displaystyle \frac{\partial \rho}{\partial t} + \nabla\cdot(\rho \mathbf u) = 0

Dual SGE

\displaystyle \rho = \det(D^2 P^*) \iff \rho = \text{MA}(P^*)

\displaystyle \frac{\partial \rho}{\partial t} + \nabla\cdot(\rho \mathbf u) = 0

\displaystyle \rho\,d\mathbf x = (\nabla P)_*d\mathbf x = (\nabla P^*)^*d\mathbf x

\displaystyle \mathbf u = J(\nabla P^*-\mathbf x)

Close relation to vorticity equation

\displaystyle \frac{\partial \omega}{\partial t} + \nabla\cdot(\omega \mathbf u) = 0

\displaystyle \mathbf u = J\nabla \psi

\displaystyle \omega = \Delta\psi

\displaystyle \rho \sim \omega + 1

\displaystyle P^* \sim \psi+\frac{|\mathbf x|^2}{2}

\displaystyle \text{MA}(P^*) = \det(I + D^2\psi)

\displaystyle \approx 1 + \Delta\psi

Problem with existence for SGE

Theorem (Benamou and Brenier 1998):

Dual SGE admits global weak solution

\displaystyle\frac{\partial \nabla p}{\partial t} + (\mathbf v\cdot \nabla) \nabla p = -J\nabla p - \mathbf v

\displaystyle \nabla \cdot\mathbf v = 0

Recall: SGE

Does weak dual SGE solution give solution to SGE?

How is \(p,\mathbf v\) reconstructed from \(\rho,P^*\) ?

\displaystyle p = P -\frac{|\mathbf x|^2}{2}

\displaystyle \mathbf v = - D^2P^*\circ\nabla P\Big(\partial_t\nabla P+ J(\nabla P - \mathbf x) \Big)

Easy!

Problem: no meaning a priori

Existence theorem for SGE

Theorem (Ambrosio, Colombo, De Philippis, Figalli 2012):

\((\rho,P^*)\) weak solution to dual SGE on \(\mathbb T^2\) with initial data fulfilling

\(P_0^*\) convex
\( 0 < \lambda \leq \rho_0 \leq \Lambda < \infty \)

Then \[\mathbf v = - D^2P^*\circ\nabla P\Big(\partial_t\nabla P+ J(\nabla P - \mathbf x) \Big)\] is well-defined weakly and \((\mathbf v,p=P -\frac{|\mathbf x|^2}{2}) \) is weak solution to SGE

Proof uses:

Condition \((*)\) retained through time (\(\rho\) is transported)
\(\lambda \leq \det(D^2P) \leq \Lambda \Rightarrow P\in W^{2,1}\) by De Philippis and Figalli

\((*)\)

THANKS!

References

G. De Philippis, A. Figalli
\(W^{2,1}\) regularity for solutions of the Monge-Ampere equation
Invent. Math. (2013)
L. Ambrosio, M. Colombo, G. De Philippis, A. Figalli
Existence of Eulerian solutions to the semigeostrophic equations in physical space: the 2-dimensional periodic case
Comm. Partial Differential Equations (2012)

Slides available at: slides.com/kmodin