Collaborator: Olivier Verdier

Reference:
What makes nonholonomic integrators work? Num. Math. (2020) 145:405-435

Constrained Lagrangian systems

Lagrange-d'Alembert

\displaystyle\delta \int_a^b L(\mathbf{q}(t),\dot{\mathbf{q}}(t))dt = 0

\displaystyle\delta \int_a^b L(\mathbf{q}(t),\dot{\mathbf{q}}(t))dt = 0

for virtual displacements $\delta\mathbf{q}$

A(\mathbf{q}(t))\delta\mathbf{q}(t) = 0

A(\mathbf{q}(t))\delta\mathbf{q}(t) = 0

Constraint defined by distribution $A(\mathbf{q})\dot{\mathbf{q}}=0$

Constrained Lagrangian systems

Lagrange-d'Alembert

\displaystyle\delta \int_a^b L(\mathbf{q}(t),\dot{\mathbf{q}}(t))dt = 0

\displaystyle\delta \int_a^b L(\mathbf{q}(t),\dot{\mathbf{q}}(t))dt = 0

for virtual displacements $\delta\mathbf{q}$

A(\mathbf{q}(t))\delta\mathbf{q}(t) = 0

A(\mathbf{q}(t))\delta\mathbf{q}(t) = 0

Constraint defined by distribution $A(\mathbf{q})\dot{\mathbf{q}}=0$

Holonomic systems

\displaystyle A(\mathbf q)\dot{\mathbf q} = \frac{d}{dt}\mathbf F(\mathbf q)

\displaystyle A(\mathbf q)\dot{\mathbf q} = \frac{d}{dt}\mathbf F(\mathbf q)

\mathcal C = \{ \mathbf{q}\in \mathcal Q \mid \mathbf F(\mathbf q) = 0 \}

\mathcal C = \{ \mathbf{q}\in \mathcal Q \mid \mathbf F(\mathbf q) = 0 \}

Distribution is integrable
$\Rightarrow$ Lagrangian dynamics on $T\mathcal C$

Nonholonomic systems

\displaystyle A(\mathbf q)\dot{\mathbf q} \neq \frac{d}{dt}\mathbf F(\mathbf q)

\displaystyle A(\mathbf q)\dot{\mathbf q} \neq \frac{d}{dt}\mathbf F(\mathbf q)

\mathcal M = \text{state space}

\mathcal M = \text{state space}

Distribution nonintegrable

\mathbf q

\mathbf q

\dot{\mathbf q}

\dot{\mathbf q}

\mathbf q\cdot\dot{\mathbf q} = 0

\mathbf q\cdot\dot{\mathbf q} = 0

Holonomic systems

\displaystyle A(\mathbf q)\dot{\mathbf q} = \frac{d}{dt}\mathbf F(\mathbf q)

\displaystyle A(\mathbf q)\dot{\mathbf q} = \frac{d}{dt}\mathbf F(\mathbf q)

\mathcal C = \{ \mathbf{q}\in \mathcal Q \mid \mathbf F(\mathbf q) = 0 \}

\mathcal C = \{ \mathbf{q}\in \mathcal Q \mid \mathbf F(\mathbf q) = 0 \}

Distribution is integrable
$\Rightarrow$ Lagrangian dynamics on $T\mathcal C$

Nonholonomic systems

\displaystyle A(\mathbf q)\dot{\mathbf q} \neq \frac{d}{dt}\mathbf F(\mathbf q)

\displaystyle A(\mathbf q)\dot{\mathbf q} \neq \frac{d}{dt}\mathbf F(\mathbf q)

\mathcal M = \text{state space}

\mathcal M = \text{state space}

Distribution nonintegrable

\mathbf q

\mathbf q

\dot{\mathbf q}

\dot{\mathbf q}

\mathbf q\cdot\dot{\mathbf q} = 0

\mathbf q\cdot\dot{\mathbf q} = 0

Nonholonomic examples

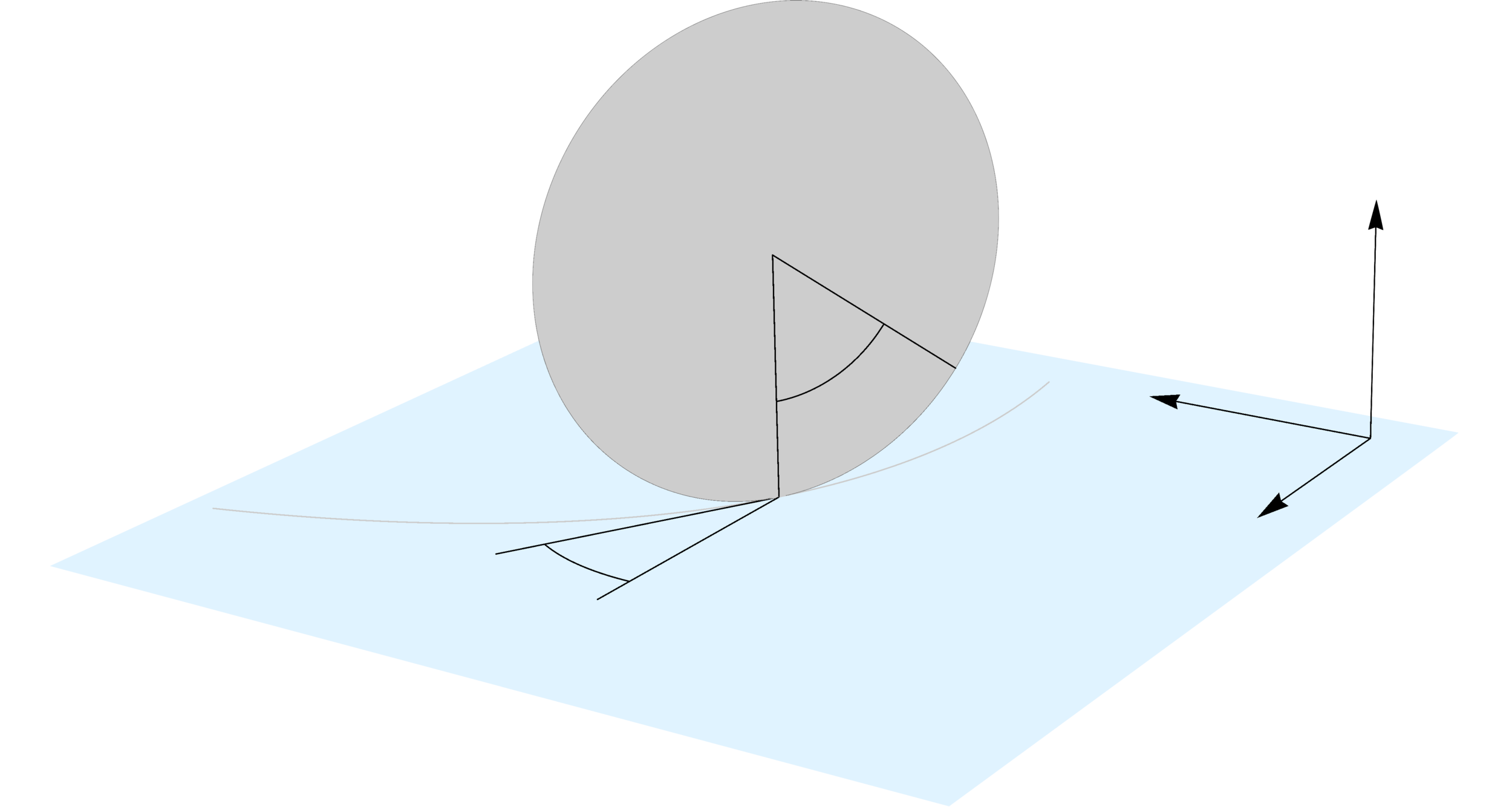
Rolling disk

Nonholonomic examples

Knife edge

Nonholonomic examples

Continuously variable transmission (CVT)

What makes holonomic integrators work?

Definition: Numerical integrator

Map $\Phi_h: (\mathbf{q}_{k},\dot{\mathbf{q}}_{k})\mapsto (\mathbf{q}_{k+1},\dot{\mathbf{q}}_{k+1})$ that preserves constraints and approximates exact flow $\varphi^h$

Exact flow $\varphi^h$ $\Rightarrow$ Hamiltonian system on $T^*\mathcal C$

Geometric numerical integration and backward error analysis:

Integrator is exact flow of modified system on $T^*\mathcal C$
Modified system Hamiltonian?
$\Rightarrow$ modified Hamiltonian preserved
Original system Arnold-Liouville integrable?
$\Rightarrow$ KAM stability of tori

What about nonholonomic integrators?

Exact flow $\varphi^h$ $\Rightarrow$ energy system on $\mathcal M$

Is that all?
Not clear what "structure preserving" means

Idea: discrete analog of Lagrange d'Alembert (DLA)

[Cortés Monforte and Martínez 2001]

[McLachlan and Perlmutter 2006]

Energy

Time

Why so good?

Notion: additional structure behind long-time behaviour

Strategy

Identify structure of standard nonholonomic test problems

Clues

Reversibility known to be important
[McLachlan and Perlmutter, 2006]
Most test problems integrable
(First integrals common evaluation criterion )

Notion: additional structure behind long-time behaviour

Strategy

Identify structure of standard nonholonomic test problems

Clues

Reversibility known to be important
[McLachlan and Perlmutter, 2006]
Most test problems integrable
(First integrals common evaluation criterion )

Energy

Time

DLA but nonreversible

DLA and reversible

Nonholonomically coupled systems

Definition: Nonholonomically Coupled System (NCS)

L(\mathbf x, \xi, \dot{\mathbf x},\dot\xi) = L_1(\mathbf x,\dot{\mathbf x}) + L_2(\xi,\dot\xi)

L(\mathbf x, \xi, \dot{\mathbf x},\dot\xi) = L_1(\mathbf x,\dot{\mathbf x}) + L_2(\xi,\dot\xi)

A(\xi)\dot{\mathbf x} = 0

A(\xi)\dot{\mathbf x} = 0

\displaystyle\frac{d}{dt}\frac{\partial L_2}{\partial\dot\xi} =\frac{\partial L_2}{\partial \xi}

\displaystyle\frac{d}{dt}\frac{\partial L_2}{\partial\dot\xi} =\frac{\partial L_2}{\partial \xi}

independent subsystem (driver)

\dot{\mathbf x} = \mathbf{k}(\xi) v \qquad \dot v= \mathbf{k}(\xi)\cdot \mathbf F(\mathbf x)

\dot{\mathbf x} = \mathbf{k}(\xi) v \qquad \dot v= \mathbf{k}(\xi)\cdot \mathbf F(\mathbf x)

Conserved energies: $E_1(\mathbf x,v)$ and $E_2(\xi,\dot\xi)$

Is system on $\mathcal M$ integrable?

Integrable NCS

\dot{\mathbf u} = B(\xi)\mathbf u

\dot{\mathbf u} = B(\xi)\mathbf u

$B(\xi)\in \mathfrak{g}\subset \mathfrak{gl}(n)$
( $\mathfrak{g}$ -system)

Definition: ODE system integrable $\iff$ Action-Angle variables

Theorem (M. and Verdier)

NCS (with additional assumptions) are fibrated over integrable system

Reduced dynamics

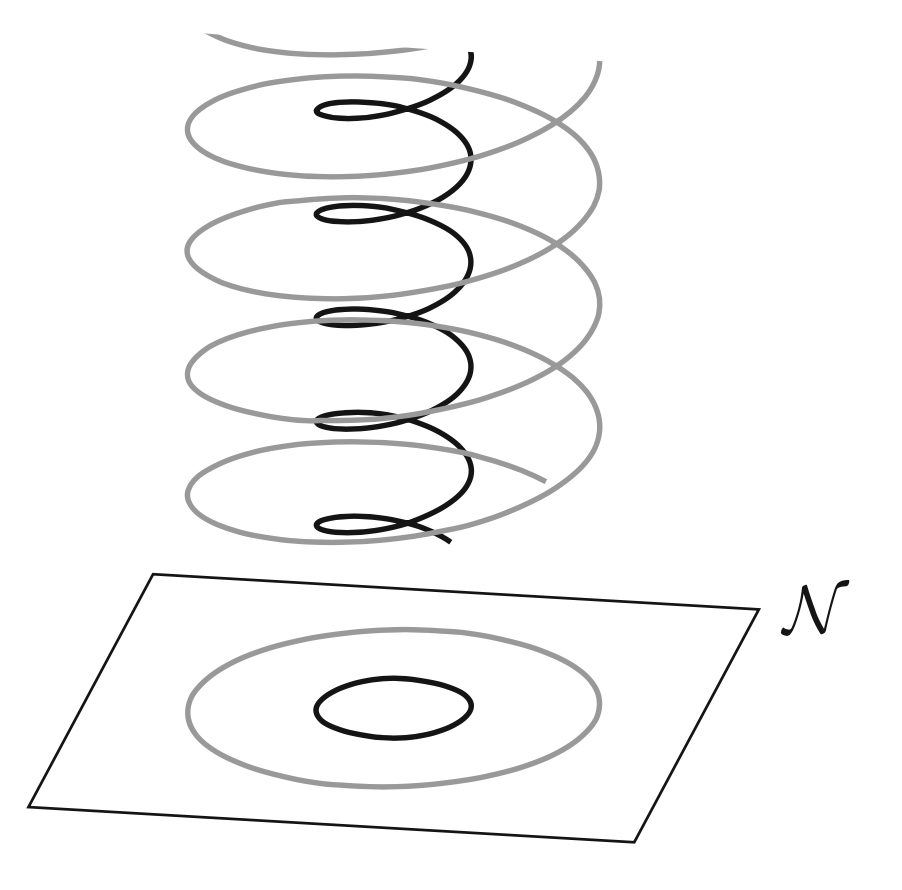
Next step: KAM theory

Requirement for KAM:

dynamics either symplectic or reversible

Exact flow:

(\mathbf q_0,\dot{\mathbf q}_0)\mapsto (\mathbf q(h),\dot{\mathbf q}(h))

(\mathbf q_0,\dot{\mathbf q}_0)\mapsto (\mathbf q(h),\dot{\mathbf q}(h))

\mathcal M \to \mathcal M

\mathcal M \to \mathcal M

\mathcal N \to \mathcal N

\mathcal N \to \mathcal N

Action-Angle variables

\mathcal N \to \mathcal N

\mathcal N \to \mathcal N

KAM stable tori

reversible perturbation

Discrete flow:

(\mathbf q_k,\dot{\mathbf q}_k)\mapsto (\mathbf q_{k+1},\dot{\mathbf q}_{k+1})

(\mathbf q_k,\dot{\mathbf q}_k)\mapsto (\mathbf q_{k+1},\dot{\mathbf q}_{k+1})

\mathcal M \to \mathcal M

\mathcal M \to \mathcal M

\approx

\approx

Next step: KAM theory

Requirement for KAM:

dynamics either symplectic or reversible

Exact flow:

(\mathbf q_0,\dot{\mathbf q}_0)\mapsto (\mathbf q(h),\dot{\mathbf q}(h))

(\mathbf q_0,\dot{\mathbf q}_0)\mapsto (\mathbf q(h),\dot{\mathbf q}(h))

\mathcal M \to \mathcal M

\mathcal M \to \mathcal M

\mathcal N \to \mathcal N

\mathcal N \to \mathcal N

Action-Angle variables

\mathcal N \to \mathcal N

\mathcal N \to \mathcal N

KAM stable tori

reversible perturbation

Discrete flow:

(\mathbf q_k,\dot{\mathbf q}_k)\mapsto (\mathbf q_{k+1},\dot{\mathbf q}_{k+1})

(\mathbf q_k,\dot{\mathbf q}_k)\mapsto (\mathbf q_{k+1},\dot{\mathbf q}_{k+1})

\mathcal M \to \mathcal M

\mathcal M \to \mathcal M

\approx

\approx

possible failure

Next step: KAM theory

Requirement for KAM:

dynamics either symplectic or reversible

Exact flow:

(\mathbf q_0,\dot{\mathbf q}_0)\mapsto (\mathbf q(h),\dot{\mathbf q}(h))

(\mathbf q_0,\dot{\mathbf q}_0)\mapsto (\mathbf q(h),\dot{\mathbf q}(h))

\mathcal M \to \mathcal M

\mathcal M \to \mathcal M

\mathcal N \to \mathcal N

\mathcal N \to \mathcal N

Action-Angle variables

\mathcal N \to \mathcal N

\mathcal N \to \mathcal N

KAM stable tori

reversible perturbation

Discrete flow:

(\mathbf q_k,\dot{\mathbf q}_k)\mapsto (\mathbf q_{k+1},\dot{\mathbf q}_{k+1})

(\mathbf q_k,\dot{\mathbf q}_k)\mapsto (\mathbf q_{k+1},\dot{\mathbf q}_{k+1})

\mathcal M \to \mathcal M

\mathcal M \to \mathcal M

\approx

\approx

possible failure

Theorem (M. and Verdier)

If discrete flow

Preserve fibration
Preserves reversibility (from action-angle variables)

then all integrals are nearly conserved

Next step: KAM theory

Requirement for KAM:

dynamics either symplectic or reversible

Exact flow:

(\mathbf q_0,\dot{\mathbf q}_0)\mapsto (\mathbf q(h),\dot{\mathbf q}(h))

(\mathbf q_0,\dot{\mathbf q}_0)\mapsto (\mathbf q(h),\dot{\mathbf q}(h))

\mathcal M \to \mathcal M

\mathcal M \to \mathcal M

\mathcal N \to \mathcal N

\mathcal N \to \mathcal N

Action-Angle variables

\mathcal N \to \mathcal N

\mathcal N \to \mathcal N

KAM stable tori

reversible perturbation

Discrete flow:

(\mathbf q_k,\dot{\mathbf q}_k)\mapsto (\mathbf q_{k+1},\dot{\mathbf q}_{k+1})

(\mathbf q_k,\dot{\mathbf q}_k)\mapsto (\mathbf q_{k+1},\dot{\mathbf q}_{k+1})

\mathcal M \to \mathcal M

\mathcal M \to \mathcal M

\approx

\approx

possible failure

Theorem (M. and Verdier)

If discrete flow

Preserve fibration
Preserves reversibility (from action-angle variables)

then all integrals are nearly conserved

Numerical verification

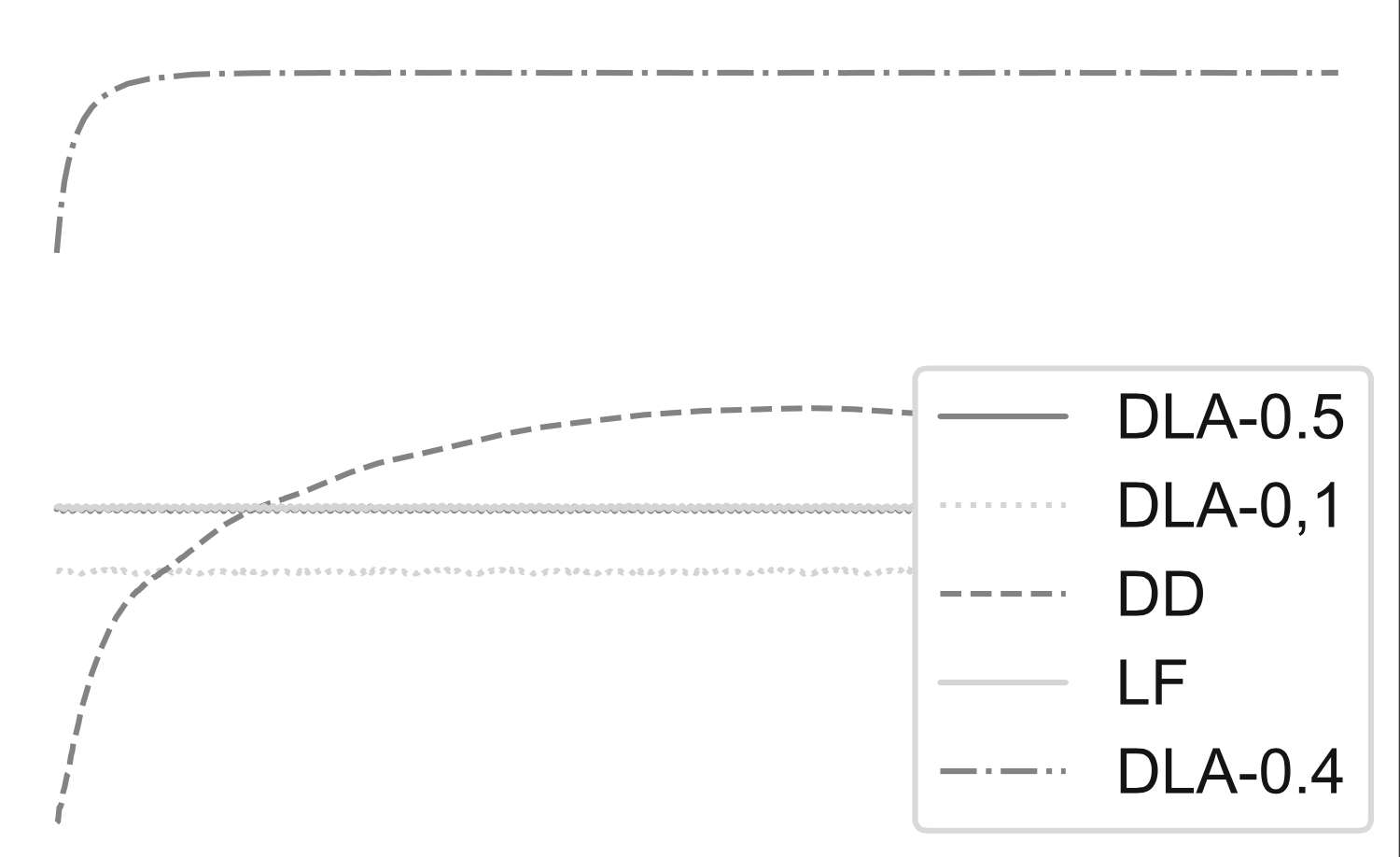
CVT problem

Sub-energy $E_1$

Time

Is the result sharp?

Strategy: construct NCS by perturbing

fibration projection
reversibility map

IMPORTANT: resulting systems are still integrable NCS

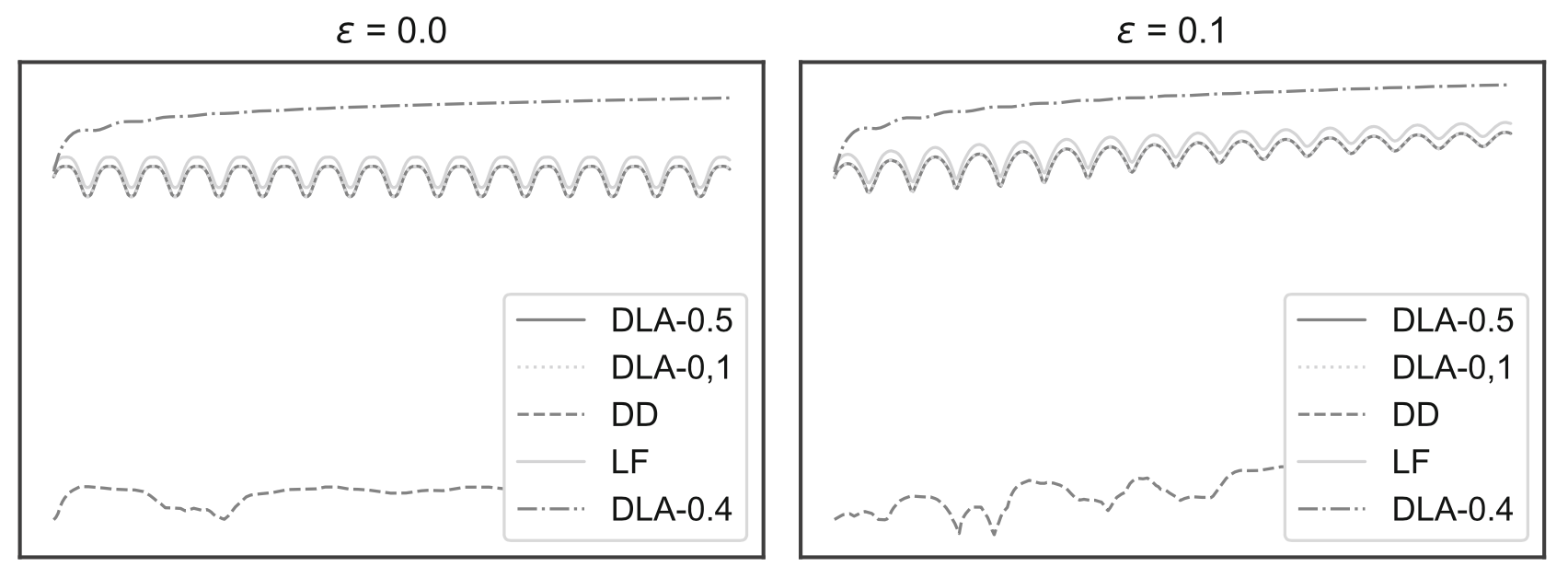
Knife edge, perturbed fibration

Total energy

Is the result sharp?

Strategy: construct NCS by perturbing

fibration projection
reversibility map

IMPORTANT: resulting systems are still integrable NCS

CVT, perturbed reversibility

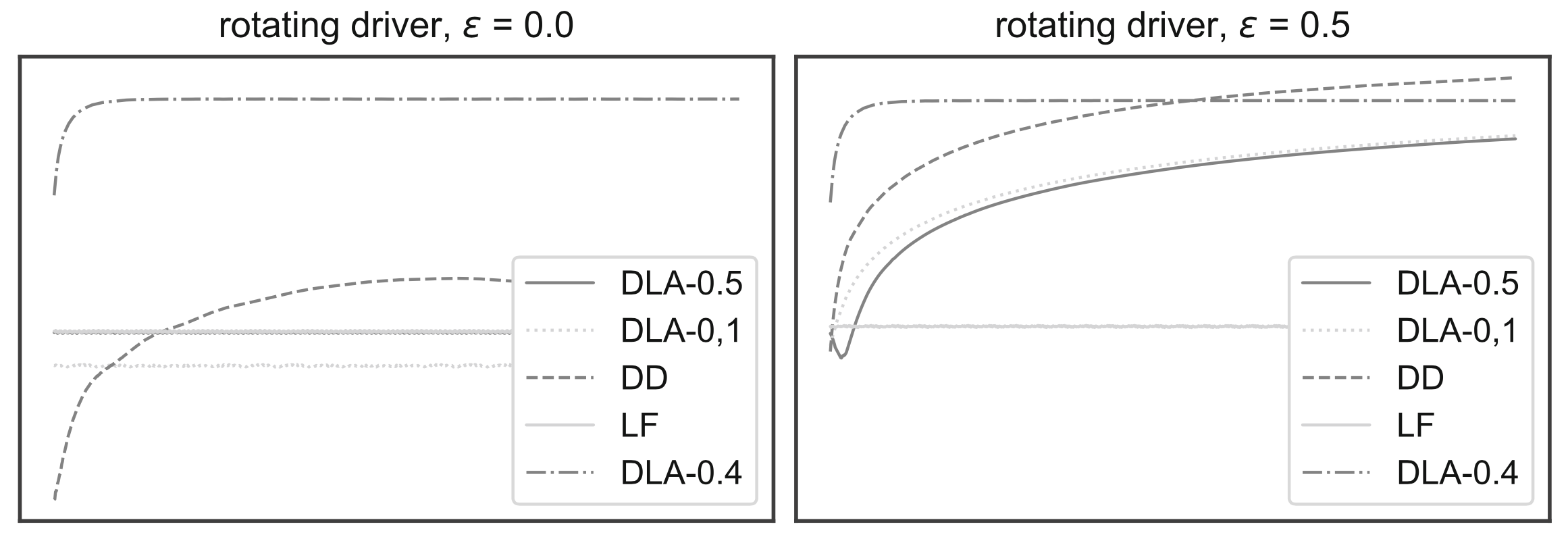
Sub-energy $E_1$

Conclusion and outlook

DLA does not imply structure preservation
Reason: class of nonholonomic systems too large for generic DLA approach
Strategy: focus on subclasses with enough structure for e.g. KAM (Hamiltonian or reversible)

Already started: recent work by [Martín de Diego et. al.]

THANKS!

Slides available at: slides.com/kmodin

What makes nonholonomic integrators work?

Klas Modin