Quantized hydrodynamics on the sphere

Klas Modin

 slides.com/kmodin

azimuth

2D Euler on the Sphere

elevation

\dot\omega - \{\psi,\omega \} = 0
\Delta\psi = \omega

Can statistical mechanics be used to explain clustering?

Idea by Onsager (1949):

  • Approximate \(\omega\) by PV for large \(N\)
  • Find invariant measure and presume ergodicity

Hamiltonian function:

\displaystyle H(x_1,\ldots,x_N) = -\sum_{kl} \Gamma_k\Gamma_l \log |x_1-x_N|

Onsager's observation:

Pos. and neg. strengths \(\Rightarrow\) energy takes values \(-\infty\) to \(\infty\)

\(\Rightarrow\) phase volume function \(V(E)\) has inflection point

Idea by Onsager (1949):

  • Approximate \(\omega\) by PV for large \(N\)
  • Find invariant measure and presume ergodicity

Hamiltonian function:

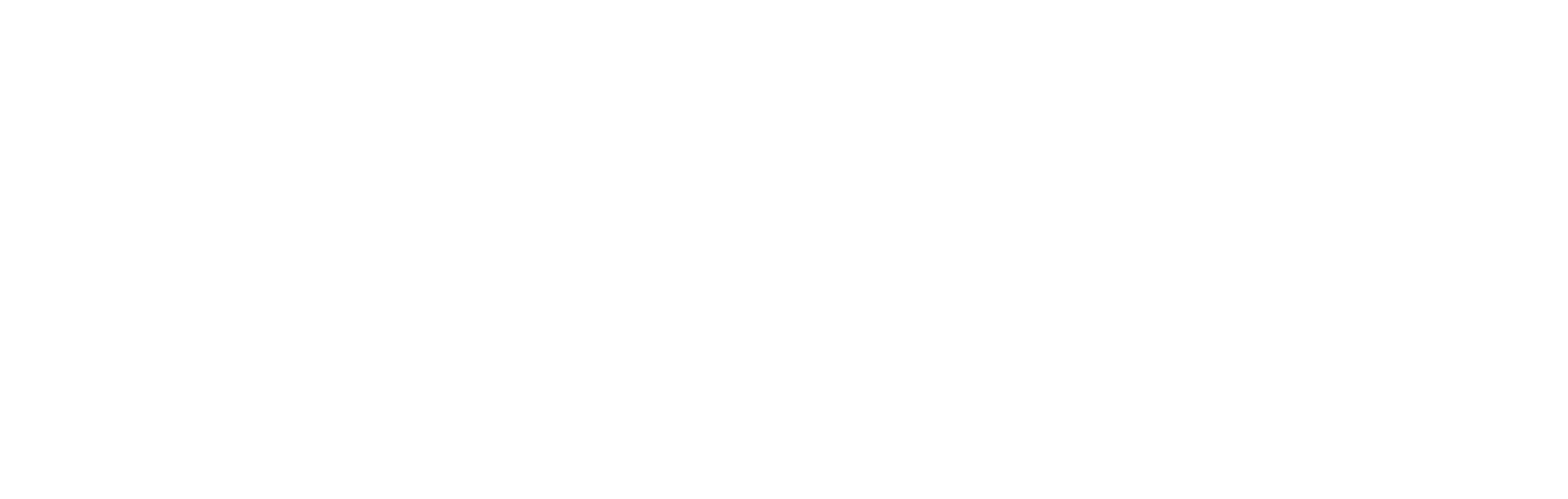
\displaystyle H(x_1,\ldots,x_N) = -\sum \Gamma_k\Gamma_l \log |x_1-x_N|

Can statistical mechanics be used to explain clustering?

Onsager's theory has problems

Quantization yields Lie-Poisson preserving discretizations

Zeitlin (1991)

Classical

Quantized

\omega \in C_0^\infty
W \in \mathfrak{su}(N)
\{\cdot,\cdot \}
[\cdot,\cdot ]
\dot\omega = \{\psi,\omega \}
\dot W = [P,W]

Zeitlin's equations

\dot W = [P,W],
\Delta_N P = W
P,W \in \mathfrak{su}(N)

vorticity matrix

stream matrix

Hoppe-Yau Laplacian

\displaystyle C^\infty_0(\mathbb{S}^2)\ni\omega \longrightarrow \sum_{l=0}^\infty\sum_{m=-l}^l \omega_{lm} Y_{lm} \longrightarrow \sum_{l=0}^N\sum_{m=-l}^l \omega_{lm} T_{lm} \in \mathfrak{su}(N)

Lost in translation: dictionary hydrodynamics \(\leftrightarrow\) quantum physics

Classical Quantum
Lie group
Lie algebra
Phase space
"Strong" norm
Enstrophy norm
Energy norm
Measurables
Singular sol. vortex sheets rank-1 matrices
Axi-symmetry

 \(\operatorname{SDiff}(\mathbb{S}^2)\)

 \(\operatorname{SU}(N)\)

 \(\mathfrak{X}_\mu(\mathbb{S}^2)\)

 \(C^\infty_0(\mathbb{S}^2)\)

 \(\mathfrak{su}(N)\)

 \(\mathfrak{su}(N)^*\simeq \mathfrak{su}(N)\)

 \(\lVert \cdot\rVert_{L^\infty}\)

spectral norm

 \(\lVert \cdot\rVert_{L^2}\)

Frobenius norm

 \(\lVert \cdot\rVert_{H^{-1}}\)

 \(\operatorname{tr}(PW)^{1/2}\)

values of \(\omega\)

eigenvalues of \(W\)

\(\omega\) zonal

\(W\) diagonal

azimuth

elevation

Long-time dynamics look like

"blob"-vortex dynamics

positive blobs

negative blobs

Are there low dim, near integrable stable invariant manifolds?

  1. Small vorticity formations merge to larger
  2. Well-separated blobs interact by blob-vortex dynamics (BVD)
  3. Dynamics is not integrable \(\Rightarrow\) blobs continue to merge
  4. \(k\)-BVD integrable \(\Rightarrow\) quasi-periodicity prevents further mixing

Shnirelman (2005)

Question 1: How can merging occur when vorticity is transported?

  • Arnold (1966): \(\omega(t) = \varphi^t_*\omega(0) \) for \(\varphi^t\in\operatorname{SDiff}(\mathbb{S}^2)\)
  • Izosimov, Khesin, Mousavi  (2016): Orbits of simple Morse functions = Reeb graphs

Euler's equations (2D):

Zeitlin's equations:

  • \(W(t) = E(t)W(0) E(t)^\dagger \) for \(E(t) \in SU(N) \)
  • Spectral theorem: orbits = diagonal matrices with increasing eigenvalues
  • Diagonal = zonal \(\rightarrow\) possible to destroy critical points \(\rightarrow\) merging possible (but "hard")

Zeitlin's equations describe generalized hydrodynamics

Shnirelman (1993)

\mathcal{O}_{\omega_0} = L^\infty \text{ weak* closure of } \omega_0\circ\operatorname{SDiff}(\mathbb{S}^2)

Bordemann, Meinrenken, Schlichenmaier (1994)

\(W \to \omega\) in weak* sense as \(N\to \infty\)

Question 2: Is blob vortex

dynamics integrable?

Dirac \(\delta_x\)

x
x
\delta_x
b_x
\displaystyle H = -\sum \Gamma_k\Gamma_l \log |x_k-x_l|
\displaystyle H = -\frac{1}{2}\sum \langle b^l_{x_l},\Delta^{-1} b^k_{x_k}\rangle

axisymmetric blob \(b_x\) centered at \(x\)

Same \(SO(3)\) symmetry!

Known about integrability

Point vortex dynamics on \(\mathbb{S}^2\)

  • 3-PVD is integrable (Sakajo, 1999)
  • 4-PVD is integrable for vanishing momentum (Sakajo, 2007)
  • 4-PVD non-integrable in general (Bagrets & Bagrets, 1997)

Symplectic reduction theory:

only \(SO(3)\) symmetry needed in proof

\Rightarrow

Blob vortex dynamics on \(\mathbb{S}^2\)

  • 3-BVD is integrable
  • 4-BVD is integrable for vanishing momentum

Proposed mechanism under scrutiny

Non-zero angular momentum

passed 1st test!

Question 3: Are BVD solutions stable within Euler flow?

  • Clearly BV profiles change dynamically
  • Initially small perturbation
  • Remains small?

?

  • Strategy: study dynamics on \( (\mathfrak{su}(2)\times \mathfrak{su}(N))^k\)
t = 0
t = \epsilon

small w.r.t.

\(H^{-1}\) or \(L^2\)

or what?

Question 4: Is there a natural way to separate scales?

Underlying notion: quantization yields canonical vorticity splitting

 

  1. Linear subspace \(\operatorname{stab}_P = \operatorname{ker}[P,\cdot]\subset \mathfrak{su}(N)\)
  2. Project \(\Pi_P:W\mapsto W_s\in\operatorname{stab}_P\)
  3. Gives canonical splitting \( W = W_s + W_r\)
W
W_s
\operatorname{stab}_P
W_r

Evolution of canonical components

t = 0
t = \text{large}
W
W_s
W_r

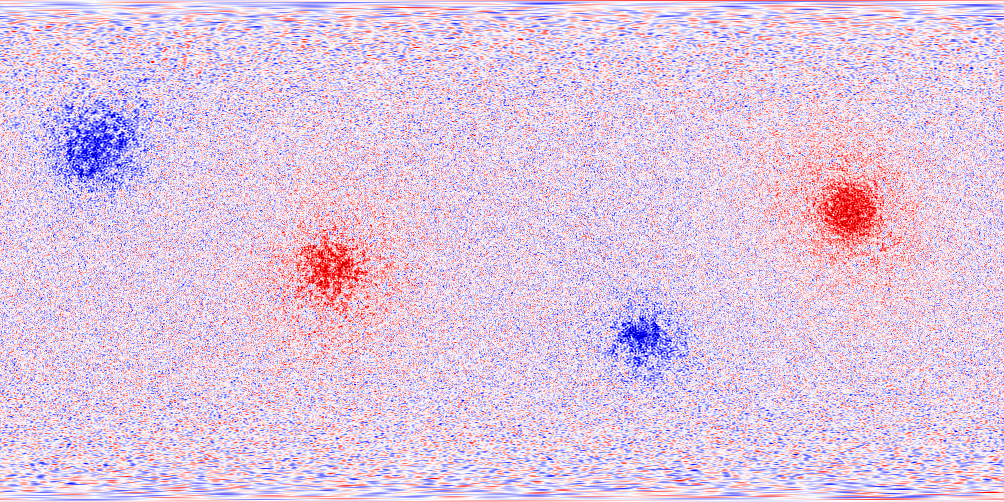
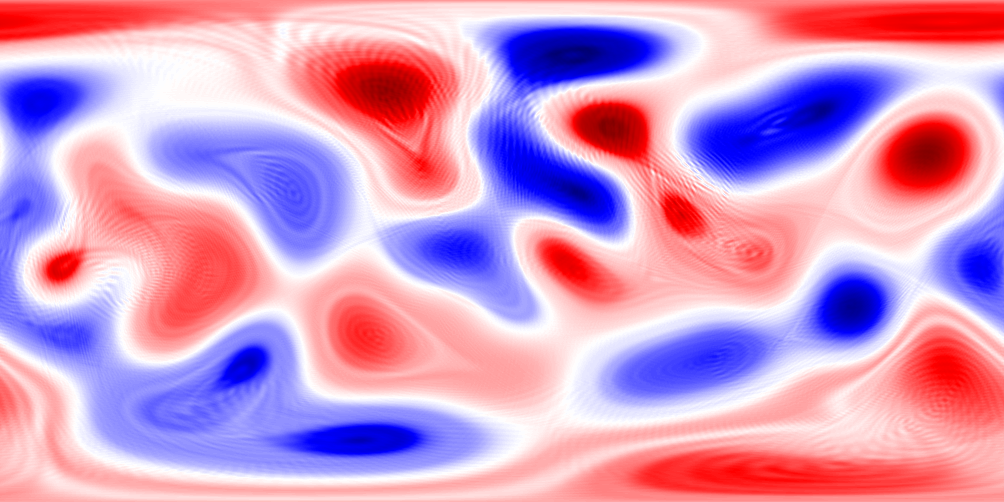
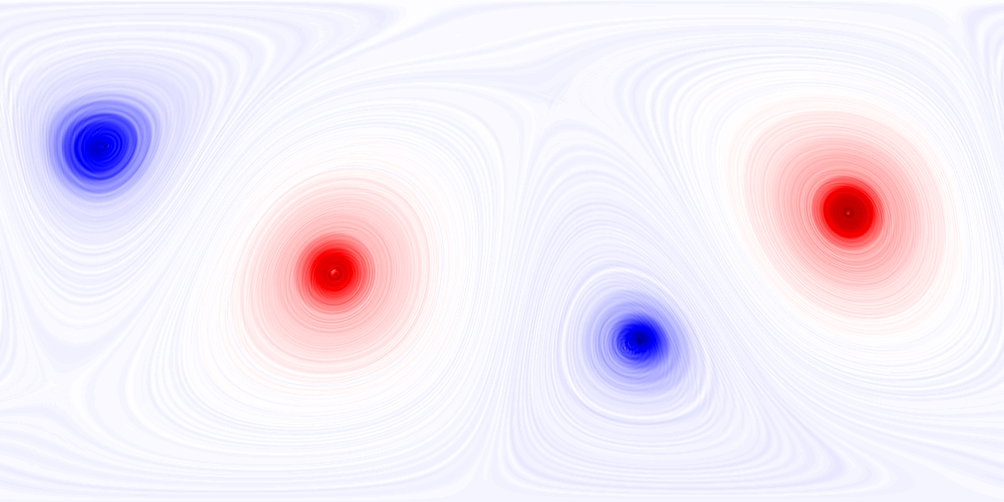
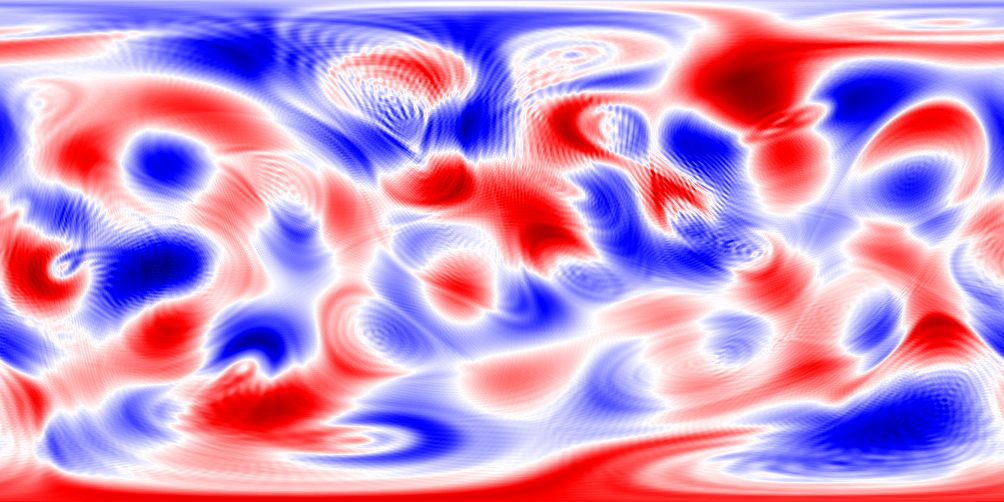
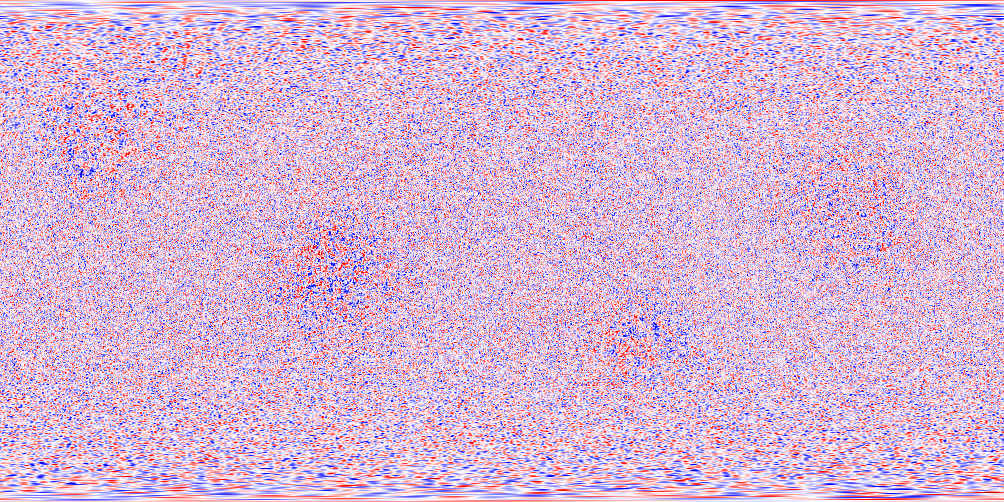
Enstrophy for canonical components

E
0
E_r
t
E_s

Enstrophies:

\(E = \langle W,W\rangle_F\)       \(E_s = \langle W_s,W_s\rangle_F\)        \(E_r = \langle W_r,W_r\rangle_F\)

E = E_s + E_r

Energy for canonical components

H
0
H_r
t
H_s

Energies:

\(H = \langle W,\Delta_N^{-1}W\rangle_F\)       \(H_s = \langle W_s,\Delta_N^{-1}W_s\rangle_F\)        \(H_r = \langle W_r,\Delta_N^{-1}W_r\rangle_F\)

H_s = H + H_r

Geometry of enstrophy and energy

W
W_s
W_r

\(W_r \bot W_s\) in enstrophy norm

\(W_r \bot W\) in energy norm

enstrophy levelset of \(W\)

energy levelset of \(W\)

\frac{1}{N}\lVert W_r\rVert_{E} \leq \lVert W_r \rVert_{H}

Equivalence of norms:

We expect Zeitlin's

model to be "grainy"

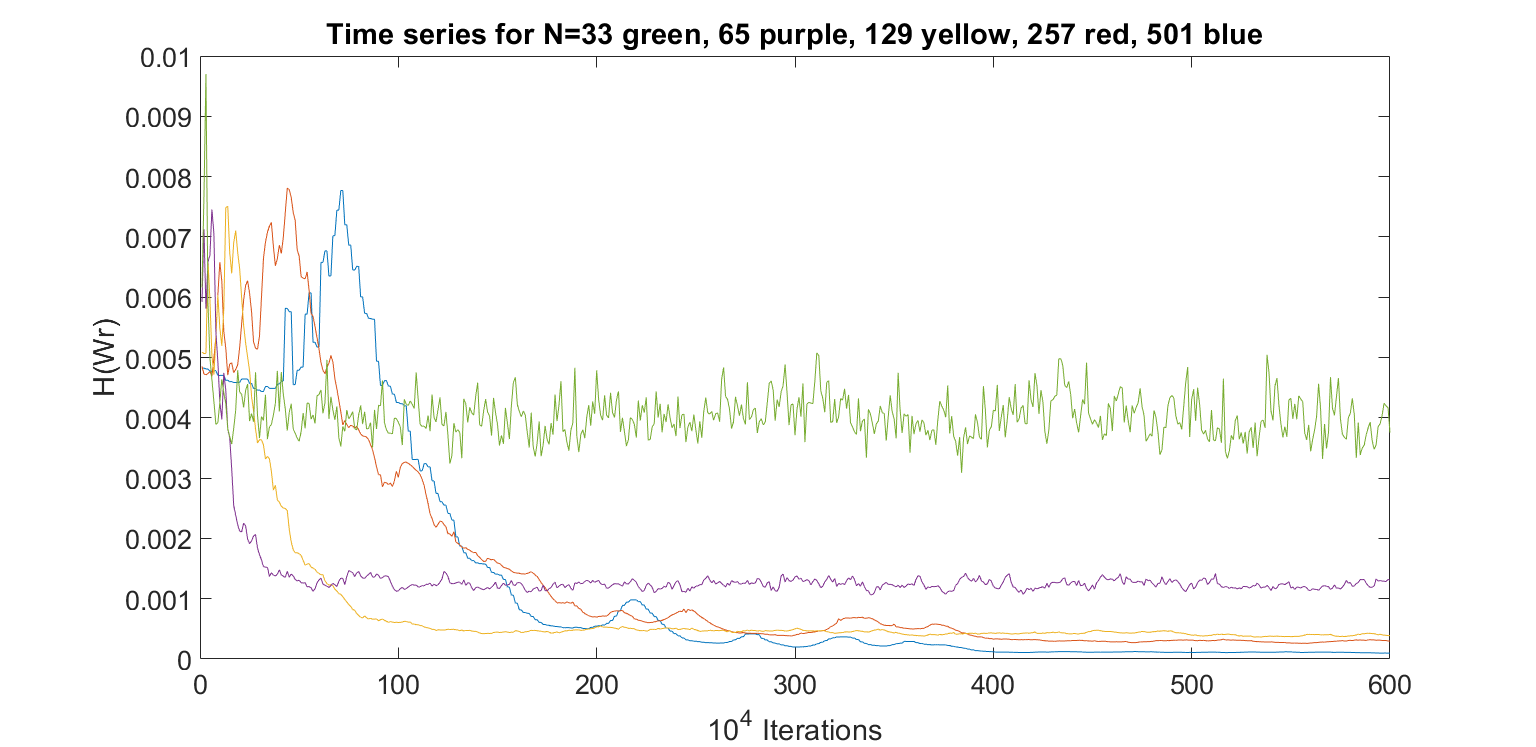
Canonical components capture "broken line" energy spectrum

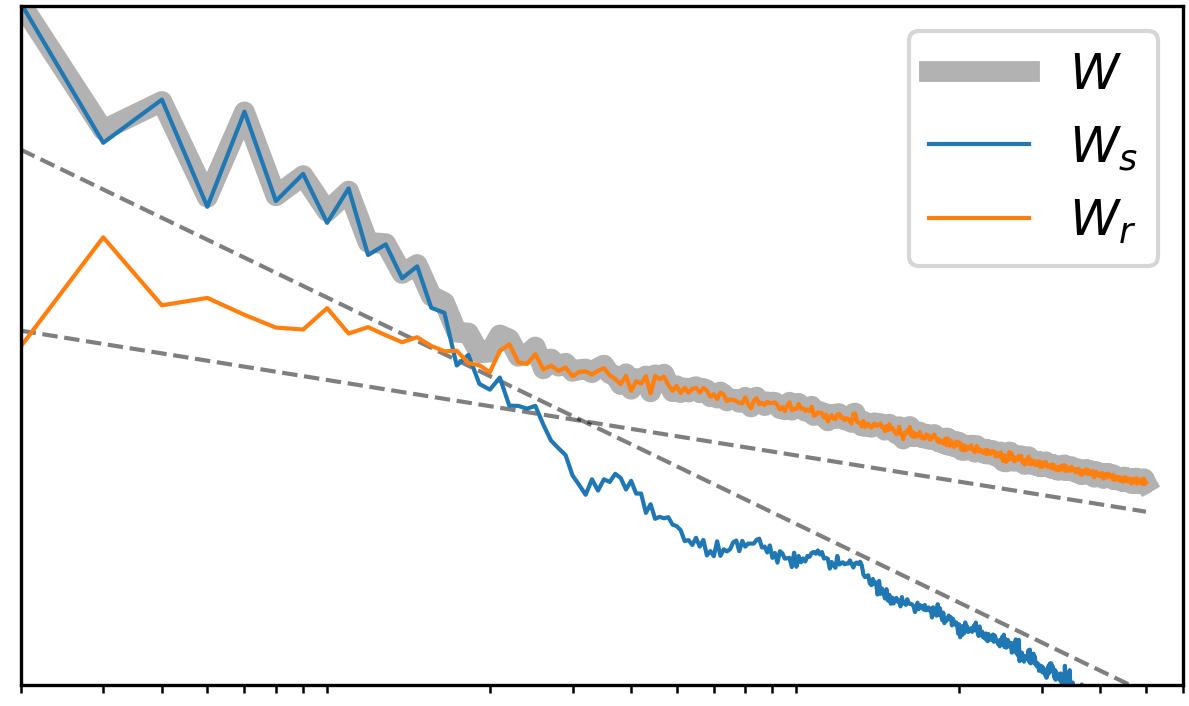
Summary: Zeitlin's model might yield useful insights on long-time dynamics for 2D Euler

References:

  • M. & Viviani (2021)
    Canonical scale separation in two-dimensional incompressible hydrodynamics
  • M. & Viviani (2021)
    Integrability of point-vortex dynamics via symplectic reduction: a survey
  • M. & Viviani (2020)
    A Casimir preserving scheme for long-time simulation of spherical ideal hydrodynamics
  • M. & Viviani (2020)
    Lie-Poisson methods for isospectral flows

Slides available at: slides.com/kmodin