Numerical integration

of classical spin systems

Presentation by Klas Modin

UppASD Autumn School 2022

Motivation

Elastic pendulum, slightly damped

Which integrators preserve qualitative long-time behaviour?

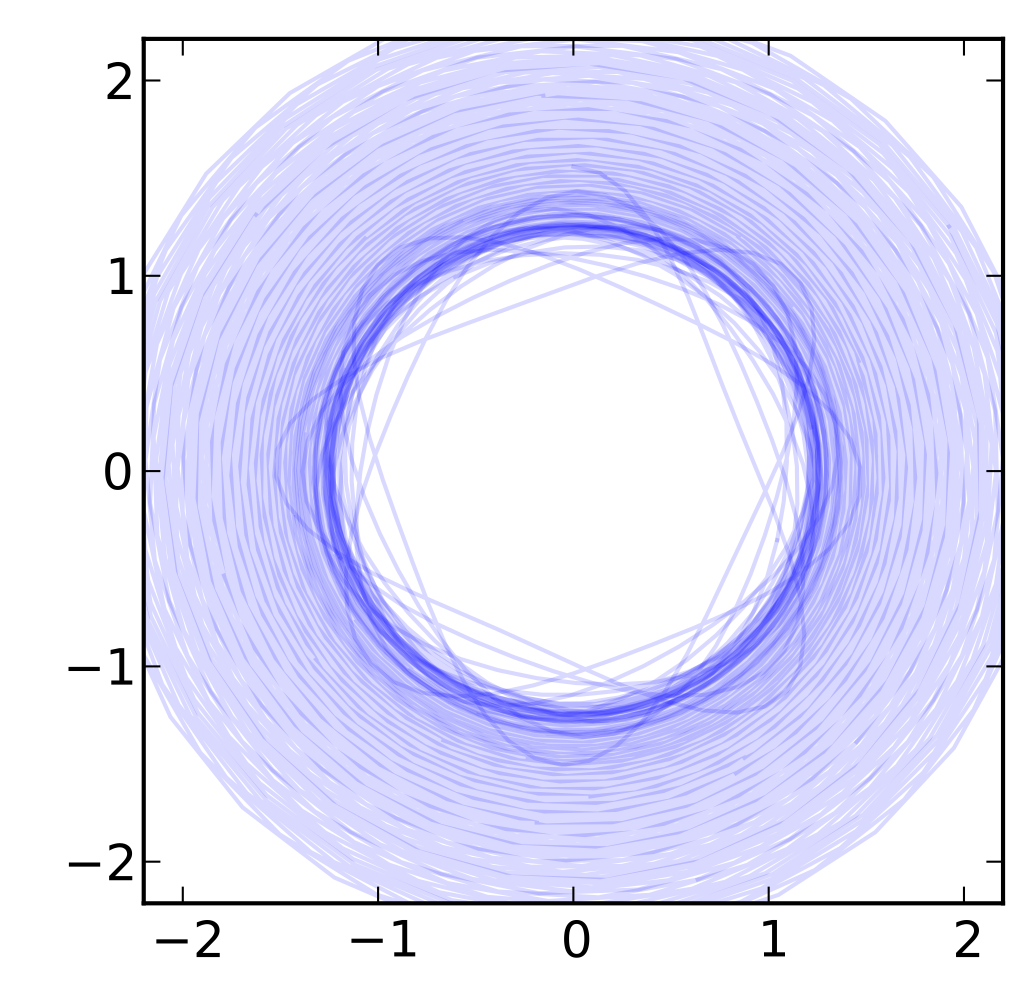
Heun's method

(2nd order accurate)

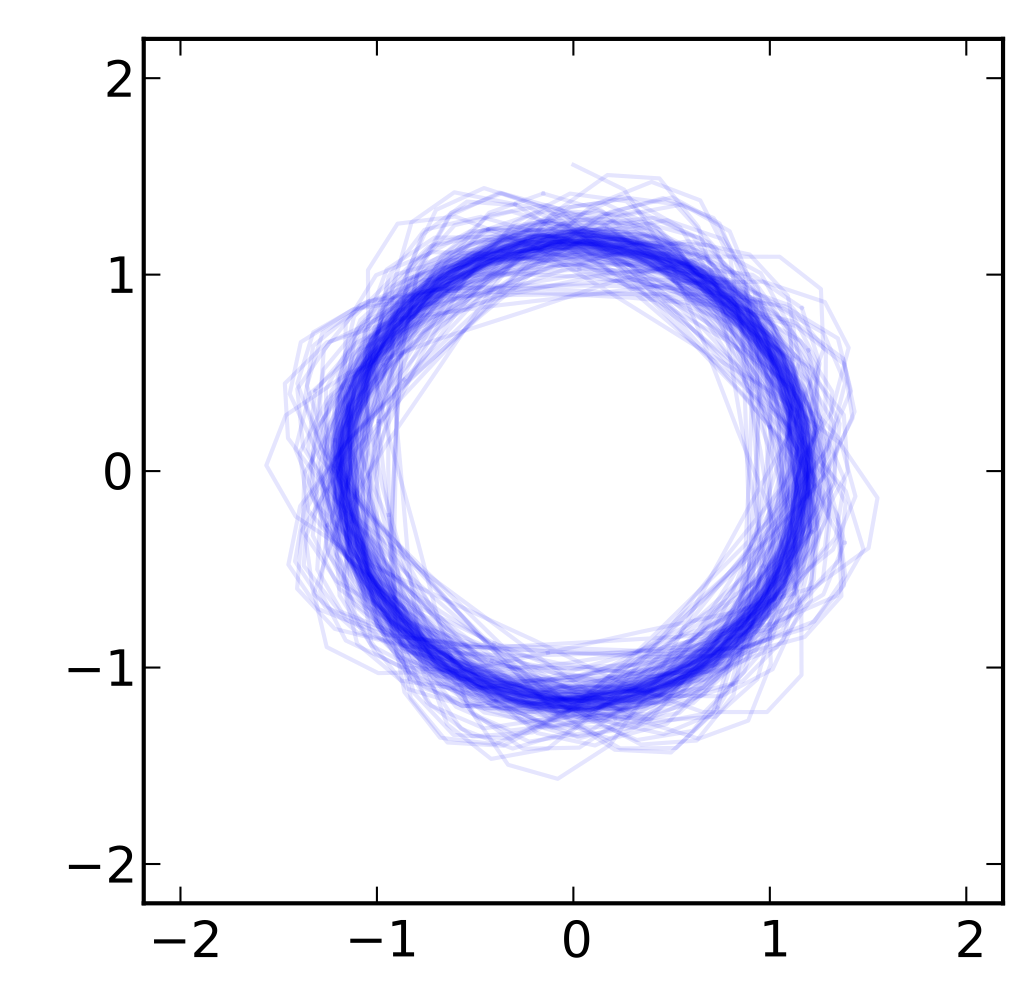
"Geometric" method

(2nd order accurate)

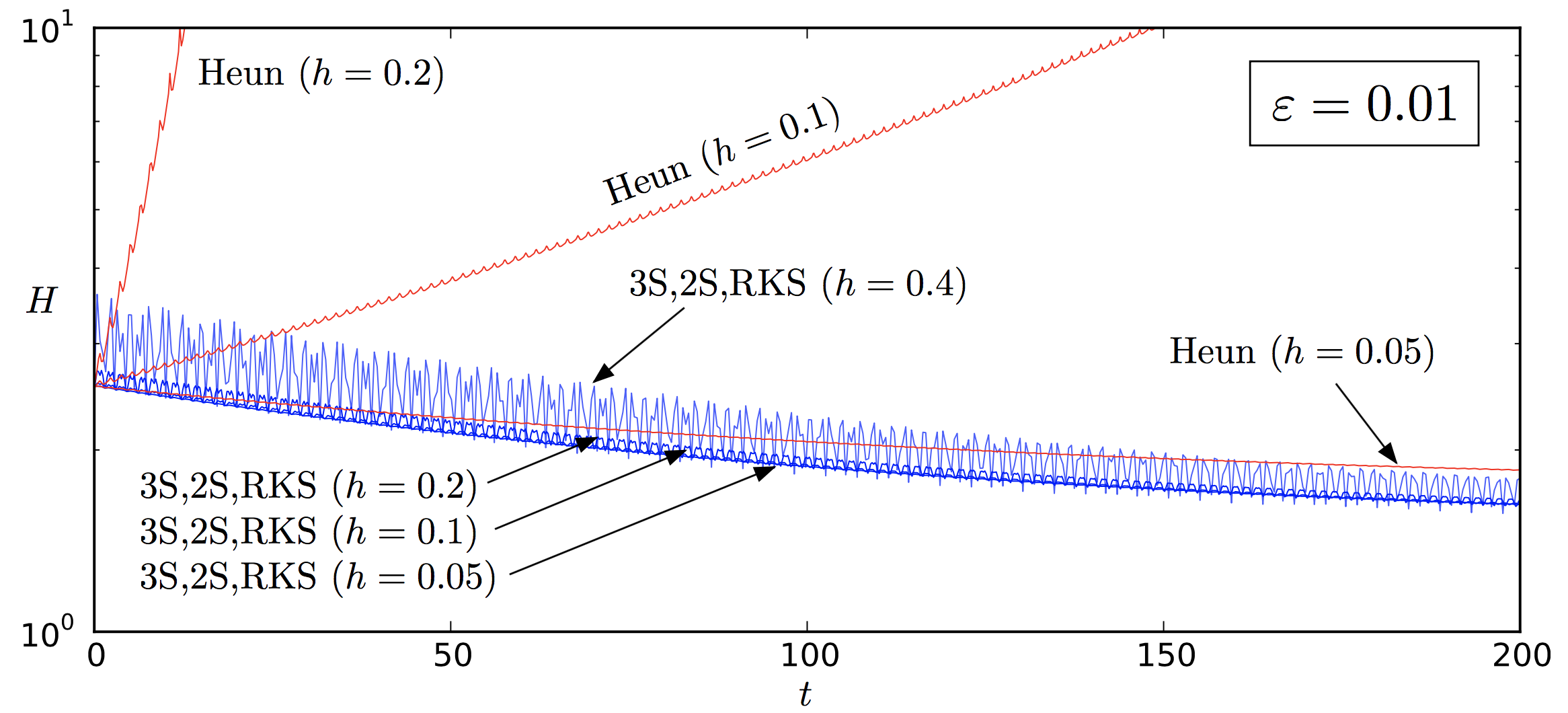
Why?

Total energy over time

Long-time trajectories for geometric method

Motto: discretized system should retain geometric structure

Outline

  • Classical spin systems
  • Hamiltonian structure and symplecticness
  • Review and comparison of numerical methods

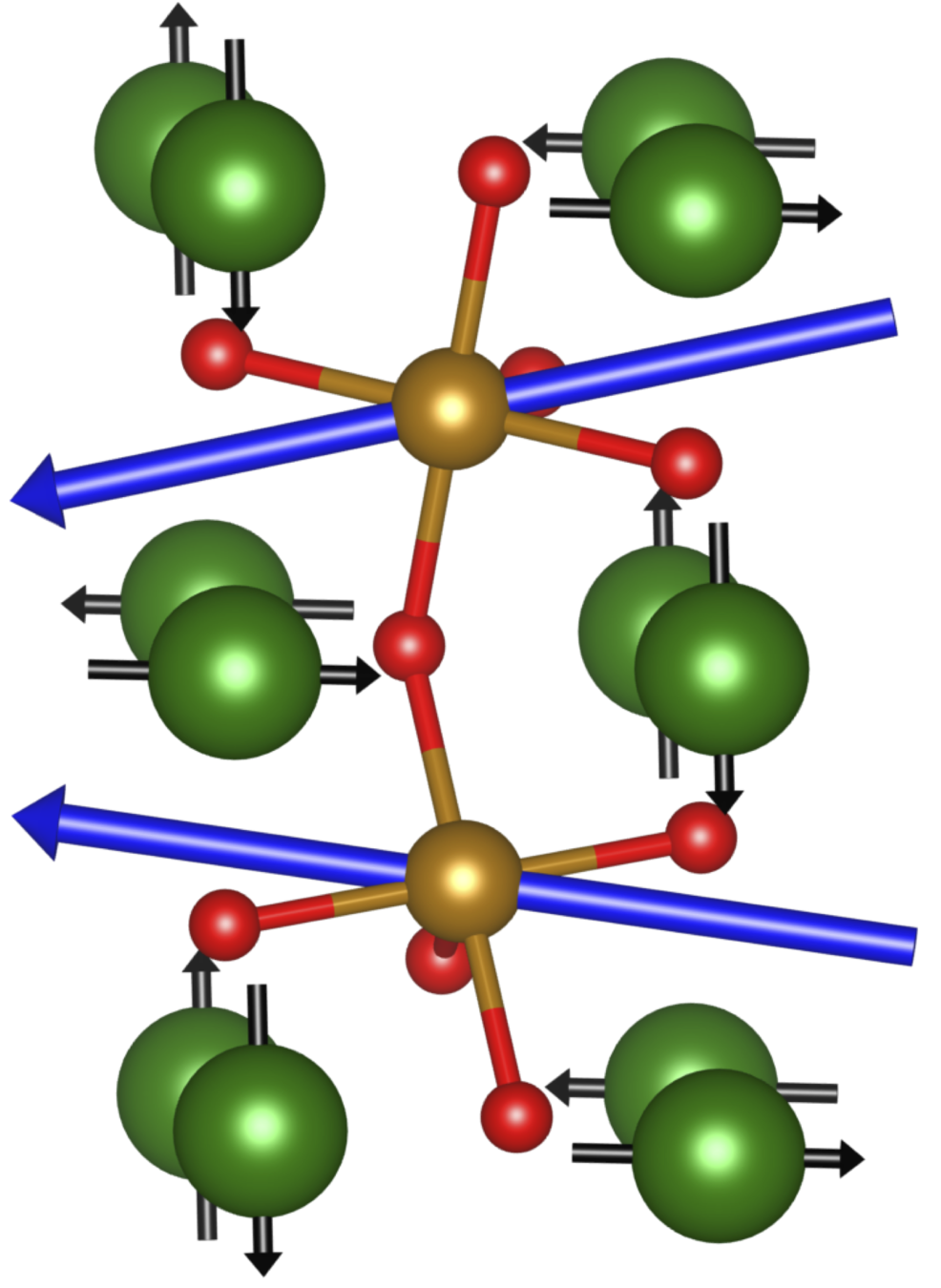
Classical spin systems

\displaystyle \dot{\mathbf{s}}_i = \mathbf{s}_i\times \nabla_{\mathbf{s}_i} H(\mathbf{s}_1,\ldots,\mathbf{s}_n) + f(\mathbf{s}_1,\ldots,\mathbf{s}_n, \dot{{W}})

Phase space \((S^2)^n\)

+\cdots +
\mathbf{s}_i = (s^x_i,s^y_i,s^z_i)\in S^2\subset \mathbb{R}^3

Hamiltonian

Non-conservative

Noise

Conservation laws

Spin lengths: \(\lVert \mathbf{s}_i \rVert = \) const

\displaystyle\frac{d}{dt} \lVert \mathbf{s}_i\rVert^2 = 2\, \mathbf{s}_i\cdot \dot{\mathbf{s}}_i = 2\, \mathbf{s}_i\cdot (\mathbf{s}_i\times \nabla_{\mathbf{s}_i}H) = 0

Total energy: \(H(\mathbf{s}_1,\ldots,\mathbf{s}_n) = \) const

\displaystyle\frac{d}{dt} H = \sum_{i=1}^n \nabla_{\mathbf{s}_i} H \cdot \dot{\mathbf{s}}_i = \sum_{i=1}^n \nabla_{\mathbf{s}_i} H\cdot (\mathbf{s}_i\times \nabla_{\mathbf{s}_i}H) = 0

Single-spin system: rigid body

H(\mathbf s) = \mathbf s\cdot \mathbb{I}^{-1}\mathbf s

moments of inertia tensor

angular momentum

Single-spin system: rigid body

Conservation of energy: \(\mathbf{s}\cdot \mathbb{I}^{-1}\mathbf{s}\) = const

Conservation of total momentum: \(\lVert\mathbf{s}\rVert^2\) = const

Many-spin system: Heisenberg chain

H(\mathbf s_1,\ldots,\mathbf s_n) = J\sum_i \mathbf s_i\cdot \mathbf s_{i+1}

coupling constant

Are there other conservation laws?

 Symplectic structure on \(S^2\) \[\Omega_\mathbf{s}(\mathbf u,\mathbf v)=\mathrm{det}(\mathbf s,\mathbf u,\mathbf v)\]

\mathbf s
\mathbf v
\mathbf u

Symplectic flow:

infinitesimal area preserved in time

A
\varphi^t(A)

Are there other conservation laws?

 Symplectic structure on \((S^2)^n\) \[\Omega_{(\mathbf{s}_1,\ldots,\mathbf{s}_n)}(\mathbf u_1,\ldots,\mathbf u_1,,\mathbf v_1,\ldots,\mathbf v_n)=\sum_i\mathrm{det}(\mathbf s_i,\mathbf u_i,\mathbf v_i)\]

\mathbf s_1
\mathbf v_1
\mathbf u_1

\(+\cdots+\)

\mathbf s_n
\mathbf v_n
\mathbf u_n

What is a numerical integrator?

Exact flow:

(\mathbf s_1(t),\ldots,\mathbf s_n(t)) = \varphi^t(\mathbf s_1(0),\ldots,\mathbf s_n(0))

flow map

Numerical flow:

\Phi_h(\mathbf s_1,\ldots,\mathbf s_n) \approx \varphi^h(\mathbf s_1,\ldots,\mathbf s_n)

integrator map

Symplectic integrator

Symplectic integrator: \(\Phi_h\) preserves symplectic area form \(\Omega\)

A
\varphi^h(A)
\Phi_h(A)

But what does symplecticity entail?

Integrator \(\Phi_h\) symplectic \(\iff\) \(\Phi_h\) exact flow for modified Hamiltonian \(\tilde H_h\)

\(\Phi_h(\mathbf s_1,\ldots,\mathbf s_n) = \varphi_{\tilde H_h}^h(\mathbf s_1,\ldots,\mathbf s_n)\)

Consequences of symplecticness

This explains why symplectic integrators are superior!

  • "Almost" conservation of tori for Hamiltonian perturbations of integrable systems (KAM theory)
     
  • Convergence towards correct macroscopic equilibrium (e.g. temperature in MD)

Examples of integrators

Heun's method

\displaystyle {\mathbf s}_i^{k+1} = \mathbf s_i^{k} + \frac{h}{2}(\mathbf f_i + \tilde{\mathbf f}_i)
\mathbf f_i = \mathbf s_i^{k}\times \nabla_{\mathbf s_i} H( \mathbf s_1^{k},\ldots, \mathbf s_n^{k})
\tilde\mathbf f_i = (\mathbf s_i^{k}+h\mathbf f_i)\times \nabla_{\mathbf s_i} H( \mathbf s_1^{k}+h\mathbf f_1,\ldots, \mathbf s_n^{k}+h\mathbf f_n)

Spherical midpoint method

\displaystyle\frac{\mathbf s^{k+1}_i - \mathbf s^{k}_i}{h} = \frac{\mathbf s^{k+1}_i+\mathbf s^{k}_i}{|\mathbf s^{k+1}_i+\mathbf s^{k}_i|}\times \nabla_{\mathbf s_i} H\left(\frac{\mathbf s^{k+1}_1+\mathbf s^{k}_1}{|\mathbf s^{k+1}_1+\mathbf s^{k}_1|},\ldots, \frac{\mathbf s^{k+1}_n+\mathbf s^{k}_n}{|\mathbf s^{k+1}_n+\mathbf s^{k}_n|} \right)

Midpoint method

\displaystyle\frac{\mathbf s^{k+1}_i - \mathbf s^{k}_i}{h} = \frac{\mathbf s^{k+1}_i+\mathbf s^{k}_i}{2}\times \nabla_{\mathbf s_i} H\left(\frac{\mathbf s^{k+1}_1+\mathbf s^{k}_1}{2},\ldots, \frac{\mathbf s^{k+1}_n+\mathbf s^{k}_n}{2} \right)

Properties

Heun Midpoint Spherical midpoint
Explicit yes no no
Spin lengths no yes yes
Energy no if quadratic modified
Symplectic no no yes

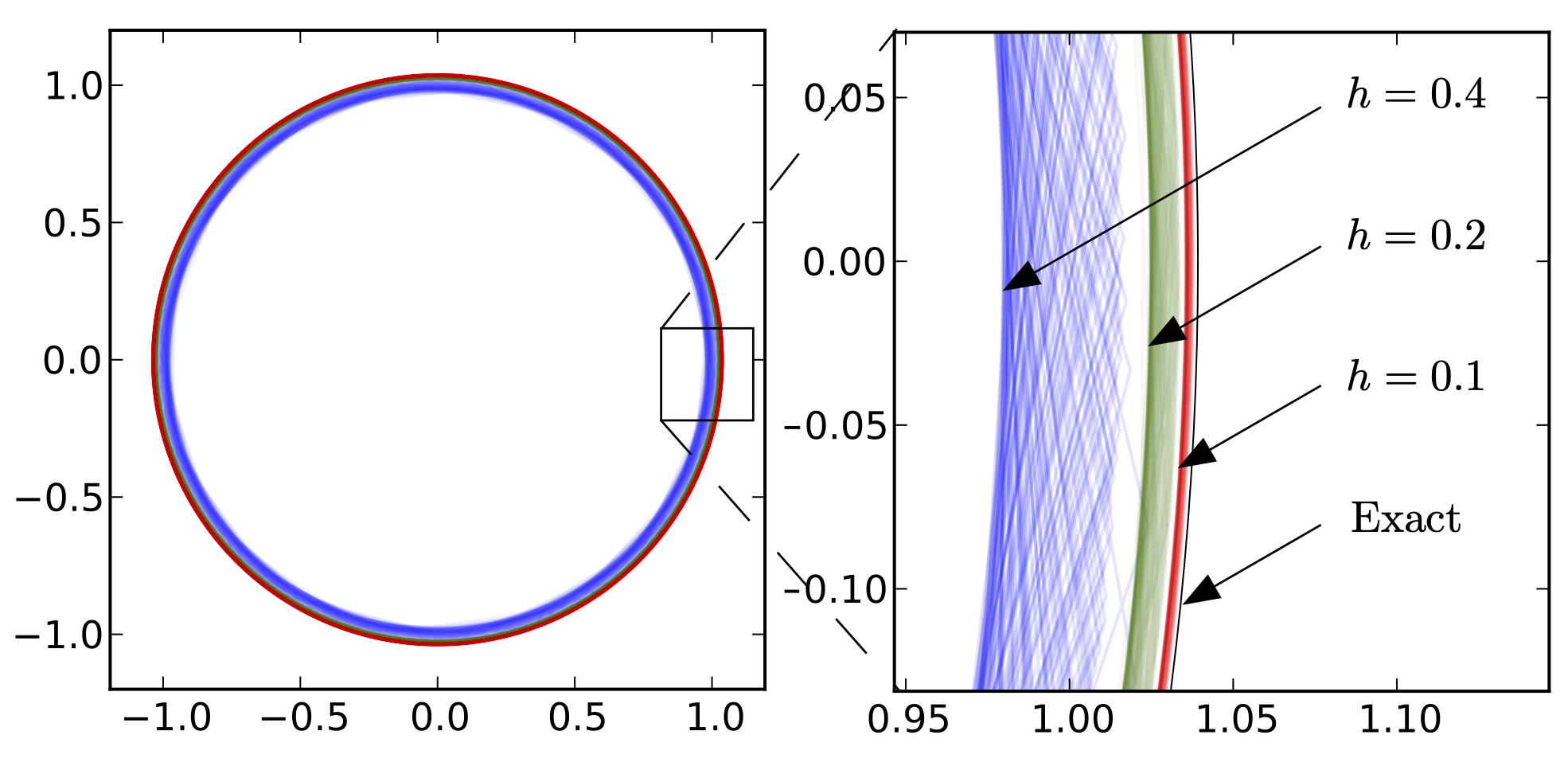
Example 1: rigid body

H(\mathbf s) = \mathbf s\cdot \mathbb{I}^{-1}\mathbf s

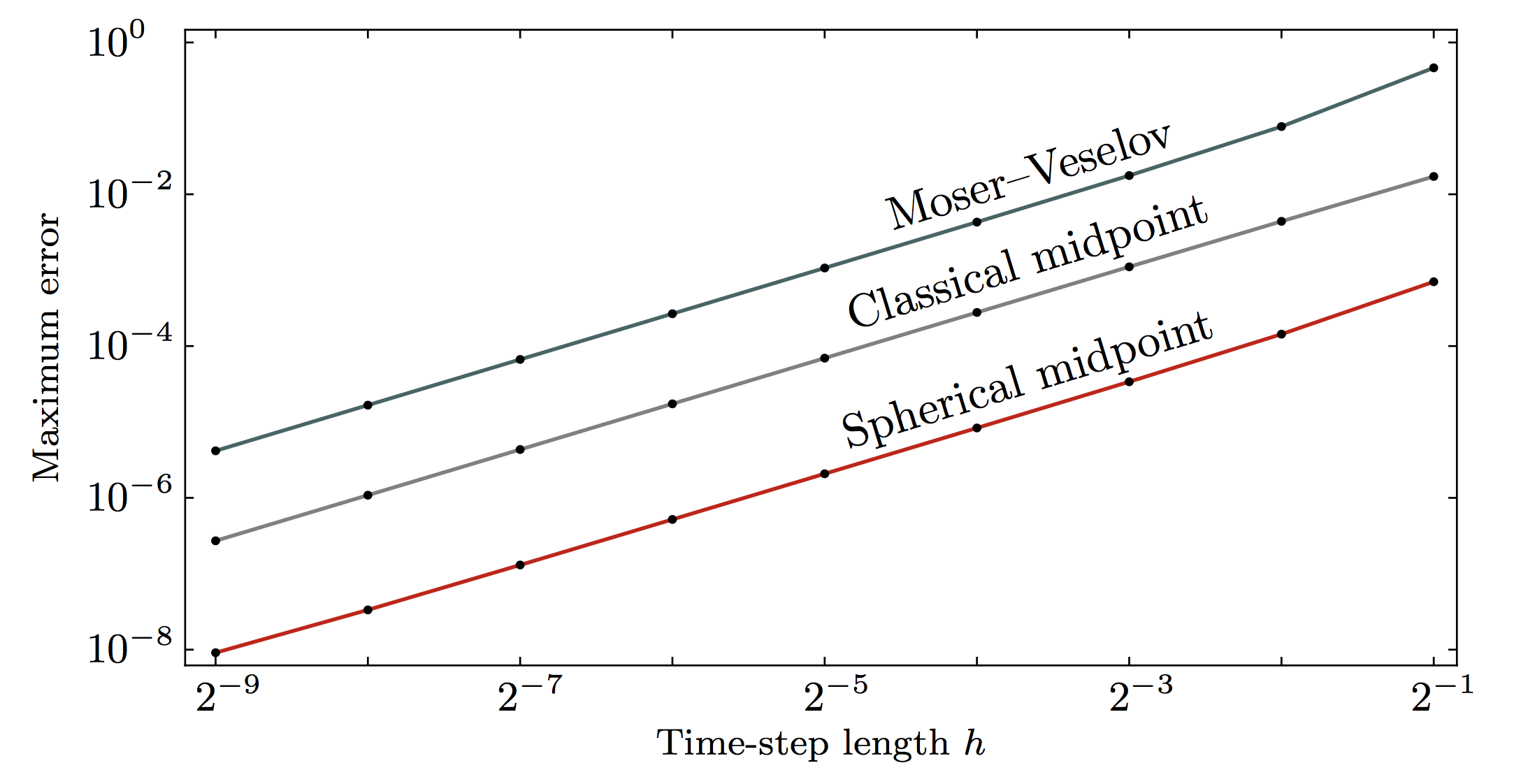
Example 2: complicated single spin

H(\mathbf s) = \mathbf s\cdot \mathbb{I}(\mathbf s)^{-1}\mathbf s
H(t)-H(0)

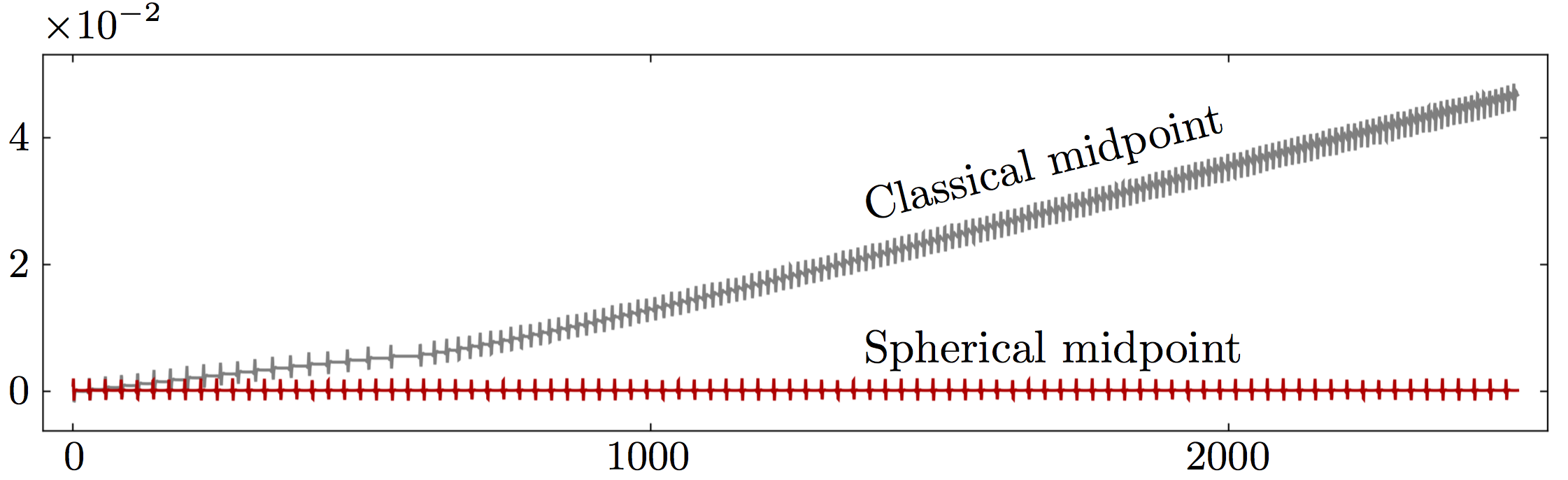
steps

Example 3: development of chaos

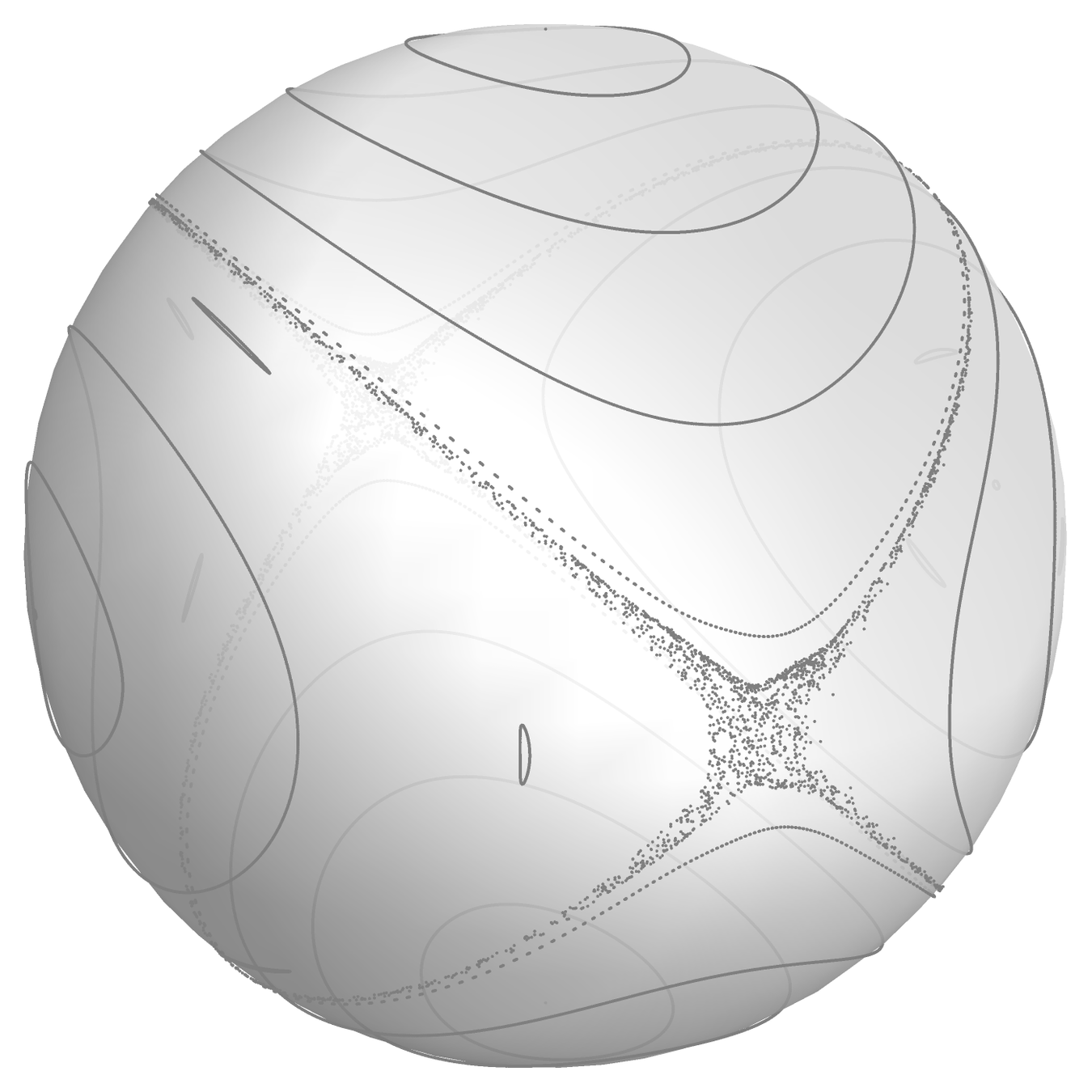
H(\mathbf s)= \frac{1}{2} \mathbf s\cdot \mathbb{I}^{-1}\mathbf s + \varepsilon \sin(t)s^x

Problem with implicit methods

Fix-point iterations or Newton iterations needed \(\Rightarrow\) intractable for large systems (too expensive)

Semi-implicit midpoint method  

\displaystyle\frac{\tilde{\mathbf s}^{k+1}_i - \mathbf s^{k}_i}{h} = \frac{\tilde{\mathbf s}^{k+1}_i+\mathbf s^{k}_i}{2}\times \nabla_{\mathbf s_i} H\left(\mathbf s^{k+1}_1,\ldots, \mathbf s^{k}_n\right)

[Mentink et al, 2010]

\displaystyle\frac{\mathbf s^{k+1}_i - \mathbf s^{k}_i}{h} = \frac{\mathbf s^{k+1}_i+\mathbf s^{k}_i}{2}\times \nabla_{\mathbf s_i} H\left(\frac{\tilde{\mathbf s}^{k+1}_1+\mathbf s^{k}_1}{2},\ldots, \frac{\tilde{\mathbf s}^{k+1}_n+\mathbf s^{k}_n}{2} \right)

Interpretation: two iterations for midpoint method

Symplectic no
Explicit yes
Spin lengths yes
Energy no (mostly)

Summary

  • Don't use "off-the-shelf" methods (Heun, RK, ...)
     
  • Correct phase space geometry affects qualitative long-time behavior more than local accuracy
    (no need for high order methods)
     
  • Qualitatively, symplectic methods always best
    (also for slightly damped systems)
     
  • Symplectic methods are implicit \(\Rightarrow\) problem for large systems
     
  • Semi-implicit methods tuned for spin-systems can be good trade-off

Slides available at: slides.com/kmodin