Who wants to use QBF solvers...

Without writing QBF?

Matthias van der Hallen (KU Leuven)

A higher level modelling language

Second Order (SO) Logic

A translator (grounder) to QBF

QBF

Modelling

language

Grounder

Goal

  • Make models shorter

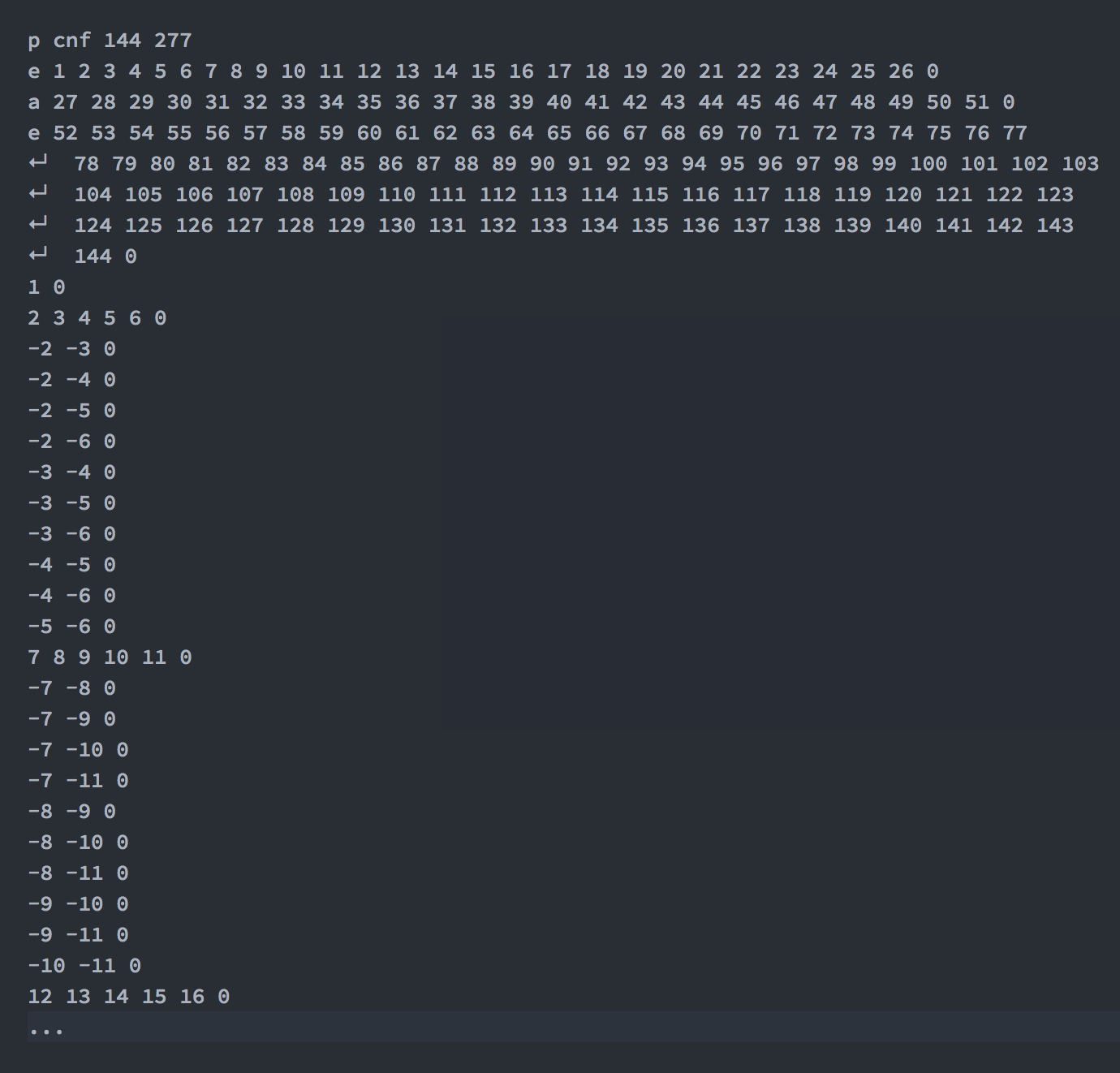
p cnf 144 277
e 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 0
a 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 0
e 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77	
⏎ 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102
⏎ 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123
⏎ 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 0
1 0
2 3 4 5 6 0
-2 -3 0
-2 -4 0
-2 -5 0
-2 -6 0
-3 -4 0
-3 -5 0
-3 -6 0
-4 -5 0
-4 -6 0
-5 -6 0
7 8 9 10 11 0
-7 -8 0
-7 -9 0
-7 -10 0
-7 -11 0
-8 -9 0
-8 -10 0
-8 -11 0
-9 -10 0
-9 -11 0
-10 -11 0
12 13 14 15 16 0
-12 -13 0
-12 -14 0
...

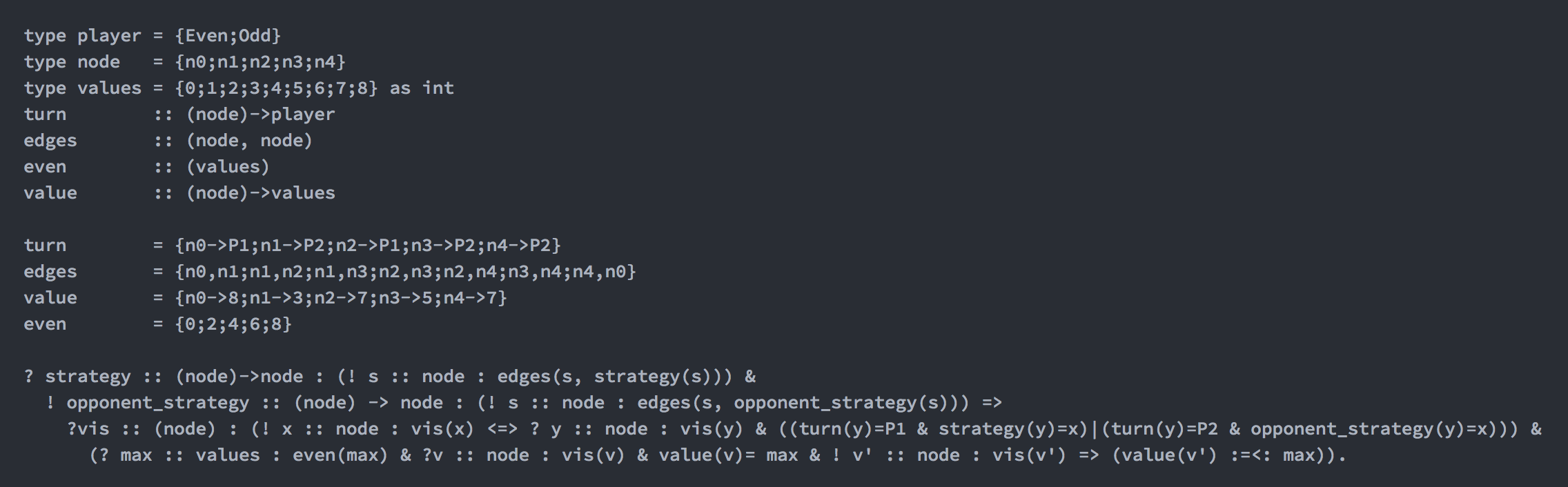
type player = {Even;Odd}
type node   = {n0;n1;n2;n3;n4}
type values = {0;1;2;3;4;5;6;7;8} as int
turn        :: (node)->player
edges       :: (node,node)
even        :: (values)
value       :: (node)->values

turn        = {n0->Even;n1->Odd;n2->Even;n3->Odd;n4->Odd}
edges       = {n0,n1;n1,n2;n1,n3;n2,n3;n2,n4;n3,n4;n4,n0}
value       = {n0->8;n1->3;n2->7;n3->5;n4->7}
even        = {0;2;4;6;8}

? strategy :: (node)->node : (! s :: node : edges(s,strategy(s))) &
  ! opponent_strategy :: (node) -> node : (! s :: node : edges(s,opponent_strategy(s))) =>
    ?vis :: (node) : (! x :: node : vis(x) <=> ? y :: node : vis(y) & ((turn(y)=Even & strategy(y)=x)|(turn(y)=Odd & opponent_strategy(y)=x))) &
      (? max :: values : even(max) & ?v :: node : vis(v) & value(v)= max & ! v' :: node : vis(v') => (value(v') :=<: max)).

Goal

  • Make models shorter

  • And better maintainable

  • Solver agnostic

    • Support QDIMACS
    • Support QCIR

In what modelling language could we write?

Logic!

Logic rules in Answer Set Programming

motive(harry).
motive(sally).
guilty(harry).

innocent(Suspect) :- motive(Suspect), not guilty(Suspect).

In what modelling language could we write?

First Order Logic in IDP

type Color
type Area
Border(Area,Area)
Coloring(Area):Color

∀a1[Area] ∀a2[Area] : Border(a1,a2) ∨ Border(a2,a1) ⇒ Coloring(a1) ≠ Coloring(a2).

In what modelling language could we write?

Neither Logic Rules or First Order Logic is expressive enough!

In what modelling language could we write?

A modelling language for QBF 

Second Order Logic

Second Order Logic

  • Domain elements and types

  • Predicates and functions

  • Formulas that quantify over variables:

    • Representing domain elements

    • Representing predicates/functions

\forall x \forall y \exists f . f(x)=y
∀x∀y∃f.f(x)=y\forall x \forall y \exists f . f(x)=y

Second Order Logic

Extensions:

  • Arithmetic: introduce subtypes of int

    • +, *, - and integer division

    • Comparisons <, >, =, ...

Second Order Logic

Under the hood

  • Unnest functions
  • Rewrite functions to predicates
  • Ground all FO quantifiers
    • Evaluate any arithmetic here

Second Order Logic

Under the hood

  • Unnest functions
  • Rewrite functions to predicates
  • Ground all FO quantifiers
  • For every predicate application \(p(x,y)\)
    • Introduce proposition \(p_{x,y}\)
    • Add it to quantifier prefix (at the right position)

Second Order Logic

Modelling:

  • Vocabulary:
    • Types
    • Top level, existentially quantified symbols

Second Order Logic

Modelling:

  • Vocabulary
  • Structure:
    • defining fully known symbols

Second Order Logic

Modelling:

  • Vocabulary
  • Structure
  • Theory:
    • Set of SO sentences

Examples

Strategic Companies

Set of companies and products

  • 'joint ownership' relation 

  • 'produces' relation

 

(QBFEVAL'06, '10, ...)

Strategic Companies

(QBFEVAL'06, '10, ...)

Strategic set:

  • producing all products

  • closed under ownership

minimal strategic sets

No subset forms its own strategic set

Strategic Companies

(QBFEVAL'06, '10, ...)

For companies \(c_1\), \(c_2\):

minimal strategic set containing \(c_1\), \(c_2\)?

Strategic Companies

Pasta

Tonno

Barilla

x

Dececco

x

Star

x

Callippo

X

Barilla

Dececco

Star

Is there a minimal strategic set containing:

Barilla and Star?

Barilla and Callipo?

owns

owns

Strategic Companies

Pasta

Tonno

Barilla

x

Dececco

x

Star

x

Callippo

X

Barilla

Dececco

Star

Minimal strategic sets:

Star, Barilla, and Dececco

Dececco and Callippo

owns

owns

a

b

c

d

e

f

g

h

Reachability

Can we reach \(b\) from \(a\)?

  • Boxes: Even player

  • Diamonds: Odd player

Parity Games

Is there a strategy for \(Even\) s.t. in every loop, the largest value is even?

Using a higher modelling language:

  • Shorter models

  • Easier to maintain

  • New encoding techniques / tricks for old models

(And I suggest Second Order Logic)

Benefits:

Using a higher modelling language:

Work in progress:

  • QCIR output

  • Do Not Repeat Yourself:

    • Higher order definitions

  • Aggregates

  • More informative output

    • proof generation / certificate extraction

Thank you

Made with Slides.com