Probabilistic Voting Model

Lecture 3, Political Economics I

OSIPP, Osaka University

27 October, 2017

Masa Kudamatsu

Did you come up with

a research question

for your term paper?

And is it

original, interesting, and feasible?

For your inspiration #1

Here's the list of policies my undergrad class students have chosen

to write their term paper on why they aren't adopted

For your inspiration #2

Taro Kono's blog (on his early days as a legislator)

For your inspiration #3

Political science books on why DPJ government failed

For your inspiration #4

Questions raised by the last general elections in Japan

Should Prime Minister be allowed to dissolve the parliament?

Do majoritarian elections really help opposition parties?

Why doesn't Japan introduce full proportional representation like in continental Europe?

For your inspiration #5

A Dutch designer proposes a new electoral rule

Instead of voting for one candidate / party,

vote by policy issue

His survey of 75,000 Dutch citizens shows

the correlation between their policy preferences

and the policies proposed by the party they vote

is only 10-20%

Motivations for today

Last week we saw how the citizen-candidate model

relaxes the commitment assumption

The Median Voter Theorem relies on restricting assumptions

This week we'll see how the probabilistic voting model

relaxes the assumption on voters' preference

Single-peaked / Single-crossing for one-dimensional policy

Intermediate preference for multi-dimensional policy

Example: Distribution of Local Public Goods

Demography

Endowment

\(N\) citizens live in several districts, each indexed by \(J\)

Population of district \(J\): \(N^J\)

(\(\sum_J N^J = N\))

Every citizen earns exogenous income \(y\)

(for simplicity)

Example: Distribution of Local Public Goods

Preference of each citizen in district \(J\) 

c^J + H(g^J)
cJ+H(gJ)c^J + H(g^J)

Private

consumption

Local

public goods

per capita

where \(H(\cdot)\) is increasing and concave, with \(H(0)=0\)

Government

collects lump sum tax \(\tau\) from every citizen

Government budget constraint

provides per capita local public goods to each district, \(g^J\)

\sum_J N^J g^J = N\tau
∑JNJgJ=Nτ\sum_J N^J g^J = N\tau

Example: Distribution of Local Public Goods (cont.)

District \(J\) citizens' preference over policies

(\Leftarrow \sum_I N^I g^I = N\tau)
(⇐∑INIgI=Nτ)(\Leftarrow \sum_I N^I g^I = N\tau)
W^J(\mathbf{g})=y-\tau+H(g^J)
WJ(g)=y−τ+H(gJ)W^J(\mathbf{g})=y-\tau+H(g^J)
(\Leftarrow c^J = y - \tau)
(⇐cJ=y−τ)(\Leftarrow c^J = y - \tau)
=y-\sum_I\frac{N^I}{N}g^I +H(g^J)
=y−∑ININgI+H(gJ)=y-\sum_I\frac{N^I}{N}g^I +H(g^J)

Example: Distribution of Local Public Goods (cont.)

District \(J\) citizens' preference over policies

W^J(\mathbf{g})=y-\sum_I\frac{N^I}{N}g^I +H(g^J)
WJ(g)=y−∑ININgI+H(gJ)W^J(\mathbf{g})=y-\sum_I\frac{N^I}{N}g^I +H(g^J)

Their ideal policy is given by

H_g(g^J)=1
Hg(gJ)=1H_g(g^J)=1
g^I=0, \forall I \neq J
gI=0,∀I≠Jg^I=0, \forall I \neq J

No "median" policy exists: no equilibrium in Downsian model

Example: Distribution of Local Public Goods (cont.)

g^J
gJg^J
H_g(g^J)
Hg(gJ)H_g(g^J)
1
11

Example: Distribution of Local Public Goods (cont.)

Probabilistic voting model does have an equilibrium

as long as citizens' policy preference is continuous and concave

District \(J\) citizens' preference over policies

W^J(\mathbf{g})=y-\sum_I\frac{N^I}{N}g^I +H(g^J)
WJ(g)=y−∑ININgI+H(gJ)W^J(\mathbf{g})=y-\sum_I\frac{N^I}{N}g^I +H(g^J)

For the purpose of understanding distortion by politics,

derive the first-best policy:

\max_{\mathbf{g}}\sum_JN^J(c^J+H(g^J))
maxg∑JNJ(cJ+H(gJ))\max_{\mathbf{g}}\sum_JN^J(c^J+H(g^J))
\text{s.t.} \sum_JN^J(g^J+c^J)=Ny
s.t.∑JNJ(gJ+cJ)=Ny\text{s.t.} \sum_JN^J(g^J+c^J)=Ny

Sum of utilities

Resource constraint

\max_{\mathbf{g}}[Ny-\sum_JN^Jg^J]+\sum_JN^JH(g^J)
maxg[Ny−∑JNJgJ]+∑JNJH(gJ)\max_{\mathbf{g}}[Ny-\sum_JN^Jg^J]+\sum_JN^JH(g^J)
H_g(g^{J,FB})=1, \forall J
Hg(gJ,FB)=1,∀JH_g(g^{J,FB})=1, \forall J

Example: Distribution of Local Public Goods (cont.)

First-best given by: 

Basic Model

We follow Sections 3.4 & 7.4 of Persson and Tabellini (2000)

Originally proposed by Lindbeck and Weibull (1987)

Players

Each belongs to a group indexed by \(J\)

Two candidates, \(A, B\)

Denote the population share of group \(J\) by \(\alpha^J\)

(\sum_J \alpha^J = 1)
(∑JαJ=1)(\sum_J \alpha^J = 1)

\(N\) citizens, each indexed by \(i\)

Candidates' preference and action

We assume they can commit to this policy

Each candidate's payoff is given by:

Before the election, each announces the policy vector \(\mathbf{q}_A, \mathbf{q}_B\)

Note: we no longer need to stick to one-dimensional policy

So we assume office-seeking politicians

\(R\)   if elected (ego-rent)

\(0\)   otherwise (normalization)

A way to get round the commitment assumption

Assume there are two political parties, A and B

Each party selects a candidate based on their ideal policy 

Remaining issue:

Does the party stick to its candidate after winning the election?

Yes in the U.S.

No in Japan: the ruling party often replaces its leader (ie. Prime Minister) between elections

Citizens' preference

Citizens care about (1) policies and (2) who wins

Citizens' preference

Citizens care about (1) policies and (2) who wins

where \(P\) denotes the winning candidate

Note:

All citizens in the same group have the same preference on policies

W^J(\mathbf{q}_P)
WJ(qP)W^J(\mathbf{q}_P)

\(W^J(\cdot)\) is a continuous and concave function

\(W^J(\cdot)\) doesn't have to be single-peaked, single-crossing, or intermediate

Citizens' preference

Citizens care about (1) policies and (2) who wins

where \(D_B\) is 1 if B wins and 0 otherwise

Individual ideological bias

\sigma^{iJ}
σiJ\sigma^{iJ}

Population-wide popularity for candidate B

\delta
δ\delta

These two parameters are unknown to candidates

W^J(\mathbf{q}_P)
WJ(qP)W^J(\mathbf{q}_P)
+ D_B(\sigma^{iJ}+\delta)
+DB(σiJ+δ)+ D_B(\sigma^{iJ}+\delta)

Information

Candidates face uncertainty about citizens' preference

W^J(\mathbf{q}_P)
WJ(qP)W^J(\mathbf{q}_P)
+ D_B(\sigma^{iJ}+\delta)
+DB(σiJ+δ)+ D_B(\sigma^{iJ}+\delta)

Known

Unknown

But candidates know the distribution of the unknown parameters

Information (cont.)

Assume the following distributions for population-wide shock:

\big[-\frac{1}{2\psi}, \frac{1}{2\psi}\big]
[−12ψ,12ψ]\big[-\frac{1}{2\psi}, \frac{1}{2\psi}\big]

uniformly distributed over

\delta
δ\delta

Density

\psi
ψ\psi
-\frac{1}{2\psi}
−12ψ-\frac{1}{2\psi}
\frac{1}{2\psi}
12ψ\frac{1}{2\psi}
0
00
\delta
δ\delta

To allow explicit solutions...

Information (cont.)

uniformly distributed over

\sigma^{iJ}
σiJ\sigma^{iJ}

Assume the following distributions for individual bias for B:

\big[-\frac{1}{2\phi^J}, \frac{1}{2\phi^J}\big]
[−12ϕJ,12ϕJ]\big[-\frac{1}{2\phi^J}, \frac{1}{2\phi^J}\big]
\sigma^{iJ}
σiJ\sigma^{iJ}

Density

\phi^J
ϕJ\phi^J
-\frac{1}{2\phi^J}
−12ϕJ-\frac{1}{2\phi^J}
\frac{1}{2\phi^J}
12ϕJ\frac{1}{2\phi^J}
0
00

Biased for B

Biased for A

To allow explicit solutions...

Information (cont.)

uniformly distributed over

\sigma^{iJ}
σiJ\sigma^{iJ}
\big[-\frac{1}{2\phi^J}, \frac{1}{2\phi^J}\big]
[−12ϕJ,12ϕJ]\big[-\frac{1}{2\phi^J}, \frac{1}{2\phi^J}\big]
\sigma^{iJ}
σiJ\sigma^{iJ}

Density

\phi^J
ϕJ\phi^J
-\frac{1}{2\phi^J}
−12ϕJ-\frac{1}{2\phi^J}
\frac{1}{2\phi^J}
12ϕJ\frac{1}{2\phi^J}
0
00

For higher \(\phi^J\)

Assume the following distributions for individual bias for B:

To allow explicit solutions...

measures how homogenous group J is

\phi^J
ϕJ\phi^J

Information (cont.)

These distributions can be generalized

as long as its unimodal and symmetric around the mean

e.g. Normal distribution

Timing of Events

1

2

3

4

Candidates A and B simultaneously announce

their policy platform

\mathbf{q}_A, \mathbf{q}_B
qA,qB\mathbf{q}_A, \mathbf{q}_B

Nature picks individual ideological bias \(\sigma^{iJ}\) and aggregate popularity shocks \(\delta\)  for B

Citizens decide which candidate to vote for

The winning candidate implements the announced policy

Analysis

Backward induction

1

2

3

4

Candidates A and B simultaneously announce

their policy platform

Popularity shocks for B, both individual (\(\sigma^{iJ}\)) and aggregate (\(\delta\)), realize

Citizens decide which candidate to vote for

The winning candidate implements the announced policy

\mathbf{q}_A, \mathbf{q}_B
qA,qB\mathbf{q}_A, \mathbf{q}_B

Citizens' optimization

Citizen i of group J votes for A if

W^J(\mathbf{q}_A)>W^J(\mathbf{q}_B)+\sigma^{iJ}+\delta
WJ(qA)>WJ(qB)+σiJ+δW^J(\mathbf{q}_A)>W^J(\mathbf{q}_B)+\sigma^{iJ}+\delta
\sigma^{iJ}<\sigma^J \equiv W^J(\mathbf{q}_A) - W^J(\mathbf{q}_B)-\delta
σiJ<σJ≡WJ(qA)−WJ(qB)−δ\sigma^{iJ}<\sigma^J \equiv W^J(\mathbf{q}_A) - W^J(\mathbf{q}_B)-\delta

or

\sigma^{iJ}
σiJ\sigma^{iJ}

Density

\phi^J
ϕJ\phi^J
-\frac{1}{2\phi^J}
−12ϕJ-\frac{1}{2\phi^J}
\frac{1}{2\phi^J}
12ϕJ\frac{1}{2\phi^J}
\sigma^J
σJ\sigma^J

Vote for B

Vote for A

\sigma^J \equiv W^J(\mathbf{q}_A) - W^J(\mathbf{q}_B)-\delta
σJ≡WJ(qA)−WJ(qB)−δ\sigma^J \equiv W^J(\mathbf{q}_A) - W^J(\mathbf{q}_B)-\delta

Citizens' optimization (cont.)

Backward induction

1

2

3

4

Candidates A and B simultaneously announce

their policy platform

Popularity shocks for B, both individual (\(\sigma^{iJ}\)) and aggregate (\(\delta\)), realize

Citizens decide which candidate to vote for

The winning candidate implements the announced policy

\mathbf{q}_A, \mathbf{q}_B
qA,qB\mathbf{q}_A, \mathbf{q}_B

Candidate A's optimization

\max_{\mathbf{q}_A}p_AR + (1-p_A)*0
maxqApAR+(1−pA)∗0\max_{\mathbf{q}_A}p_AR + (1-p_A)*0

where the winning probability is given by

p_A=\Pr(\pi_A\geq \frac{1}{2})
pA=Pr(πA≥12)p_A=\Pr(\pi_A\geq \frac{1}{2})

A's vote share

How does \(\pi_A\) depend on \(\mathbf{q}_A\)?

\sigma^{iJ}
σiJ\sigma^{iJ}

Density

\phi^J
ϕJ\phi^J
-\frac{1}{2\phi^J}
−12ϕJ-\frac{1}{2\phi^J}
\frac{1}{2\phi^J}
12ϕJ\frac{1}{2\phi^J}
\sigma^J
σJ\sigma^J

Vote for B

Vote for A

Thus A's vote share among group J citizens is given by

\pi^J_A=\phi^J(\sigma^J-(-\frac{1}{2\phi^J}))
πAJ=ϕJ(σJ−(−12ϕJ))\pi^J_A=\phi^J(\sigma^J-(-\frac{1}{2\phi^J}))

Candidate A's vote share among group J citizens

= \phi^J\sigma^J+\frac{1}{2}
=ϕJσJ+12 = \phi^J\sigma^J+\frac{1}{2}

Candidate A's vote share among all citizens

\pi_A=\sum_J \alpha^J\pi^J_A
πA=∑JαJπAJ\pi_A=\sum_J \alpha^J\pi^J_A
=\sum_J \alpha^J(\phi^J\sigma^J+\frac{1}{2})
=∑JαJ(ϕJσJ+12)=\sum_J \alpha^J(\phi^J\sigma^J+\frac{1}{2})

(Remember \(\alpha^J\) denotes group J's population share)

where

\sigma^J \equiv W^J(\mathbf{q}_A) - W^J(\mathbf{q}_B) -\delta
σJ≡WJ(qA)−WJ(qB)−δ\sigma^J \equiv W^J(\mathbf{q}_A) - W^J(\mathbf{q}_B) -\delta

Unlike in the Downsian model,

here the vote share is a continuous function of policies

thanks to stochastic \(\sigma^{iJ}\)

=\frac{1}{2}+\sum_J \alpha^J\phi^J\sigma^J
=12+∑JαJϕJσJ=\frac{1}{2}+\sum_J \alpha^J\phi^J\sigma^J

Candidate A's vote share among all citizens

\pi_A=\sum_J \alpha^J\pi^J_A
πA=∑JαJπAJ\pi_A=\sum_J \alpha^J\pi^J_A

where

\sigma^J \equiv W^J(\mathbf{q}_A) - W^J(\mathbf{q}_B) -\delta
σJ≡WJ(qA)−WJ(qB)−δ\sigma^J \equiv W^J(\mathbf{q}_A) - W^J(\mathbf{q}_B) -\delta

But candidates maximize the winning probability, not the vote share

If \(\delta\) is known, \(\Pr(\pi_A\geq 1/2)\) is not continuous w.r.t. \(\mathbf{q}_A\) 

=\frac{1}{2}+\sum_J \alpha^J\phi^J\sigma^J
=12+∑JαJϕJσJ=\frac{1}{2}+\sum_J \alpha^J\phi^J\sigma^J

Candidate A's vote share among all citizens

\pi_A=\sum_J \alpha^J\pi^J_A
πA=∑JαJπAJ\pi_A=\sum_J \alpha^J\pi^J_A

where

\sigma^J \equiv W^J(\mathbf{q}_A) - W^J(\mathbf{q}_B) -\delta
σJ≡WJ(qA)−WJ(qB)−δ\sigma^J \equiv W^J(\mathbf{q}_A) - W^J(\mathbf{q}_B) -\delta

Random variable when candidates choose their policy

Make the winning probability a continuous function of policies

=\frac{1}{2}+\sum_J \alpha^J\phi^J\sigma^J
=12+∑JαJϕJσJ=\frac{1}{2}+\sum_J \alpha^J\phi^J\sigma^J

Candidate A's winning probability

Rearranging terms...

=\frac{1}{2}+\sum_J\alpha^J\phi^J(W^J(g_A)-W^J(g_B)-\delta)
=12+∑JαJϕJ(WJ(gA)−WJ(gB)−δ)=\frac{1}{2}+\sum_J\alpha^J\phi^J(W^J(g_A)-W^J(g_B)-\delta)
=\frac{1}{2}+\sum_J\alpha^J\phi^J(W^J(g_A)-W^J(g_B))
=12+∑JαJϕJ(WJ(gA)−WJ(gB))=\frac{1}{2}+\sum_J\alpha^J\phi^J(W^J(g_A)-W^J(g_B))

Now we want to know the probability that \(\pi_A\geq1/2\)

\pi_A=\frac{1}{2}+\sum_J \alpha^J\phi^J\sigma^J
πA=12+∑JαJϕJσJ\pi_A=\frac{1}{2}+\sum_J \alpha^J\phi^J\sigma^J
-\delta\sum_J\alpha^J\phi^J
−δ∑JαJϕJ-\delta\sum_J\alpha^J\phi^J

Candidate A's winning probability

Rearranging terms...

=\frac{1}{2}+\sum_J\alpha^J\phi^J(W^J(g_A)-W^J(g_B)-\delta)
=12+∑JαJϕJ(WJ(gA)−WJ(gB)−δ)=\frac{1}{2}+\sum_J\alpha^J\phi^J(W^J(g_A)-W^J(g_B)-\delta)
=\frac{1}{2}+\sum_J\alpha^J\phi^J(W^J(g_A)-W^J(g_B))
=12+∑JαJϕJ(WJ(gA)−WJ(gB))=\frac{1}{2}+\sum_J\alpha^J\phi^J(W^J(g_A)-W^J(g_B))
-\delta\sum_J\alpha^J\phi^J
−δ∑JαJϕJ-\delta\sum_J\alpha^J\phi^J
\pi_A=\frac{1}{2}+\sum_J \alpha^J\phi^J\sigma^J
πA=12+∑JαJϕJσJ\pi_A=\frac{1}{2}+\sum_J \alpha^J\phi^J\sigma^J

That is, the probability that these terms are larger than zero

Candidate A's winning probability

\sum_J\alpha^J\phi^J(W^J(g_A)-W^J(g_B))
∑JαJϕJ(WJ(gA)−WJ(gB))\sum_J\alpha^J\phi^J(W^J(g_A)-W^J(g_B))
\geq\delta\sum_J\alpha^J\phi^J
≥δ∑JαJϕJ\geq\delta\sum_J\alpha^J\phi^J

That is, the probability that this inequality holds

Candidate A wins if 

\pi_A\geq \frac{1}{2}
πA≥12\pi_A\geq \frac{1}{2}

or

\sum_J\alpha^J\phi^J(W^J(g_A)-W^J(g_B))\geq \delta\sum_J\alpha^J\phi^J
∑JαJϕJ(WJ(gA)−WJ(gB))≥δ∑JαJϕJ\sum_J\alpha^J\phi^J(W^J(g_A)-W^J(g_B))\geq \delta\sum_J\alpha^J\phi^J

or

\delta \leq \frac{1}{\phi}\sum_J\alpha^J\phi^J(W^J(g_A)-W^J(g_B))
δ≤1ϕ∑JαJϕJ(WJ(gA)−WJ(gB))\delta \leq \frac{1}{\phi}\sum_J\alpha^J\phi^J(W^J(g_A)-W^J(g_B))

where

\phi\equiv\sum_J\alpha^J\phi^J
ϕ≡∑JαJϕJ\phi\equiv\sum_J\alpha^J\phi^J

(average homogeneity)

Candidate A's winning probability (cont.)

Candidate A's winning probability

Candidate A wins if 

Now since 

\delta
δ\delta

is uniformly distributed within

\big[-\frac{1}{2\psi}, \frac{1}{2\psi}\big]
[−12ψ,12ψ]\big[-\frac{1}{2\psi}, \frac{1}{2\psi}\big]

we can obtain the probability that 

\pi_A\geq \frac{1}{2}
πA≥12\pi_A\geq \frac{1}{2}
\delta \leq \frac{1}{\phi}\sum_J\alpha^J\phi^J(W^J(g_A)-W^J(g_B))
δ≤1ϕ∑JαJϕJ(WJ(gA)−WJ(gB))\delta \leq \frac{1}{\phi}\sum_J\alpha^J\phi^J(W^J(g_A)-W^J(g_B))
\Pr[\delta \leq \frac{1}{\phi}\sum_J\alpha^J\phi^J(W^J(\mathbf{q}_A)-W^J(\mathbf{q}_B))]
Pr[δ≤1ϕ∑JαJϕJ(WJ(qA)−WJ(qB))]\Pr[\delta \leq \frac{1}{\phi}\sum_J\alpha^J\phi^J(W^J(\mathbf{q}_A)-W^J(\mathbf{q}_B))]
\delta
δ\delta

Density

\psi
ψ\psi
-\frac{1}{2\psi}
−12ψ-\frac{1}{2\psi}
\frac{1}{2\psi}
12ψ\frac{1}{2\psi}
\frac{1}{\phi}\sum_J\alpha^J\phi^J(W^J(\mathbf{q}_A)-W^J(\mathbf{q}_B))
1ϕ∑JαJϕJ(WJ(qA)−WJ(qB))\frac{1}{\phi}\sum_J\alpha^J\phi^J(W^J(\mathbf{q}_A)-W^J(\mathbf{q}_B))

A wins

=\psi[ \frac{1}{\phi}\sum_J\alpha^J\phi^J(W^J(\mathbf{q}_A)-W^J(\mathbf{q}_B))-(-\frac{1}{2\psi})]
=ψ[1ϕ∑JαJϕJ(WJ(qA)−WJ(qB))−(−12ψ)]=\psi[ \frac{1}{\phi}\sum_J\alpha^J\phi^J(W^J(\mathbf{q}_A)-W^J(\mathbf{q}_B))-(-\frac{1}{2\psi})]

Candidate A's winning probability (cont.)

=\frac{1}{2}+\frac{\psi}{\phi}\sum_J\alpha^J\phi^J(W^J(\mathbf{q}_A)-W^J(\mathbf{q}_B))
=12+ψϕ∑JαJϕJ(WJ(qA)−WJ(qB))=\frac{1}{2}+\frac{\psi}{\phi}\sum_J\alpha^J\phi^J(W^J(\mathbf{q}_A)-W^J(\mathbf{q}_B))

Candidate A's winning probability (cont.)

\Pr[\delta \leq \frac{1}{\phi}\sum_J\alpha^J\phi^J(W^J(\mathbf{q}_A)-W^J(\mathbf{q}_B))]
Pr[δ≤1ϕ∑JαJϕJ(WJ(qA)−WJ(qB))]\Pr[\delta \leq \frac{1}{\phi}\sum_J\alpha^J\phi^J(W^J(\mathbf{q}_A)-W^J(\mathbf{q}_B))]
=\psi[ \frac{1}{\phi}\sum_J\alpha^J\phi^J(W^J(\mathbf{q}_A)-W^J(\mathbf{q}_B))-(-\frac{1}{2\psi})]
=ψ[1ϕ∑JαJϕJ(WJ(qA)−WJ(qB))−(−12ψ)]=\psi[ \frac{1}{\phi}\sum_J\alpha^J\phi^J(W^J(\mathbf{q}_A)-W^J(\mathbf{q}_B))-(-\frac{1}{2\psi})]

Note: The winning probability is a continuous function of the policy

cf. This is not the case for the Downsian model

\Pr[\pi_B\geq\frac{1}{2}] = (1-\Pr[\pi_A\geq\frac{1}{2}])
Pr[πB≥12]=(1−Pr[πA≥12])\Pr[\pi_B\geq\frac{1}{2}] = (1-\Pr[\pi_A\geq\frac{1}{2}])
=\frac{1}{2}+\frac{\psi}{\phi}\sum_J\alpha^J\phi^J(W^J(\mathbf{q}_B)-W^J(\mathbf{q}_A))
=12+ψϕ∑JαJϕJ(WJ(qB)−WJ(qA))=\frac{1}{2}+\frac{\psi}{\phi}\sum_J\alpha^J\phi^J(W^J(\mathbf{q}_B)-W^J(\mathbf{q}_A))
\Pr[\pi_A\geq\frac{1}{2}]=\frac{1}{2}+\frac{\psi}{\phi}\sum_J\alpha^J\phi^J(W^J(\mathbf{q}_A)-W^J(\mathbf{q}_B))
Pr[πA≥12]=12+ψϕ∑JαJϕJ(WJ(qA)−WJ(qB))\Pr[\pi_A\geq\frac{1}{2}]=\frac{1}{2}+\frac{\psi}{\phi}\sum_J\alpha^J\phi^J(W^J(\mathbf{q}_A)-W^J(\mathbf{q}_B))

Candidate A's winning probability

Candidate B's winning probability

Both candidates' objective is

concave in their own action (i.e. policy)

continuous in the other candidate's action

A Nash equilibrium exists

(see e.g. Section 1.3.3 of Fudenberg and Tirole 1991)

\Pr[\pi_B\geq\frac{1}{2}] = (1-\Pr[\pi_A\geq\frac{1}{2}])
Pr[πB≥12]=(1−Pr[πA≥12])\Pr[\pi_B\geq\frac{1}{2}] = (1-\Pr[\pi_A\geq\frac{1}{2}])

Both candidates solve the same maximization problem

In the equilibrium, both candidates propose the same policy

\Pr[\pi_A\geq\frac{1}{2}]=\frac{1}{2}+\frac{\psi}{\phi}\sum_J\alpha^J\phi^J(W^J(\mathbf{q}_A)-W^J(\mathbf{q}_B))
Pr[πA≥12]=12+ψϕ∑JαJϕJ(WJ(qA)−WJ(qB))\Pr[\pi_A\geq\frac{1}{2}]=\frac{1}{2}+\frac{\psi}{\phi}\sum_J\alpha^J\phi^J(W^J(\mathbf{q}_A)-W^J(\mathbf{q}_B))

Candidate A's winning probability

Candidate B's winning probability

=\frac{1}{2}+\frac{\psi}{\phi}\sum_J\alpha^J\phi^J(W^J(\mathbf{q}_B)-W^J(\mathbf{q}_A))
=12+ψϕ∑JαJϕJ(WJ(qB)−WJ(qA))=\frac{1}{2}+\frac{\psi}{\phi}\sum_J\alpha^J\phi^J(W^J(\mathbf{q}_B)-W^J(\mathbf{q}_A))
W^J(\mathbf{q}_A)=W^J(\mathbf{q}_B)
WJ(qA)=WJ(qB)W^J(\mathbf{q}_A)=W^J(\mathbf{q}_B)
\sigma^{iJ}
σiJ\sigma^{iJ}

Density

\phi^J
ϕJ\phi^J
-\frac{1}{2\phi^J}
−12ϕJ-\frac{1}{2\phi^J}
\frac{1}{2\phi^J}
12ϕJ\frac{1}{2\phi^J}
\sigma^J
σJ\sigma^J

Vote for B

Vote for A

\sigma^J \equiv W^J(\mathbf{q}_A) - W^J(\mathbf{q}_B)-\delta
σJ≡WJ(qA)−WJ(qB)−δ\sigma^J \equiv W^J(\mathbf{q}_A) - W^J(\mathbf{q}_B)-\delta

In the equilibrium...

=-\delta
=−δ=-\delta

Implications

Implications from Probabilistic Voting Model

1

Equilibrium policies

maximize the weighted sum of citizens' payoffs

2

Politicians target swing voters, not loyal voters

3

Median voters are not necessarily decisive

Equilibrium policy maximizes a weighted sum of citizen payoffs

\Pr[\pi_A\geq\frac{1}{2}]
Pr[πA≥12]\Pr[\pi_A\geq\frac{1}{2}]
=\frac{1}{2}+\frac{\psi}{\phi}\sum_J\alpha^J\phi^J(W^J(g_A)-W^J(g_B))
=12+ψϕ∑JαJϕJ(WJ(gA)−WJ(gB))=\frac{1}{2}+\frac{\psi}{\phi}\sum_J\alpha^J\phi^J(W^J(g_A)-W^J(g_B))

More populous or more homogenous groups

are treated better

Macroeconomists often use this result to endogenize policies

e.g. Song et al. (2012 Econometrica) on government debt

Implication 1

Each candidate maximizes the winning probability given by

Group J's weight: \(\alpha^J \phi^J\)

Implication 2: Swing Voter Hypothesis

Swing voters: those not loyal to any candidate/party (無党派層)

In the model, those groups with high \(\phi^J\)

\sigma^{iJ}
σiJ\sigma^{iJ}
\phi^J
ϕJ\phi^J
0
00

Implication 2: Swing Voter Hypothesis

Swing voters: those not loyal to any candidate/party (無党派層)

The model predicts

politicians mostly please those groups with high \(\phi^J\)

\sigma^{iJ}
σiJ\sigma^{iJ}
\phi^J
ϕJ\phi^J
0
00

We now illustrate the swing voter hypothesis

in the example of distribution of local public goods

that we saw at the beginning of this lecture

See Section 7.4 of Persson and Tabellini (2000) for detail

District \(J\) citizens' preference over policies

W^J(\mathbf{g})=y-\sum_I\frac{N^I}{N}g^I +H(g^J)
WJ(g)=y−∑ININgI+H(gJ)W^J(\mathbf{g})=y-\sum_I\frac{N^I}{N}g^I +H(g^J)

Example: Distribution of Local Public Goods (revisited)

g^J
gJg^J
H_g(g^J)
Hg(gJ)H_g(g^J)
1
11

First-best policies:

H_g(g^J)=1, \forall J
Hg(gJ)=1,∀JH_g(g^J)=1, \forall J

Distribution of Local Public Goods

Candidate's problem

\max_{\mathbf{g}_A}p_AR
maxgApAR\max_{\mathbf{g}_A}p_AR
p_A=\frac{1}{2}+\frac{\psi}{\phi}\sum_J\alpha^J\phi^J(W^J(\mathbf{g}_A)-W^J(\mathbf{g}_B))
pA=12+ψϕ∑JαJϕJ(WJ(gA)−WJ(gB))p_A=\frac{1}{2}+\frac{\psi}{\phi}\sum_J\alpha^J\phi^J(W^J(\mathbf{g}_A)-W^J(\mathbf{g}_B))

where

\alpha^J=\frac{N^J}{N}
αJ=NJN\alpha^J=\frac{N^J}{N}

That is, 

\max_{\mathbf{g}_A}\frac{\psi}{\phi}\sum_J\alpha^J\phi^JW^J(\mathbf{g}_A)
maxgAψϕ∑JαJϕJWJ(gA)\max_{\mathbf{g}_A}\frac{\psi}{\phi}\sum_J\alpha^J\phi^JW^J(\mathbf{g}_A)

where

W^J(\mathbf{g}_A)=y-\sum_I\alpha^Ig_A^I +H(g_A^J)
WJ(gA)=y−∑IαIgAI+H(gAJ)W^J(\mathbf{g}_A)=y-\sum_I\alpha^Ig_A^I +H(g_A^J)

Distribution of Local Public Goods (cont.)

Candidate's problem

\max_{\mathbf{g}_A}\frac{\psi}{\phi}\sum_J\alpha^J\phi^J[y-\sum_I\alpha^Ig_A^I +H(g_A^J)]
maxgAψϕ∑JαJϕJ[y−∑IαIgAI+H(gAJ)]\max_{\mathbf{g}_A}\frac{\psi}{\phi}\sum_J\alpha^J\phi^J[y-\sum_I\alpha^Ig_A^I +H(g_A^J)]

Distribution of Local Public Goods (cont.)

FOC w.r.t. \(g^J_A\)

\alpha^J\phi^J[H_g(g_A^J)-\alpha^J]=\alpha^J\sum_{I\neq J}\alpha^I\phi^I
αJϕJ[Hg(gAJ)−αJ]=αJ∑I≠JαIϕI\alpha^J\phi^J[H_g(g_A^J)-\alpha^J]=\alpha^J\sum_{I\neq J}\alpha^I\phi^I

Candidate's problem

\max_{\mathbf{g}_A}\frac{\psi}{\phi}\sum_J\alpha^J\phi^J[y-\sum_I\alpha^Ig_A^I +H(g_A^J)]
maxgAψϕ∑JαJϕJ[y−∑IαIgAI+H(gAJ)]\max_{\mathbf{g}_A}\frac{\psi}{\phi}\sum_J\alpha^J\phi^J[y-\sum_I\alpha^Ig_A^I +H(g_A^J)]
\phi^JH_g(g_A^J) =\sum_{I}\alpha^I\phi^I
ϕJHg(gAJ)=∑IαIϕI\phi^JH_g(g_A^J) =\sum_{I}\alpha^I\phi^I
H_g(g_A^J)=\frac{\sum_I\alpha^I\phi^I}{\phi^J}
Hg(gAJ)=∑IαIϕIϕJH_g(g_A^J)=\frac{\sum_I\alpha^I\phi^I}{\phi^J}

Or

Or

Distribution of Local Public Goods (cont.)

FOC w.r.t. \(g^J_A\)

\sigma^{iJ}
σiJ\sigma^{iJ}
\phi^J
ϕJ\phi^J
H_g(g_A^J)-\alpha^J
Hg(gAJ)−αJH_g(g_A^J)-\alpha^J

Switch to vote for A

For district \(J\)

\alpha^J\phi^J[H_g(g_A^J)-\alpha^J]=\alpha^J\sum_{I\neq J}\alpha^I\phi^I
αJϕJ[Hg(gAJ)−αJ]=αJ∑I≠JαIϕI\alpha^J\phi^J[H_g(g_A^J)-\alpha^J]=\alpha^J\sum_{I\neq J}\alpha^I\phi^I

The gain of voters in district \(J\)

Distribution of Local Public Goods (cont.)

FOC w.r.t. \(g^J_A\)

\sigma^{iJ}
σiJ\sigma^{iJ}
\phi^J
ϕJ\phi^J
\alpha^J
αJ\alpha^J

Switch to vote for B

For districts \(I\neq J\)

\alpha^J\phi^J[H_g(g_A^J)-\alpha^J]=\alpha^J\sum_{I\neq J}\alpha^I\phi^I
αJϕJ[Hg(gAJ)−αJ]=αJ∑I≠JαIϕI\alpha^J\phi^J[H_g(g_A^J)-\alpha^J]=\alpha^J\sum_{I\neq J}\alpha^I\phi^I

The loss of voters in districts \(I\neq J\)

Distribution of Local Public Goods (cont.)

FOC w.r.t. \(g^J_A\)

\phi^JH_g(g_A^J) =\sum_{I}\alpha^I\phi^I
ϕJHg(gAJ)=∑IαIϕI\phi^JH_g(g_A^J) =\sum_{I}\alpha^I\phi^I
H_g(g_A^J)=\frac{\sum_I\alpha^I\phi^I}{\phi^J}
Hg(gAJ)=∑IαIϕIϕJH_g(g_A^J)=\frac{\sum_I\alpha^I\phi^I}{\phi^J}

Or

Or

\alpha^J\phi^J[H_g(g_A^J)-\alpha^J]=\alpha^J\sum_{I\neq J}\alpha^I\phi^I
αJϕJ[Hg(gAJ)−αJ]=αJ∑I≠JαIϕI\alpha^J\phi^J[H_g(g_A^J)-\alpha^J]=\alpha^J\sum_{I\neq J}\alpha^I\phi^I

Distribution of Local Public Goods

FOC w.r.t. \(g^J_A\)

H_g(g_A^J)=\frac{\sum_I\alpha^I\phi^I}{\phi^J}
Hg(gAJ)=∑IαIϕIϕJH_g(g_A^J)=\frac{\sum_I\alpha^I\phi^I}{\phi^J}

For groups with \(\phi^J\) higher than the average (\(\sum_I\alpha^I\phi^I\))

H_g(g_A^{J*})=\frac{\sum_I\alpha^I\phi^I}{\phi^J}<1 = H_g(g^{J,FB})
Hg(gAJ∗)=∑IαIϕIϕJ<1=Hg(gJ,FB)H_g(g_A^{J*})=\frac{\sum_I\alpha^I\phi^I}{\phi^J}<1 = H_g(g^{J,FB})

i.e. Politically more responsive voter groups

      receive more than socially optimal

Swing Voter Hypothesis

More generally speaking, politicians target voter groups like

\sigma^{iJ}
σiJ\sigma^{iJ}
\phi^J
ϕJ\phi^J

0

instead of targeting voter groups like

\sigma^{iJ}
σiJ\sigma^{iJ}
\phi^J
ϕJ\phi^J

0

See Proposition 1 of Casey (2015) for the formal argument on this

Swing Voter Hypothesis

More generally speaking, politicians target voter groups like

\sigma^{iJ}
σiJ\sigma^{iJ}
\phi^J
ϕJ\phi^J

0

instead of targeting voter groups like

\sigma^{iJ}
σiJ\sigma^{iJ}
\phi^J
ϕJ\phi^J

0

We'll see evidence for this hypothesis shortly

Implication 3:

Median voters are not necessarily decisive

See Section 3.4 of Persson and Tabellini (2000) for detail

We illustrate this with a policy example (size of government)

from Lecture 1

Size of government

Preference of citizens in group \(J\)

(1-\tau)y^J+H(g)
(1−τ)yJ+H(g)(1-\tau)y^J+H(g)

Three groups of citizens \(J \in {P, M, R} \)

Group \(J\) citizens earn an exogenous income \( y^J \) with

y^P < y^M < y^R
yP<yM<yRy^P < y^M < y^R

Each group's population share (\(\alpha^J\)) is less than 1/2

Demography

Endowment

Population is normalized to be 1

Size of government

Government budget constraint

\sum_J \alpha^J\tau y^J=g
∑JαJτyJ=g\sum_J \alpha^J\tau y^J=g

Citizen's preference over policy

W^J(g)=(1-\frac{g}{\sum_J\alpha^Jy^J})y^J+H(g)
WJ(g)=(1−g∑JαJyJ)yJ+H(g)W^J(g)=(1-\frac{g}{\sum_J\alpha^Jy^J})y^J+H(g)

Each group's ideal policy is given by

H_g(g) = y^J/(\sum_J\alpha^Jy^J)
Hg(g)=yJ/(∑JαJyJ)H_g(g) = y^J/(\sum_J\alpha^Jy^J)

Size of government

Median voter's ideal policy

H_g(g) = y^M/y
Hg(g)=yM/yH_g(g) = y^M/y

will be the equilibrium in the Downsian model

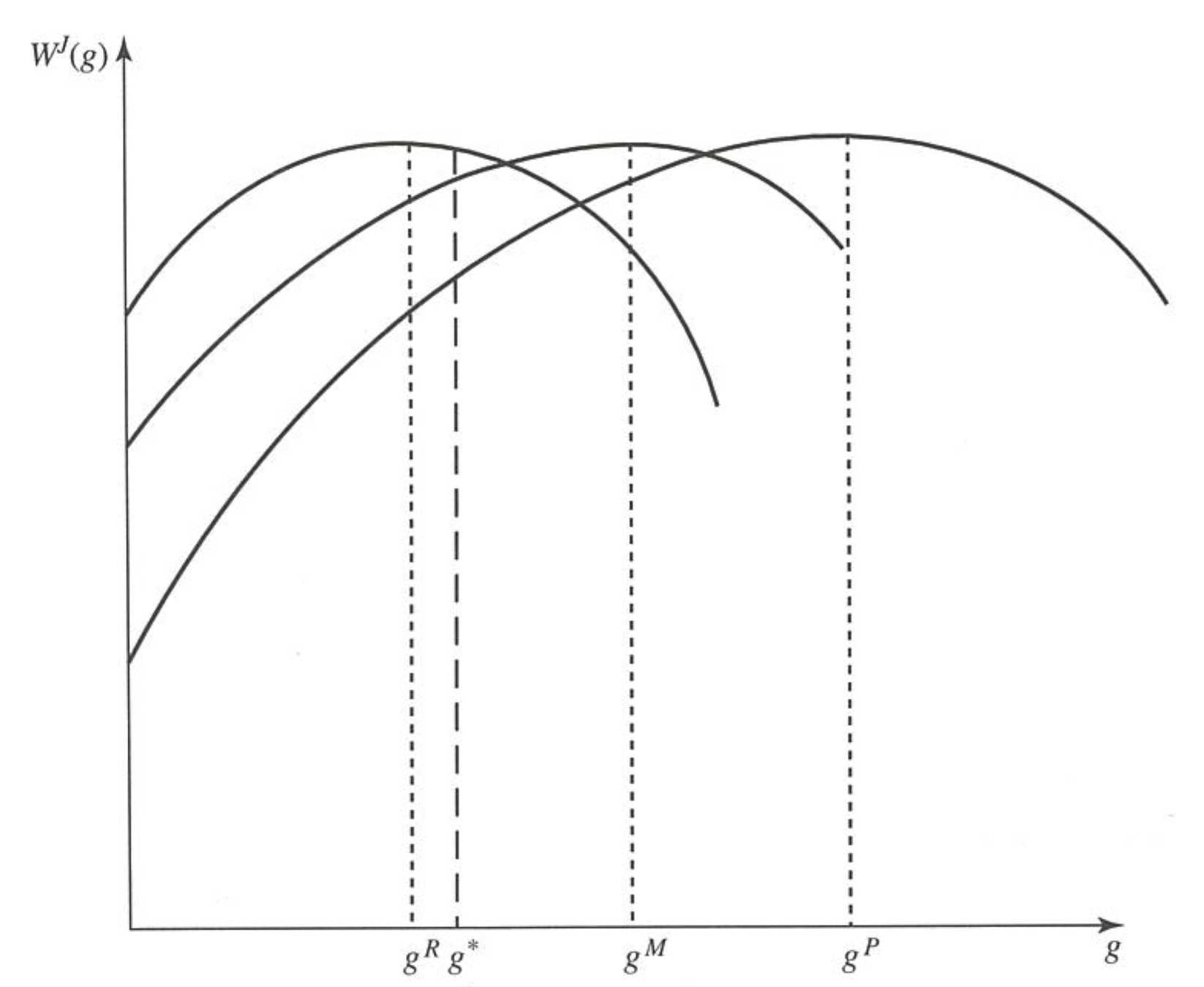
Figure 3.2 of Persson and Tabellini (2000)

Size of government

Median voter's ideal policy

H_g(g) = y^M/y
Hg(g)=yM/yH_g(g) = y^M/y

will be the equilibrium in the Downsian model

Size of government

Candidate's problem

\max_{g_A}p_AR
maxgApAR\max_{g_A}p_AR
p_A=\frac{1}{2}+\frac{\psi}{\phi}\sum_J\alpha^J\phi^J(W^J(g_A)-W^J(g_B))
pA=12+ψϕ∑JαJϕJ(WJ(gA)−WJ(gB))p_A=\frac{1}{2}+\frac{\psi}{\phi}\sum_J\alpha^J\phi^J(W^J(g_A)-W^J(g_B))

where

That is, 

\max_{g_A}\frac{\psi}{\phi}\sum_J\alpha^J\phi^JW^J(g_A)
maxgAψϕ∑JαJϕJWJ(gA)\max_{g_A}\frac{\psi}{\phi}\sum_J\alpha^J\phi^JW^J(g_A)
W^J(g)=(1-\frac{g}{\sum_J\alpha^Jy^J})y^J+H(g)
WJ(g)=(1−g∑JαJyJ)yJ+H(g)W^J(g)=(1-\frac{g}{\sum_J\alpha^Jy^J})y^J+H(g)

where

Candidate's problem (cont.)

\max_{g_A}\frac{\psi}{\phi}\sum_J\alpha^J\phi^JW^J(g_A)
maxgAψϕ∑JαJϕJWJ(gA)\max_{g_A}\frac{\psi}{\phi}\sum_J\alpha^J\phi^JW^J(g_A)
=\frac{\psi}{\phi}\sum_J\alpha^J\phi^J[(1-\frac{g_A}{\sum_J\alpha^Jy^J})y^J+H(g_A)]
=ψϕ∑JαJϕJ[(1−gA∑JαJyJ)yJ+H(gA)]=\frac{\psi}{\phi}\sum_J\alpha^J\phi^J[(1-\frac{g_A}{\sum_J\alpha^Jy^J})y^J+H(g_A)]

FOC w.r.t. \(g_A\)

\sum_J\alpha^J\phi^JH_g(g_A)=\frac{1}{\sum_J\alpha^Jy^J}\sum_J\alpha^J\phi^Jy^J
∑JαJϕJHg(gA)=1∑JαJyJ∑JαJϕJyJ\sum_J\alpha^J\phi^JH_g(g_A)=\frac{1}{\sum_J\alpha^Jy^J}\sum_J\alpha^J\phi^Jy^J
H_g(g_A)=\frac{1}{\sum_J\alpha^Jy^J}(\sum_J\alpha^J\phi^Jy^J/\sum_J\alpha^J\phi^J)
Hg(gA)=1∑JαJyJ(∑JαJϕJyJ/∑JαJϕJ)H_g(g_A)=\frac{1}{\sum_J\alpha^Jy^J}(\sum_J\alpha^J\phi^Jy^J/\sum_J\alpha^J\phi^J)

Size of government

FOC w.r.t. \(g_A\)

H_g(g_A)=\frac{1}{\sum_J\alpha^Jy^J}(\sum_J\alpha^J\phi^Jy^J/\sum_J\alpha^J\phi^J)
Hg(gA)=1∑JαJyJ(∑JαJϕJyJ/∑JαJϕJ)H_g(g_A)=\frac{1}{\sum_J\alpha^Jy^J}(\sum_J\alpha^J\phi^Jy^J/\sum_J\alpha^J\phi^J)

This term gets closer to \(y^M\)

if \(\phi^M\) is higher than the average

Otherwise,

the equilibrium policy can be far away from the median voter's ideal

Implication 3:

Median voters are not necessarily decisive

Evidence

Empirical challenge

How can we measure "swing voters"?

The literature often uses

winning margin in the previous election

But it's endogenous to distributive policies

The incumbent narrowly won maybe because voters complain about the lack of distributions

(see Larcinese et al. 2013 for a survey and criticism)

(In Lecture 4, we'll see such a model of politics)

And distribution policies are persistent over time

Evidence from Sierra Leone

Casey (2015) overcomes this difficulty

by exploiting ethnic allegiance to political parties in Sierra Leone

Image source: www.bbc.com/news/world-africa-14094194

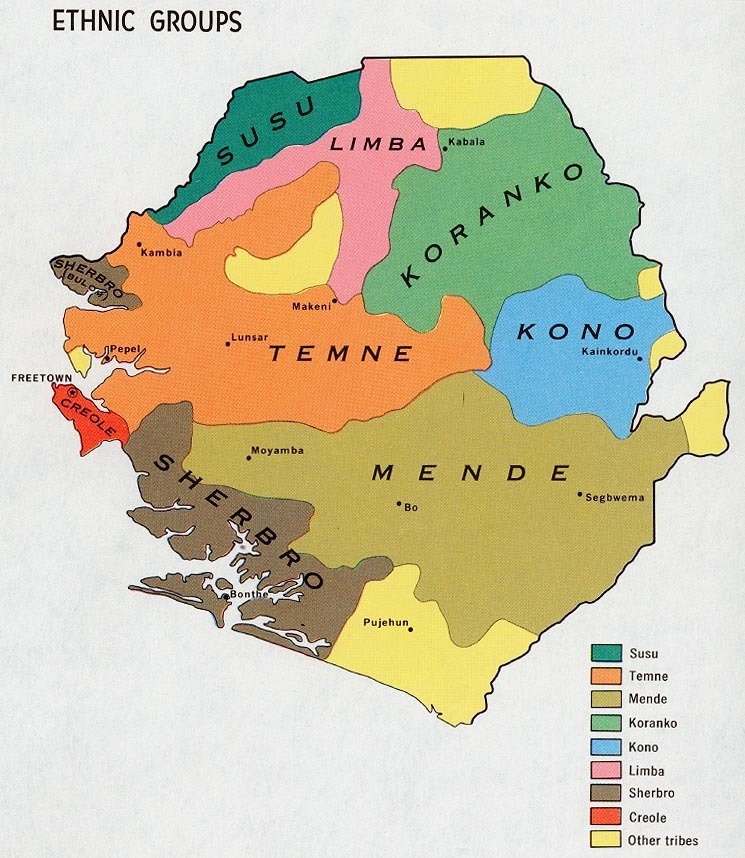
Ethnic groups in Sierra Leone

Image source: www.lib.utexas.edu/maps/africa/sierra_leone_ethnic_1969.jpg

Various ethnic groups live in different parts of the country

Political parties in Sierra Leone

Image sources: www.sierraloaded.com/apc-candidate-vows-to-win-constiuency-050-bye-election/  

www.thesierraleonetelegraph.com/?p=5780

SLPP

APC

Two parties have dominated politics since independence in 1961

Measuring ethnic allegiance to parties

Calculate each ethnic group's bias towards APC by:

% of those

who voted for

APC

% of those

who voted for

SLPP

-

Based on nation-wide voting data (for 2007 presidential election)

(not the district-level, which is a response to district-targeting policy)

Data on voting

Exit polls on local council election day in 2008

1117 voters in 59 randomly selected jurisdictions

Household surveys in 2008

6300 citizens in 634 census enumeration areas

(a nationally representative sample)

In both surveys, respondents report which party they voted

in 2007 presidential election

Take the average vote share from both surveys

Table 1 of Casey (2015)

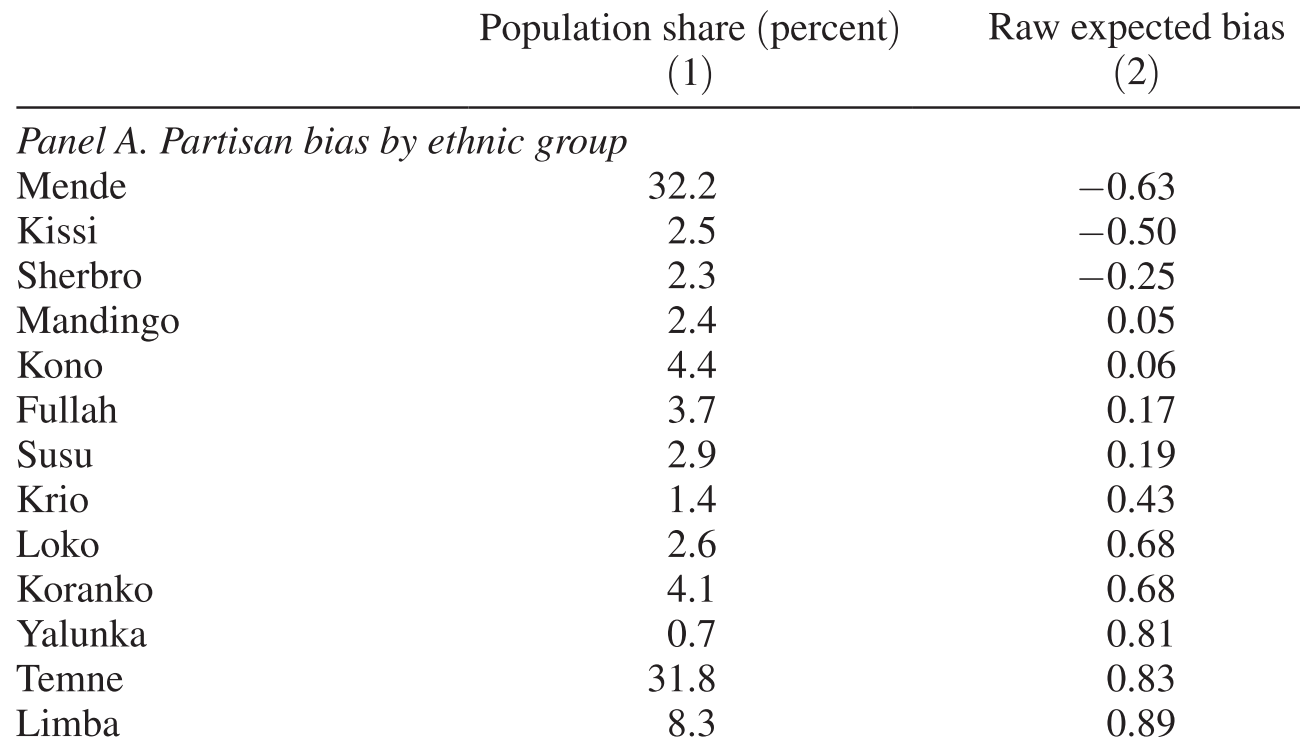
Ethnicity

Population share (%)

Bias to APC

Loyal to APC

Loyal to SLPP

Swing voters

Ethnicity predicts which party to vote

Since ethnicity cannot be changed, 

Ethnicity can be used as

a measure of voters' ideology 

that's NOT a response to policy !

Measuring swing voter districts

|\alpha_j| = |\sum_e \pi_{ej} \alpha_e|
∣αj∣=∣∑eπejαe∣|\alpha_j| = |\sum_e \pi_{ej} \alpha_e|
\pi_{ej}
πej\pi_{ej}

Population share of ethnic group e in jurisdiction j

\alpha_e
αe\alpha_e

Ethnic group e's bias towards ALC

(based on 2004 census)

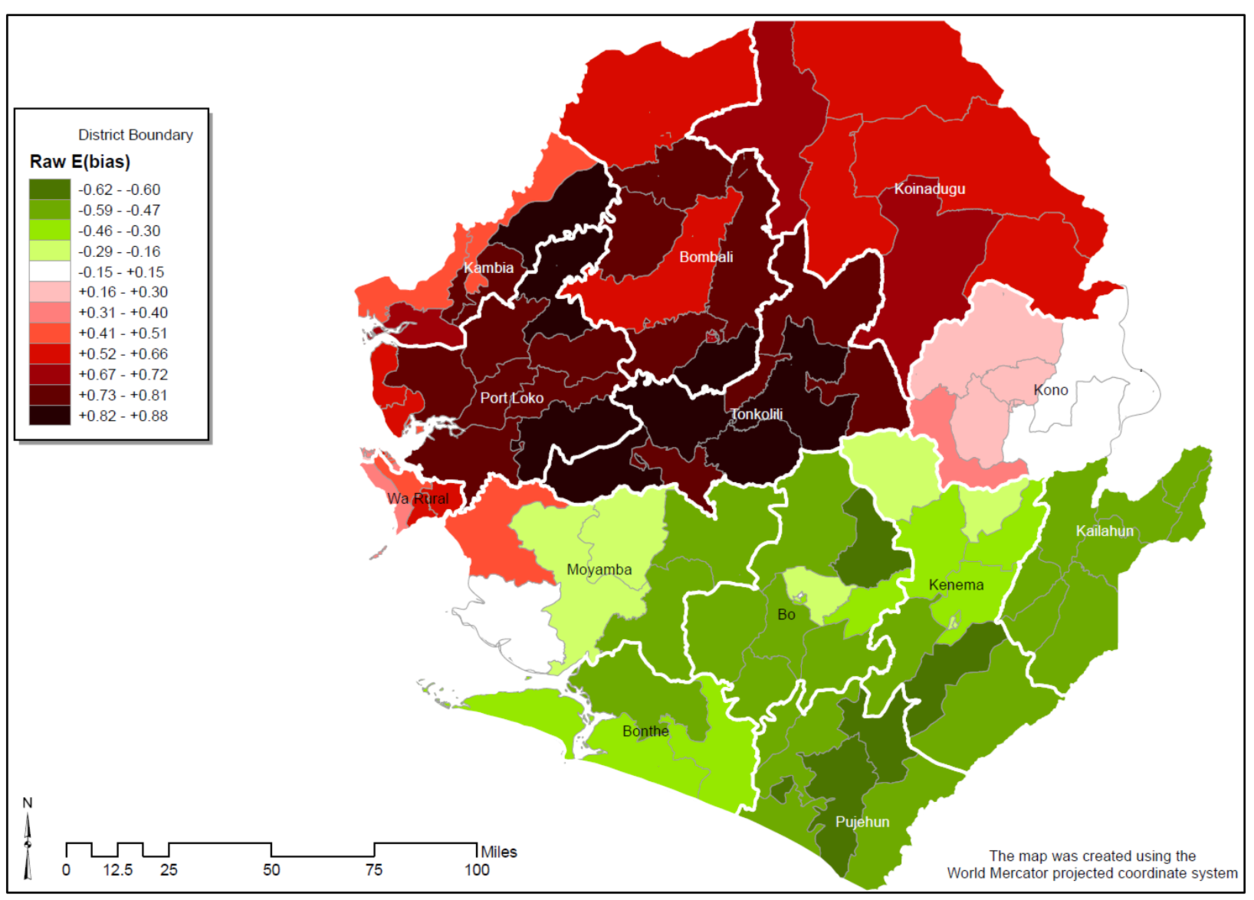
Appendix Figure 1 of Casey (2015)

Light-coloured areas: swing districts

Empirical strategy

Y^i_{jd}=\beta_0 + \beta_1|\alpha_j|+\mathbf{X}'_j\mathbf{\Gamma}+d_d+\varepsilon^i_{jd}
Yjdi=β0+β1∣αj∣+Xj′Γ+dd+εjdiY^i_{jd}=\beta_0 + \beta_1|\alpha_j|+\mathbf{X}'_j\mathbf{\Gamma}+d_d+\varepsilon^i_{jd}

Estimate the following equation by OLS:

Y^i_{jd}
YjdiY^i_{jd}

Party i's policy for jurisdiction j in district d

|\alpha_j|
∣αj∣|\alpha_j|

Bias to either of the parties

\mathbf{X}'_j
Xj′\mathbf{X}'_j

Vector of jurisdiction j's characteristics

d_d
ddd_d

District fixed effect

Measure of party policy #1

Electoral campaign spendings during the national elections

in 2007

Image source: photoblog.nbcnews.com/_news/2012/11/15/15197633-sierra-leone-president-eyes-new-term-amid-mining-boom

Measure of government policy #2

Local Government Development Grants (LGDG) during 2004-2007

Fiscal transfer from central to local governments

Spent on roads, agriculture, etc.

Image sources: www.advocacyinitiative.org and www.standardtimespress.org/artman/publish/article_4591.shtml

Check linearity assumption

Y^i_{jd}=\beta_0 + \sum_{k=1}^{34} \beta^k_1 D^k_j+\mathbf{X}'_j\mathbf{\Gamma}+d_d+\varepsilon^i_{jd}
Yjdi=β0+∑k=134β1kDjk+Xj′Γ+dd+εjdiY^i_{jd}=\beta_0 + \sum_{k=1}^{34} \beta^k_1 D^k_j+\mathbf{X}'_j\mathbf{\Gamma}+d_d+\varepsilon^i_{jd}

Divide the distribution of \(|\alpha_j|\) into 35 groups with equal frequencies

Let \(D_j^k\) indicate jurisdictions falling into the \(k\)th group

Estimate the following regression by OLS

Then plot the estimated \(\beta_1^k\)'s

Source: Figure 1 of Casey (2015)

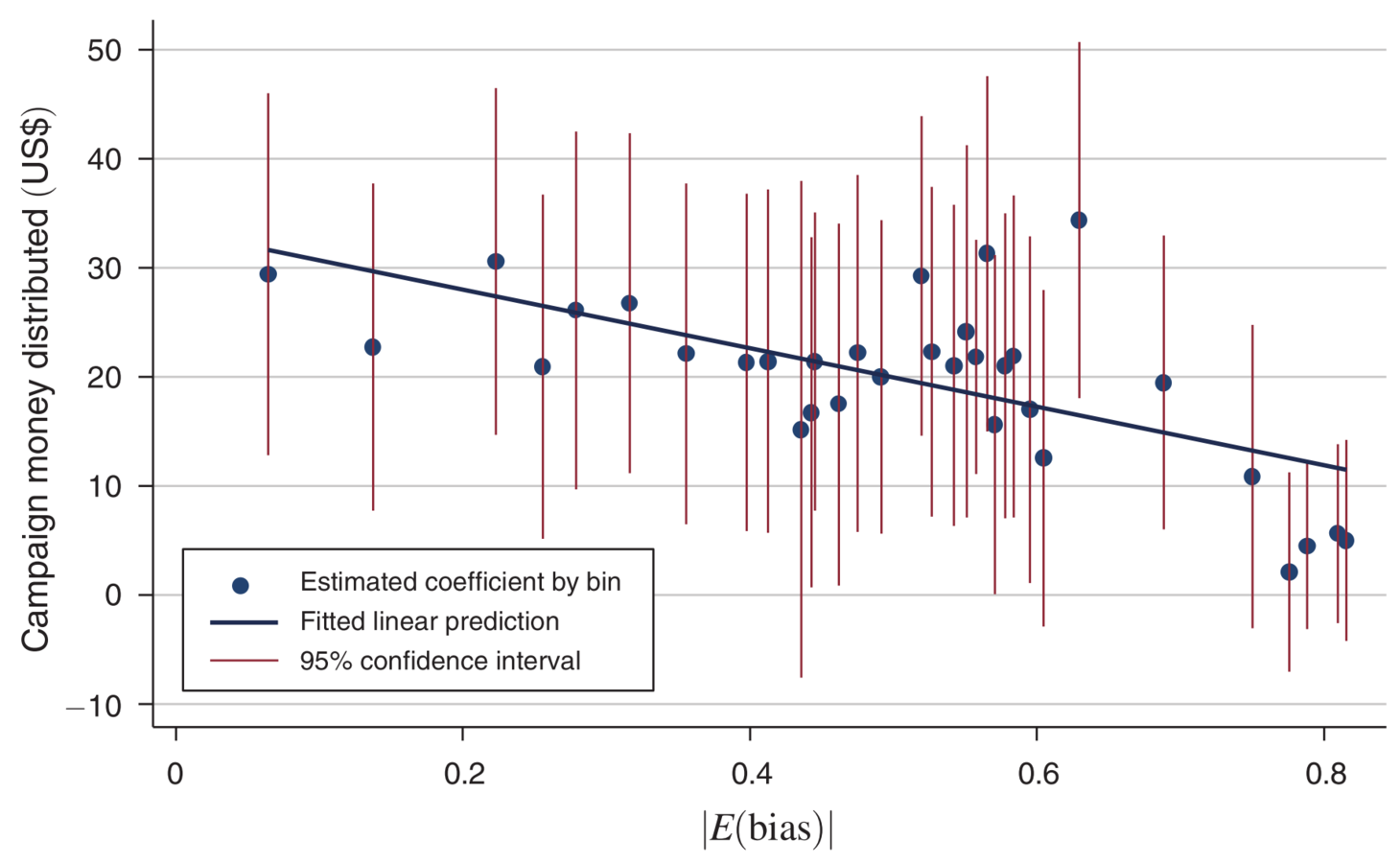
Swing districts attract campaign spendings

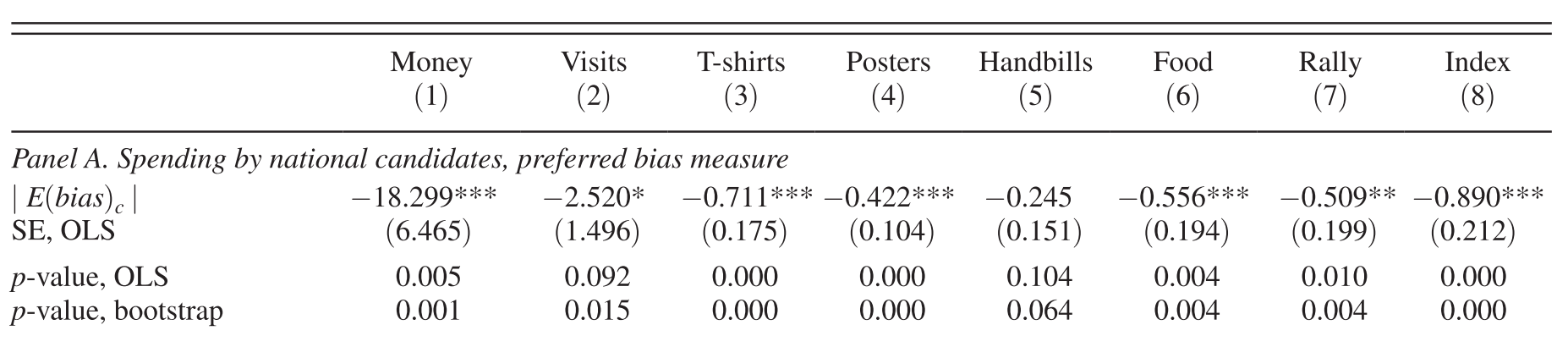
Source: Table 2 of Casey (2015)

Swing districts attract various campaign efforts

Similar results for fiscal transfer

If the bias goes down from maximum to minimum

$19,575

(8,757)

reduction in transfer

Source: page 2430 of Casey (2015)

Source: Table 2 of Casey (2015)

Inference on multiple outcomes

It's time for econometrics...

Inference on multiple outcomes (cont.)

For example, if you have 20 outcomes

the estimated treatment effect

can be statistically significant at the 5% level

for at least 1 outcome by chance

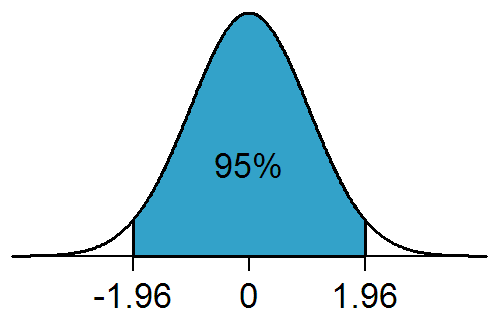
Statistical significance for each outcome is misleading

Inference on multiple outcomes (cont.)

The current standard practice is what Kling et al. (2007) proposed

Transform each outcome into a z-score

z_i^m=\frac{y^m_i - \mu^m}{\sigma^m}
zim=yim−μmσmz_i^m=\frac{y^m_i - \mu^m}{\sigma^m}

1

Take a simple unweighted average across related outcomes

2

Z_i=\frac{\sum_m z^m_i}{\# m}
Zi=∑mzim#mZ_i=\frac{\sum_m z^m_i}{\# m}

3

Estimate the treatment effect on this average z-score

Source: Table 2 of Casey (2015)

Inference on multiple outcomes

Interpretation

Moving from maximum (0) to minimum (1) swing-ness

Campaign efforts go up by 0.89 standard deviation

Applications

Application #1: Incorporate candidate quality

Citizen i of group J votes for A if

W^J(\mathbf{q}_A)>W^J(\mathbf{q}_B)+\sigma^{iJ}+\delta
WJ(qA)>WJ(qB)+σiJ+δW^J(\mathbf{q}_A)>W^J(\mathbf{q}_B)+\sigma^{iJ}+\delta

Casey (2015) interprets \(\delta\) as the relative quality of candidate B

In the basic model, remember:

Its variance gets smaller if citizens are more informed of candidates

Then targeting such citizens is more effective to gain votes

Application #2: Voter intimidation

In the local public good distribution example...

H_g(g_A^J)=\frac{\sum_I\alpha^I\phi^I}{\phi^J}
Hg(gAJ)=∑IαIϕIϕJH_g(g_A^J)=\frac{\sum_I\alpha^I\phi^I}{\phi^J}

Swing voters (i.e. high \(\phi^J\)) are "expensive to buy"

In countries like Zimbabwe where incumbent politicians 

Consume government revenue

Can intimidate voters from voting

It may pay for incumbents to intimidate swing voters

so they can consume more

Robinson and Torvik (2009) argue...

Other applications for empirical research

Stromberg (2008 AER)

Electoral campaign across states by US presidential candidates

Galasso and Nannicini (2011 APSR)

Candidate selection by parties across districts in Italy

Impact of radio on New Deal policy in the 1930s US

Stromberg (2004 QJE)

Other applications for theoretical research

Lizzeri and Persico (2004 QJE)

Cause of democratization

Hassler et al. (2005 JME)

Fahri et al. (2012 Restud)

Song et al. (2012 Econometrica)

Dynamic voting in a macroeconomic model

One more application:

Impact of electoral rules

on the composition of government spending

Persson and Tabellini (1999)

See also Chapter 8 of Persson and Tabellini (2000)

Model

Players

Three groups of voters

J\in\{1,2,3\}
J∈{1,2,3}J\in\{1,2,3\}

Each group has a continuum of voters with unit mass

Two political parties

A,B
A,BA,B

(So the total population size is 3)

Each lives in its own district

Citizens' preference

Member i of group J

f_A^J+H(g_A)
fAJ+H(gA)f_A^J+H(g_A)

Transfer to district J

Public

good

f_B^J+H(g_B)+\sigma^{iJ}+\delta
fBJ+H(gB)+σiJ+δf_B^J+H(g_B)+\sigma^{iJ}+\delta

if candidate A wins

if candidate B wins

Citizens' preference (cont.)

Population-wide popularity shock for B

\delta
δ\delta

uniformly distributed between 

[-\frac{1}{2\psi},\frac{1}{2\psi}]
[−12ψ,12ψ][-\frac{1}{2\psi},\frac{1}{2\psi}]

Individual ideology for member i of group J

\sigma^{iJ}
σiJ\sigma^{iJ}

uniformly distributed between 

[-\frac{1}{2\phi^J}+\bar{\sigma}^J,\frac{1}{2\phi^J}+\bar{\sigma}^J]
[−12ϕJ+σ¯J,12ϕJ+σ¯J][-\frac{1}{2\phi^J}+\bar{\sigma}^J,\frac{1}{2\phi^J}+\bar{\sigma}^J]

with 

\bar{\sigma}^1 < \bar{\sigma}^2=0 < \bar{\sigma}^3
σ¯1<σ¯2=0<σ¯3\bar{\sigma}^1 < \bar{\sigma}^2=0 < \bar{\sigma}^3

and

\phi^2=\max_j[\phi^J]
ϕ2=maxj[ϕJ]\phi^2=\max_j[\phi^J]

Graphically...

\sigma^{iJ}
σiJ\sigma^{iJ}
\phi^3
ϕ3\phi^3
\phi^2
ϕ2\phi^2
\phi^1
ϕ1\phi^1
\bar{\sigma}^2(=0)
σ¯2(=0)\bar{\sigma}^2(=0)
\bar{\sigma}^1
σ¯1\bar{\sigma}^1
\bar{\sigma}^3
σ¯3\bar{\sigma}^3

Policies

f^J
fJf^J

Transfer to district J   (e.g. roads, schools, hospitals)

g
gg

Public good   (e.g. national defence, social protection)

which satisfy the government budget constraint

\sum_Jf^J+g \leq T
∑JfJ+g≤T\sum_Jf^J+g \leq T

Exogenous govt revenue

Political party's preference & action

p_PR
pPRp_PR

Each party P maximizes

by committing to a policy vector

\mathbf{q}_P=[ g, \{f^J\}] \geq \mathbf{0}
qP=[g,{fJ}]≥0\mathbf{q}_P=[ g, \{f^J\}] \geq \mathbf{0}

Timing of Events

1

2

3

4

Parties A and B simultaneously announce

their policy platform

\mathbf{q}_A, \mathbf{q}_B
qA,qB\mathbf{q}_A, \mathbf{q}_B

Nature picks both individual (\(\sigma^{iJ}\)) and aggregate (\(\delta\)) popularity shocks for B

Citizens decide which party to vote for

Electoral rule determines each party's seat share

in legislature

5

The party with the majority of seats forms the government

to implement the announced policy

Electoral rules

Single-district election

(proportional representation)

Multi-district election

(majoritarian)

with sufficiently small \(\bar{\sigma}^1\) and sufficiently large \(\bar{\sigma}^3\) 

Denote A's vote share among group J voters by

\pi_{A,J}
πA,J\pi_{A,J}

Party A wins the majority of seats if

\frac{1}{3}\sum_J\pi_{A,J}\geq\frac{1}{2}
13∑JπA,J≥12\frac{1}{3}\sum_J\pi_{A,J}\geq\frac{1}{2}
\pi_{A,2}\geq\frac{1}{2}
πA,2≥12\pi_{A,2}\geq\frac{1}{2}

This is an example of how we can model political institutions

Focus on some features of political institutions

Model them as the rule of the game / the game structure

In this course, we will see more examples:

Term Limit (Lecture 4)

Presidential vs Parliamentary systems (Lecture 5)

Equilibrium

for Single-district Election

District transfer

f^2>0, f^1=f^3=0
f2>0,f1=f3=0f^2>0, f^1=f^3=0

Targeting district 2 brings more votes

\sigma^{iJ}
σiJ\sigma^{iJ}
\phi^3
ϕ3\phi^3
\phi^2
ϕ2\phi^2
\phi^1
ϕ1\phi^1
\Delta f^2
Δf2\Delta f^2
\Delta f^3
Δf3\Delta f^3
\Delta f^1
Δf1\Delta f^1

Public good

\sum_J\phi^JH_g(g^*)=\phi^2
∑JϕJHg(g∗)=ϕ2\sum_J\phi^JH_g(g^*)=\phi^2
\sigma^{iJ}
σiJ\sigma^{iJ}
\phi^3
ϕ3\phi^3
\phi^2
ϕ2\phi^2
\phi^1
ϕ1\phi^1
H_g(g)\Delta g
Hg(g)ΔgH_g(g)\Delta g
H_g(g)\Delta g
Hg(g)ΔgH_g(g)\Delta g
H_g(g)\Delta g
Hg(g)ΔgH_g(g)\Delta g

Vote gains by \(\Delta g\)

Public good

\sum_J\phi^JH_g(g^*)=\phi^2
∑JϕJHg(g∗)=ϕ2\sum_J\phi^JH_g(g^*)=\phi^2
\sigma^{iJ}
σiJ\sigma^{iJ}
\phi^3
ϕ3\phi^3
\phi^2
ϕ2\phi^2
\phi^1
ϕ1\phi^1
\Delta f^2(=\Delta g)
Δf2(=Δg)\Delta f^2(=\Delta g)

Vote loss by \(\Delta g\)

Public good in the equilibrium

H_g(g^*)=\phi^2 / \sum_J\phi^J
Hg(g∗)=ϕ2/∑JϕJH_g(g^*)=\phi^2 / \sum_J\phi^J
\sigma^{iJ}
σiJ\sigma^{iJ}
\phi^3
ϕ3\phi^3
\phi^2
ϕ2\phi^2
\phi^1
ϕ1\phi^1
H_g(g)\Delta g
Hg(g)ΔgH_g(g)\Delta g
H_g(g)\Delta g
Hg(g)ΔgH_g(g)\Delta g
H_g(g)\Delta g
Hg(g)ΔgH_g(g)\Delta g
\Delta f^2(=\Delta g)
Δf2(=Δg)\Delta f^2(=\Delta g)

Equilibrium

for Multiple-district Election

Only district 2 can be swung

\sigma^{iJ}
σiJ\sigma^{iJ}
\phi^3
ϕ3\phi^3
\phi^2
ϕ2\phi^2
\phi^1
ϕ1\phi^1
\sigma^2
σ2\sigma^2
\sigma^1
σ1\sigma^1
\sigma^3
σ3\sigma^3

District transfer

f^2>0, f^1=f^3=0
f2>0,f1=f3=0f^2>0, f^1=f^3=0

For districts 1 and 3, the electoral result does not depend on f

Public good

\phi^2H_g(g^*)=\phi^2
ϕ2Hg(g∗)=ϕ2\phi^2H_g(g^*)=\phi^2
\sigma^{iJ}
σiJ\sigma^{iJ}
\phi^3
ϕ3\phi^3
\phi^2
ϕ2\phi^2
\phi^1
ϕ1\phi^1
H_g(g)\Delta g
Hg(g)ΔgH_g(g)\Delta g

Vote gain by \(\Delta g\)

Public good

\phi^2H_g(g^*)=\phi^2
ϕ2Hg(g∗)=ϕ2\phi^2H_g(g^*)=\phi^2
\sigma^{iJ}
σiJ\sigma^{iJ}
\phi^3
ϕ3\phi^3
\phi^2
ϕ2\phi^2
\phi^1
ϕ1\phi^1

Vote loss by \(\Delta g\)

\Delta g=\Delta f^2
Δg=Δf2\Delta g=\Delta f^2

Public good in the equilibrium

H_g(g^*)=1
Hg(g∗)=1H_g(g^*)=1
\sigma^{iJ}
σiJ\sigma^{iJ}
\phi^3
ϕ3\phi^3
\phi^2
ϕ2\phi^2
\phi^1
ϕ1\phi^1
\Delta g=\Delta f^2
Δg=Δf2\Delta g=\Delta f^2
H_g(g)\Delta g
Hg(g)ΔgH_g(g)\Delta g

Comparison of

the two electoral rules

Public good provision

Multi-district majoritarian elections

H_g(g^*)=1
Hg(g∗)=1H_g(g^*)=1

Single-district (proportional representation) elections

H_g(g^*)=\phi^2 / \sum_J\phi^J
Hg(g∗)=ϕ2/∑JϕJH_g(g^*)=\phi^2 / \sum_J\phi^J
<1
<1<1

Equilibrium policy

g^*
g∗g^*

smaller in multi-district elections

Other theoretical models

(Lizzeri and Persico 2001, Milesi-Ferretti et al. 2002)

derive similar predictions:

Composition of government expenditure is tilted to

group specific transfers 

under

majoritarian elections

public good / universal welfare 

under

proportional representation

Impact of electoral rules

on the size of government spending

Austen-Smith (2000) and Milesi-Ferretti et al. (2002) predict

Majoritarian elections lead to a smaller government

Evidence

Causal evidence?

Hard to prove causality running from electoral rules to policies

Electoral rules rarely change

Thus impossible to separate the impact of electoral rules

from that of country characteristics

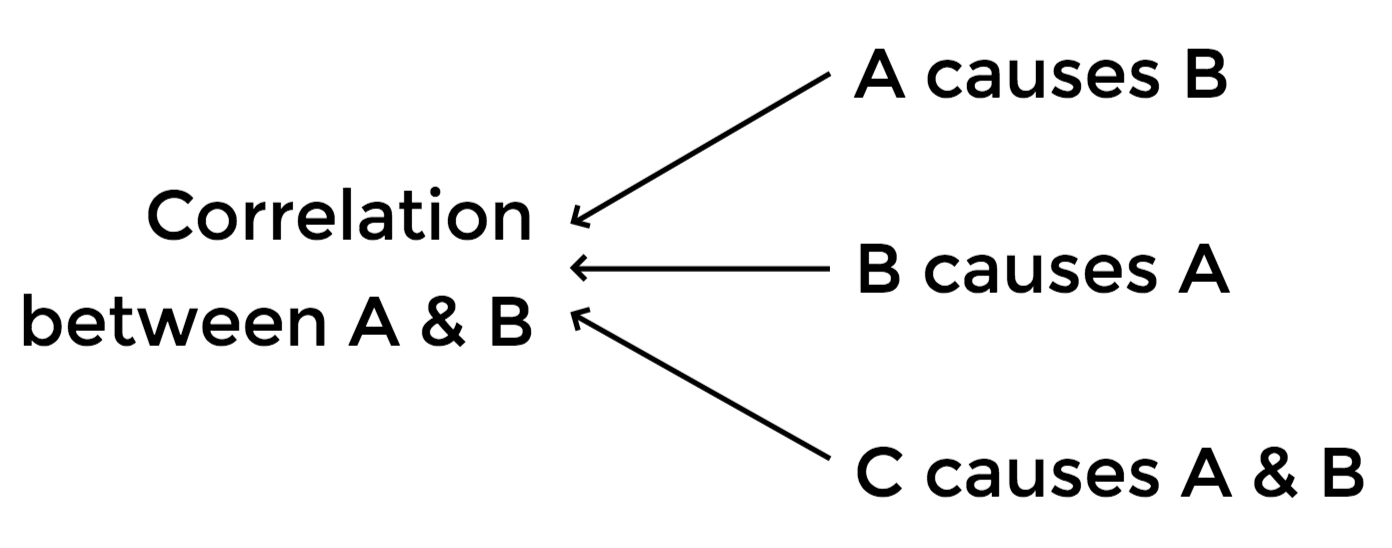
Causal evidence?

We can only check

if correlation is consistent with the theoretical prediction

Persson and Tabellini (2004)

See also Persson and Tabellini (2003) and Acemoglu (2005)

Run cross-country regressions of fiscal policies on electoral rule

y_i = \beta S_i+\mathbf{Z}_i\mathbf{\Gamma}+\varepsilon_i
yi=βSi+ZiΓ+εiy_i = \beta S_i+\mathbf{Z}_i\mathbf{\Gamma}+\varepsilon_i
\mathbf{Z}_i
Zi\mathbf{Z}_i

Per capita GDP

Trade openness

Population

% of those aged 16-54

% of those aged over 65

 

Years of being democracy

Quality of democracy (Freedom House Index)

Dummy for presidential system

Dummy for federal states

 

Dummy for OECD countries

Dummies for continents

Dummies for legal origins

Electoral rules around the world in the 1990s

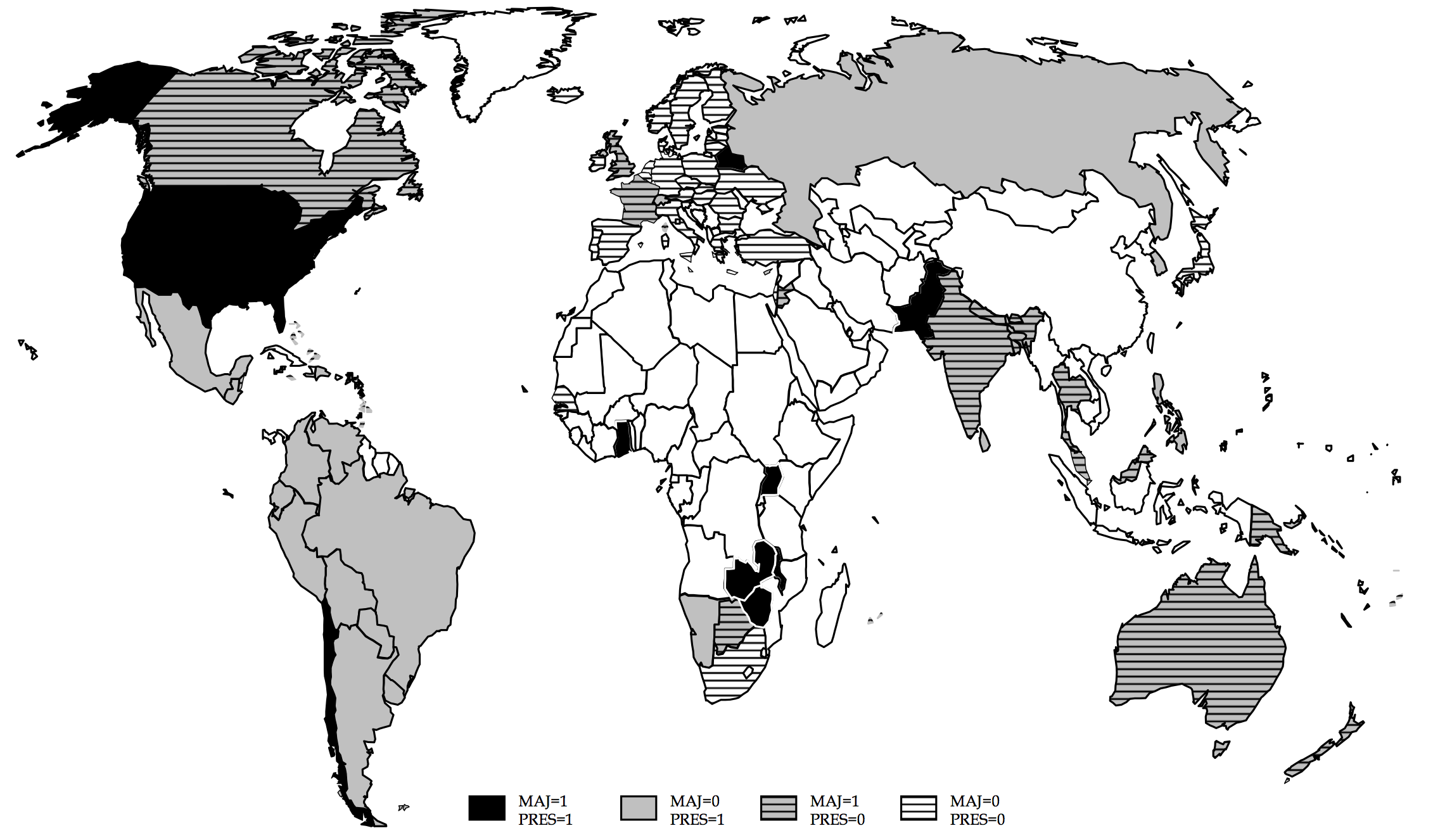
Figure 4.1 of Persson and Tabellini (2003) The Economic Effects of Constitutions

Majoritarian

Proportional Representation

Not democratic

(S_i=1)
(Si=1)(S_i=1)
(S_i=0)
(Si=0)(S_i=0)

(excluded from the sample)

Unconditional mean comparison

Fiscal policy
(as % of GDP)		 Central govt expenditure Social protection
Majoritarian 25.6%
(8.2)		 4.7%
(5.4)
Proportional representation 30.8%
(11.3)		 10.1%
(6.6)
p-value for
two-sample
t-test

Source: Table 1 of Persson and Tabellini (2004)

Note: Standard deviation in parentheses

0.03

0.00

OLS estimation results

Dep. Var.
(as % of GDP)		 Central govt expenditure Central govt revenue Government deficit Social protection
Majoritarian
elections		 -6.32***
(2.11)		 -3.68*
(2.15)		 -3.15***
(0.87)		 -2.25*
(1.25)
# observations 80 76 72 69

Source: Tables 2 and 4 of Persson and Tabellini (2004)

Countries with majoritarian elections

have a smaller size of government

spend less on social protection (pension, unemployment benefits, child allowance, etc.)

Other impacts of electoral rules

Political selection

Beath et al. (2016 Restud)

Elected politicians are more competent

under a single multi-member district

than under a multiple single-member district

Made with Slides.com