Welcome
Laurens Doedes Breuning ten Cate
Nyenrode New Business School / University of Westminster - Amsterdam & London
Business Administration (hons)
Finance & Business Innovation specialization
Planning
Pre-test
Training
Post-test
Introduction
Question
Situation # 1:
Given: The median height of an average American Male is 176cm. You are on a business trip and are scheduled to spend the night at a nice hotel down-town.
Wanted: Estimate the probability that the first male guest you see in the hotel lobby is over 176cm
Solution: 50%
Cont.
Situation # 2:
Given: On your way to the hotel you discover that the National Basketball Player's Association is having a convention in town and the official hotel is the one where you are to stay, and furthermore, they have reserved all the rooms but yours.
Wanted: Now, estimate the probability that the first male guest you see in the hotel lobby is over 176cm.
Solution: More than 50% Maybe even much more, and that's obvious too.
Bayes Rule
You just applied Bayesian Updating!
You updated your Prior probability estimate when new information became available to a Posterior probability estimate.

Formal
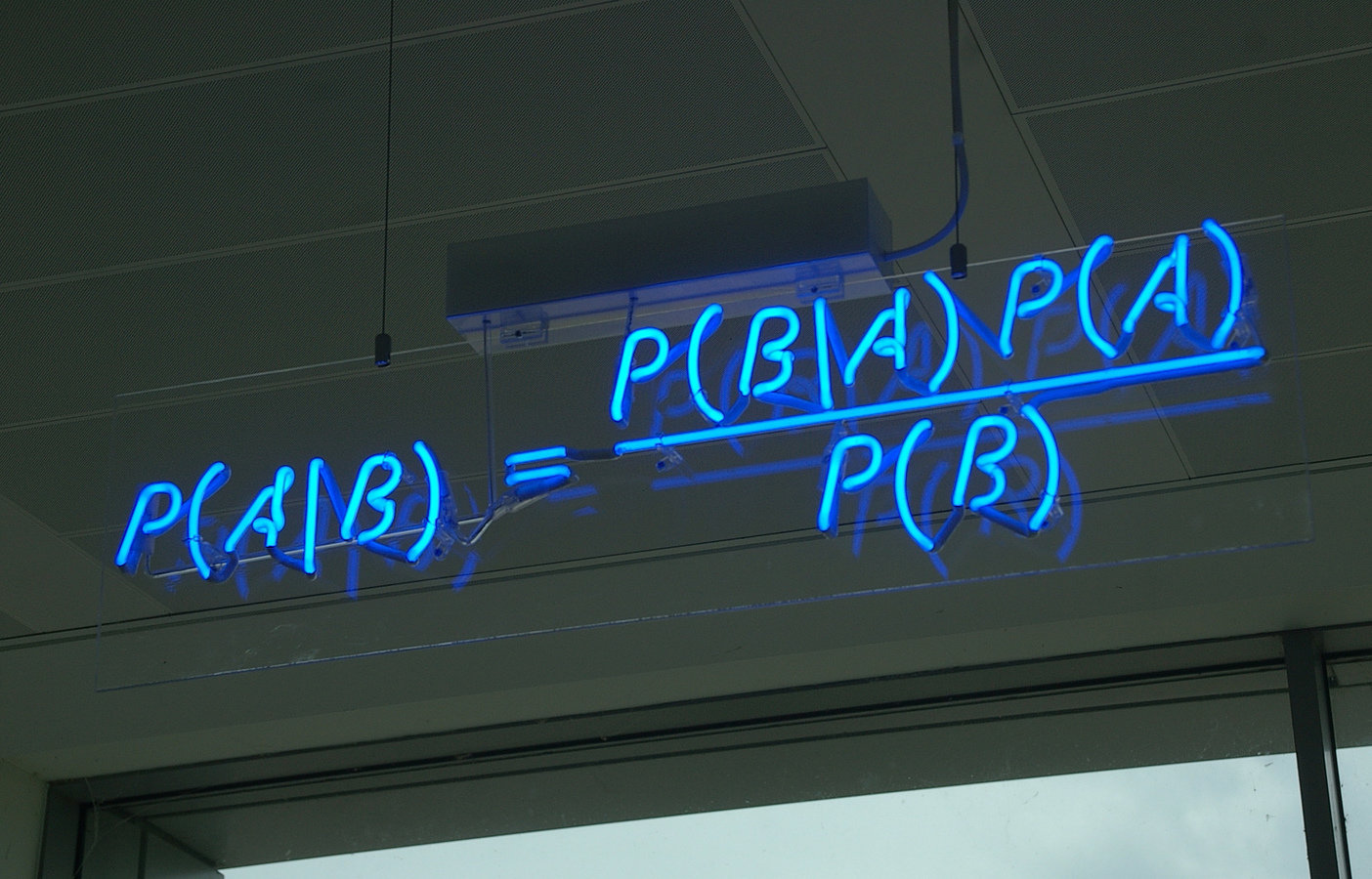
This informal 'updating' can also be done when real probabilities are known through a simple formula.
A cab was involved in a hit and run accident at night. Two cab companies, the Green and the Blue, operate in the city. 85% of the cabs in the city are Green and 15% are Blue. A witness identified the cab as Blue. The court tested the reliability of the witness under the same circumstances that existed on the night of the accident and concluded that the witness correctly identified each one of the two colours 80% of the time and failed 20% of the time.
What is the probability that the cab involved in the accident was Blue rather than Green knowing that this witness identified it as Blue?
Example
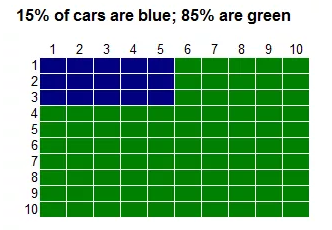
Let's visualize this
Example
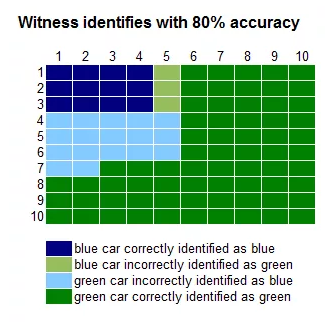
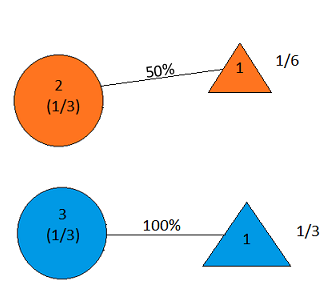
The next step is to figure out the proportion of cabs correctly and incorrectly identified. The witness is 80% accurate, which means 80% of blue cars will be identified as blue, and 80% of green cars will be identified as green. The remaining cars are incorrectly identified. Here is a diagram of that.
Example
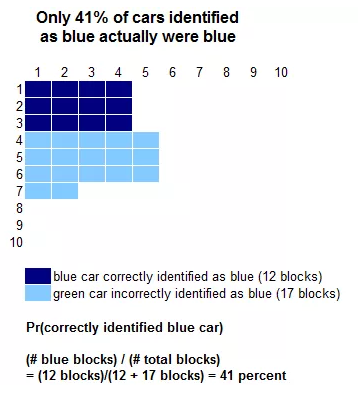
Finally, let us only focus on the cars that were identified as blue. This comes from the blue cars correctly identified and the green cars incorrectly identified. Here is the resulting figure. You’ll notice the number of cars incorrectly identified as blue is slightly larger.
Monty Hall
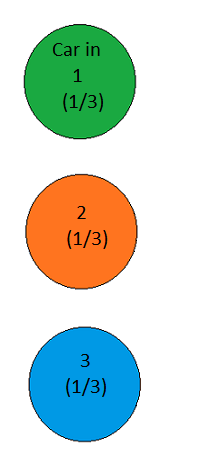
First construct 3 hypothesises
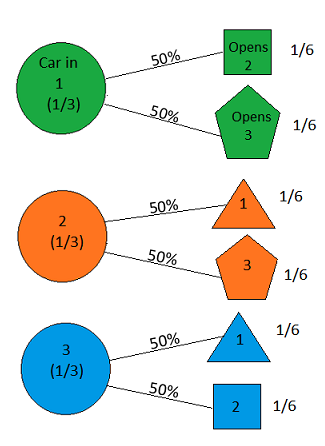
New data through action from the game-show host
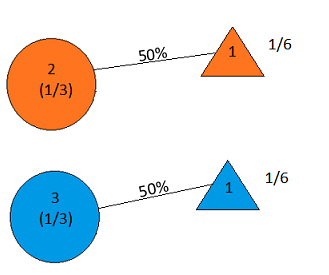
We select door 2. Host opens door 1. So 50%?
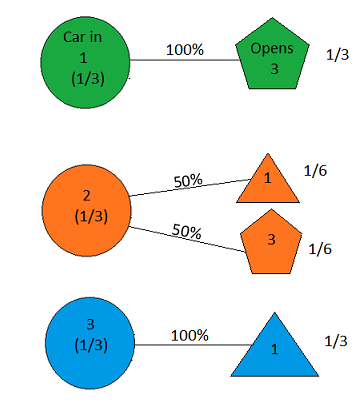
When we selected door 2 the visual representation should have looked like this.
So if the host opens door 1 we get: