BFS & DFS

LAVI

Agenda

Graph
Graph Storage
- Adjacency Matrix
- Adjacency List
Traverse
- BFS
- DFS

Graph

Definition

圖 Graph = 點 vertex 的集合 + 邊 edge 的集合
以 G = (V, E) 表示

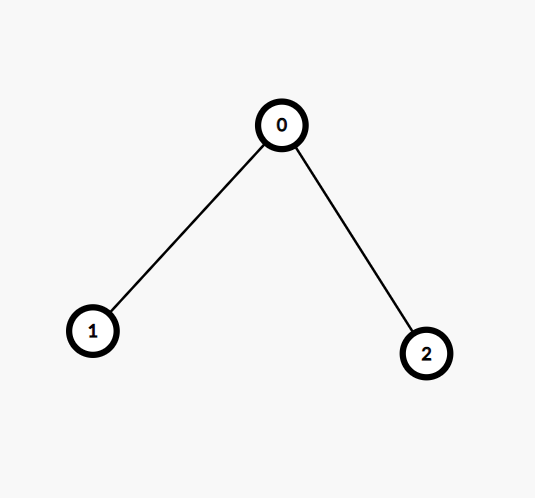
|V| = 3
|E| = 2

V = {0, 1, 2}
E = {01, 02}

Graph

有向圖 directed graph

無向圖 undirected graph

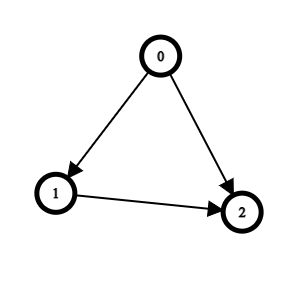
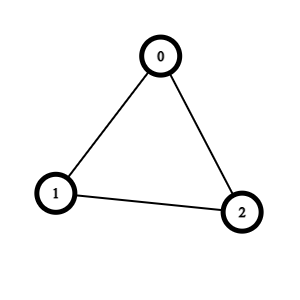
Graph

環 cycle：路徑的起點和終點相同

自環 loop：邊的起點和終點相同

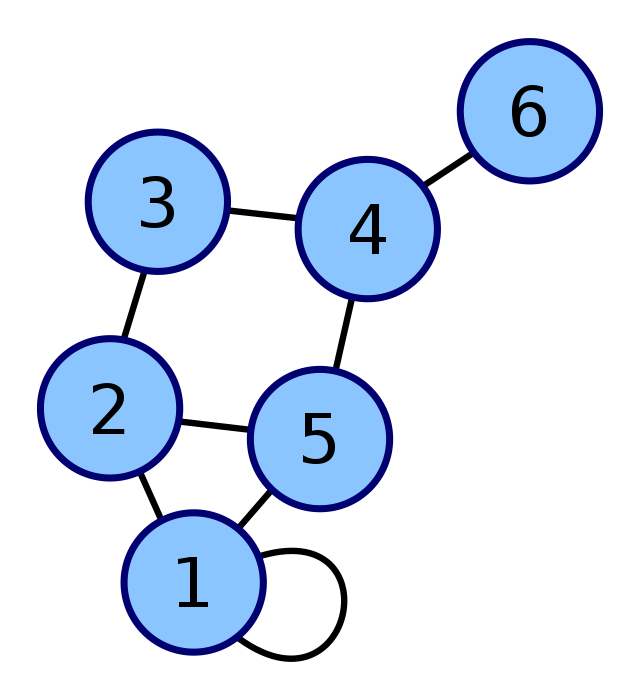
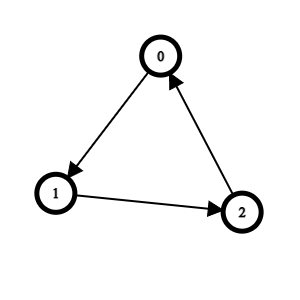
Graph

重邊 multiple edge：

在兩個點之間存在兩條以上的邊

連通 connected：

無向圖中，若點 u 與 v 之間存在路徑，則 u 和 v 連通

若一群點倆倆都連通，則這些點彼此都連通

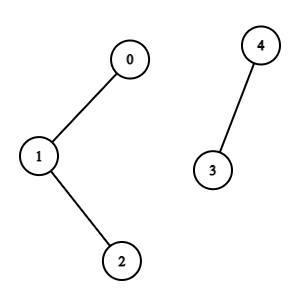
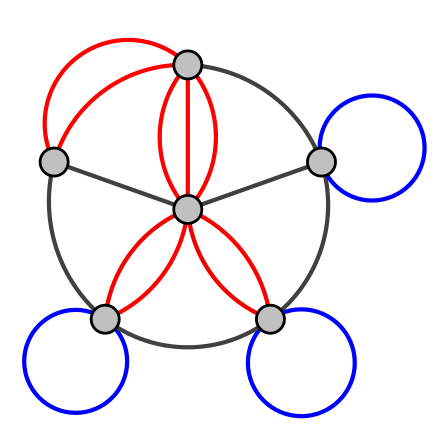
Graph

簡單圖 simple graph
- 不含重邊
- 不含自環

Graph Storage

Adjacency Matrix

使用二維陣列儲存
M[i][j] 代表點 i 到點 j 的權重

int M [v][v];
M[1][4] = 3;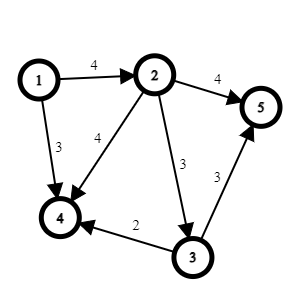

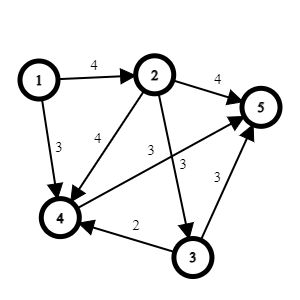
Adjacency Matrix

M = [[∞, 4, ∞, 3, ∞],
     [∞, ∞, 3, 4, 4],
     [∞, ∞, ∞, 2, ∞],
     [∞, ∞, ∞, ∞, 3]];

Adjacency Matrix

空間複雜度 O(v^2)
遍歷時間複雜度 O(v^2)
增加、刪除邊時間複雜度 O(1)
優點：方便、直觀、實作容易
缺點：在遍歷圖的時候會讀到不必要的資訊，時間複雜度較高，有可能會 TLE

# define inf 0x3f3f3f3f

int M [6][6];

for(int i = 1; i <= 5; i++){
  for(int j = 1; j <= 5; j++){
  	M[i][j] = 0;
  }
}

int start, end, weight;
while(cin >> start >> end >> weight){
  	M [start][end] = weight;
}

for(int i = 1; i <= 5; i++){
	for(int j = 1; j <= 5; j++){
		cout << M[i][j] << " ";
	}
	cout << endl;
}

Adjacency Matrix

M = [[∞, 4, ∞, 3, ∞],
     [∞, ∞, 3, 4, 4],
     [∞, ∞, ∞, 2, ∞],
     [∞, ∞, ∞, ∞, 3]];

Adjacency List

使用 vector、linkedlist 等可變換長度的資料結構儲存
在第 i 格內放著所有 i 所指向的點與權重

// no weight storage
vector<int> G[v];
G[i].push_back(j);

// weight storage
vector<pari<int, int>> G[v];
G[i].push_back(make_pair(j, w));

Adjacency List

2, 4

3, 3

4, 3

4, 4

5, 4

4, 2

5, 3

j, w

Adjacency List

空間複雜度 O(v + E)
遍歷時間複雜度 O(v + E)
增加邊時間複雜度 O(1)
修改邊時間複雜度 O(v)
優點：複雜度降低，不會浪費空間
缺點：實作複雜，刪除和修改的複雜度較高

vector<pair<int, int>> v[6];
for(int i = 1; i <=5; i++){
	v[i].clear();
}

int start, end, weight;
while(cin >> start >> end >> weight){
	v[start].push_back(make_pair(end, weight));
}

for(int i = 1; i <=5; i++){
	cout << i << " -> ";
	for(int j = 0; j < v[i].size(); j++){
		cout << v[i][j].first << " ";
        cout << v[i][j].second << " , ";
	}
	cout << endl;
}

Adjacency List

1 -> 4 3 , 2 4 , 
2 -> 3 3 , 4 4 , 5 4 ,
3 -> 4 2 , 5 3 ,
4 -> 5 3 ,
5 ->

Traverse

遍歷

遍歷就是把圖上每個點都走過一遍
方法：
- BFS 廣度優先搜尋
- DFS 深度優先搜尋

BFS

不斷找出尚未遍歷的點當作起點
- 把起點塞入 queue
- 重複以下步驟，直到 queue 裡沒有東西為止：
  1. 從 queue 中取出一點
  2. 找出與此點相鄰的點、且尚未遍歷的點，並將這些點依序塞入 queue

BFS

bool visited[12+5];
bool M[12+5][12+5];

queue<int> q;
for(int i = 0; i <= 12; i++){
	visited[i] = false;
}

int parent, child;
while(cin >> parent >> child){
	M[parent][child] = true;
}

for(int k = 0; k <= 12; k++){
	if(!visited[k]){
		q.push(k);
		visited[k] = true;
	}

	while(!q.empty()){
		int i = q.front();
		q.pop();

		for(int j = 0; j <= 12; j++){
			if(M[i][j] && !visited[j]){
				q.push(j);
				visited[j] = true;
			}
		}
	}
}

BFS

UVA 572 - Oil Deposits

有家石油公司負責探勘某塊地底下的石油含量，這塊地是矩行的

含有石油的一小塊地稱作一個 pocket，假如兩個 pocket 相連，則這兩個 pocket 屬於同一個 oil deposit

你的任務就是要找出這塊地包含幾個不同的 oil deposit

Input

輸入包含好幾組資料，每組資料的第一行有 2 個整數 m, n

m 代表這塊地的列數，n代表這塊地的行數（1 <= m, n <= 100）

接下來的 m 行是這塊地探勘的內容

'@' 代表此小塊含石油，'*'代表此小塊不含石油

當 m = 0 && n = 0 則輸入結束

UVA 572 - Oil Deposits

Output

對每組測試資料輸出 oil deposit 的數目

// 範例輸入
1 1
*
3 5
*@*@*
**@**
*@*@*
1 8
@@****@*
5 5
****@
*@@*@
*@**@
@@@*@
@@**@
0 0

// 範例輸出
0
1
2
2

int row[] = { 1, 1, 1, 0, -1, -1, -1, 0 };
int column[] = { -1, 0, 1, 1, 1, 0, -1, -1 };

void bfs( int x_now, int y_now ){

    for( int j = 0; j < 8; j++ ){

        x_next = x_now + row[j];
        y_next = y_now + column[j];

        if( x_next < m && y_next < n && x_next >= 0 && y_next >= 0 && oil[ x_next ][ y_next ] == '@' ){

            // 此點已找過 就把他改成普通地板
            oil[ x_next ][ y_next ] = '*';
            bfs( x_next, y_next );

        }
    }
    return;
}

UVA 572 - Oil Deposits

#include<bits/stdc++.h>
using namespace std;

int m, n;
int x_now, y_now, x_next, y_next;

int ans;
char oil[100][100];

int row[] = { 1, 1, 1, 0, -1, -1, -1, 0 };
int column[] = { -1, 0, 1, 1, 1, 0, -1, -1 };

void bfs( int x_now, int y_now ){

    for( int j = 0; j < 8; j++ ){

        x_next = x_now + row[j];
        y_next = y_now + column[j];

        if( x_next < m && y_next < n && x_next >= 0 && y_next >= 0 && oil[ x_next ][ y_next ] == '@' ){

            // 此點已找過 就把他改成普通地板
            oil[ x_next ][ y_next ] = '*';
            bfs( x_next, y_next );

        }
    }
    
    return;
}

int main(){

    while( cin >> m >> n && m && n ){

        memset( oil, '0', sizeof(oil) );
        ans = 0;

        for( int i = 0; i < m; i++ ){
            for( int j = 0; j < n; j++ ){
                cin >> oil[i][j];          
            }
        }

        for( int i = 0; i < m; i++ ){
            for( int j = 0; j < n; j++ ){

                if( oil[i][j] == '@' ){
                   ans++;
                   bfs( i, j );
                }
            }
        }
        cout << ans << endl;
    }
}

UVA 572 - Oil Deposits

UVA 439 - Knight Moves

你的朋友正在做關於西洋棋中騎士旅行問題（Traveling Knight Problem）的研究

他希望你幫他解決一個問題：給你 2 個格子的位置 X 及 Y

請你找出騎士從 X 走到 Y 最少需要走幾步

Input

每筆測試資料一列

每列有 2 個西洋棋的座標位置

每個位置座標是由一個英文字母（a-h，代表棋盤的第幾欄）

及一個數字（1-8，代表棋盤的第幾列）組成

UVA 439 - Knight Moves

Output

對每一列輸入

輸出：To get from xx to yy takes n knight moves.

// 範例輸入
e2 e4
a1 b2
b2 c3
a1 h8
a1 h7
h8 a1
b1 c3
f6 f6

// 範例輸出
To get from e2 to e4 takes 2 knight moves.
To get from a1 to b2 takes 4 knight moves.
To get from b2 to c3 takes 2 knight moves.
To get from a1 to h8 takes 6 knight moves.
To get from a1 to h7 takes 5 knight moves.
To get from h8 to a1 takes 6 knight moves.
To get from b1 to c3 takes 1 knight moves.
To get from f6 to f6 takes 0 knight moves.

int bfs(){
    
    chess[0][0] = letter_start;
    chess[0][1] = digit_start;
    visited[ letter_start ][ digit_start ] = true;

    for( int i = 0, knights = 1; i < knights; i++ ){
        letter_now = chess[i][0];
        digit_now = chess[i][1];

        if( letter_now == letter_end && digit_now == digit_end ){
            return step[ letter_now ][ digit_now ];
        }

        for( int j = 0; j < 8; j++ ){          
            letter_next = letter_now + column[j];
            digit_next = digit_now + row[j];

            if( letter_next < 1 || digit_next < 1 || letter_next > 8 || digit_next > 8 || visited[ letter_next ][ digit_next ] ){        
                continue;
            }

            else{
                visited[ letter_next ][ digit_next ] = true;
                step[ letter_next ][ digit_next ] = step[ letter_now ][ digit_now ] + 1;

                chess[ knights ][0] = letter_next;
                chess[ knights ][1] = digit_next;

                knights++;
            }
        }
    }
    return -1;
}

UVA 439 - Knight Moves

#include<bits/stdc++.h>
using namespace std;

char letter1, letter2;
int letter_start, digit_start, letter_end, digit_end;
int letter_now, digit_now, letter_next, digit_next;

int chess[10000+5][2], step[10][10];
bool visited[8][8];

int row[8] = { 1, 2, 2, 1, -1, -2, -2, -1 };
int column[8] = { 2, 1, -1, -2, -2, -1, 1, 2 };

int bfs(){
    
    chess[0][0] = letter_start;
    chess[0][1] = digit_start;
    visited[ letter_start ][ digit_start ] = true;

    for( int i = 0, knights = 1; i < knights; i++ ){
        letter_now = chess[i][0];
        digit_now = chess[i][1];

        if( letter_now == letter_end && digit_now == digit_end ){
            return step[ letter_now ][ digit_now ];
        }

        for( int j = 0; j < 8; j++ ){        
            letter_next = letter_now + column[j];
            digit_next = digit_now + row[j];

            if( letter_next < 1 || digit_next < 1 || letter_next > 8 || digit_next > 8 || visited[ letter_next ][ digit_next ] ){         
                continue;
            }

            else{
                visited[ letter_next ][ digit_next ] = true;
                step[ letter_next ][ digit_next ] = step[ letter_now ][ digit_now ] + 1;

                chess[ knights ][0] = letter_next;
                chess[ knights ][1] = digit_next;

                knights++;
       	    }
        }
    }
    return -1;
}

int main(){

    while( cin >> letter1 >> digit_start >> letter2 >> digit_end ){
       
        cout << "To get from " << letter1 << digit_start << " to " << letter2 << digit_end << " takes ";
   
        letter_start = letter1 - 'a' + 1;
        letter_end = letter2 - 'a' + 1;

        for( int i = 0; i < 10; i++ ){
            for( int j = 0; j < 10; j++ ){             
                step[i][j] = 0;
                visited[i][j] = false;
            }
        }
        cout << bfs() << " knight moves." << endl;
    }
}

UVA 439 - Knight Moves

UVA 10189 - Minesweeper

您玩過《踩地雷》嗎？這是一款可愛的小遊戲，遊戲的目標是找到所有 M × N 地圖內的地雷

遊戲在一個正方形中顯示一個數字，告訴您該正方形附近有多少個地雷

例如，假設下面的4×4的地圖內帶有 2 個地雷 ( 以 "*" 字元表示 )

如果我們根據上述作法，將遊戲提示數字填入，則結果將為：

每個正方形內的數字最多為 8 ( 因為最多有8個正方形相鄰 )

// 地雷
* . . .

. . . .

. * . .

. . . .

// 數字帶入周遭有多少地雷
*	1	0	0
2	2	1	0
1	*	1	0
1	1	1	0

Input

輸入將包含多組測資
每組測資第一行包含兩個整數 n 和 m ( 0 < n, m ≤ 100 )，代表地圖大小
如果 n = m = 0 代表輸入結束
接下來的n行，每行m個字元，代表整張地圖
每個安全方塊用 "." 字元表示，每個地雷方塊用 "*" 字元表示

Output

對於每組測資
輸出第一行為 "Field #k:"，k代表測資編號
接下來輸出題示後的遊戲地圖
每筆測資間請用空白行分隔

UVA 10189 - Minesweeper

// 範例輸入
4 4
*...
....
.*..
....
3 5
**...
.....
.*...
0 0

// 範例輸出
Field #1:
*100
2210
1*10
1110

Field #2:
**100
33200
1*100

UVA 10189 - Minesweeper

void bfs(int rn, int cn){   
    
    if(now == n){
        return;
    }

    for(int i = 0; i < 8; i++){
        int cx = cn + step[i][0];
        int rx = rn + step[i][1];

        if(cx >= 0 && rx >= 0){
            cnt[rx][cx]++;
        }
    }
    now++;
    bfs(edge[now].re, edge[now].ce);
}

UVA 10189 - Minesweeper

#include<bits/stdc++.h>
using namespace std;

int now, n;
char mp[100+5][100+5];
int cnt[100+5][100+5];
int step[8][2] = {{-1, -1}, {0, -1}, {1, -1}, {-1, 0}, {1, 0}, {-1, 1}, {0, 1}, {1, 1}};

struct Edge{
    int re;
    int ce;
}edge[10000+5];

void initial(){
    now = 0, n = 0;
    for(int i = 0; i <= 100; i++){
        memset(cnt[i], 0, sizeof(cnt[i]));
    }
}

void bfs(int rn, int cn){   
    
    if(now == n){
        return;
    }

    for(int i = 0; i < 8; i++){
        int cx = cn + step[i][0];
        int rx = rn + step[i][1];

        if(cx >= 0 && rx >= 0){
            cnt[rx][cx]++;
        }
    }
    now++;
    bfs(edge[now].re, edge[now].ce);
}
int main(){
    int ca = 1;
    int r, c;
    bool flag = false;
    while(cin >> r >> c && r && c){
        
        initial();
        for(int i = 0; i < r; i++){
            for(int j = 0; j < c; j++){
                cin >> mp[i][j];
                if(mp[i][j] == '*'){
                    edge[n].re = i;
                    edge[n].ce = j;
                    n++;
                }
            }
        }
        bfs(edge[0].re, edge[0].ce);

        if(flag){
            cout << endl;
        }
        cout << "Field #" << ca++ << ":" << endl;

        for(int i = 0; i < r; i++){
            for(int j = 0; j < c; j++){
                if(mp[i][j] != '*'){
                    cout << cnt[i][j];
                }
                else{
                    cout << '*';
                }
            }
            cout << endl;
        }
        flag = true;

    }
}

UVA 10189 - Minesweeper

DFS

不斷找出尚未遍歷的點當作起點
- 把起點塞入 stack
- 重複以下步驟，直到 stack 裡沒有東西為止：
  1. 從 stack 中取出一點
  2. 找出與此點相鄰的點、且尚未遍歷的點，並將這些點依序塞入 stack

DFS

int main(){

    bool visited[12+5];
    bool M[12+5][12+5];

    stack<int> st;
    for(int i = 0; i <= 12; i++){
        visited[i] = false;
    }

    int parent, child;
    while(cin >> parent >> child){
        M[parent][child] = true;
    }

    for(int k = 0; k <= 12; k++){

        if(!visited[k]){
            st.push(k);
            visited[k] = true;
        }

        while(!st.empty()){
            int i = st.top();
            st.pop();

            for(int j = 0; j <= 12; j++){
                if(M[i][j] && !visited[j]){
                    st.push(j);
                    visited[j] = true;
                }
            }
        }
    }
}

DFS - stack

bool visited[12+5];
bool M[12+5][12+5];

void dfs(int i){
    if(!visited[i]){
        return;
    }
    visited[i] = true;

    for(int j = 0; j <= 12; j++){
        if(M[i][j]){
            dfs(j);
        }
    }
}

int main(){

    for(int i = 0; i <= 12; i++){
        visited[i] = false;
    }

    int parent, child;
    while(cin >> parent >> child){
        M[parent][child] = true;
    }

    for(int k = 0; k <= 12; k++){
        dfs(k);
    }
}

DFS - recursive

UVA 441 - Lotto

你在買彩券時一定會挑你喜歡的數字吧！雖然理論上不會增加中獎機率..

我們的問題是：假設共有 49 個號碼，而你必須在你的 k （k > 6）個Lucky Number 中挑 6 個號碼作為一張彩券的數字組合

例如：你的 Lucky Number 集合是 { 1, 2, 3, 5, 8, 13, 21, 34 } 也就是說

k = 8 ，那麼你就有C ( 8, 6 ) = 28 種可能的彩券組合

你的任務是讀入 k 以及 Lucky Number 的集合，然後輸出所有可能組合

Input

每筆測試資料一行

每行的第 1 個整數代表 k（6 < k < 13）

接下來的 k 個整數代表 Lucky Number 的集合，已經按數字由小到大排好，當 k = 0 代表輸入結束

Output

對每一筆測試資料，輸出其所有可能的組合，每個組合一行

請注意輸出組合的順序需由小到大排列

測試資料之間請空一行

// 範例輸入
7 1 2 3 4 5 6 7
8 1 2 3 5 8 13 21 34
0

// 範例輸出
1 2 3 4 5 6
1 2 3 4 5 7
1 2 3 4 6 7
1 2 3 5 6 7
1 2 4 5 6 7
1 3 4 5 6 7
2 3 4 5 6 7

1 2 3 5 8 13
1 2 3 5 8 21
1 2 3 5 8 34
1 2 3 5 13 21
1 2 3 5 13 34
1 2 3 5 21 34
1 2 3 8 13 21
1 2 3 8 13 34
1 2 3 8 21 34
1 2 3 13 21 34
1 2 5 8 13 21
1 2 5 8 13 34
1 2 5 8 21 34
1 2 5 13 21 34
1 2 8 13 21 34
1 3 5 8 13 21
1 3 5 8 13 34
1 3 5 8 21 34
1 3 5 13 21 34
1 3 8 13 21 34
1 5 8 13 21 34
2 3 5 8 13 21
2 3 5 8 13 34
2 3 5 8 21 34
2 3 5 13 21 34
2 3 8 13 21 34
2 5 8 13 21 34
3 5 8 13 21 34

UVA 441 - Lotto

void dfs( int depth, int now ){

    // 題目要求每 6 個元素做排列組合
    if( depth == 6 ){
        for( int i = 0; i < 6; i++ ){
            if( i ){
                cout << " ";
            }
            cout << ans[i];
        }
        cout << endl;
        return;
    }

    for( int i = now; i < k; i++ ){

        ans[ depth ] = input[ i ];
        dfs( depth + 1, i + 1 );

        // 當 depth = 6 後 會回來做這個 for 迴圈
        // 此時 depth = 5 回到上一次 call dfs 前的深度
        // 此時 i = i ，但因此時 for 迴圈走向下一迴 i++ 於是 i = i + 1
        // 然後將 input[i] 的值 覆蓋過 ans[5] 接著 call dfs 去輸出 再 return 回來
        // 依此類推 當 depth = 5 做完後 會到 depth = 4 ...
    }
}

UVA 441 - Lotto

#include<bits/stdc++.h>
using namespace std;

deque<int> input;
int k;
int ans[6]={0};

void dfs( int depth, int now ){

    // 題目要求每 6 個元素做排列組合
    if( depth == 6 ){
        for( int i = 0; i < 6; i++ ){
            if( i ){
                cout << " ";
            }
            cout << ans[i];
        }
        cout << endl;
        return;
    }

    for( int i = now; i < k; i++ ){

        ans[ depth ] = input[ i ];
        dfs( depth + 1, i + 1 );

        // 當 depth = 6 後 會回來做這個 for 迴圈
        // 此時 depth = 5 回到上一次 call dfs 前的深度
        // 此時 i = i ，但因此時 for 迴圈走向下一迴 i++ 於是 i = i + 1
        // 然後將 input[i] 的值 覆蓋過 ans[5] 接著 call dfs 去輸出 再 return 回來
        // 依此類推 當 depth = 5 做完後 會到 depth = 4 ...
    }
}

int main(){

    bool flag = false;
    while( cin >> k && k ){

        if( flag ){
            cout << endl;
        }

        int n;
        for( int i = 0; i < k; i++ ){          
            cin >> n;
            input.push_back(n);
        }

        // 從深度為 0 開始往下
        dfs( 0, 0 );
        flag = true;
        input.clear();
    }
}

UVA 441 - Lotto

UVA 167 - The Sultan's Successors

努比亞的蘇丹沒有子女，他要從有資格的繼承者中挑選一位繼承王位，他希望這個繼承者夠聰明，所以他決定用一個遊戲來測試這些人

他準備了一個西洋棋盤，上面每個格子中均有一個 1 到 99 的數字，他又準備了 8 個皇后棋子，現在必須將 8 個皇后放置到棋盤中，且各皇后彼此不可互相攻擊，然而這樣有不只一種放置方式，而蘇丹要挑選的就是那位可以放置 8 個皇后，並且此 8 個位置的數的和為最大的那位

你的任務就是讀入棋盤上的數，幫蘇丹算出可以放置 8 個皇后的最大的和是多少

Input

輸入的第一列有一個整數 k（k <= 20），代表以下有幾組測試資料（就是幾個棋盤）

每組測試資料有 8 列，每列有 8 個整數（介於 0 到 99），代表棋盤中格子的資料

Output

對每一組測試資料

輸出可以放置 8 個皇后的最大的和是多少

輸出長度為5，靠右對齊

// 範例輸入
2
 1  2  3  4  5  6  7  8
 9 10 11 12 13 14 15 16
17 18 19 20 21 22 23 24
25 26 27 28 29 30 31 32
33 34 35 36 37 38 39 40
41 42 43 44 45 46 47 48
48 50 51 52 53 54 55 56
57 58 59 60 61 62 63 64
99 92 53 74 69 76 87 98
 9 12 11 12 19 14 15 16
17 14 19 20 29 22 23 24
25 26 57 28 29 30 31 32
33 34 36 76 39 58 39 40
 1 42 43 44 85 46 47 48
58 60 71 82 53 34 55 56
57 58 39 90 61 32 23 44

// 範例輸出
  260
  429

UVA 167 - The Sultan's Successors

void dfs( int q ){

    // 因為每排必至少有一個皇后
    // 所以 x 直接用 q 去代，每行每行去 dfs
    if( dq[0].size() == 8 ){

        int tmp = 0;
        for( int i = 0; i < 8; i++ ){
            tmp += number[ dq[0][i] ][ dq[1][i] ];
        }
        if( tmp > sum ){
            sum = tmp;
        }
        return;
    }

    // 這個 i 是 y 因為 x 已由 q 決定 
    for( int i = 0; i < 8; i++ ){

        // 確認是否此為可放皇后
        if( check( q, i ) ){

            vis[q][i] = true;

            // 把 x y 座標分別放入 deque
            dq[0].push_back(q);
            dq[1].push_back(i);

            // 去算下一排的 q 的 y 會在哪
            dfs( q + 1 );

            // 找完回來要把剛找的那個點設為沒找過
            vis[q][i] = false;

            // 記得把 deque 裡放的點拿出來
            dq[0].pop_back();
            dq[1].pop_back();
        }
    }
}

UVA 167 - The Sultan's Successors

#include<bits/stdc++.h>
using namespace std;
// 2021.09.22

int sum;
bool vis[8][8];
int number[8][8];
deque<int> dq[2];

// 八皇后 上下左右斜行皆不重複
int check( int x, int y ){

    for( int i = 0; i < x; i++ ){
        if( dq[1][i] == y ){
            return 0;
        }

        // 如果兩皇后在同一斜線上 其斜率為 1
        // 如果 x2 - x1 == y2 - y1 -> y2 - y1 / x2 - x1 == 1
        if( abs( x - i ) == abs( dq[1][i] - y ) ){
            return 0;
        }
    }
    return 1;
}

void dfs( int q ){

    // 因為每排必至少有一個皇后
    // 所以 x 直接用 q 去代，每行每行去 dfs
    if( dq[0].size() == 8 ){

        int tmp = 0;
        for( int i = 0; i < 8; i++ ){
            tmp += number[ dq[0][i] ][ dq[1][i] ];
        }
        if( tmp > sum ){
            sum = tmp;
        }
        return;
    }

    // 這個 i 是 y 因為 x 已由 q 決定 
    for( int i = 0; i < 8; i++ ){

        // 確認是否此為可放皇后
        if( check( q, i ) ){

            vis[q][i] = true;

            // 把 x y 座標分別放入 deque
            dq[0].push_back(q);
            dq[1].push_back(i);

            // 去算下一排的 q 的 y 會在哪
            dfs( q + 1 );

            // 找完回來要把剛找的那個點設為沒找過
            vis[q][i] = false;

            // 記得把 deque 裡放的點拿出來
            dq[0].pop_back();
            dq[1].pop_back();
        }
    }
}

int main(){
    
    int t;  
    cin >> t;

    while( t-- ){

        memset( number, 0, sizeof(number) );
        memset( vis, false, sizeof(vis) );

        dq[0].clear();
        dq[1].clear();

        for( int i = 0; i < 8; i++ ){
            for( int j = 0; j < 8; j++ ){
                cin >> number[i][j];
            }
        }

        sum = 0;
        dfs( 0 );

        cout << setw(5) << sum << endl;
    }
}

UVA 167 - The Sultan's Successors

UVA 216 - Getting in Line

在此架構中，電腦被連成一串，也就是除了兩端的電腦各只連接一部電腦之外，其餘的電腦都正好連接 2 部電腦，左圖中，黑點代表電腦，且他們的位置以平面座標來表示，2 部電腦間距離以呎為單位

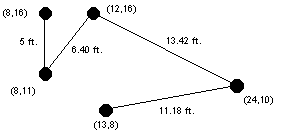
現在我們需要使連接的網路線最短，這也就是你的任務，在架設網路線時，網路線在地板下，所以相連的2部電腦所需的網路線的長度為這2部電腦的距離再加上額外的16呎，右圖顯示了上圖電腦最佳的佈線方式

其總長度為：(4+16)+ (5+16) + (5.83+16) + (11.18+16) = 90.01呎

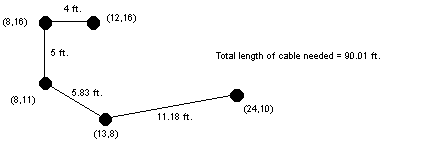
Input

輸入含有多組測試資料

每組測試資料的第一列有一個正整數 n（2 <= n <= 8），代表網路中電腦的數目，接下來的 n 列每列有 2 個介於 0 ~ 150 之間的整數，代表一部電腦的平面座標，沒有2部電腦會在同一位置

當 n = 0 代表輸入結束

Output

每組測試資料以輸出一列 * 開始，然後列出布置網路線的長度，從一端到另一端（從哪一端開始都可以），最後再列出所需的總長度，各距離均輸出到小數點後2位

UVA 216 - Getting in Line

// 範例輸出
**********************************************************
Network #1
Cable requirement to connect (5,19) to (55,28) is 66.80 feet.
Cable requirement to connect (55,28) to (28,62) is 59.42 feet.
Cable requirement to connect (28,62) to (38,101) is 56.26 feet.
Cable requirement to connect (38,101) to (43,116) is 31.81 feet.
Cable requirement to connect (43,116) to (111,84) is 91.15 feet.
Number of feet of cable required is 305.45.
**********************************************************
Network #2
Cable requirement to connect (11,27) to (88,30) is 93.06 feet.
Cable requirement to connect (88,30) to (95,38) is 26.63 feet.
Cable requirement to connect (95,38) to (84,99) is 77.98 feet.
Cable requirement to connect (84,99) to (142,81) is 76.73 feet.
Number of feet of cable required is 274.40.
**********************************************************
Network #3
Cable requirement to connect (132,73) to (72,111) is 87.02 feet.
Cable requirement to connect (72,111) to (49,86) is 49.97 feet.
Number of feet of cable required is 136.99.

UVA 216 - Getting in Line

void dfs( int depth, double path ){

    if( depth == n ){
        if( path < shortest ){
            
            shortest = path;
            final_edge.clear();
            for( int i = 0; i < n; i++ ){      
                final_edge.push_back( x_now[ i ] );
                final_edge.push_back( y_now[ i ] );
            }
        }
        return;
    }

    // 這次的 dfs 要對每個點做開關 ( true or false )
    // 在做完一趟後 直接更改 depth - 1 的點後 去對 depth 的點 ( 改變末兩點 )
    // 第二趟時 跟改 depth - 2 的點後 先依輸入順序填入後面其他點 而後下幾輪再繼續排列
    for( int i = 0; i < n; i++ ){
        
        if( flag[i] ){
            flag[i] = false;
            x_now[ depth ] = x[i];
            y_now[ depth ] = y[i];

            if( depth == 0 ){
                dfs( depth + 1, 0 );
            }
            else{
                dfs( depth + 1, path + 16 + calculate( x_now[ depth ], y_now[ depth ], x_now[ depth - 1 ], y_now[ depth - 1 ] ) );            
            }
            flag[i] = true;
        }
    }
}

UVA 216 - Getting in Line

#include<bits/stdc++.h>
using namespace std;

deque<int> x;
deque<int> y;

deque<int> x_now;
deque<int> y_now;

int n;
double shortest;

map<int, bool> flag;
deque<int> final_edge;

double calculate( int x1, int y1, int x2, int y2 ){
    
    // 計算兩點之間的距離
    // pow 次方 -> pow( 底數, 指數 )
    // sqrt 開根號 -> sqrt( 數 )
    return sqrt( pow( ( x1 - x2 ) , 2 ) + pow( ( y1 - y2 ) , 2 ) );

}

void dfs( int depth, double path ){

    if( depth == n ){
        if( path < shortest ){          
            shortest = path;
            final_edge.clear();

            for( int i = 0; i < n; i++ ){              
                final_edge.push_back( x_now[ i ] );
                final_edge.push_back( y_now[ i ] );
            }
        }
        return;
    }

    // 這次的 dfs 要對每個點做開關 ( true or false )
    // 在做完一趟後 直接更改 depth - 1 的點後 去對 depth 的點 ( 改變末兩點 )
    // 第二趟時 跟改 depth - 2 的點後 先依輸入順序填入後面其他點 而後下幾輪再繼續排列
    for( int i = 0; i < n; i++ ){

        if( flag[i] ){
            flag[i] = false;
            x_now[ depth ] = x[i];
            y_now[ depth ] = y[i];

            if( depth == 0 ){
                dfs( depth + 1, 0 );
            }
            else{
                dfs( depth + 1, path + 16 + calculate( x_now[ depth ], y_now[ depth ], x_now[ depth - 1 ], y_now[ depth - 1 ] ) );            
            }       
            flag[i] = true;
        }
    }
}

int main(){

    int num = 1;
    while( cin >> n && n ){

        int edge;

        // 先隨便設個最小值
        shortest = 2147483647;

        for( int i = 0; i < n; i++ ){

            cin >> edge;
            x.push_back(edge);

            cin >> edge;
            y.push_back(edge);

            flag.insert( pair<int, bool>( i, true ) );
        }

        dfs( 0, 0 );

        cout << "**********************************************************" << endl;
        cout << "Network #" << num << endl;

        for( int i = 0; i < ( 2 * n ) - 2; i += 2 ){
            cout << "Cable requirement to connect (" << final_edge[i] << "," << final_edge[ i + 1 ] << ") to (" << final_edge[ i + 2 ] << "," << final_edge[ i + 3 ] << ") is " << fixed << setprecision(2) << 16 + calculate( final_edge[i], final_edge[ i + 1 ], final_edge[ i + 2 ], final_edge[ i + 3 ] ) << " feet." << endl;
        }

        cout << "Number of feet of cable required is " << fixed << setprecision(2) << shortest << "." << endl;

        x.clear();
        y.clear();

        x_now.clear();
        y_now.clear();

        flag.erase( flag.begin(), flag.end() );
        final_edge.clear();

        num++;
    }
}

UVA 216 - Getting in Line

特別感謝

林子傑學長的 CPC Training
大二必修張信宏教授的資料結構、演算法
CPC 學長姊簡報資源