Common Information in Secrecy Transformation
Min-Hsiu Hsieh
University of Technology Sydney
[1] Chitambar, Fortescue, MH. Quantum Versus Classical Advantages in Secret Key Distillation. IEEE Transactions on Information Theory (accepted in June 2018).
[2] Chitambar and MH. Round Complexity in the Local Transformations of Quantum and Classical States. Nature Communications 8, no. 2086 (2017).
[3] Chitambar, Fortescue, and MH. A classical analog to entanglement reversibility. Physical Review Letters, vol. 115, p. 090501 (2015)
[4] Chitambar, Fortescue, and MH. Distributions attaining secret key at a rate of the conditional mutual information. Advances in Cryptology - CRYPTO 2015 - 35th Annual Cryptology Conference, pp. 443- 462, (2015).
Gacs-Korner Common Information
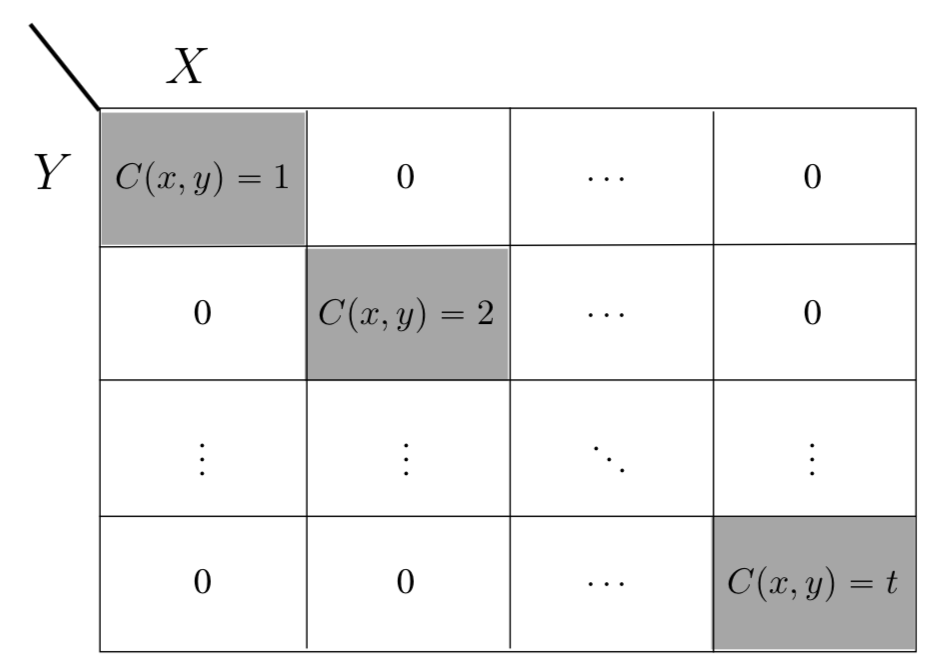
[1] Gacs and Korner, “Common information is far less than mutual information,” Problems of Control and Information Theory, vol. 2, no. 2, p. 149, 1973.
Wyner Common Information
[1] Wyner, “The common information of two dependent random variables,” IEEE Transactions on Information Theory, vol. 21, no. 2, pp. 163–179, Mar 1975.
[2] Winter, “Secret, public and quantum correlation cost of triples of random variables,” in Proceedings of International Symposium on Information Theory, 2005., Sept 2005, pp. 2270–2274.
[3] Chitambar, MH, and Winter, “The private and public correlation cost of three random variables with collaboration,” IEEE Transactions on Information Theory, vol. 62, no. 4, pp. 2034–2043, April 2016.
Extension to Tripartite
[1] Chitambar, Fortescue, and MH. A classical analog to entanglement reversibility. Physical Review Letters, vol. 115, p. 090501 (2015)
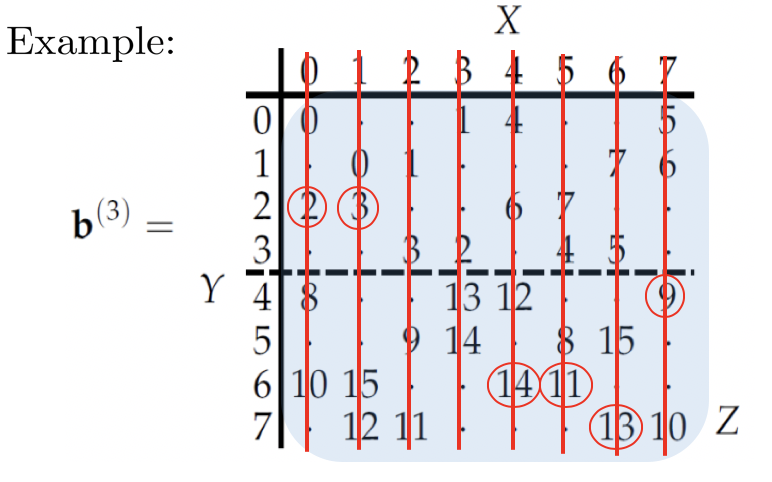
Maximal conditional common variable
Conditional Common Information
coarse-grained
Conditional Common Information
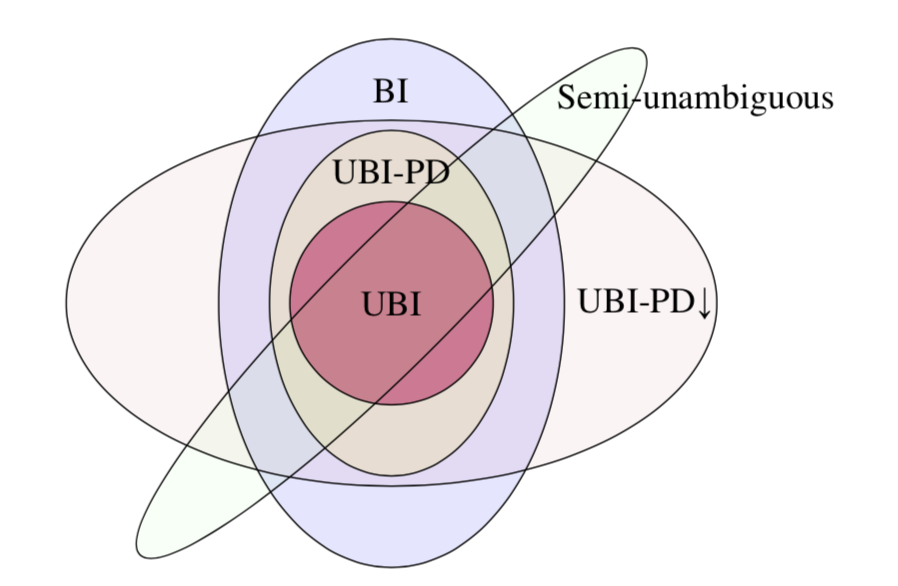
Classes of Tripartite Distributions
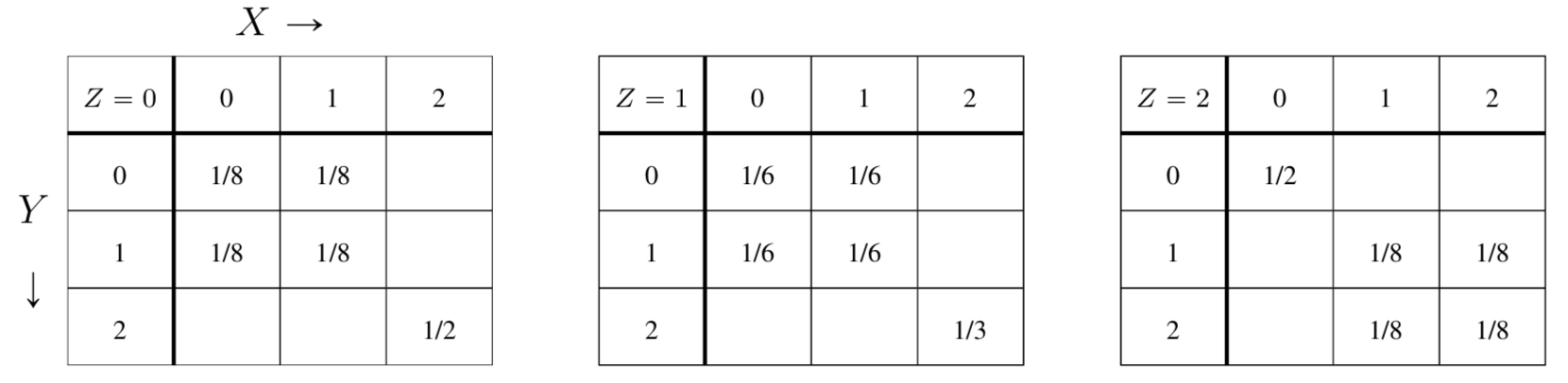
Block Independent (BI) Distributions
Classes of Tripartite Distributions
Uniform Block Independent (UBI) Distributions
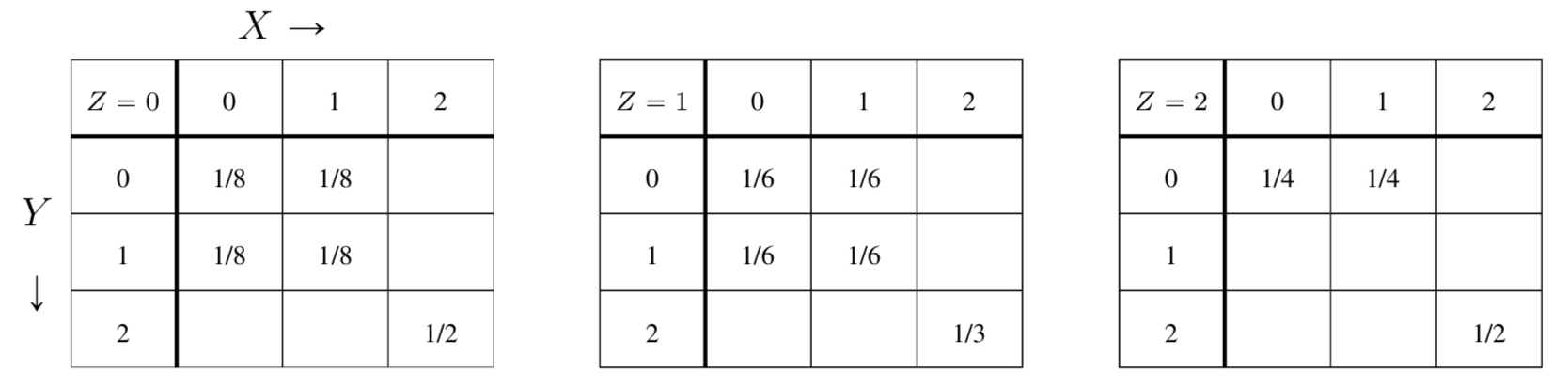
Classes of Tripartite Distributions
Uniform block independent under public discussion (UBI-PD)
\(\exist M\) s.t. \(P_{(MX)(MY)(MZ)}\) is UBI
\(I(M:J_{XY|Z}|Z)=0\)
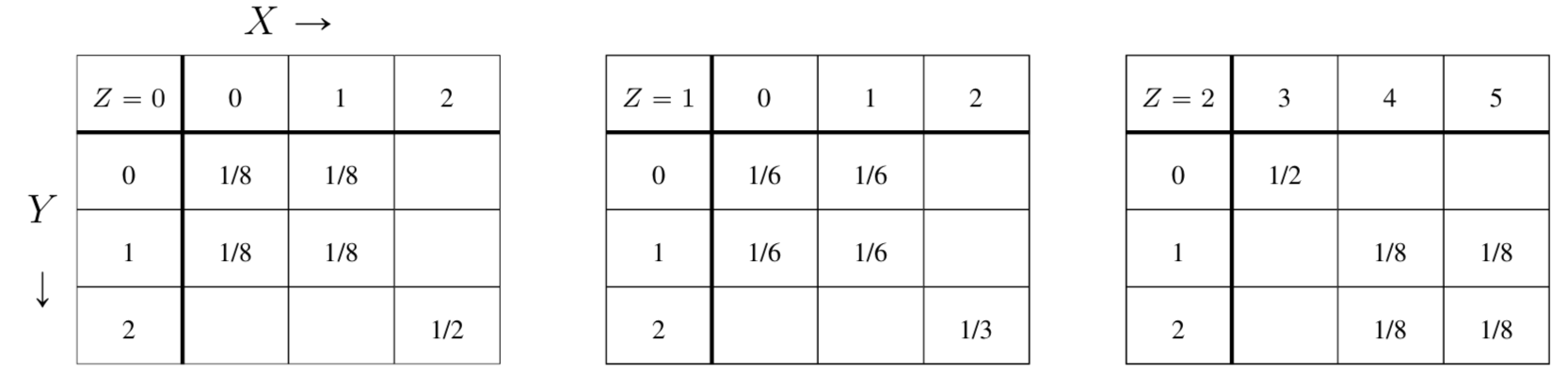
Classes of Tripartite Distributions
Uniform block independent under public discussion and eavesdropper’s local processing (UBI-PD\(\downarrow\))
\(\exist M, \bar{Z}|Z\) s.t. \(P_{XY|\bar{Z}}\) is UBI
\(I(Z:J_{XY|\bar{Z}}|M\bar{Z})=0\)
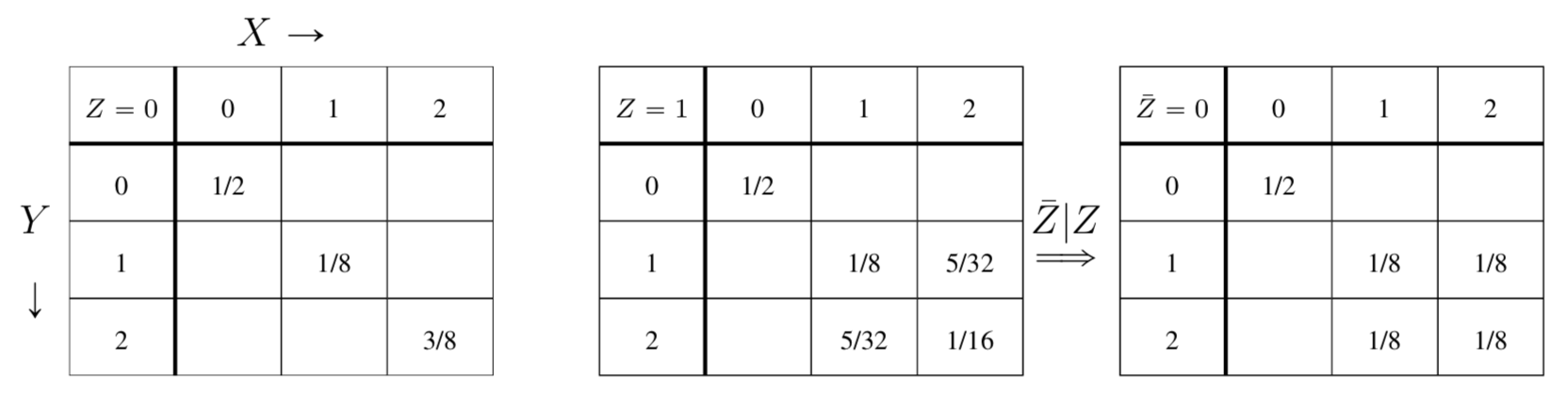
Classes of Tripartite Distributions
Semi-unambiguous
\(H(Z|XY)=0\)
[1] Christandl, Ekert, Horodecki, Horodecki, Oppenheim, and Renner, “Unifying classical and quantum key distillation,” in Theory of Cryptography, vol. 4392, pp. 456–478.
Unambiguous
\(H(Z|XY)=0\) & \(H(XY|J_{XY|Z}Z)=0\)
[2] Ozols, Smith, and Smolin, “Bound entangled states with a private key and their classical counterpart,” Phys. Rev. Lett., vol. 112, p. 110502, Mar 2014.
Classes of Tripartite Distributions
Reversible Secrecy

Determine which \(p_{XYZ}\) yielding \(K_D(X:Y|Z)= K_C(X:Y|Z)\)
-
\(K_D(X:Y|Z)\) is Open!
-
\(K_C(X:Y|Z)=\)
\(\min\{I(XY:V|U):\text{XY-Z-U},\text{X-UV-Y}\}\)
[1] Winter, “Secret, public and quantum correlation cost of triples of random variables,” in Proceedings of International Symposium on Information Theory, 2005., Sept 2005, pp. 2270–2274.
\(K_D(X:Y|Z)\leq I(X:Y\downarrow Z)\leq K_C(X:Y|Z)\)
where \(I(X:Y\downarrow Z)=\min_{\bar{Z}|Z} I(X:Y|\bar{Z})\)
[2] Renner and Wolf, in Advances in Cryptology, EUROCRYPT 2003, pp. 562–577.
If \(\min\{|\mathcal{X}|,|\mathcal{Y}|\}=2\), then \(K_D(X:Y|Z)= K_C(X:Y|Z)\) iff \(p_{XYZ}\) is UBI-PD\(\downarrow\).
[1] Chitambar, Fortescue, and MH. A classical analog to entanglement reversibility. Physical Review Letters, vol. 115, p. 090501 (2015)
If \(|\mathcal{X}|=|\mathcal{Y}|=2\), then \(K_D(X:Y|Z)= K_C(X:Y|Z)\) iff \(p_{XYZ}\) is UBI.
Open Question:
What state \(\rho_{AB}\) yields \(E_D(\rho)=E_C(\rho)\)?
Classical and Quantum Key Distillation
[1] Chitambar, Fortescue, MH. Quantum Versus Classical Advantages in Secret Key Distillation. IEEE Transactions on Information Theory (accepted in June 2018).
Quantum Embedding
How does \(K_D(\Psi_{qqq})\) compare with \(K_D(p_{XYZ})\)/\(K_D(\rho_{ccc})\)?
\(K_D(p_{XYZ})\)=\(K_D(\rho_{ccc})\)
Show that every quantum LOCC protocol can be transformed into a LOPC protocol.
\(K_D(\Psi_{qqq})\) ? \(K_D(p_{XYZ})\)
The gap can be made arbitrarily large by increasing the number of copies.
Quantum Embedding
- \(K_D(p_{XYZ})\): Classical Key Capacity
- \(K_D(\Psi_{ABBE})\): Quantum Key Capacity
- \(E_D(\rho)\): Distillable Entanglement
- \(E_C(\rho)\): Entanglement Cost
- \(E_F(\rho)\): Entanglement Formation
- \(E_r(\rho)\): Relative entropy of entanglement
- \(E_{sq}(\rho)\): squash entanglement
If \(p_{XYZ}\) is reversible, then \(K_D(p_{XYZ})\geq E_{sq}(\rho^{AB})\)
If reversible, then \(\exist \ \bar{Z}|Z\) such that \(p_{XY\bar{Z}}\) is BI.
If \(p_{XYZ}\) is UBI-PD, then \(K_D(p_{XYZ})\geq E_F(\rho^{AB})\)
\(K_D(p_{XYZ})=H(J_{XY|Z}|Z)\)
If \(p_{XYZ}\) is reversible and Semi-unambiguous ,
then \(K_D(p_{XYZ})= E_{sq}(\cdot)=K_D(\Psi_{qqq})\)
If semi-unambiguous, then \(E_{sq}(\rho^{AB})\geq K_D(\Psi_{qqq})\geq K_D(p_{XYZ})\)
[2] Ozols, Smith, and Smolin, “Bound entangled states with a private key and their classical counterpart,” Phys. Rev. Lett., vol. 112, p. 110502, Mar 2014.
If \(p_{XYZ}\) is UBI-PD and Semi-unambiguous,
then all quantities are equal to \(H(J_{XY|Z}|Z)\)
Round Complexity
What Tasks Demonstrate a Separation between \(r-1\) and \(r\) round LOCC/LOPC?
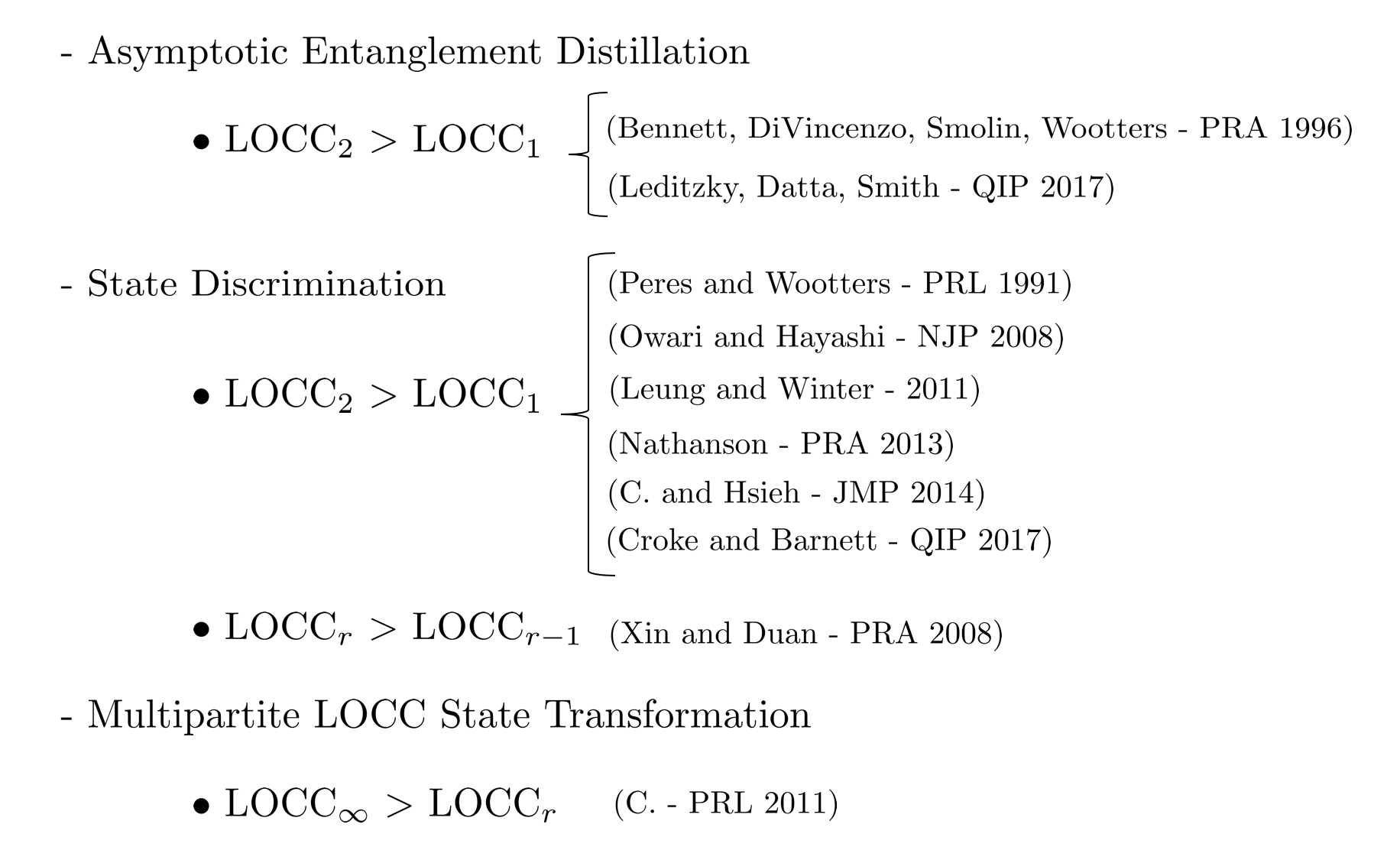
An Example that Fails to Separate the Rounds
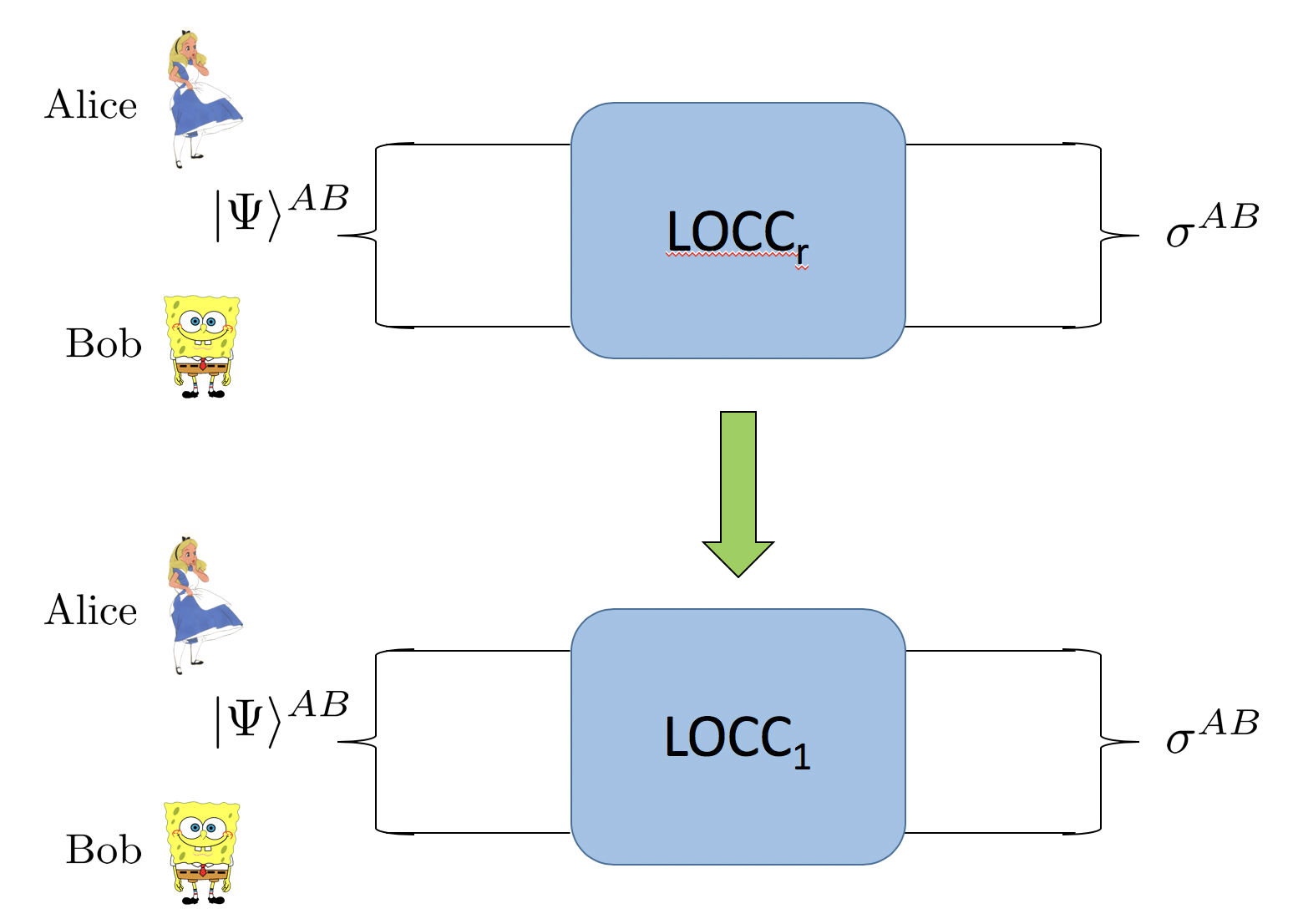
[1] Lo and Popescu, "Concentrating entanglement by local actions: Beyond mean values", Phys. Rev. A 63, 022301
For every \(r\), there exists \(\rho_r\) needing \(r\)-round LOCC to achieve \(\rho_r\to|\phi\rangle\)
Construction
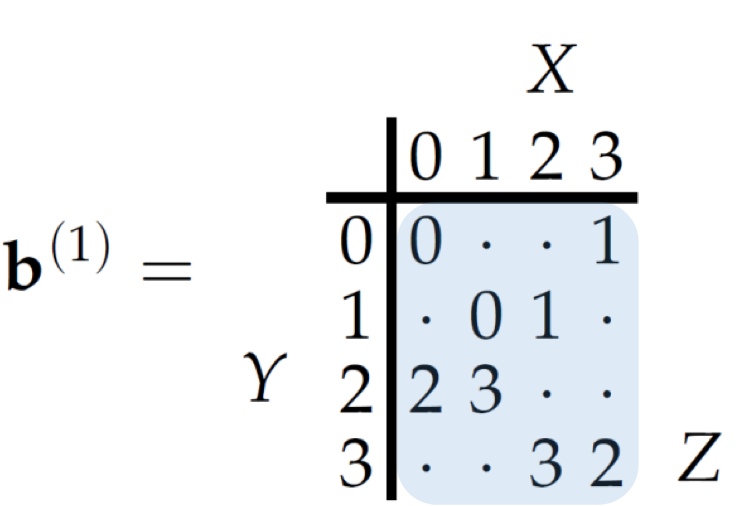
Construction
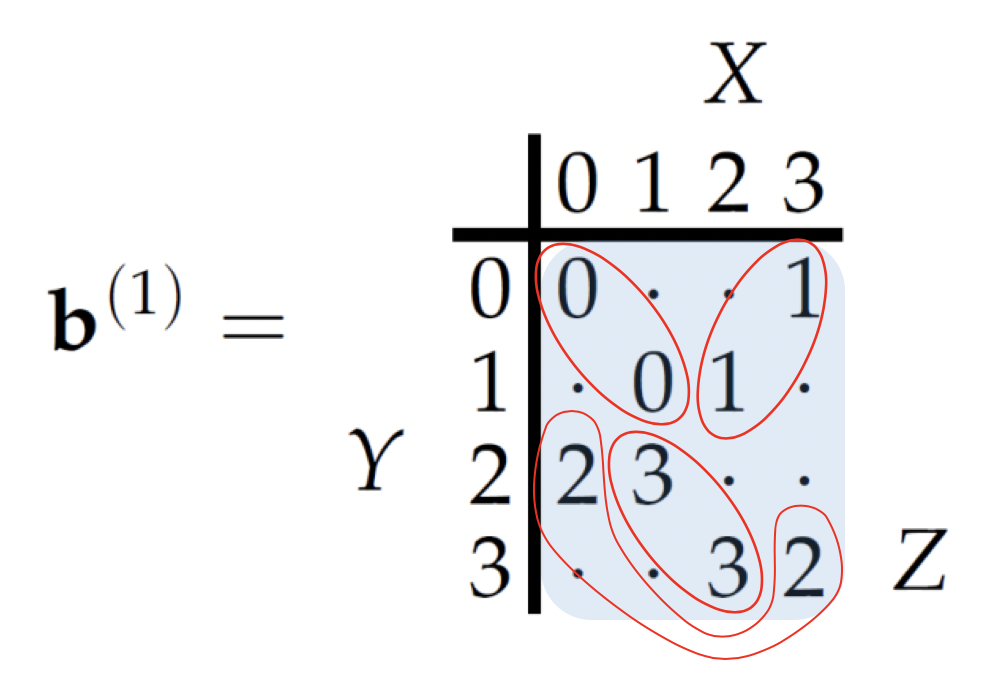
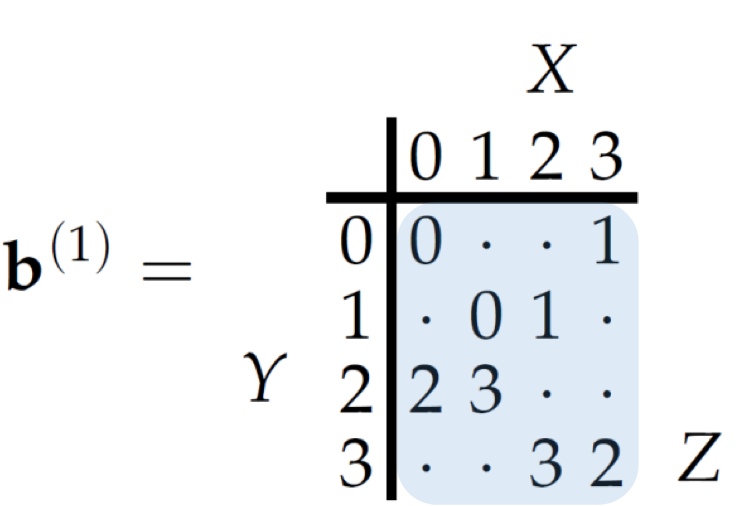
- Bob announces whether \(Y\) belongs to \(\{0,1\}\) or \(\{2,3\}\).
- Eve learns nothing from this announcement.
- Alice knows exactly which \(Y\) Bob has
Construction





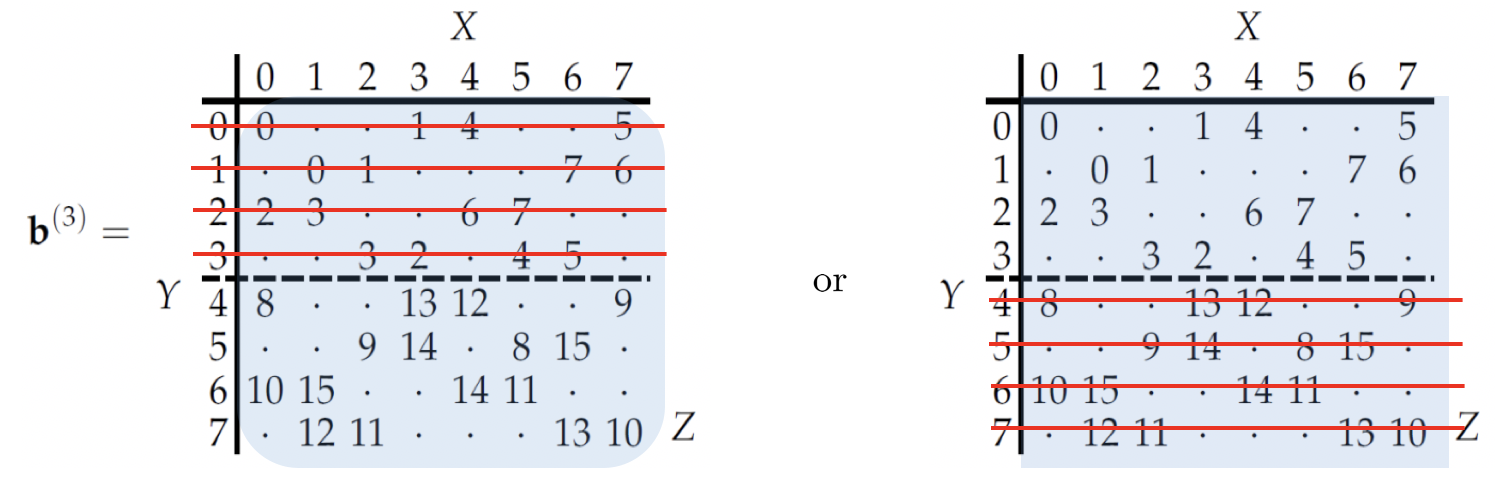
Bob Starts:
