Quantum Resource Theory

Min-Hsiu Hsieh

UTS Centre for Quantum Software and Information

[2] Anurag Anshu, MH, Rahul Jain. Quantifying resource in catalytic resource theory. PRL121:190504 (2018).

[1] Eric Chitambar, MH. Relating the Resource Theories of Entanglement and Quantum Coherence. PRL 117:020402 (2016).

[4] Yu Luo, Yongming Li, MH. Inequivalent Multipartite Coherence Classes and New Coherence Monotones. PRA 99:242306 (2019).

[3] Madhav Krishnan, Eric Chitambar, MH. One-shot assisted concentration of coherence. Journal of Physics A: Mathematical and Theoretical, 51(41):414001 (2018).

[5] Madhav Krishnan, Eric Chitambar, MH. One-shot Distillation in a General Resource Theory. arXiv:1906.04959 (2019).

[6] Hayata Yamasaki, Madhav Krishnan, MH. Hierarchy of quantum operations in manipulating coherence and entanglement. arXiv:1912.11049 (2019).

Resource Theory

(1): Free States

(2): Free Operations

Part I:

How to quantity the amount of resources?

[1] Anurag Anshu, MH, Rahul Jain. Quantifying resource in catalytic resource theory. Accepted in Physical Review Letters. [arXiv:1708.00381].

Main Result:

The amount of resource in \(\rho_M\) is equal to \(E^\infty(\rho_M)\)

E(\rho_M)= \inf_{\sigma_M\in\mathcal{F}} D(\rho_M\|\sigma_M)

It works for

1. Free States form a convex and close set.

2. Free States remain free under tensor product and partial trace.

Concrete Examples

1. Entanglement

2. Coherence

3. Asymmetry

4. Purity

Regularized Relative Entropy of Entanglement is a right measure for the "quantumness".

Resolved an open question in [1].

[1] Groisman, Popescu, and Winter, “Quantum, classical, and total amount of correlations in a quantum state,” Phys. Rev. A, vol. 72, p. 032317, 2005.

Remark

Setup

1. The amount of resource equals the amount of noise used to erase it.

2. Catalyst is allowed.

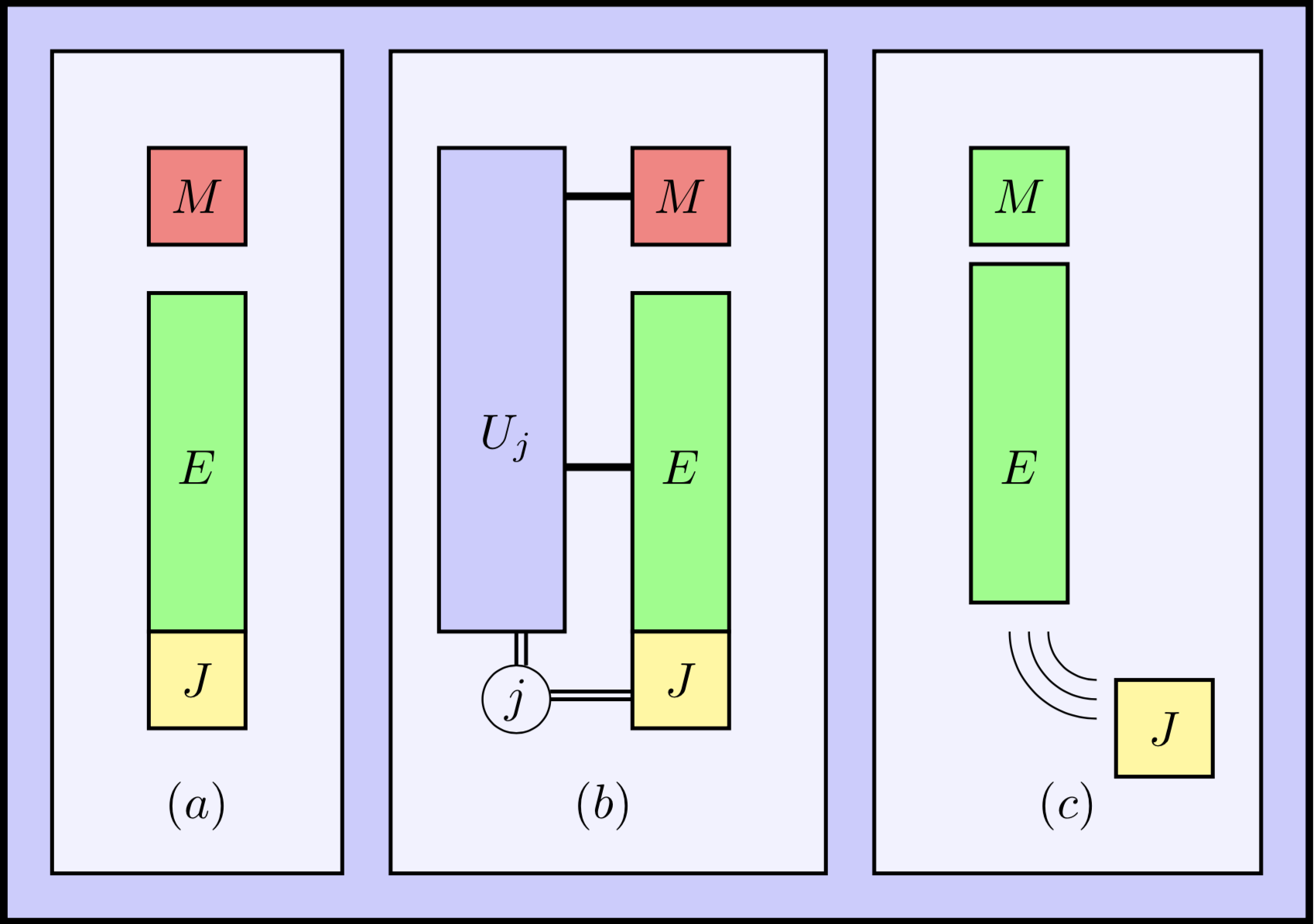
Remark

1. Matching one-shot bounds.

2. Convex Splitting Lemma is used.

Part II:

Interplay of Entanglement and Coherence Resources

[2] Eric Chitambar, MH. Relating the Resource Theories of Entanglement and Quantum Coherence. PRL, vol. 117, p. 020402 (2016).

|\Phi_A\rangle:=\sqrt{1/2}(|0\rangle^A+|1\rangle^A)

|\Phi_{A'B'}\rangle:=\sqrt{1/2}(|00\rangle+|11\rangle)

\mathcal{L}\left(\Phi_A^{\otimes\lceil n(R_A+\epsilon)\rceil}\otimes\Phi_B^{\otimes\lceil n(R_B+\epsilon)\rceil}\otimes\Phi_{A'B'}^{\otimes\lceil n(E^{co}+\epsilon)\rceil}\right)

{\approx}_{\epsilon}\ \ \rho^{\otimes n}

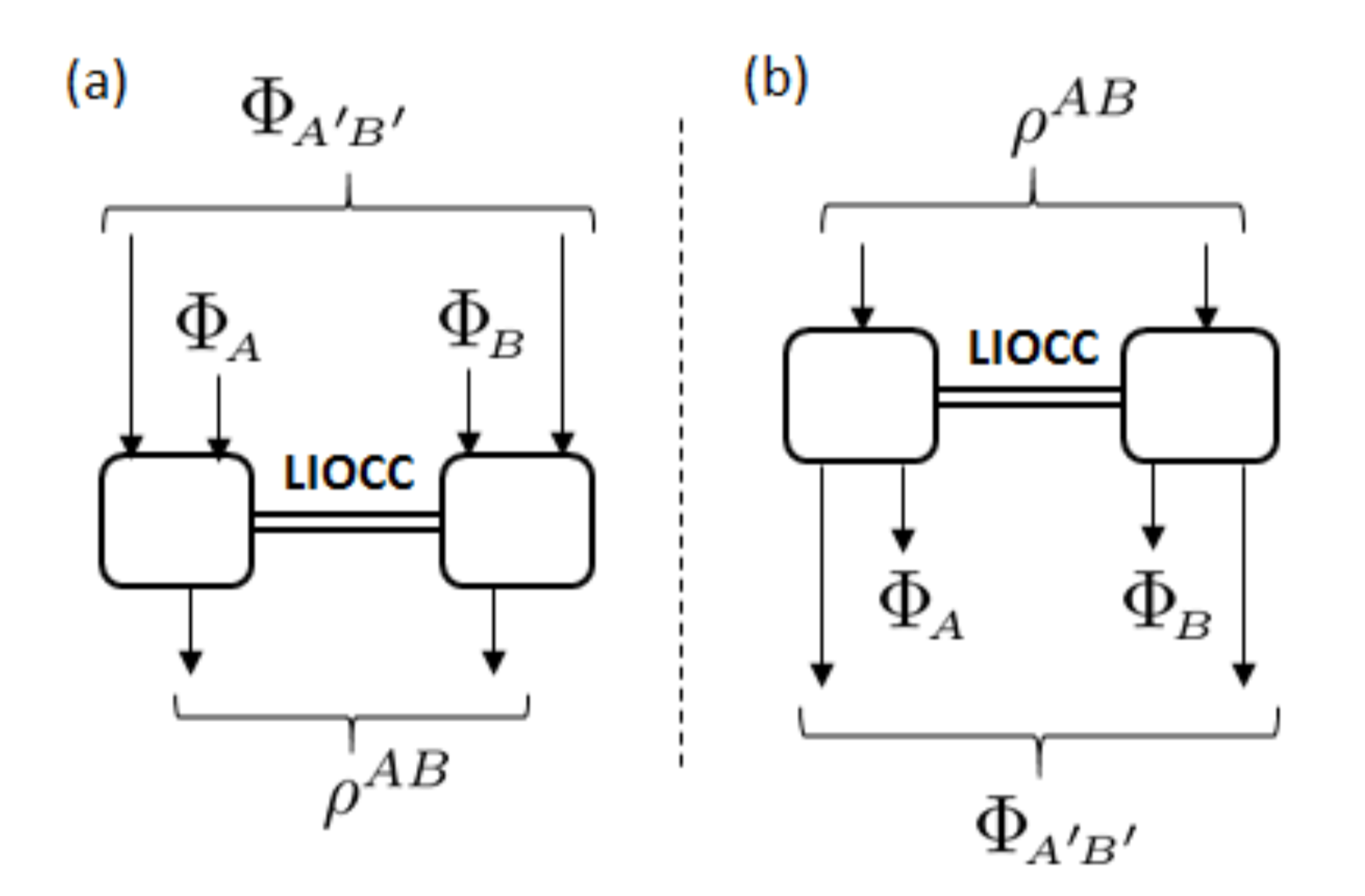
(a) Coherence - Entanglement Formation

What is known...

\mathcal{L}\left(\Phi_A^{\otimes\lceil n(R_A+\epsilon)\rceil}\right)

{\approx}_{\epsilon}\ \ \rho^{\otimes n}

\(R_A\geq S(X)_{\Delta(\Psi_A)}\),

[*]  X. Yuan, H. Zhou, Z. Cao, and X. Ma, Phys. Rev. A 92, 022124 (2015). 

[*]  A. Winter and D. Yang, Phys. Rev. Lett. 116, 120404 (2016).

\geq C_F(\rho)

(i) \(E^{co}\geq \mathrm{E}(\Psi)\),

(ii) \(R_A+R_B\geq S(XY)_{\Delta(\Psi)}\),

(iii) \(R_B+E^{co}\geq S(XY)_{\Delta(\Psi)}\)

Result (a)

For a pure state \(|\Psi_{AB}\rangle\),

Remark

Our result coincides with formation of a mixed state \(\rho\) is given by \(C_F(\rho)\) [1].

[1] A. Winter and D. Yang, Phys. Rev. Lett. 116, 120404 (2016).

However, we need extra \(E^{co}\geq \mathrm{E}(\Psi)\) because of the distributed settings.

Let \(C_M(\Psi):=S(X)_{\Delta(\Psi)}+S(Y)_{\Delta(\Psi)}-{E}(\Psi).\)

\(C_M(\Psi)\) is an LIOCC monotone.

\(C_M(\Psi)=C_a^{A|B}(\Psi)+C_r(\Psi^A).\)

Proof:

Theorem:

\(C_M(\Psi):=S(X)_{\Delta(\Psi)}+S(Y)_{\Delta(\Psi)}-{E}(\Psi).\)

Remark

is an LIOCC monotone, but not an LOCC monotone

(b) Coherence - Entanglement Distillation

\Phi_A^{\otimes\lceil n(R_A-\epsilon)\rceil}\otimes\Phi_B^{\otimes\lceil n(R_B-\epsilon)\rceil}\otimes\Phi_{A'B'}^{\otimes\lceil n(E^{co}-\epsilon)\rceil}

\mathcal{L} (\rho^{\otimes n}) {\approx}_{\epsilon}

What is known...

\mathcal{L} (\rho^{\otimes n}) {\approx}_{\epsilon}

\Phi_A^{\otimes\lceil n(R_A-\epsilon)\rceil}

\(R_A\leq S(X)_{\Delta(\Psi_A)}\),

[*]  A. Winter and D. Yang, Phys. Rev. Lett. 116, 120404 (2016).

Result (b)

For a pure state \(|\Psi_{AB}\rangle\),

(i) \(R_A+R_B\leq C_{M}(\Psi)\)

(ii) \(R_B+E^{co}\leq S(Y)_{\Delta(\Psi)}\)

(iii) \(E^{co} \to \) our paper.

Coherence deficit

\delta(\rho^{AB})=C_D^{Global}(\rho^{AB})-C_D^{LIOCC}(\rho^{AB})

\delta_c(\rho^{AB})=C_D^{LIOCC}(\rho^{AB})-C_D^{LIO}(\rho^{AB})

=\mathrm{E}(\Psi)-I(X:Y)_{\Delta(\Psi)}

=\mathrm{E}(\Psi)

Part III:

Assisted distillation of resources

[3] Madhav Krishnan Vijayan, Eric Chitambar, MH. One-shot assisted concentration of coherence. [arXiv:1804.06554]

[5] Madhav Krishnan, Eric Chitambar, MH. One-shot Distillation in a General Resource Theory. arXiv:1906.04959 (2019).

E_{c}(\psi , \epsilon) := \max_{m \in \mathbb{N}} \left\lbrace m : \right.

\left. \max_{\Lambda \in \mathcal{O}} F^2(\Lambda(\psi), \Phi_{2}^{\otimes m}) \geq 1- \epsilon \right\rbrace

One-Shot Assisted distillation of resource

E_{c}(\psi, \epsilon) \leq \max\limits_{\overline{\psi} \in b_*^{\prime}(\psi, 2\epsilon)} G_{min}(\overline{\psi})

G_{\min}(\rho) = \min_{\gamma \in \mathcal{F}} [ -\log_2 \text{Tr}(\rho \gamma) ]

Theorem

holds

if \(\Phi^n \gamma \Phi^n \leq \frac{1}{2^n}\Phi^n\)

Resource

Theory

Entanglement

Coherence

Purity

G_{\min}(\psi)

S_{\min}(\rho_\psi)

S_{\min}(\Delta(\psi))

\log \dim(\psi)

Part IV:

Multipartite Inequivalent Coherence Classes

[4] Yu Luo, Yongming Li, MH. Inequivalent Multipartite Coherence Classes and New Coherence Monotones. [arXiv:1807.06308].

How many are there for 3-qubit coherence states?

For 3 qubits, there are only two inequivalent entanglement classes under SLOCC.

There are already infinite many inequivalent coherence classes under SLICC for two qubits.

Main Result

# of product

terms

|00\rangle

Classification

a|00\rangle+b|01\rangle

a|00\rangle+b|10\rangle

a|00\rangle+b|11\rangle

a|00\rangle+b|01\rangle+c|10\rangle

a|00\rangle+b|01\rangle+c|11\rangle

a|00\rangle+b|01\rangle+c|10\rangle+d|11\rangle

\Delta= \frac{ad}{bc}

Part V:

Hierarchy of Quantum Operations

[6] Hayata Yamasaki, Madhav Krishnan, MH. Hierarchy of quantum operations in manipulating coherence and entanglement. arXiv:1912.11049 (2019).

\mathcal{E}^{AB}\left(\rho^{AB}\right)\in\mathcal{QI}

\(\mathcal{E}^{AB}\) is QIP iff

\rho^{AB}=\sum_j p\left(j\right)\rho_j^A\otimes{|j\rangle\langle j|}^B

\(\mathcal{E}^{AB}\) is CQIP iff \(\text{id}^{A'B'}\otimes\mathcal{E}^{AB}\) is QIP.

C_{\mathrm{a},\infty}^\textsf{QIP}\left(\psi^{B}\right)=C_{\mathrm{a},\infty}^\textsf{1-LQICC}\left(\psi^{B}\right)=H\left(\Delta\left(\psi^B\right)\right)

\max_{\mathcal{E}\in\mathsf{QIP}}F^2\left(|{\Phi_4}\rangle\langle{\Phi_4}|^B,\mathcal{E}^{AB\to B}\left(|{\psi}\rangle\langle{\psi}|^{AB}\right)\right)=1

\max_{\mathcal{E}\in\mathsf{QIP}\cap\mathsf{PPT}}F^2\left(|{\Phi_4}\rangle\langle{\Phi_4}|^B,\mathcal{E}^{AB\to B}\left(|{\psi}\rangle\langle{\psi}|^{AB}\right)\right)=0.97

Asymptotic

One-Shot

Thank you for your attention!