Machine learning

社課 - 5

lecturer : lemon

topic :

Regularize & Normalize & Initialize

random initialize

感覺很明顯ㄉ

有時候，把初始值設為0並不是一個明智的選擇。

所以我們會隨機選取兩個數字，作為模型的w, b初始值

即Random Initialization

那所以我們就可以回到Numpy的懷抱

接下來

我會簡介一下常用的隨機函式ㄛ

(其實我也只有放兩種

numpy!!!

首先，記得要import numpy欸

Numpy裡提供的random函式，都可以支援矩陣的操作ㄛ

只需要把矩陣維度放在函式裡就可以ㄌ

i.e.

import numpy as np
row = 10 #10列
col = 15 #15行(我應該沒錯ㄅ
#可以像這樣，會產生矩陣
matn = np.random.randn(row, col)
mat = np.random.rand(row, col)
#不放就是只有一個數字ㄛ
singlen = np.random.randn()
single = np.random.rand()

numpy!!!

np.random.rand()

它會回傳[0, 1]之間的隨機數字

也就是類似0% ~ 100%的概念

mat = np.random.rand(10, 20)
print(mat)

numpy!!!

np.random.randn()

它會回傳隨機ㄉ常態分佈

至於這是甚麼意思

好像不太重要 (?

總之就是它會有正有負。

mat = np.random.randn(10, 20)
print(mat)

numpy!!!

我們比較常用的是np.random.randn()

因為它符合常態分布

等等，讓我偷渡一點數學ㄛ

也是可以考慮聽一下啦，反正遲早要學(?

根據常態分布的定義

其平均值\(\mu = 0\)，標準差\(\sigma = 1\)

數學QAQ

如果你(或未來的你)有認真學統計

那麼你會知道：

如果我們有一些資料\(x_1, x_2, ... , x_n\)

其\(\mu = 0, \sigma = 1\)

那麼如果我改變x的值，讓每個x：

\(x^{\prime} = ax + b\)

那麼其\(\mu^{\prime} = b, \sigma^{\prime} = a\)

我們便可以很好的改變函數分布的範圍ㄌ

數學QAQ

我們可以把它寫成程式

你這樣就可以控制隨機的分布ㄌ(茶

a = 10
b = 5
single = a*np.random.randn() + b

ㄛ 沒聽懂也沒關係啦

雖然我等一下會再講一次w

記得認真上統計

reminder

Random Initialize雖然重要

但是在我們目前學到ㄉ

Linear regression, Logistic regression

並不是必要的操作

至於為甚麼要放在這禮拜教

是因為下禮拜東西會有點多w

所以先學感覺會好一點ㄅ

Normalize

Normalize(正規化)

可以有效加快訓練速度和模型準確度

又 又上數學

為了達成這個目的

我們需要讓每個維度的資料(不同feature的資料)

擁有相同的衡量標準

我們通常會讓資料呈現

\(\mu = 0, \sigma = 1\)的分布

Deja vu

根據和前面一樣的手法

我們可以讓：

\(x^{\prime} = \frac{x - \mu_x}{\sigma_x}\)

就會讓\(\mu^{\prime} = 0, \sigma^{\prime} = 1\)

code

一樣，我們把它寫成程式

其中我們會用到

np.mean()(平均)

np.std()(標準差)

有一些重要的參數需要注意：

keepdims = 1：它會維持矩陣的維度，避免出錯

axis = (0/1)： 0(row), 1(col)，它決定合併的維度

這裡補充一下，如果你忘記的話：

\(X \in R^{n \times m}\) 

Code

啊你怎麼長這樣：

X = np.array([[1, 2], 
             [4, 5],
             [7, 8]]) #X is n by m 
#對X的每個col做合併取平均
mu = np.mean(X, axis = 1, keepdims = 1)
#對X的每個col做合併取標準差
sigma = np.std(X, axis = 1, keepdims = 1)
#Normailize
X = (X - mu)/sigma

Reminder

如果在訓練時使用了Normalization

那麼在預測的時候也要先做Normalize

不然東西就廢ㄌ

Regularization

這其實才是最麻煩ㄉ

為了避免Overfitting，Regularization(正則化)很重要

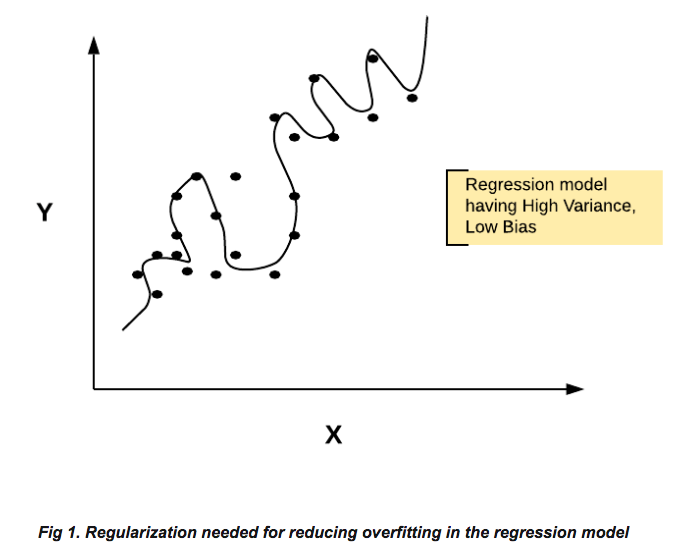
why

有時候我們會考慮在feature中加入另一feature的平方項

比如說\(h = \frac{1}{2}gt^2(g = 10\ m/s^2)\)

我們無法透過簡單的線性關係

\(h = wt + b\)來表示

像這樣的情形

我們會考慮加入一些\(t\)的不同次方項，以求函數的準確度

但這樣的操作，

甚至只要features間，彼此具有某種關係

常常會導致Overfitting的問題

紅玉how

我們可以透過在cost function中多加一項

i.e.(這裡用logistic regression為例)

Z = wX+b, Z \in R^{1 \times m}\\ \\ \hat{y} = \frac{1}{1 + e^{-Z}}, \hat{y} \in R^{1 \times m}\\ \\ J(w, b) = -\frac{1}{m}\sum^{m}_{i = 1}\left [ y^{(i)}*log(\hat{y}^{(i)}) + (1-y^{(i)})*log(1 - \hat{y}^{(i)}) \right ] +\\ \frac{\lambda}{2m}\sum^{n}_{i = 1} w_{j}^{2}

讓權重的大小也成為Cost的來源

gradient

\frac{\partial J}{\partial w} = \frac{1}{m}(\hat{y} - y)\times X^{T} + \frac{\lambda}{m} w\\\\ \frac{\partial J}{\partial b} = \frac{1}{m}\sum^{m}_{i=1}(\hat{y}^{(i)} - y^{(i)})\\\\ w \coloneqq w - \alpha \frac{\partial J}{\partial w}\\\\ b \coloneqq b - \alpha \frac{\partial J}{\partial b}

就只是在後面多加一項而已ㄛ

lambda

透過改變\(\lambda\)的值，

我們可以改變Regularize的程度

underfitting

你的模型爛掉ㄌ QAQ

reminder

\(\lambda\)需要手動的調整，

程式練習時可以自己試試看，

不同的\(\lambda\)會對模型產生甚麼影響，

btw每個模型所需要的\(\lambda\)可能不同。

 

反正就試試看ㄅ

image processing

我們要把它reshape

code

X = np.array([[1, 2], 
             [4, 5],
             [7, 8]]) #X is 3 by 2
#now X is 1 by 6
X = X.reshape((1, 6))

.reshape()會回傳改變形狀後的結果

colab

這禮拜我比較有空w

所以Colab應該是做得相當認真ㄉ

有問題都可以問ㄛ

btw下個禮拜的東西可能比較難

但是真的很酷

記得要來ㄛ

答案

\學弟妹來秋遊/

雖然好像截止ㄌ

來陪我吃肉肉

大概就這樣

下次也要來ㄛ

Made with Slides.com