Learning Features in Neural Nets:
perks and drawbacks
Candidacy Exam
Candidate: Leonardo Petrini
Exam jury:
President: Dr. Marcia T. Portella Oberli
Expert: Prof. Lenka Zdeborova
Thesis advisor: Prof. Matthieu Wyart

October 27, 2020
Neural Networks | in a nutshell
Neural nets are a \(-\) biologically inspired and incredibly effective \(-\) way of parametrizing the function \(f_\theta(\mathbf x)\):
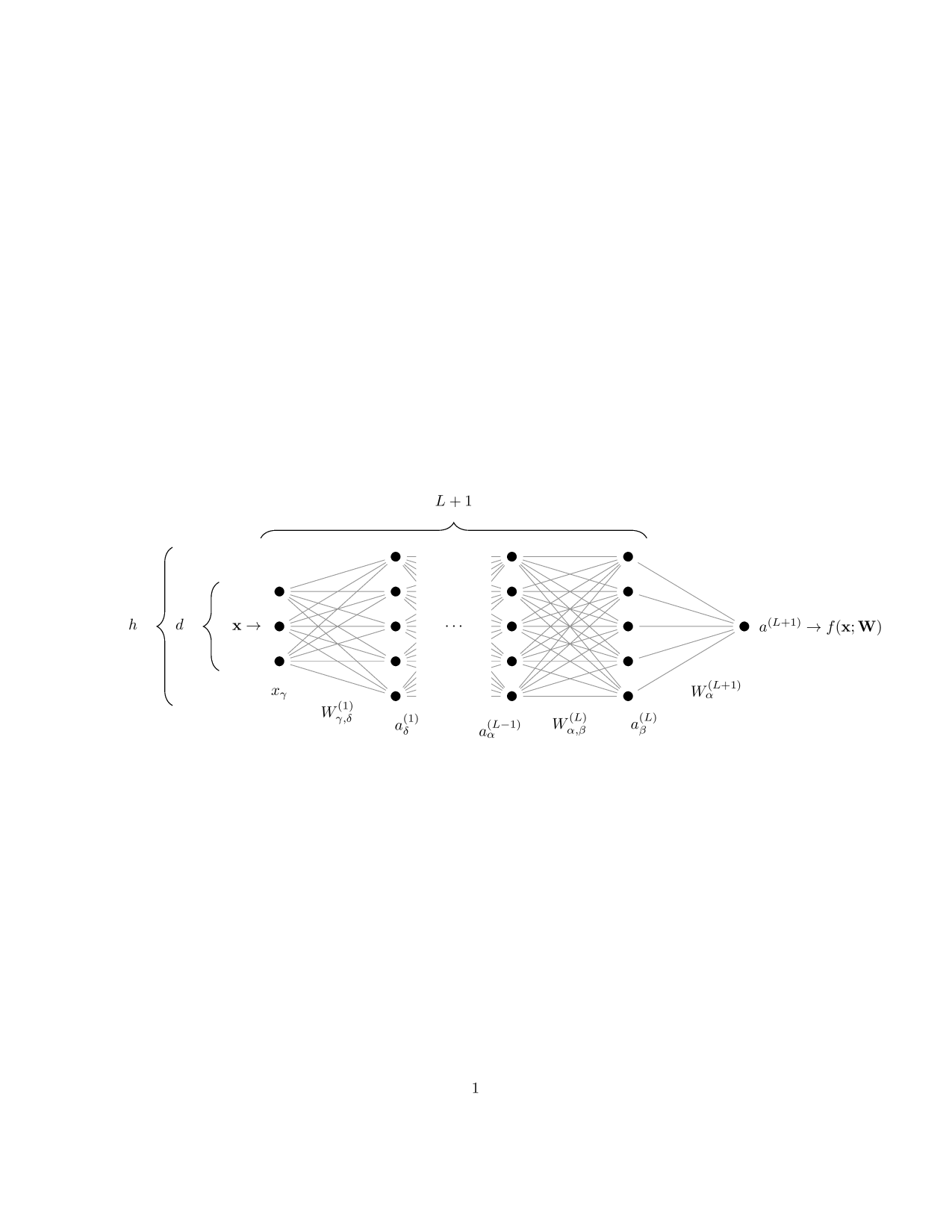
Setting: we have some data observations \(\{\mathbf x^\mu, y^\mu\}_{\mu = 1}^p\) and we suppose there exists an underlying true function \(f^*\) that generated them:
$$y^\mu = f^*(\mathbf x^\mu) + \text{noise}$$
Goal (supervised-learning): find a parametrized function \(f_\theta\) that can properly approximate \(f^*\) and tune the parameters \(\theta\) in order to do so.
Adapted from Geiger et al. (2018)
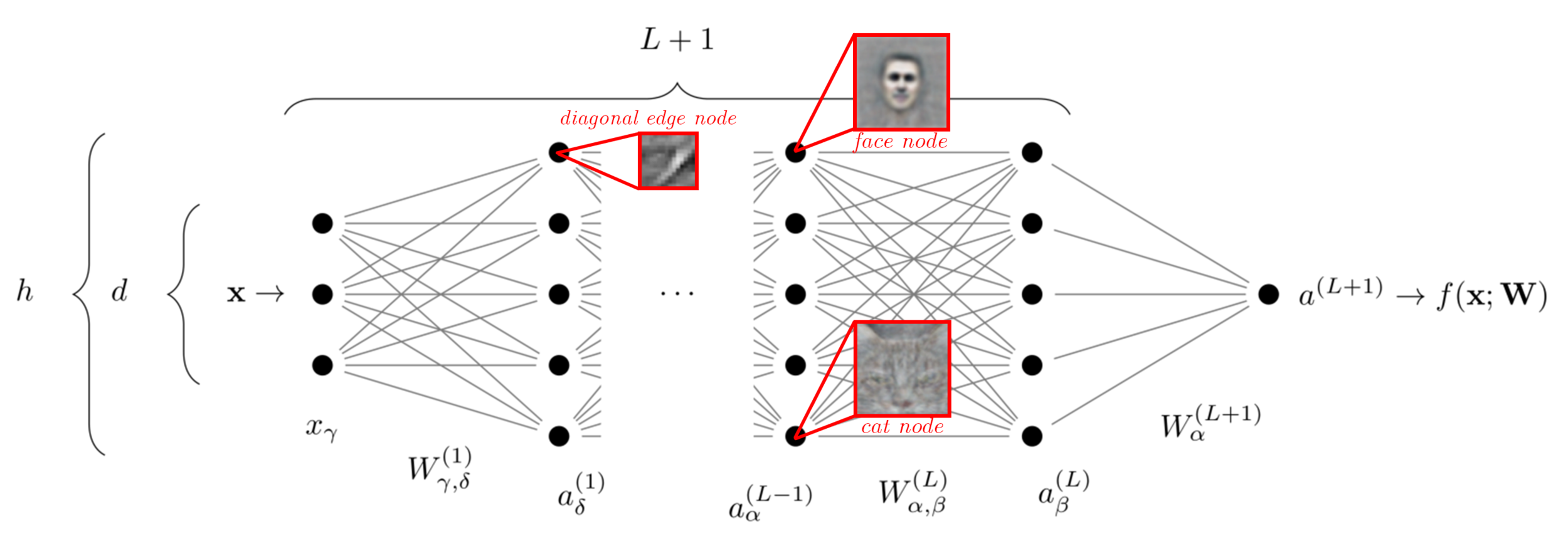
Motivation
The success of neural nets is often attributed to their ability to
-
Learn relevant features of the data
- Become invariant to irrelevant features (compression)
[Mallat (2016)]

e.g. pixels in the corner are unrelated to the class label
CIFAR10 data-point

or even the
background color
Compression in Neural Nets
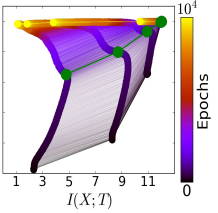
(1) Information-theoretical point of view:
- First, the network function \(f_\theta(\mathbf x)\) gets informative about both the inputs \(\mathbf x^\mu\) and the labels \(y^\mu\) \(-\) both \(I(f_\theta(\mathbf x); \mathbf x)\) and \(I(f_\theta(\mathbf x); y)\) grow.
- Then, \(f_\theta(\mathbf x)\) compresses its representation of the input, getting rid of irrelevant information \(-\) \(I(f_\theta(\mathbf x); \mathbf x)\) decreases.
- However, Saxe et al. (2018) uncovered some serious flaws of this approach.
[Shwartz-Ziv and Tishby (2017)]
[Ansuini et al. (2019),
Recanatesi et al. (2019)]
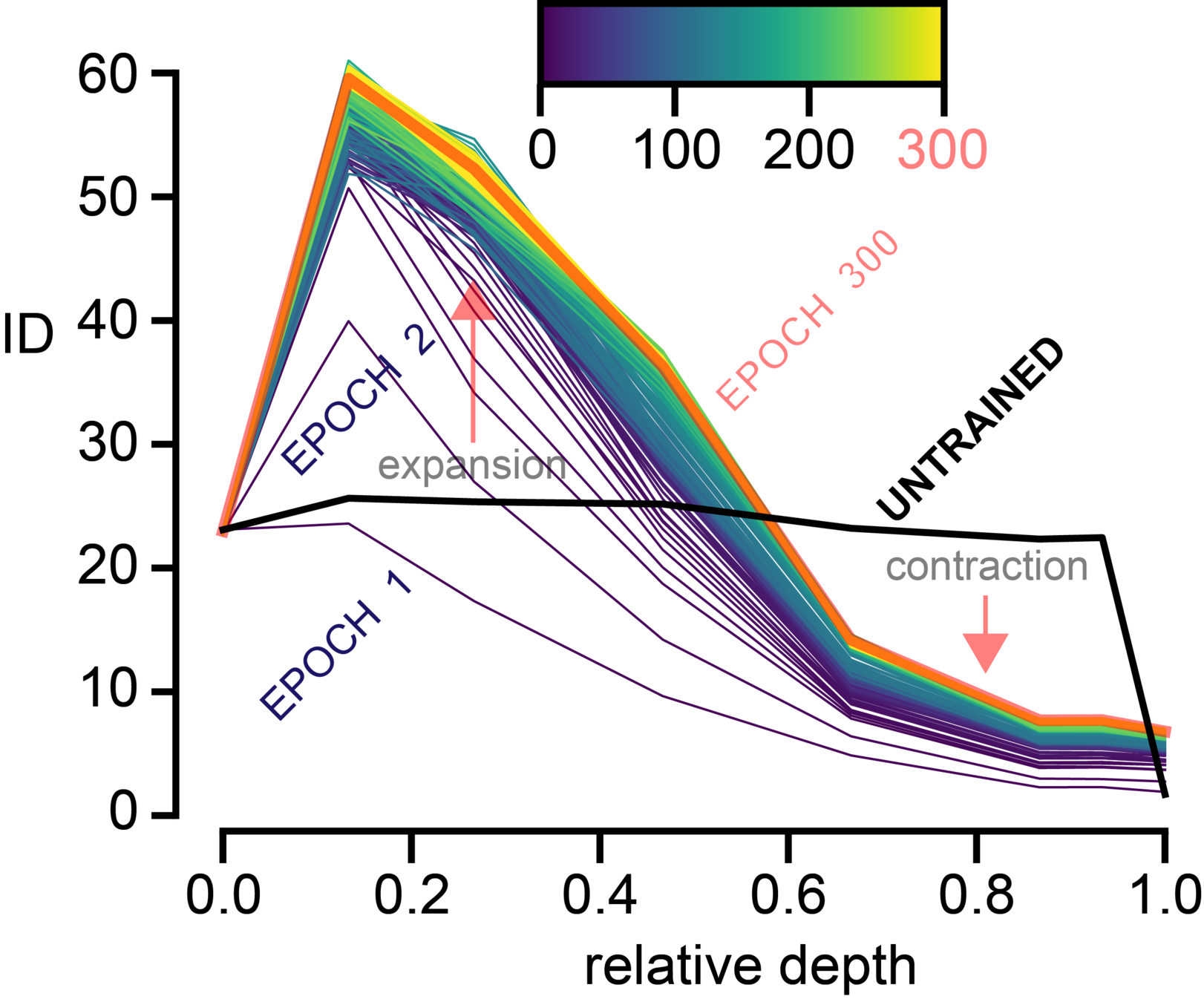
(2) "Geometrical" point of view:
- The intrinsic dimension (ID) progressively reduces
with depth, for deep layers.
ID can be thought of as the number of
variables needed in a minimal
representation of the data.
- Some directions in space are compressed by the network during learning.

example
Neural Nets Learning Regimes
starting from [Jacot et al. 2018]...
Lazy Regime
Feature Regime
-
[weigths space] the net function only moves on a tangent space:
\(f(\theta) \approx f(\theta_0) + \nabla_\theta f(\theta_0)\cdot d \theta\)
-
weights are approximately constant during learning
- Cannot learn features of the data
\(t\): training time
-
[weights space] the net function moves significantly
-
weights evolve during learning
- Can possibly learn features and perform compression!!
tangent space
tangent space
Neural Nets Learning Regimes | NTK
Lazy Regime
Feature Regime
- Evolution of \(f\) is bound to the tangent space \(\rightarrow\) the NTK is constant during learning
- Network dynamics equivalent to a Kernel method
Jacot et al. (2018): to each net we can associate a kernel, the Neural Tangent Kernel (NTK):

\(t\): training time
tangent space
- The NTK evolves during learning
- Can we employ the evolving NTK as an observable?

tangent space
NTK dynamics
\(\dot \theta = -\nabla_\theta \mathcal{L}\)
Gradient Flow
(weights space)
NTK:
Gradient Flow
in function space
}
NTK
Learning Regimes & Performance
How does operating in the feature or lazy regime affect deep nets performance?
Each regime can be favoured by different architectures and data structures [Geiger et al. 2019]:
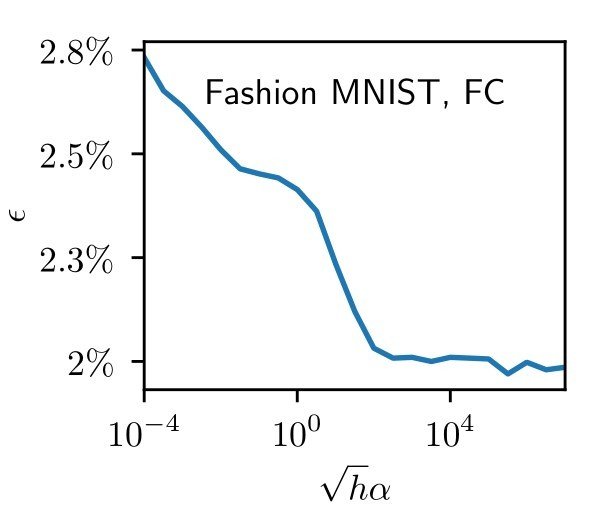
Test error
feature lazy
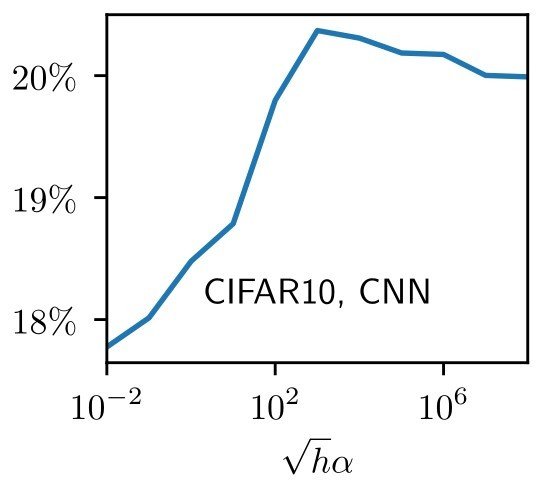
Test error
feature lazy
MNIST, CNN
\(\epsilon_t\)
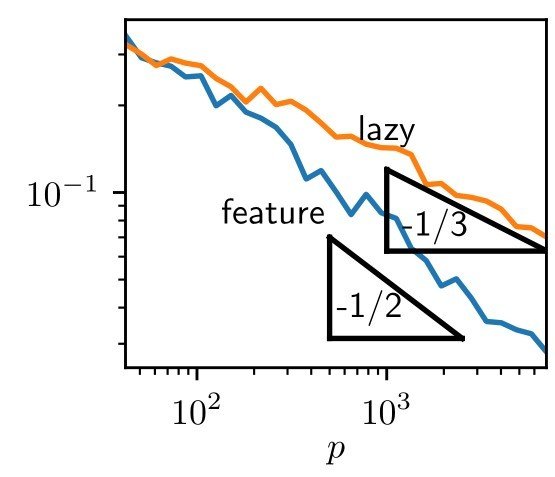
Moreover, if we look at learning curves:
we measure a different exponent \(\beta\) for the two regimes.
In the following, we will use \(\beta\) to characterize performance.
test error
train. set size



To sum up:
- The feature regime seems to be relevant in state of the art architectures and real data
- Yet, it is not always favorable \(-\) for a neural net \(-\) to operate in this regime.
Some questions arise:
- What are the benefits and drawbacks of the feature regime?
- Can we design models (for data and architectures) which reproduce real data observations while allowing to isolate these benefits and drawbacks, in order to better study and characterize them?


Outline | Current Work on Feature Learning
Part II | the drawbacks:
Part I | the perks:
- A model for compression \(-\) the stripe model
- Training dynamics
- Neural Tangent Kernel as observable | Kernel PCA
- Measuring performance | Learning Curves
- Empirical data | MNIST
- The intrinsic dimension of network representation
- No compression needed \(-\) the sphere model
- Neurons dynamics
- The Role of Attractors
- Attractors in real data?
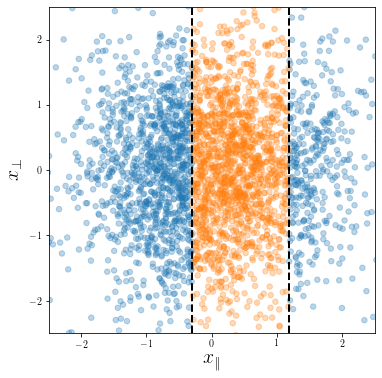
Fully connected one-hidden layer NN:
$$f(\mathbf x) = \frac{1}{h} \sum_{n=1}^h \beta_n \: \sigma \left(\frac{\mathbf{\omega}_n \cdot \mathbf x}{\sqrt{d}} + b_n \right)$$
\(\mathbf x^\mu \sim \mathcal{N}(0, I_d)\), for \(\mu=1,\dots,p\)
Classification task: \(y(\mathbf x) = y( x_\parallel) \in \{-1, 1\}\)
Simple model for compression |
The Stripe Model
Dataset
Architecture
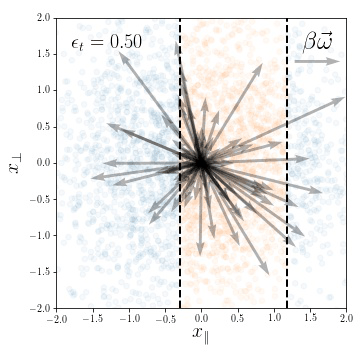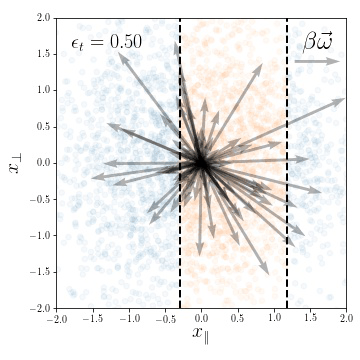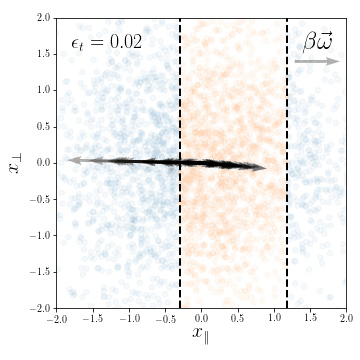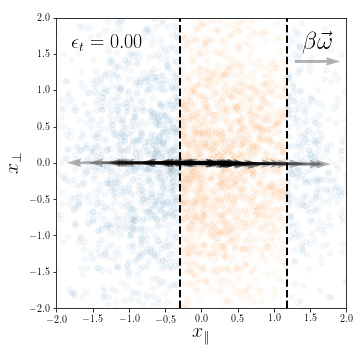
weights evolution during training
for a subset of neurons

Training Dynamics
Compression in the feature regime

weights evolution during training
for a subset of neurons

Compression and the Neural Tangent Kernel:
- The network function loses its dependence on the \(x_\bot\) direction
- NTK evolves with weights and also loses dependence on \(x_\bot\)
more formal argument in the preprint arXiv:2007.11471 - NTK eigenvectors are of two kinds:
\(\phi^1_\lambda(\vec x)= \phi_\lambda^1(\vec x_\parallel)\) and \(\phi^2_\lambda(\vec x) = \phi_\lambda^2(\vec x_\parallel) \vec u \cdot \vec x_\bot\) - Given that the labelling function \(y(\vec x) = y(x_\parallel)\), we expect \(\phi_\lambda(\vec x)\) at the end of training to be informative about the label
- We also expect top \(\phi_\lambda(\vec x)\) projection on the label to be large
- For kernel methods, if this projection on top eigenvectors is large, one expects good performance [Schölkopf et al. 2002]
Training Dynamics
Compression in the feature regime
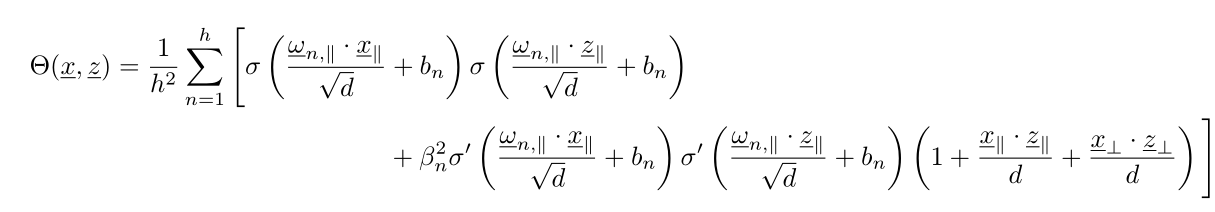
one-hidden layer fully connected NTK after compressing \(\mathbf x_\bot\)
Alignment between kernel eigenvectors and labelling function determines performance (some intuition):
The ideal kernel for a classification target \(y(x)\) would be \(K^*(x, z) = y(x)y(z)\).
A kernel is more performant on a classification target \(y(x)\) the larger is its alignment with the ideal kernel. That is, the larger the overlap between its eigenvectors and \(y(x)\)
- Top kernel principal components more informative on output label
- Larger projection \(\rightarrow\) expect improved end-of-training NTK performance (if used in a kernel method)
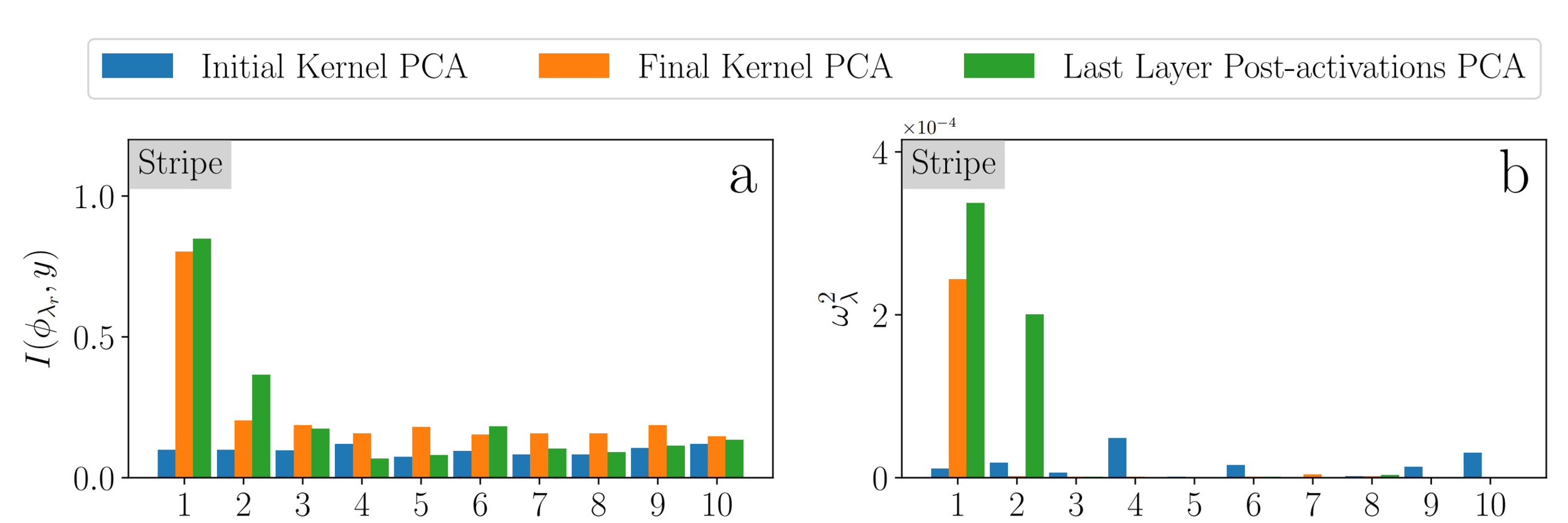
Mutual Information
Projection
Testing predictions via Kernel PCA
- Net in the Lazy Regime
- Net in the Feature Regime
- Kernel Dynamics with NTK after training
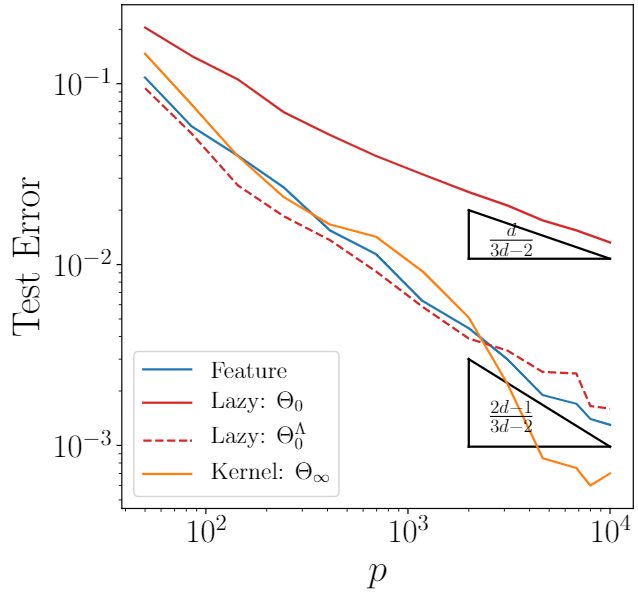
(training set size)
The kernel at the end of learning performs as good as the network itself!
Compression makes the NTK more performant!
Measuring Performance | Learning Curves
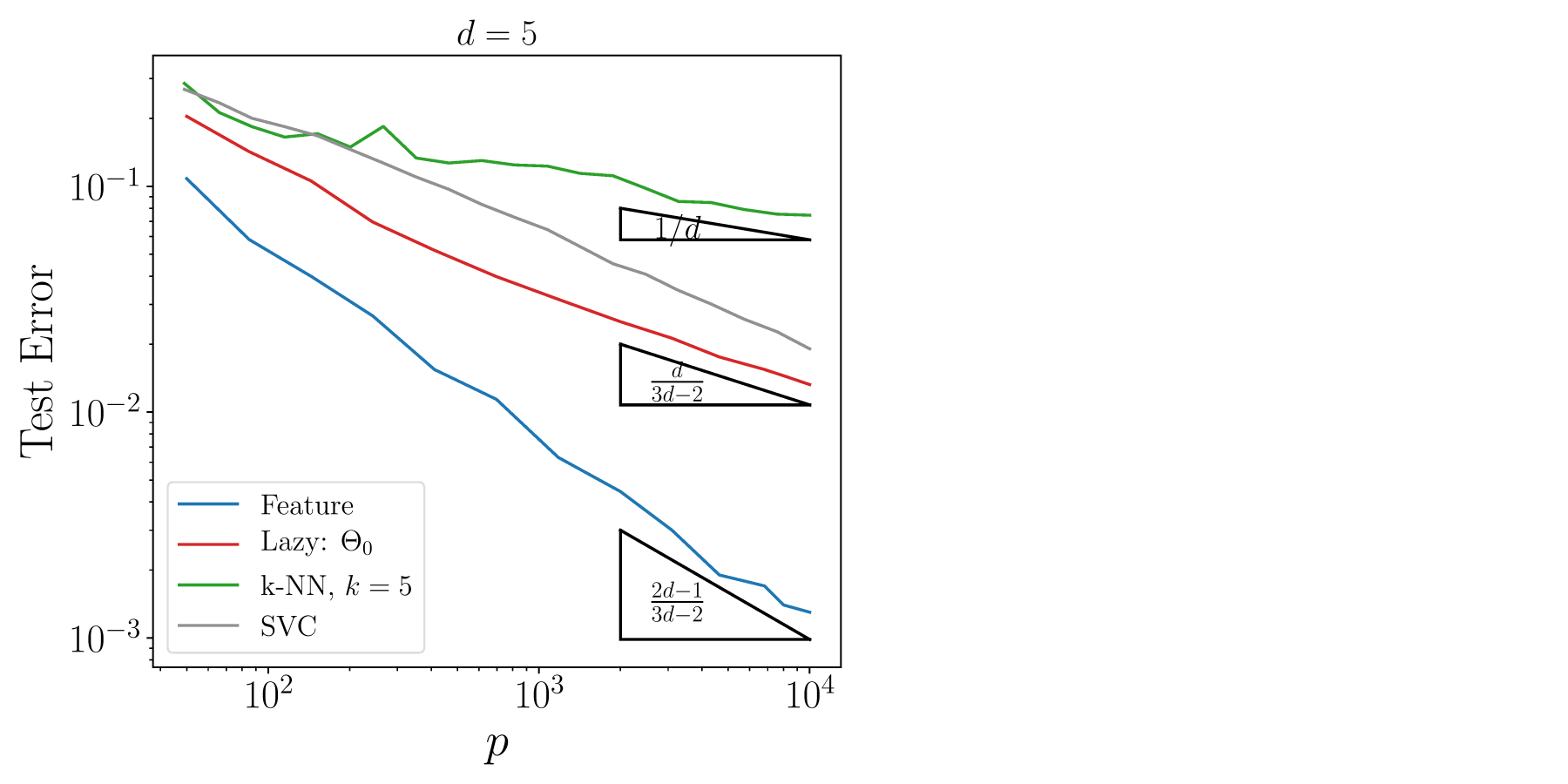
- Net in the Feature Regime
- Net in the Lazy Regime
- Support Vector Classifier (SVC) with NTK at initialization
- k-Nearest Neighbors Algorithm with \(k=5\)
Measuring Performance | Learning Curves
classes interface
o
Support
vectors
SVs distance suffers the curse of dimensionality but, if the interface is regular enough between two SVs, the curse does not affect kernel performance.
This is only true for classification.
[Paccolat et al. (2020)]

Mutual Information
Projection
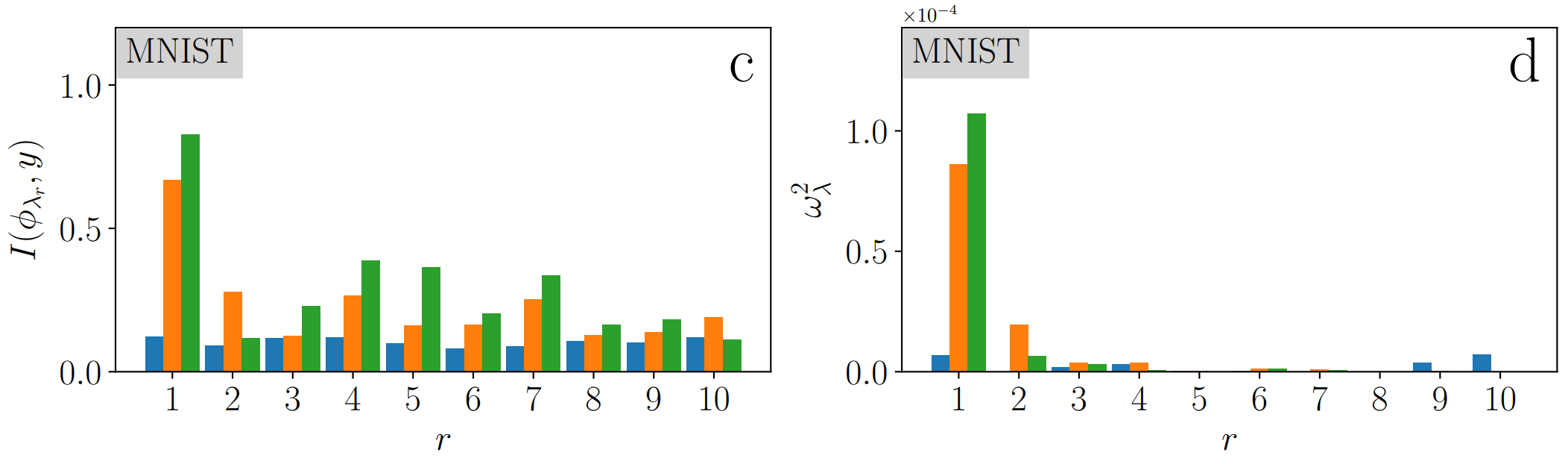
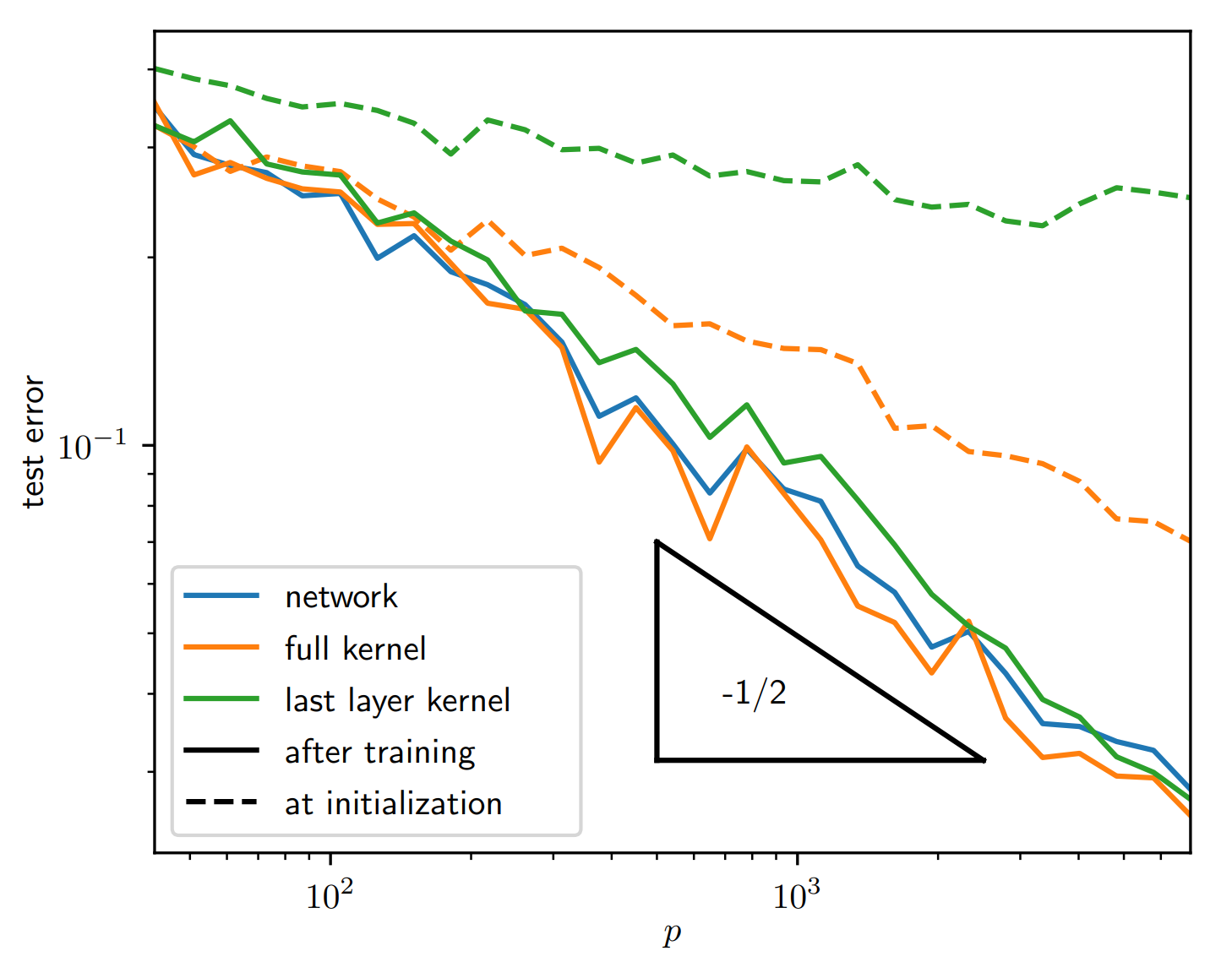
Learning Curves
Similarities with Stripe Model
→ hint to compression being key also in MNIST
Empirical Data | MNIST

...
[Ansuini et al. (2019)]

Intrinsic Dimension | Last hidden-layer
- Recall: compression is expected to occur in the last layers of a network.
- In the Stripe Model, hidden neurons activity can only depend on a single variable, \(x_\parallel\).
- We can look at last-layer manifold by projecting it onto its first two principal components:
Such a dimension-reduction to a ~1D manifold clearly appears in MNIST as well
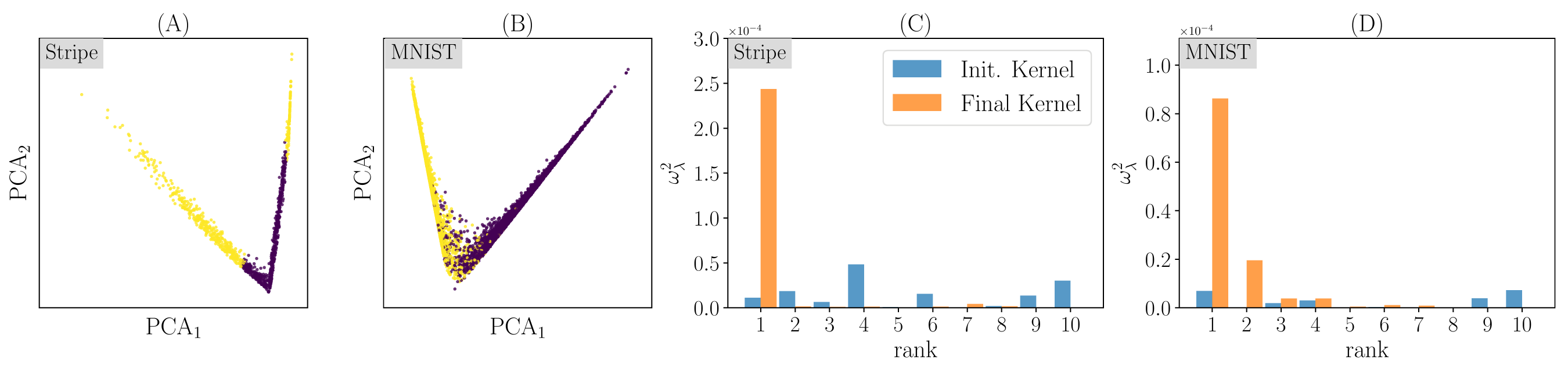

Last hidden-layer pre-activations PCA
color: class label
Outline | Current Work on Feature Learning
Part II | the drawbacks:
Part I | the perks:
- A model for compression \(-\) the stripe model
- Training dynamics
- Neural Tangent Kernel as observable | Kernel PCA
- Measuring performance | Learning Curves
- Empirical data | MNIST
- The intrinsic dimension of network representation
- No compression needed \(-\) the sphere model
- Neurons dynamics
- The Role of Attractors
- Attractors in real data?
[...]

No compression needed |
The Sphere Model
\(\mathbf x^\mu \sim \mathcal{N}(0, I_d)\), for \(\mu=1,\dots,p\)
Classification task is rotationally invariant:
\(y(\mathbf x) = y(||\mathbf {x}||) \in \{-1, 1\}\)

No compression needed |
The Sphere Model
- The symmetry of the task leaves no space for compression
- The initial distribution of the weights respects the task symmetry
- The lazy regime does not change weights orientation \(\rightarrow\) good prior on the task
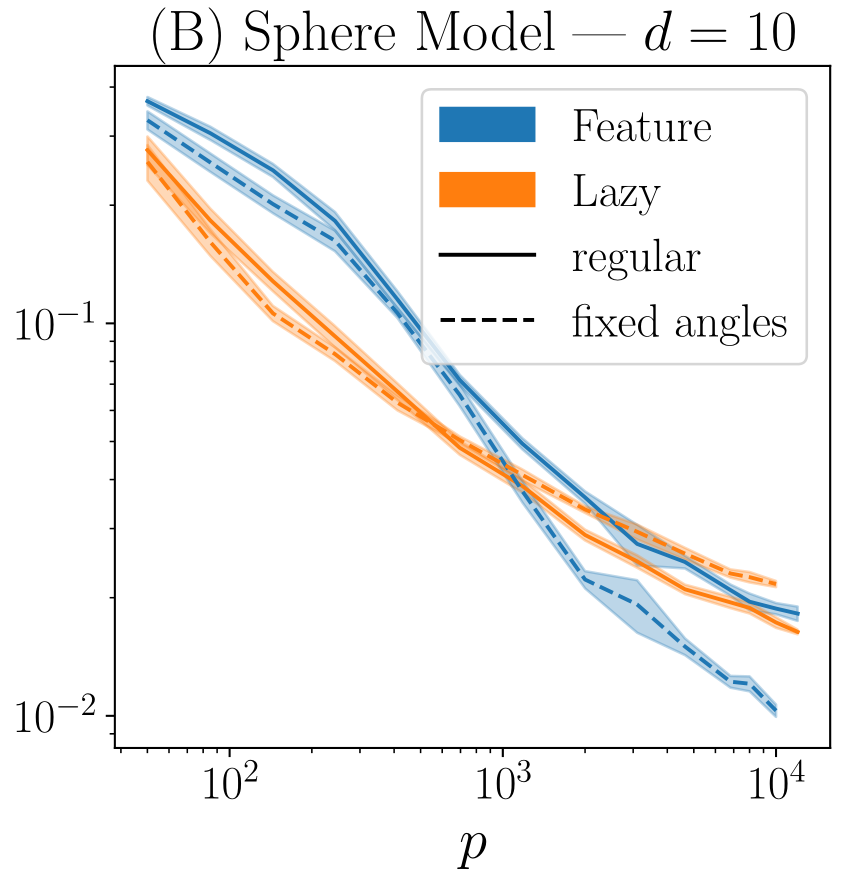
Learning curves | \(d=10\)
- Indeed, there is a \(p^*\) under which lazy > feature
- For small \(p\) (or large \(d\)), fluctuations in the data are large and feature \(-\) by orienting weights \(-\)over-fits them
- In fact, if we fix weights orientation, feature performance improves (dashed curves)
Neurons Dynamics |
- In this context, we need to track neurons evolution more carefully.
- Recall: $$f(\mathbf x) = \frac{1}{h} \sum_{n=1}^h \beta_n \: \sigma \left(\frac{\mathbf{\omega}_n \cdot \mathbf x}{\sqrt{d}} + b_n \right),$$ with \(\sigma(\cdot) = \text{ReLU}(\cdot) = \max(0, \cdot\,)\).
- We can characterize each neuron \(n\) with the point \(-\) nearest to the origin \(-\) at which the argument of the ReLU changes sign. This is
- \(\rightarrow\) follow the neurons evolution in time, in input space
\(0\)
e.g. in 1D:
ReLU
\(\mathbf z\)
\(\mathbf x\)

neurons
Neurons Dynamics |
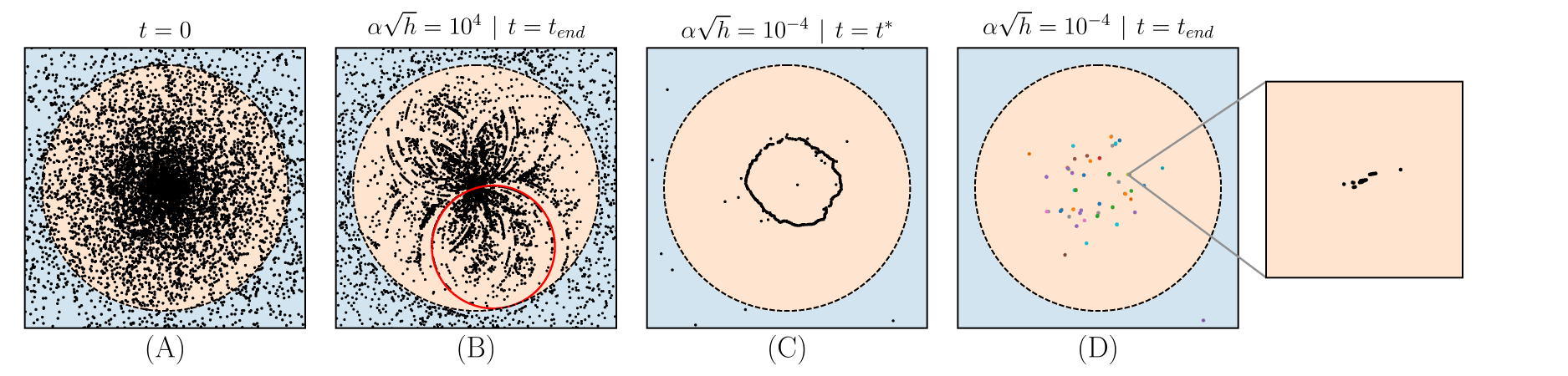
\(0\)
in 1D:
ReLU
\(\mathbf z\)
\(\mathbf x\)
Distribution of \(\mathbf z\) for:
(A) Initialization
(B) Lazy | end of train.
(C) Feature| during tr.
(D) Feature| end of tr.
- (A) At t = 0, the distribution of \(\mathbf z\) reflects the Gaussian initialization of the weights.
- (B) Toward lazy, neurons motion is limited, yet they organize into a flower pattern \(-\) intersection of circles in fact.
- (C) In the feature regime, the neurons move and organize into a circular structure at intermediary times \(-\) task symmetry is preserved.
- (D) At the end of training, the circle explodes into a finite number of attractors \(-\) task symmetry is broken.
The role of Attractors | Work in progress...
Def. an attractor is a set of neurons that are active on the same subset of training points.

here neurons are grouped together by color, following the attractor definition
Gradient flow dynamics:
$$\dot W = -\nabla_W \mathcal{L}$$
where \(W\) can be any of the net weights \(\omega_n\), \(b_n\), \(\beta_n\).
Recall:
One can derive
the direction of this ineq. depending on the sign of \(b\)
Notice: such an attractor can be replaced by a single neuron without affecting \(f(\mathbf x)\) on the training set.
Short-term goals:
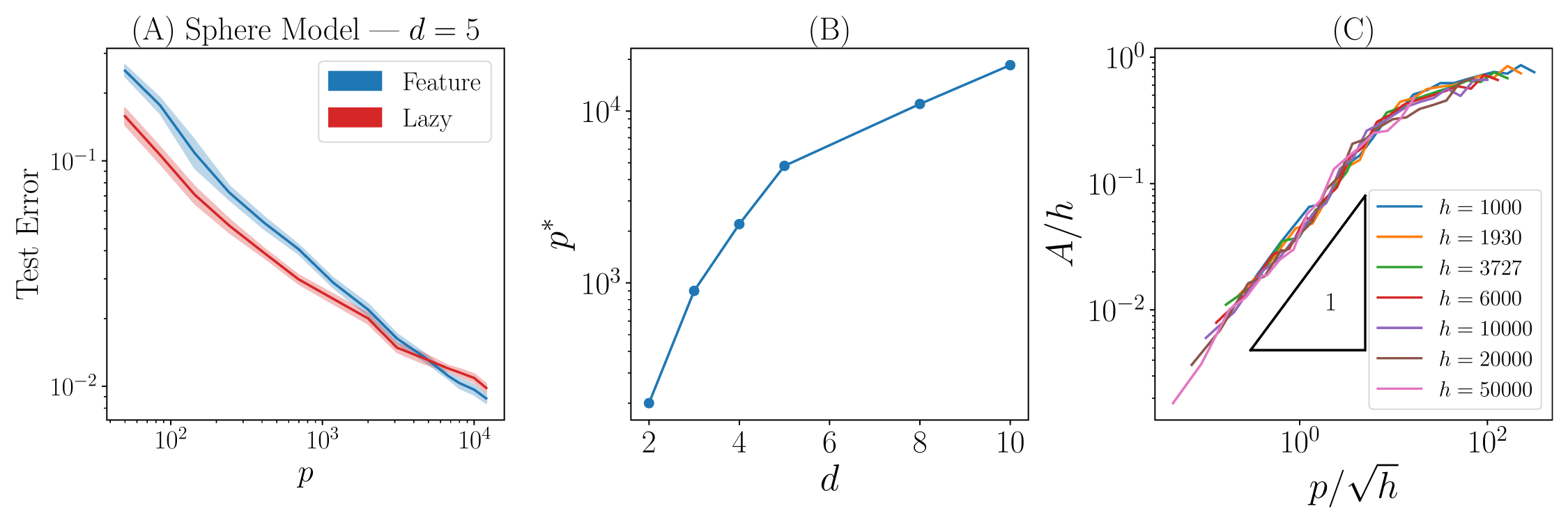
- Understanding how the number of attractors \(A\) depends on \(p\), \(h\) and \(d\). Some preliminary results suggest \(A \sim p\sqrt{h}\) until they reach the saturation at \(A \sim h\):
- Uncover the mechanism leading to attractors formation during the dynamics by studying the fixed points of $$\dot{\mathbf z} = F(\mathbf z)$$

The role of Attractors | Work in progress...
Field \(\dot{\mathbf z}\) for \(p=1\)
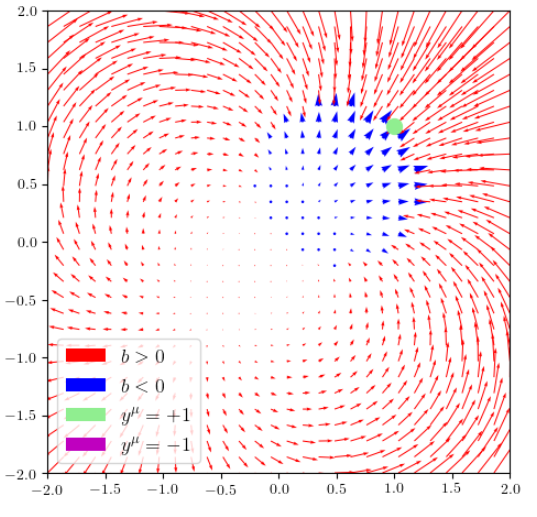
The role of Attractors | Work in progress...
- In the sphere model, the appearance of attractors penalizes performance because the symmetry of the problem is such that a continuous density of neurons is required.
What's the case for real data?
- As an example, for a fully-connected net trained on 10-PCA MNIST we observe the same kind of sparsification in \(\mathbf z\) space.
- Sparsification - in this case - does not seem to be detrimental (feature > lazy).
Research Goal: extend the study of attractors to other simple models in order to understand how they affect performance and bridge the gap with observations in real data.
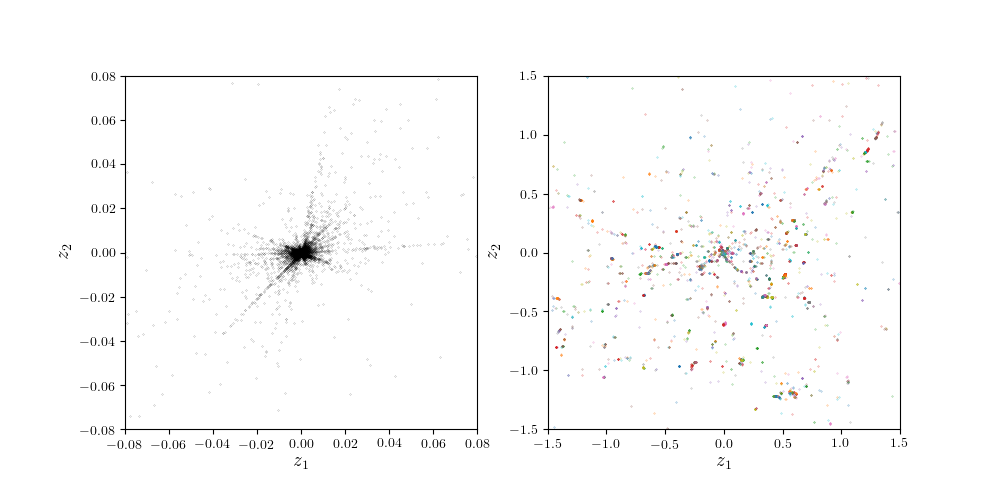
10-PCA MNIST | end of train. neurons position
From Results to Future Work
- Introduced a simple model for compression of invariants in the feature regime
- NTK as an observable with the use of Kernel-PCA
-
Similarities Stripe-MNIST \(\rightarrow\) compression is relevant in both
- Introduced a simple model where compression has no role and feature over-fits by breaking the symmetry, degrading performance
- An infinitely wide net acts as a finite number of neurons \(-\) which form attractors
- How do attractors form dynamically?
- How do they depend on the model parameters?
- What role such attractors play in real settings?
thank you!
Long-term:
- Extend this approach to minimal CNN models exploiting both translational invariance and locality
- Introduce new data models \(-\) eventually hierarchical for multi-layer CNNs