Relative stability toward diffeomorphisms indicates performance in deep nets

Leonardo Petrini, Alessandro Favero, Mario Geiger, Matthieu Wyart

spoc+idephics+pcsl group meeting

May 17, 2021

arXiv:2105.02468

Introduction

Motivation: the success of deep learning (i)

Deep learning is incredibly successful in wide variety of tasks

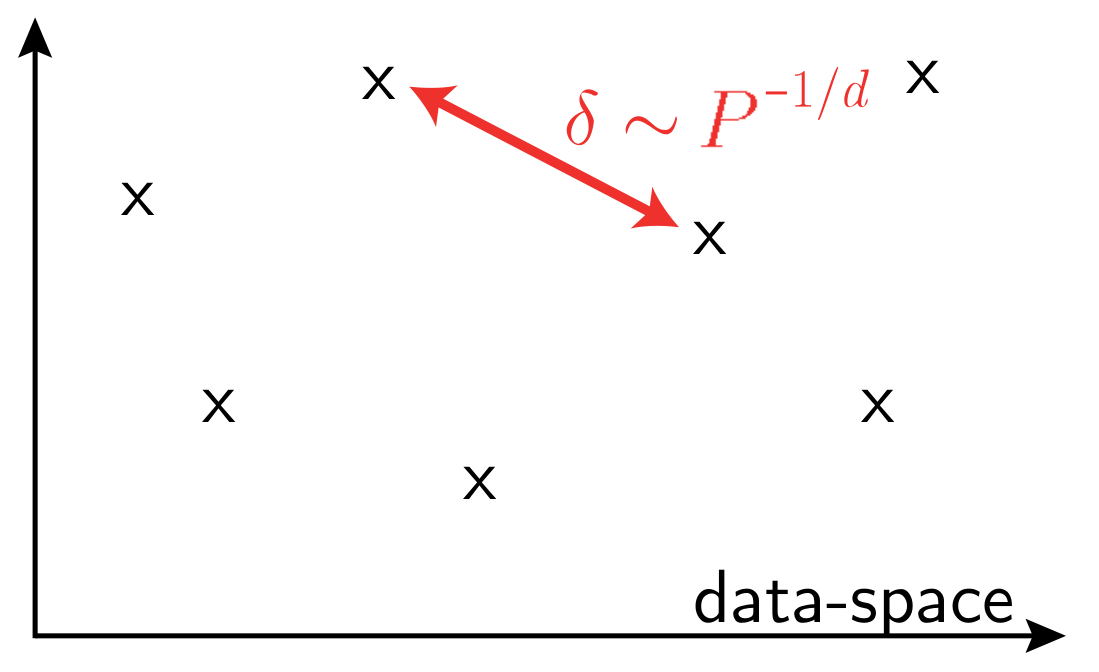
Curse of dimensionality when learning in high-dimension,
in a generic setting

vs.

Learning in high-d implies that data is highly structured

$P$: training set size

$d$ data-space dimension

cats

dogs

embedding space: 3D

data manifold: 2D

task: 1D

Common idea: nets can exploit data structure by getting
invariant to some aspects of the data.

Observables:

Mutual information: NNs get rid of irrelevant information about the input
Intrinsic dimension: dimensionality of NNs representation is reduced with training and depth.
Nets' kernels PCA: the eigenvectors responsible for most of the variance have large projection on the labels (after training)

Motivation: the success of deep learning (ii)

Which invariances are learnt by neural nets?

not explaining:

Some insights from the theory of shallow nets...

Shwartz-Ziv and Tishby (2017); Saxe et al. (2019)

Ansuini et al. (2019), Recanatesi et al. (2019)

Kopitkov and Indelman (2020); Oymak et al. (2019);
Paccolat et al. (2020)

Theory of over-parametrized fully connected (FC) nets:
two training regimes exist, depending on the initialization scale

feature learning

(rich, hydrodynamic...)

neural representation evolves

Learning features in neural nets

lazy training

$\sim$ kernel method

vs.

Performance:

Feature > lazy if FC and task is highly anisotropic
(i.e. it only depends on a linear subspace of input space)
Yet, lazy > feature for FC on real data
$\rightarrow$ learning linear invariance is not relevant here
and feature > lazy for CNNs on real data

Jacot et al. (2018); Chizat et al. (2019); Bach (2018); Mei et al. (2018); Rotskoff and Vanden-Eijnden (2018)...

Bach (2017);
Chizat and Bach (2020); Ghorbani et al. (2019, 2020); Paccolat et al. (2020);
Refinetti et al. (2021);
Yehudai and Shamir (2019)...

Geiger et al. (2020a,b); Lee et al. (2020)

Which data invariances are CNNs learning?

x_\parallel

x_\bot

e.g.

CIFAR10 data-point

Hypothesis: images can be classified because the task is invariant to smooth deformations of small magnitude and CNNs exploit such invariance with training.

Invariance toward diffeomorphisms

Bruna and Mallat (2013) Mallat (2016)

...

Is it true or not?

Can we test it?

"Hypothesis" means, informally:

$\|f(x) - f(\tau x)\|^2$ is small if the $\| \nabla \tau\|$ is small.

$f$ : network function

some notation:

$x(s)$ input image intensity
$s = (u, v)\in [0, 1]^2$ (continuous) pixel position

$\tau$ smooth deformation

$\tau x$ image deformed by $\tau$
such that $[\tau x](s)=x(s-\tau(s))$

$\tau(s) = (\tau_u(s),\tau_v(s))$ is a vector field

The deformation amplitude is measured by $$\| \nabla \tau\|^2=\int_{[0,1]^2}( (\nabla \tau_u)^2 + (\nabla \tau_v)^2 )dudv$$

\tau x

\tau

Negative empirical results

Previous empirical works show that small shifts of the input can significantly change the net output.

Issues:

consider images that have very different statistics than the actual data
not diffeomorphisms but cropping and resizing
it is not the absolute value of $\|f(x) - f(\tau x)\|^2$ that matters (see later).

Azulay and Weiss (2018); Dieleman et al. (2016); Zhang (2019) ...

Introduce a max-entropy distribution of diffeomorphisms of controlled magnitude

Our contribution:

Max-entropy model of diffeomorphisms

Goal: probe deep nets with typical diffeo of controlled norm $\| \nabla \tau\|$.
We write the field in real Fourier + boundary conditions: $$\tau_u=\sum_{i,j\in \mathbb{N}^+} C_{ij} \sin(i \pi u) \sin(j \pi v)$$
We want the distribution over $\tau$ that maximizes entropy with a norm constraint
and find that $\tau_u$ and $\tau_v$ are independent and have the same statistics and $C_{ij}$ are iid Gaussian random variables with $\langle C_{ij}^2 \rangle = \frac{T}{i^2 + j^2}$.

notation:

$x(s)$ input image intensity
$s = (u, v)\in [0, 1]^2$ (continuous) pixel position

$\tau$ smooth deformation

$\tau x$ image deformed by $\tau$
such that $[\tau x](s)=x(s-\tau(s))$

$\tau(s) = (\tau_u(s),\tau_v(s))$ is a vector field

\tau x

\tau

The deformation amplitude is measured by $$\| \nabla \tau\|^2=\int_{[0,1]^2}( (\nabla \tau_u)^2 + (\nabla \tau_v)^2 )dudv$$

some examples of diffeomorphisms on images

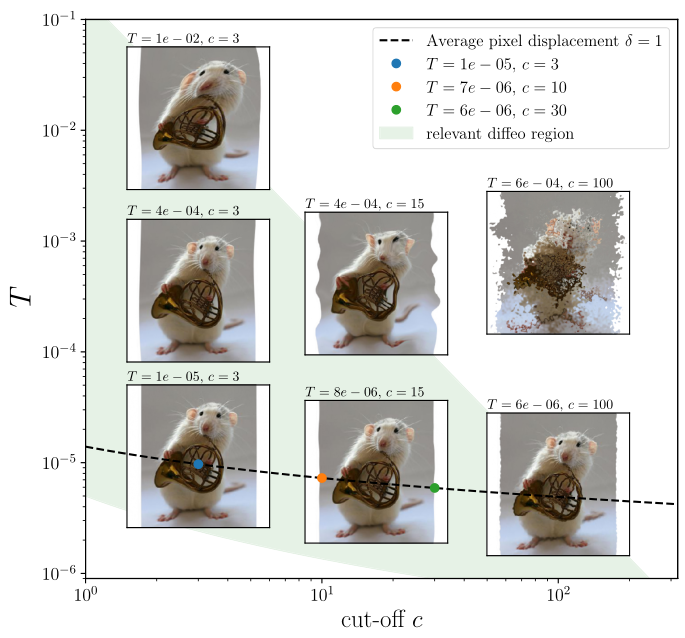
Introduce a max-entropy distribution of diffeomorphisms of controlled magnitude
Define the relative stability toward diffeomorphisms with respect to that of a random transformation, $R_f$

Our contribution:

Relative stability to diffeomorphisms

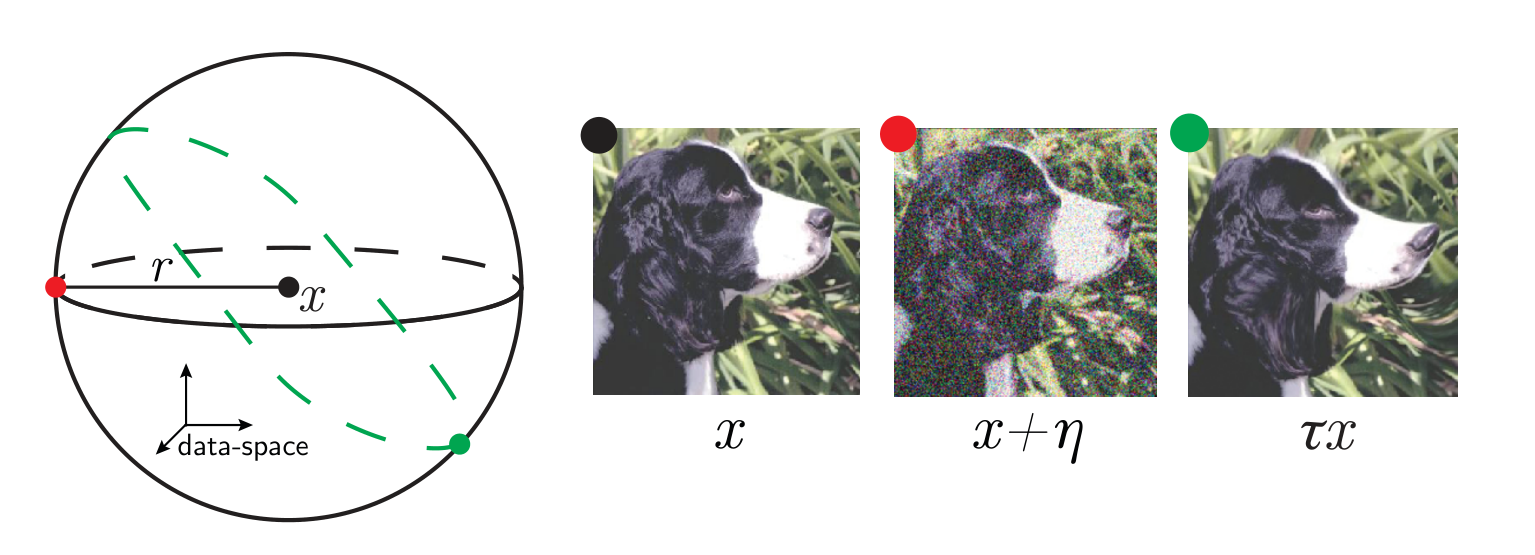
$x$ input image

$\tau$ smooth deformation

$\eta$ isotropic noise with $\|\eta\| = \langle\|\tau x - x\|\rangle$

$f$ network function

Goal: quantify how a deep net learns to become less sensitive
to diffeomorphisms than to generic data transformations

$$R_f = \frac{\langle \|f(\tau x) - f(x)\|^2\rangle_{x, \tau}}{\langle \|f(x + \eta) - f(x)\|^2\rangle_{x, \eta}}$$

Relative stability:

Introduce a max-entropy distribution of diffeomorphisms of controlled magnitude
Define the relative stability toward diffeomorphisms with respect to that of a random transformation, $R_f$
Study $R_f$ for different architectures and datasets both at initialization and after training.

Our contribution:

Probing neural nets with diffeo

$$R_f = \frac{\langle \|f(\tau x) - f(x)\|^2\rangle_{x, \tau}}{\langle \|f(x + \eta) - f(x)\|^2\rangle_{x, \eta}}$$

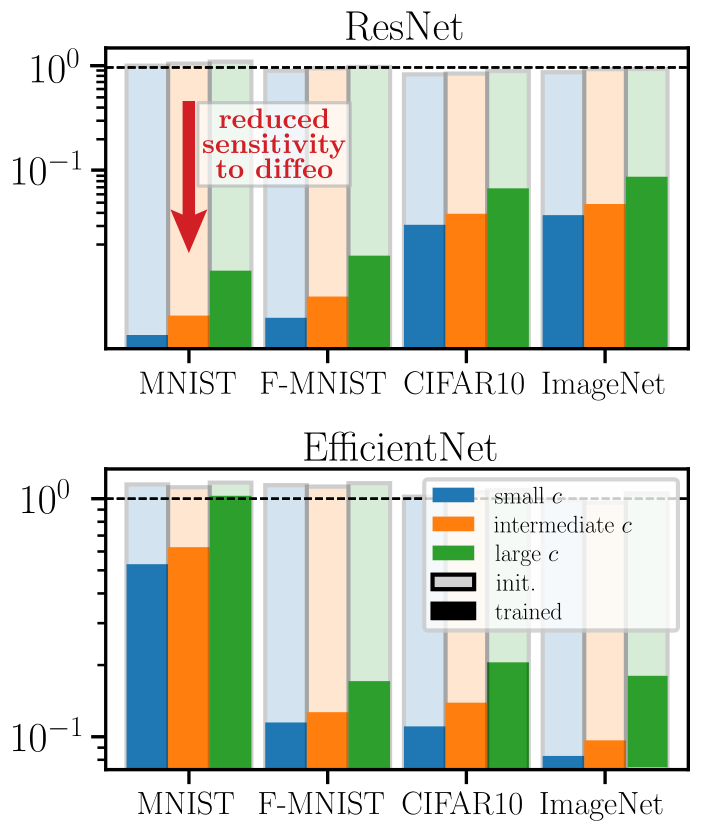
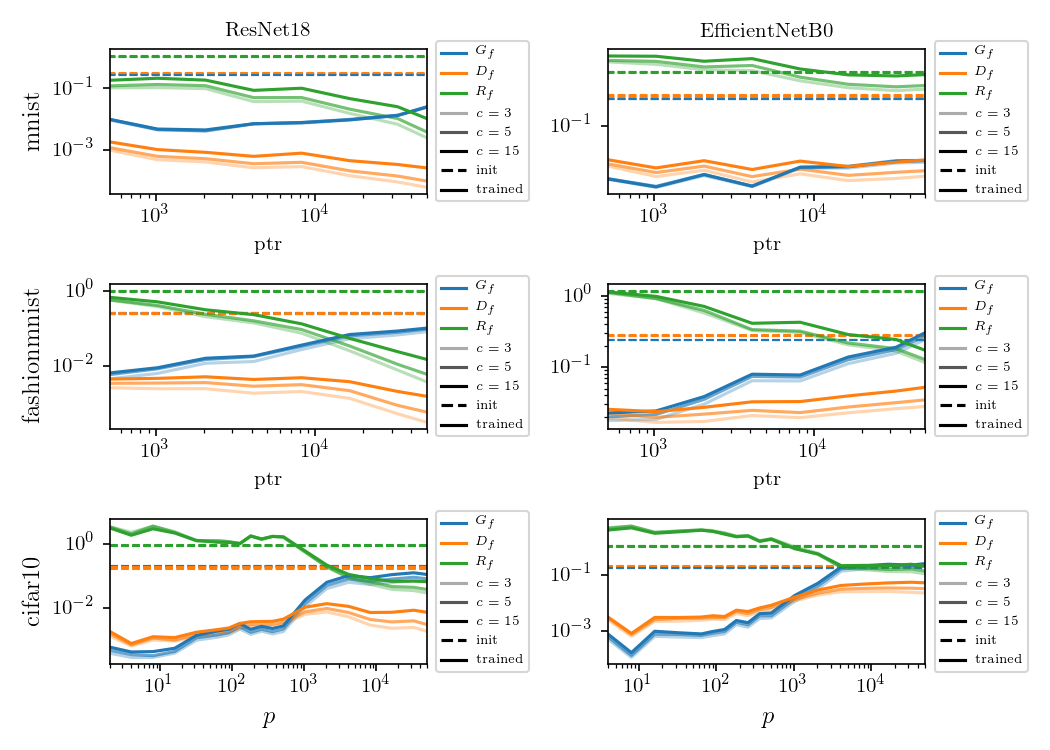
Results:

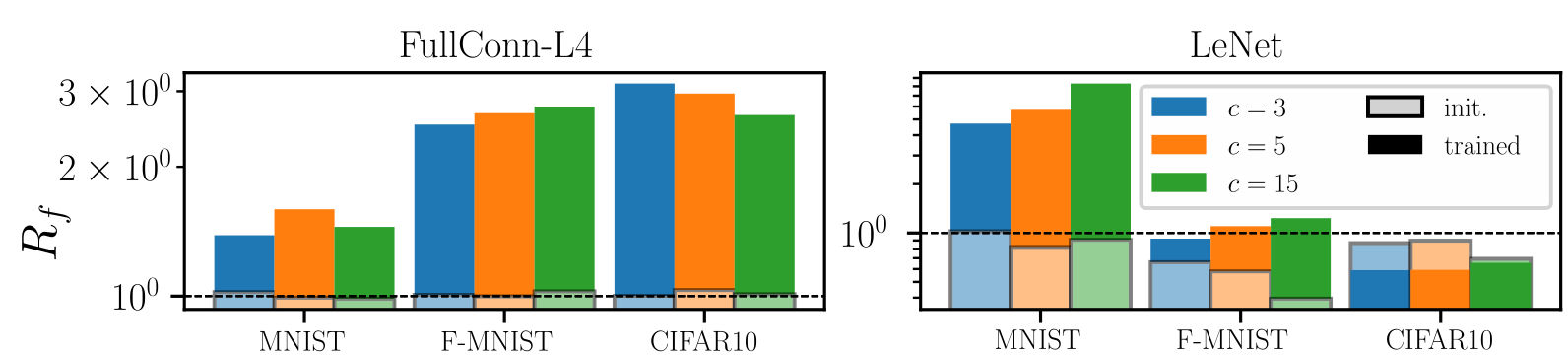
At initialization (shaded bars) $R_f \approx 1$ - SOTA nets don't show stability to diffeo at initialization.
After training (full bars) $R_f$ is reduced by one order of magnitude or two consistently across datasets and architectures.
By contrast, (2.) doesn't hold true for fully connected and simple CNNs.

Deep nets learn to become stable to diffeomosphisms!

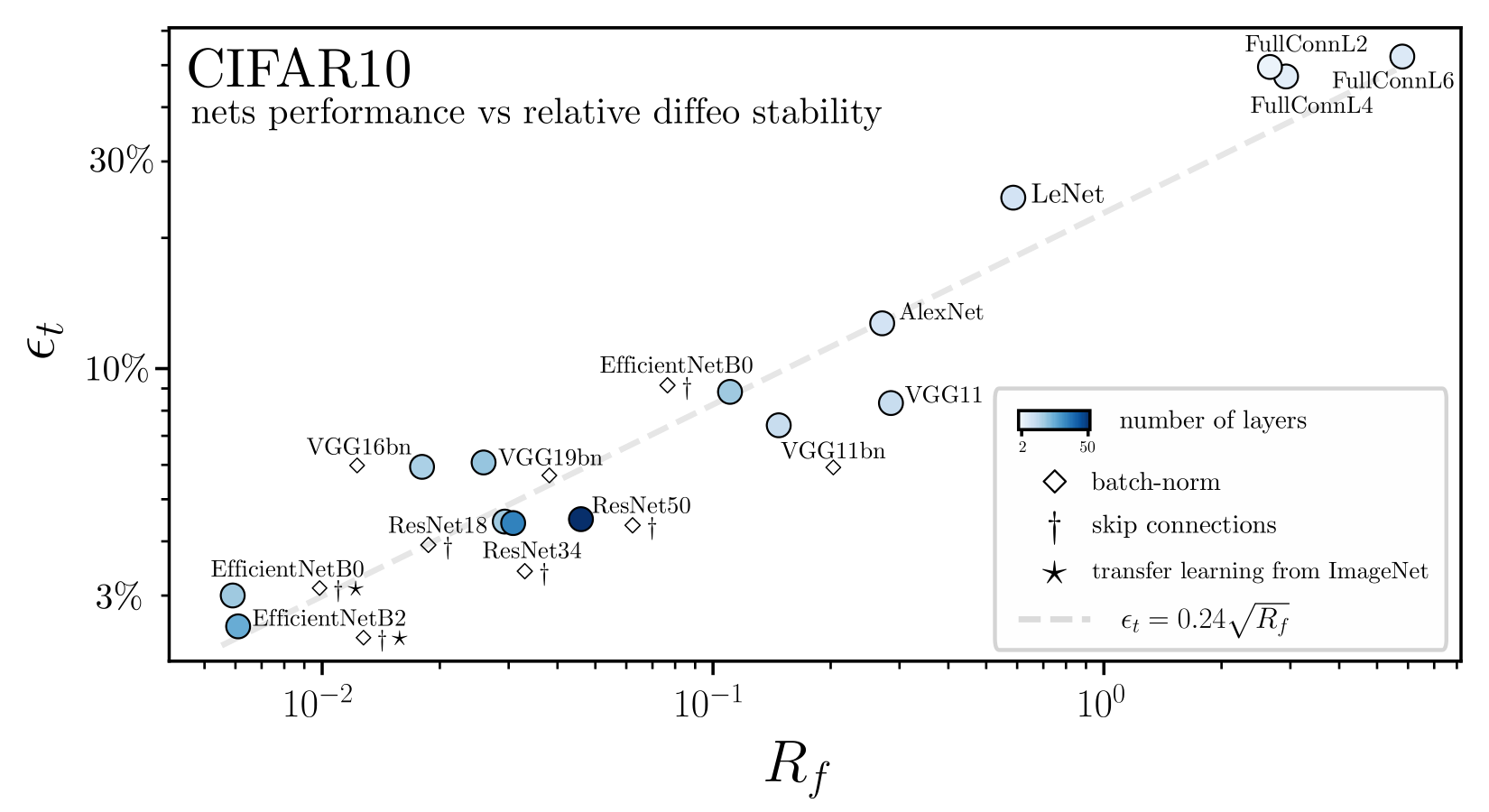
Relative stability to diffeomorphisms remarkably correlates to performance!

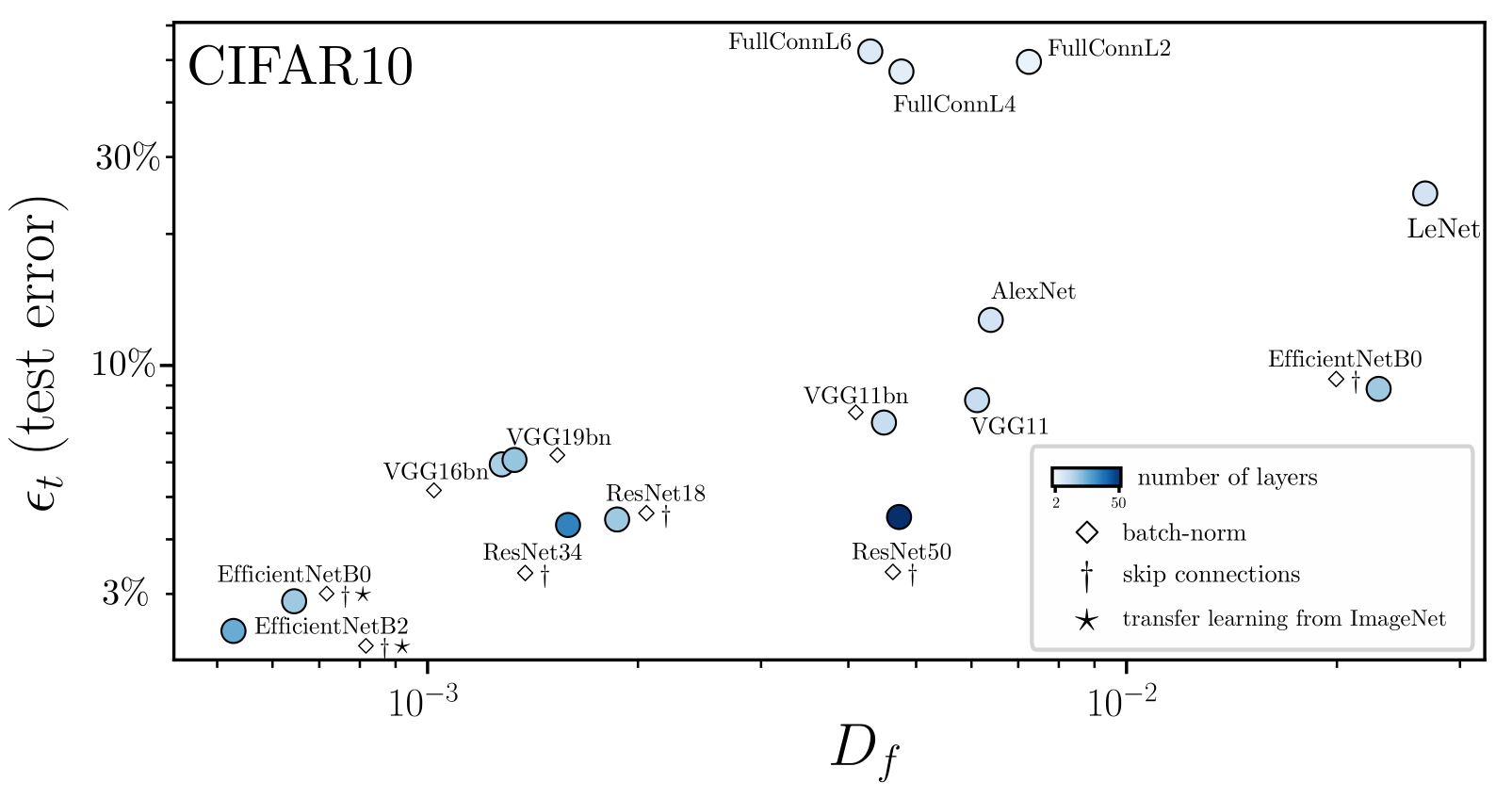
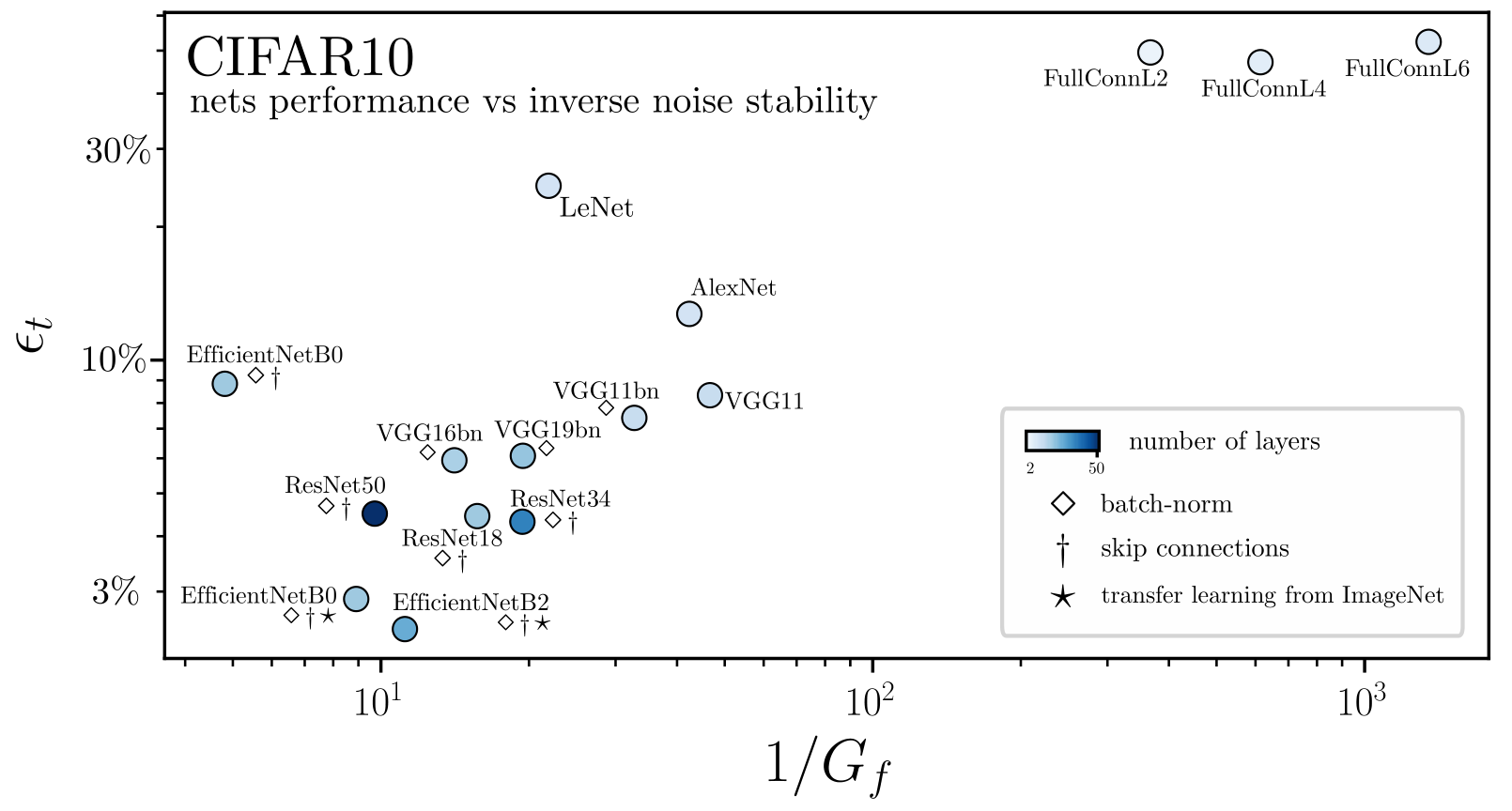
Why relative and not absolute stability?

Relative stability can be rewritten as

diffeo stability

G_f = \frac{\langle \|f(x + \eta) - f(x)\|^2\rangle_{x, \eta}}{\langle \|f(x) - f(z)\|^2\rangle_{x, z}}

D_f = \frac{\langle \|f(\tau x) - f(x)\|^2\rangle_{x, \tau}}{\langle \|f(x) - f(z)\|^2\rangle_{x, z}}

R_f=\frac{D_f}{G_f}

additive noise stability

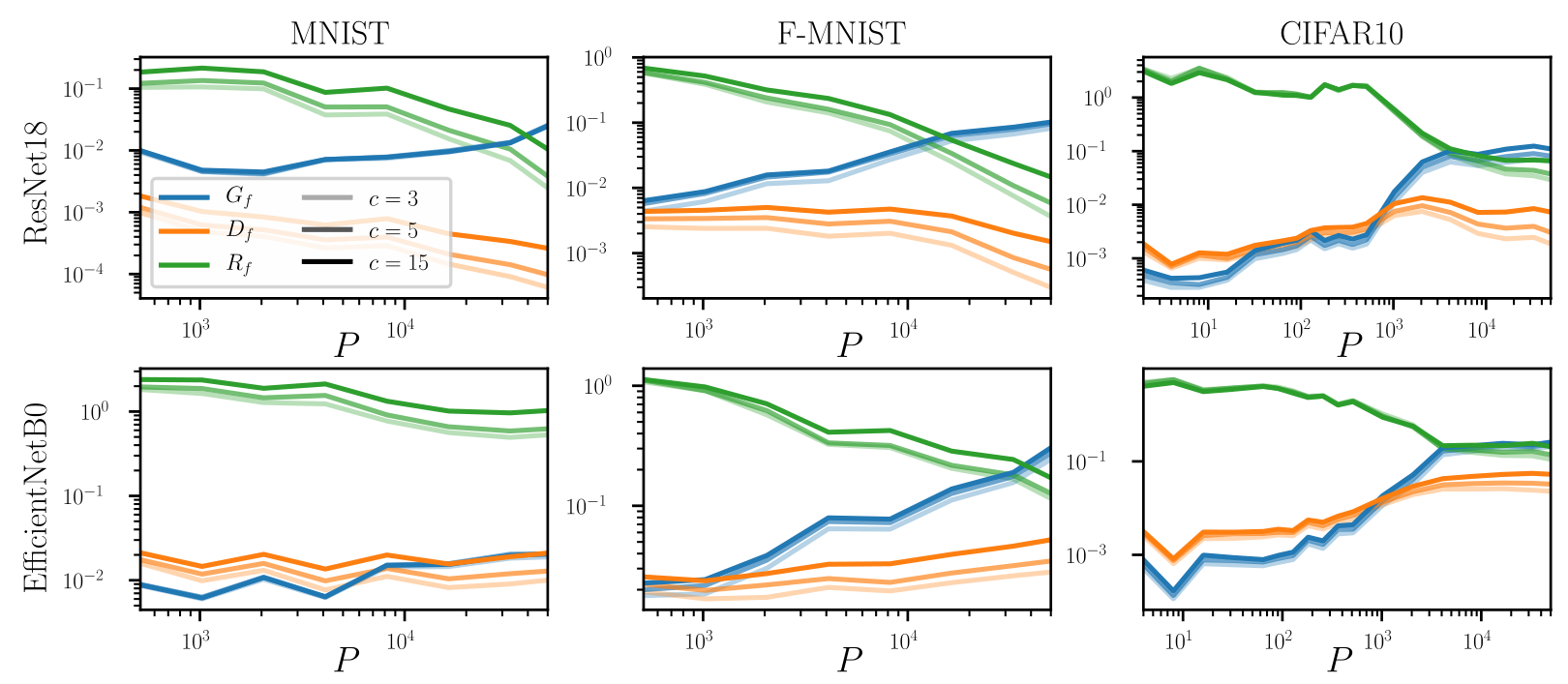
$P$ : train set size

$R_f$ monotonically decreases
$G_f$ monotonically increases:
the net function roughens as it needs to fit more and more points
$D_f$ does not behave universally because it contains two effects:
- roughening of the learned function
- invariance to diffeomorphisms.

Stability $D_f$ is not the good observable to characterize how deep nets learn diffeo invariance

As a function of the train set size $P$:

conclusions

We introduce a novel empirical framework to characterize diffeomorphisms stability in deep nets based on
- a max-entropy distribution of diffeomorphisms
- the realization that relative stability is the relevant observable
Main finding: relative stability correlates to performance
Max-entropy diffeomorphisms can be used for data augmentation
An estimation of $R_f$ can be used as a regularizer during training
Mechanistic understanding of how the network learn the invariance

future work

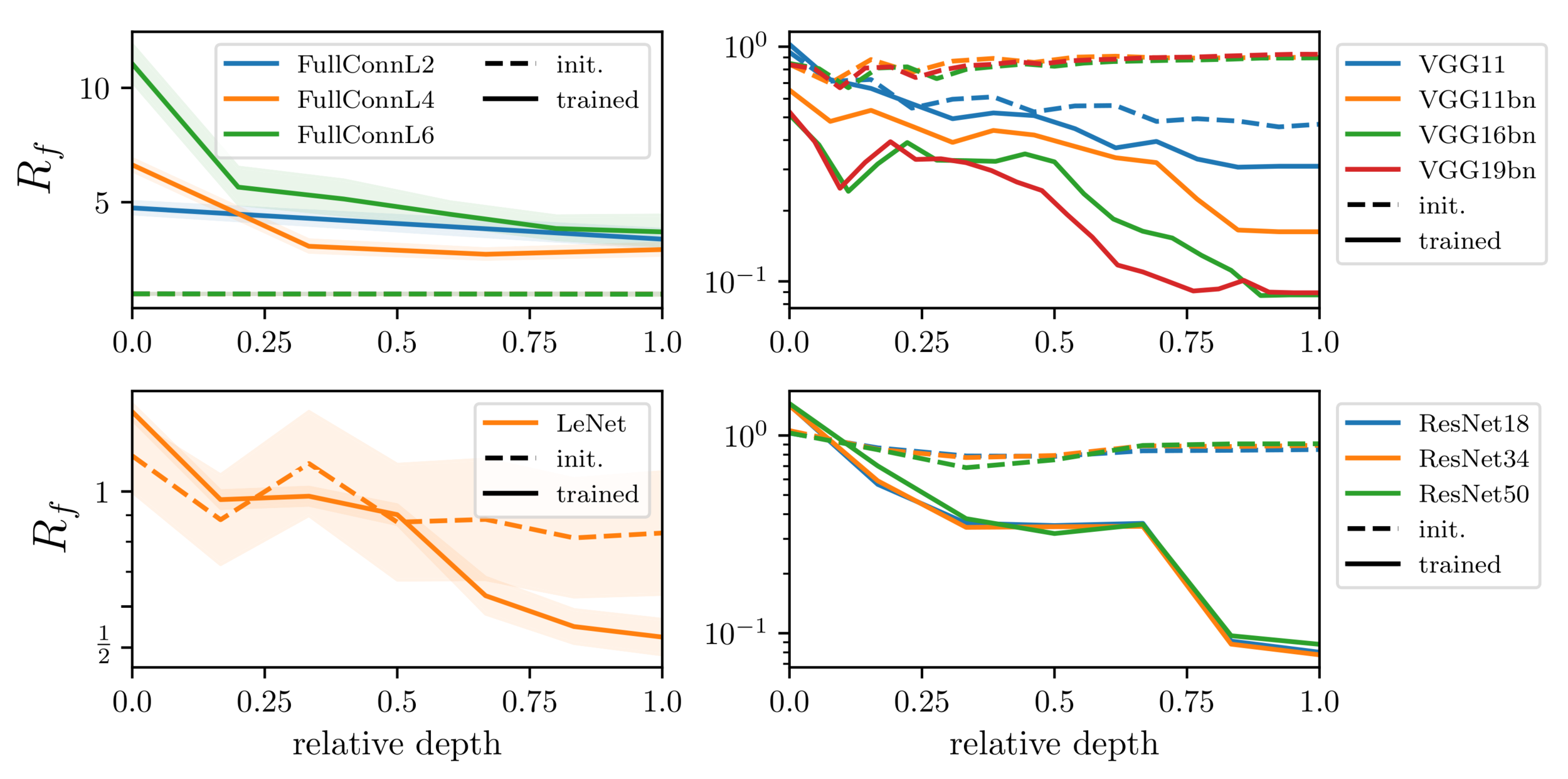
stability in depth:

slides.com/leopetrini

Thanks!