the role of adaptive pooling

PCSL retreat

Verbier, April 2022

Learning in convolutional neural networks:

The puzzling success of deep learning

Deep learning is incredibly successful in wide variety of tasks

Curse of dimensionality when learning in high-dimensions,
in a generic setting

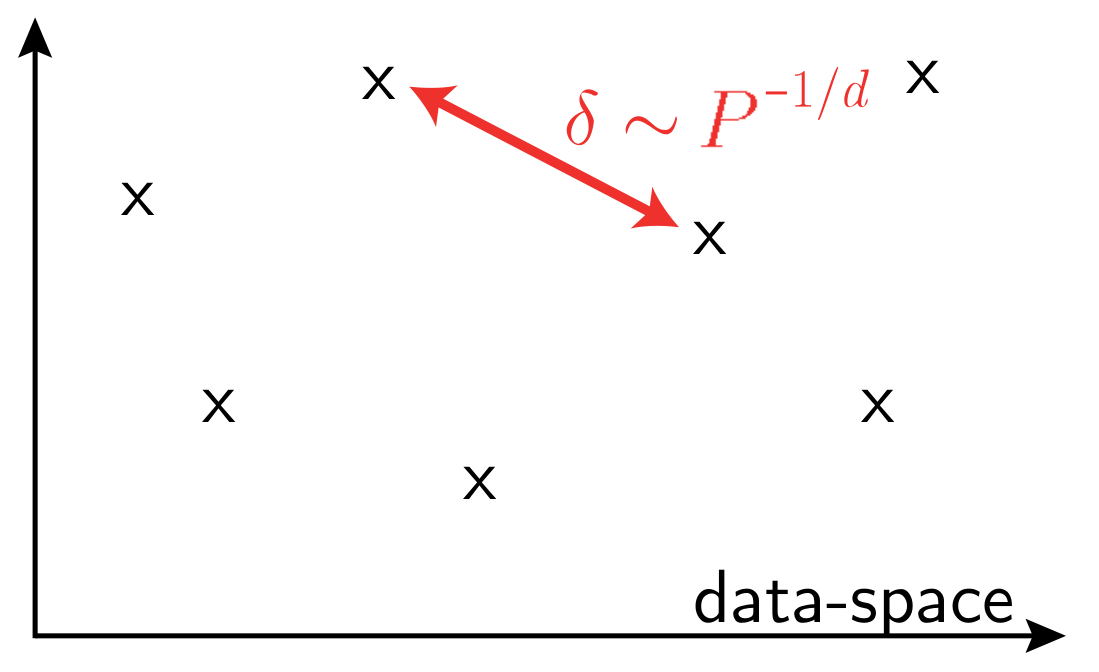
vs.

In high dimension, data that have little structure cannot be learned

$P$: training set size

$d$ data-space dimension

What is the structure of real data?

Cat

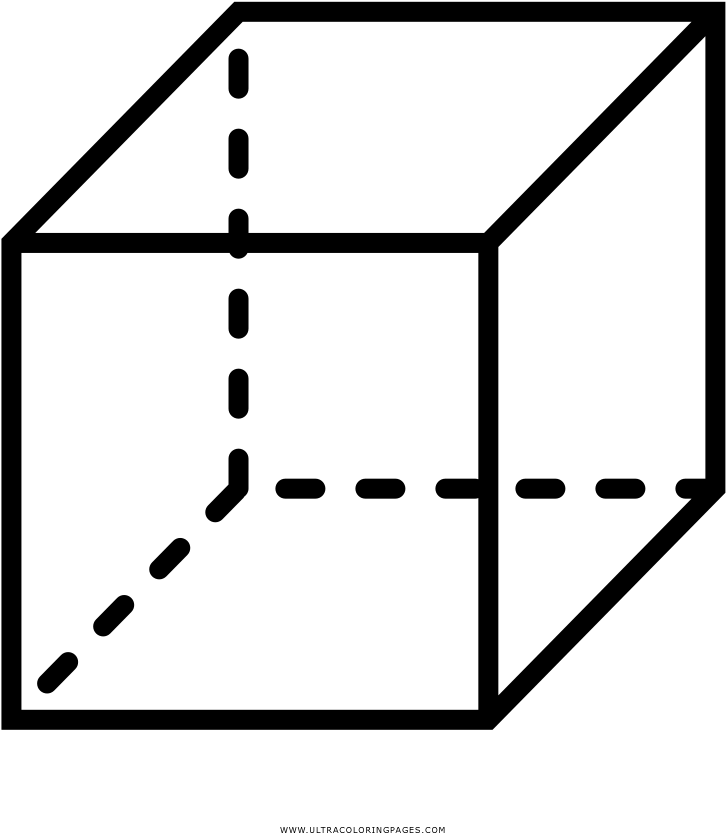
space of dimension $d$

cube of edge $L=1$

$L=1$

The volume of the cube is 1, we want to allocate that volume to $P$ smaller cubes, each containing a data-point.

Each smaller cube will have a volume of $1/P$ and side length:

$$l = \left( \frac{1}{P}\right)^{1/d}$$

$l$

the curse of dimensionality

Idea: there are directions in input space that the task is invariant to.
An example is the space of image translations - that is small though.
Space of smooth deformations is much larger - getting invariant to that can be key to escape the curse of dimensionality!

Invariances give structure to data-space

Bruna and Mallat (2013), Mallat (2016), ...

How to characterize such invariance?

$x-$translations

$y-$translations

(only two degrees of freedom)

\tau x

\tau

R_f = \frac{\langle\|f(\quad) - f(\quad)\|\rangle_{\;,}}{\langle\| f(\quad) - f(\quad)\|\rangle_{\;,}}

\tau x

\tau

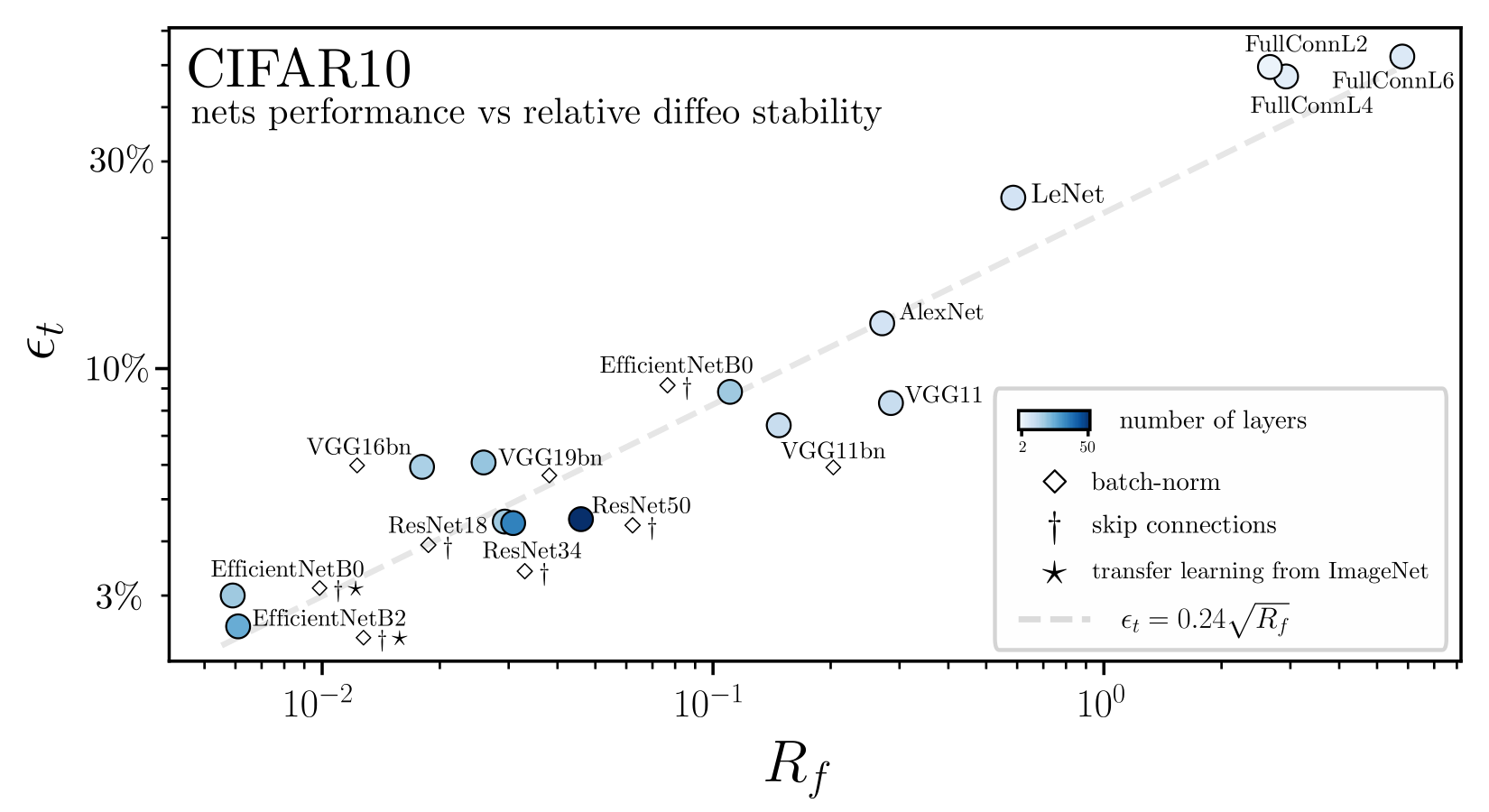
Such invariance can be characterized by the relative stability
Hypothesis: nets perform better and better by becoming more and more stable to diffeo

Measuring deformation invariance

= "cat"

Measuring deformation invariance

Measuring deformation invariance

Measuring deformation invariance

We define the relative stability to diffeomorphisms as

Hypothesis: nets perform better and better by becoming more and more stable to diffeo

R_f \approx \frac{\|\quad - \quad\|}{\|\quad - \quad\|}

Is this hyp. true?
Can we test it?

Relative stability to diffeomorphisms

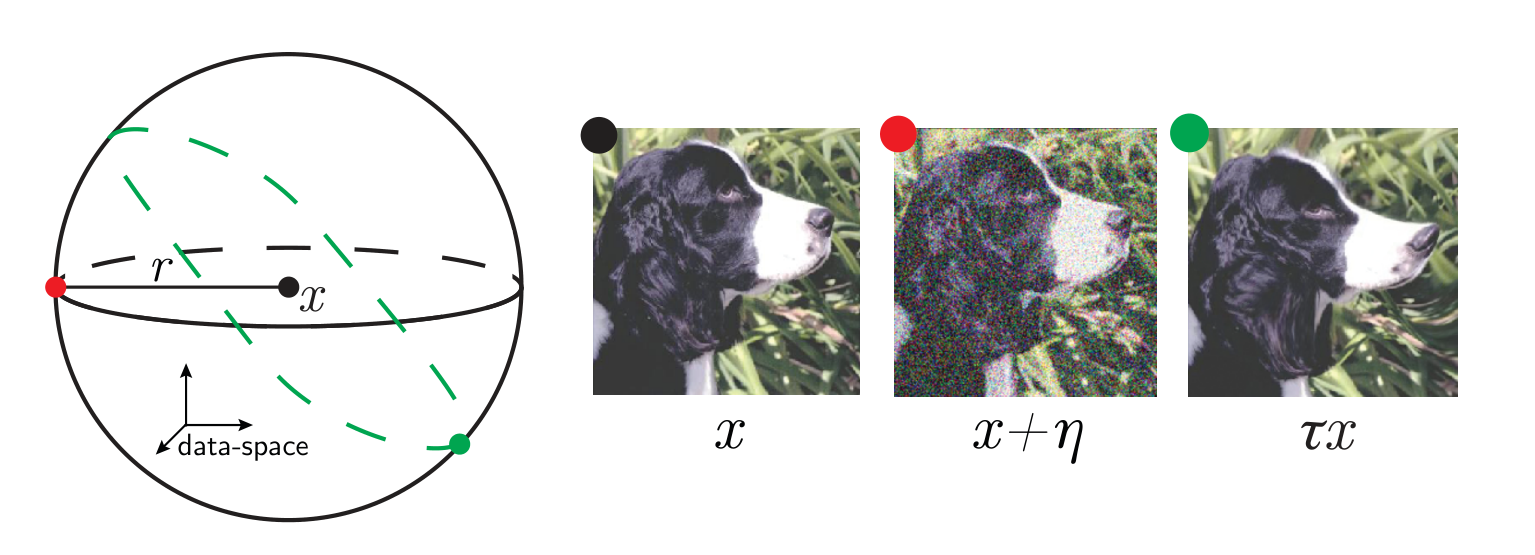
$x$ input image

$\tau$ smooth deformation

$\eta$ isotropic noise with $\|\eta\| = \langle\|\tau x - x\|\rangle$

$f$ network function

Goal: quantify how a deep net learns to become less sensitive
to diffeomorphisms than to generic data transformations

$$R_f = \frac{\langle \|f(\tau x) - f(x)\|^2\rangle_{x, \tau}}{\langle \|f(x + \eta) - f(x)\|^2\rangle_{x, \eta}}$$

Relative stability:

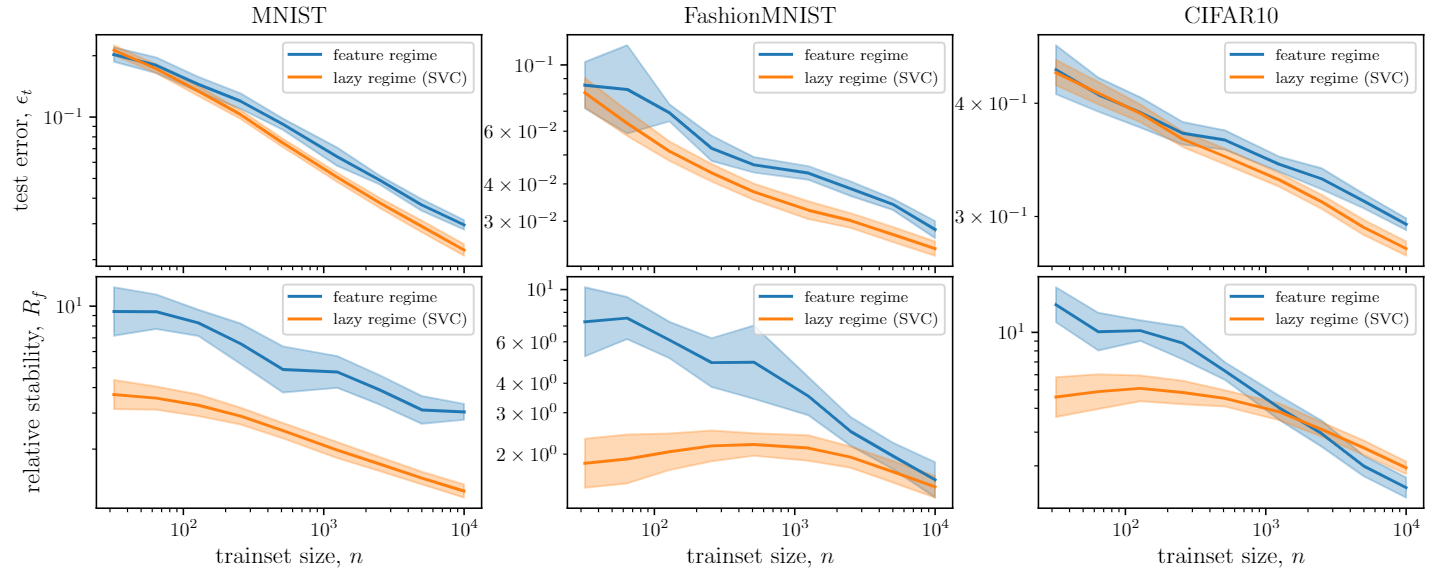
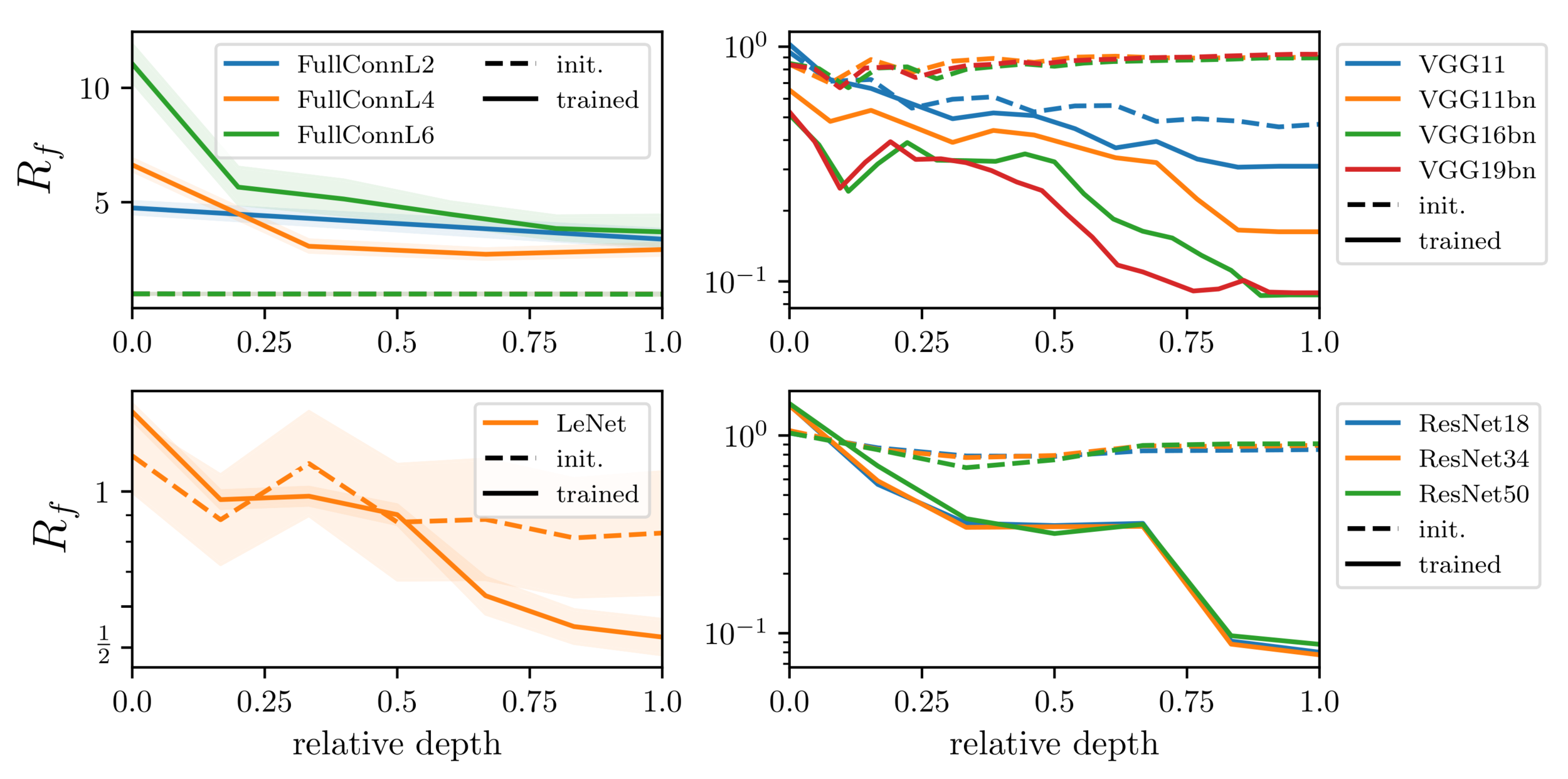
Relative stability to diffeomorphisms remarkably correlates to performance!

2. How do CNNs build diffeo stability and perform well?

1. How to rationalize this behavior?

R_f = 1

Why FC nets unlearn diffeo stability?
How do CNNs build diffeo stability?

Outline

A spherically symmetric dataset

\mathbb{S}^{1}

x_1

x_2

\mathbf x_\mu

Dataset: $\{$$\mathbf x_\mu$$, y_\mu\}$ with $\mathbf x_\mu$$ \in \mathbb{S}^{d-1}$ and $y_\mu = 1$

A spherically symmetric dataset

\mathbb{S}^{1}

\mathbf x_\mu

x_1

x_2

weights $\mathbf w_h$ before training

Dataset: $\{$$\mathbf x_\mu$$, y_\mu\}$ with $\mathbf x_\mu$$ \in \mathbb{S}^{d-1}$ and $y_\mu = 1$
Architecture: Fully connected network: $f(\mathbf x) = \frac{1}{H}\sum_{h=1}^H c_h\, \sigma($$\mathbf w_h$$\cdot \mathbf x)$
Algorithm: gradient descent on the mean square loss: $\mathcal{L} = \frac{1}{2P} \sum_{\mu = 1}^P $$(f(\mathbf x_\mu) - y_\mu)^2$

A spherically symmetric dataset

Dataset: $\{$$\mathbf x_\mu$$, y_\mu\}$ with $\mathbf x_\mu$$ \in \mathbb{S}^{d-1}$ and $y_\mu = 1$
Architecture: Fully connected network: $f(\mathbf x) = \frac{1}{H}\sum_{h=1}^H c_h\, \sigma($$\mathbf w_h$$\cdot \mathbf x)$
Algorithm: gradient descent on the mean square loss: $\mathcal{L} = \frac{1}{2P} \sum_{\mu = 1}^P $$(f(\mathbf x_\mu) - y_\mu)^2$

\mathbb{S}^{1}

x_1

x_2

\mathbf x_\mu

after training the

symmetry is preserved

\mathbb{S}^{1}

\mathbf x_\mu

x_1

x_2

after training the

symmetry is BROKEN

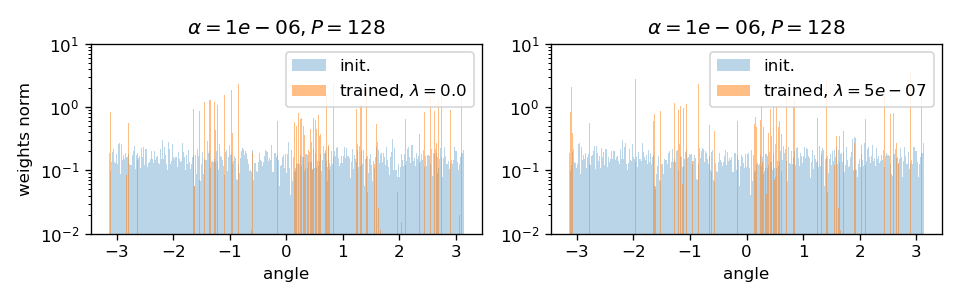
lazy regime

feature regime

evidence: sparsification

LAZY REGIME

FEATURE REGIME

A spherically symmetric dataset to gain insights on real images

Dataset: $\{$$\mathbf x_\mu$$, y_\mu\}$ with $\mathbf x_\mu$$ \in \mathbb{S}^{d-1}$ and $y_\mu = 1$
Architecture: Fully connected network: $f(\mathbf x) = \frac{1}{H}\sum_{h=1}^H c_h\, \sigma($$\mathbf w_h$$\cdot \mathbf x)$
Algorithm: gradient descent on the mean square loss: $\mathcal{L} = \frac{1}{2P} \sum_{\mu = 1}^P $$(f(\mathbf x_\mu) - y_\mu)^2$

\mathbb{S}^{d-1}

x_1

x_2

\mathbf x_\mu

weights $\mathbf w_h$ after training

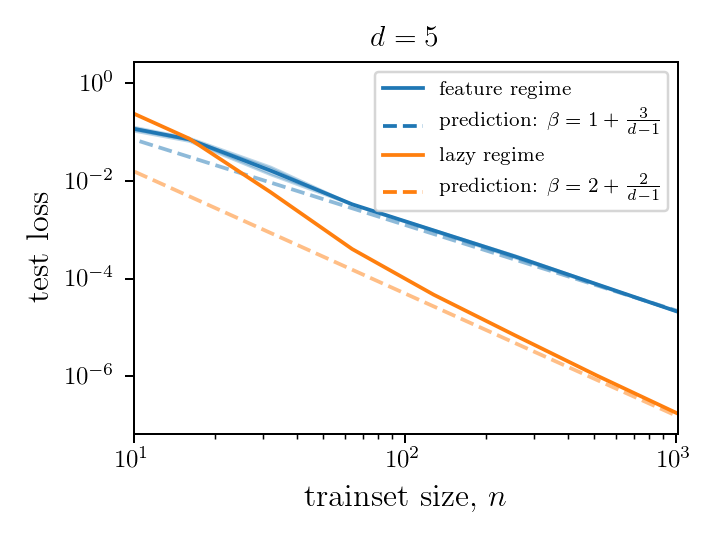
Lazy vs. feature performance in the spherical model

As a result, lazy performs better and is more stable to rotations.

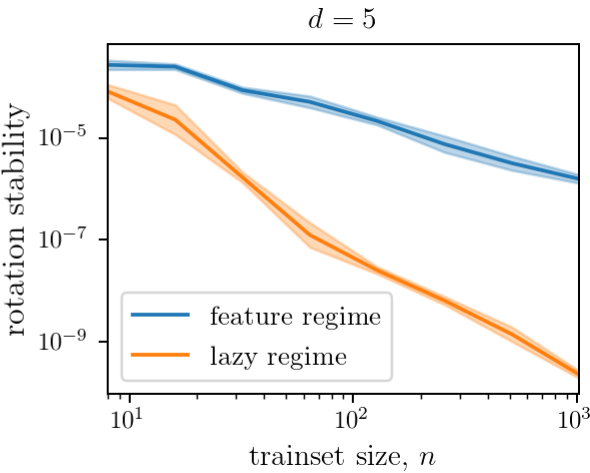
Rotation stability: $$S = \langle \|f(x) - f(R_\theta x)\|^2\rangle_{x, \theta}$$

To recap:

If we are given a dataset with a spherical symmetry and our model is correctly initialized:

The lazy regime will preserve the symmetry
The feature regime will overfit the training data and break the symmetry.

The spherical model rationalizes real-data findings

Spherical model

Images

Spherical symmetry
Training a FC network in the feature regime breaks the symmetry

Local deformations "symmetry"
Training a FC network in the feature regime worsen the invariance to diffeo

This is because all directions in input space should be treated equally but feature "overfits" some of them
By contrast, the lazy regime has a good prior at initialization and performs better

Neighboring pixels should be treated equally for local deformation invariance to hold

Feature breaks local deformation symmetry $\rightarrow$ it "overfits" some specific pixels
For the analogy to hold, lazy regime should have a better prior as it treats all pixels equally, indeed:

4 neigh. pixels

arrows: deformation

Why FC nets unlearn diffeo stability?
How do CNNs build diffeo stability?

The poor choice of architecture is such that the feature regime breaks the symmetry by overfitting pixels.

Outline

CNNs building block: the convolutional layer

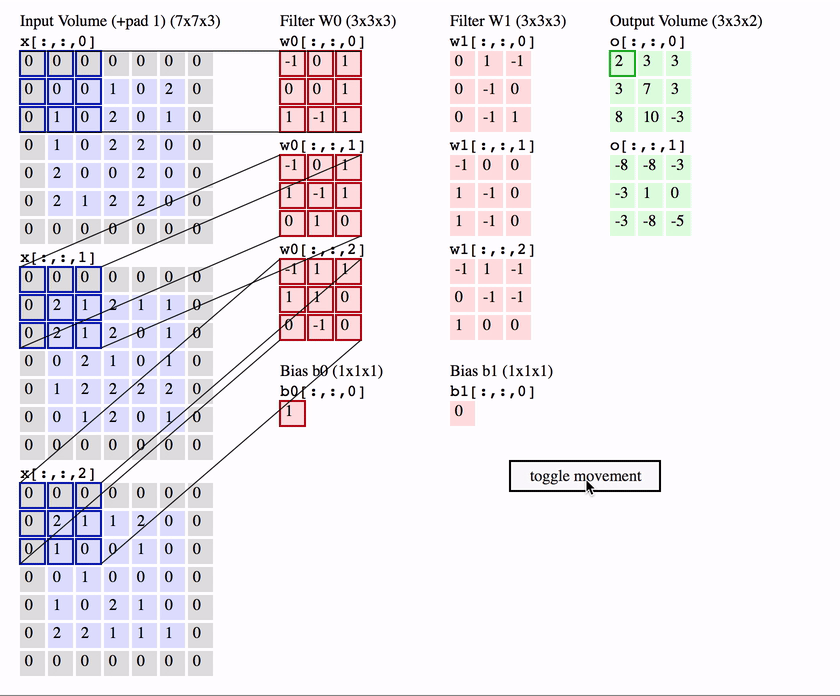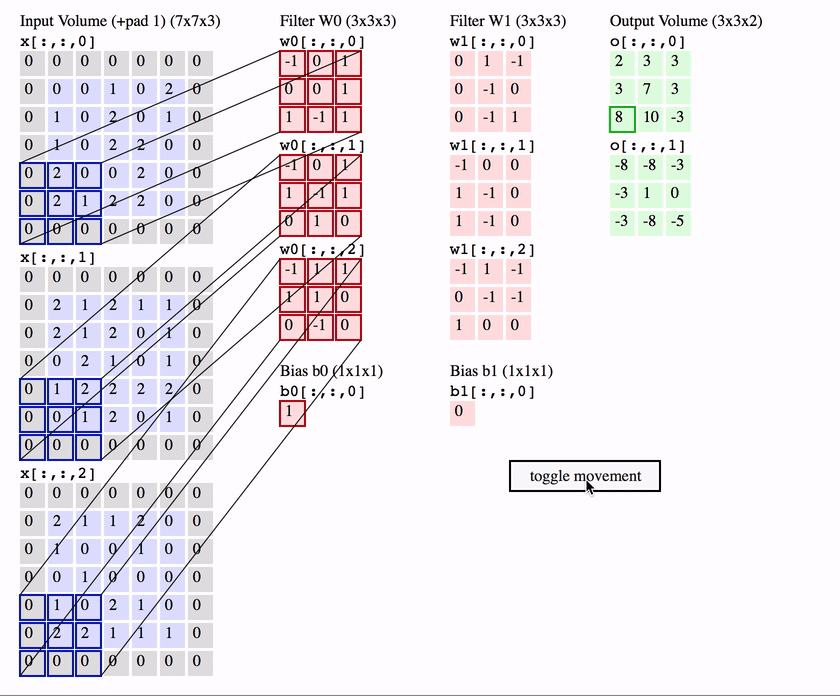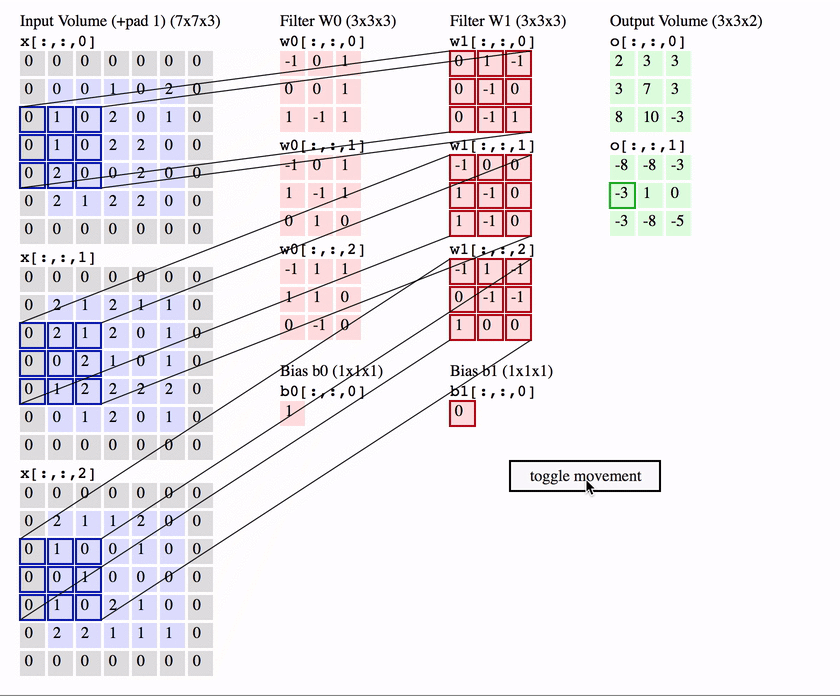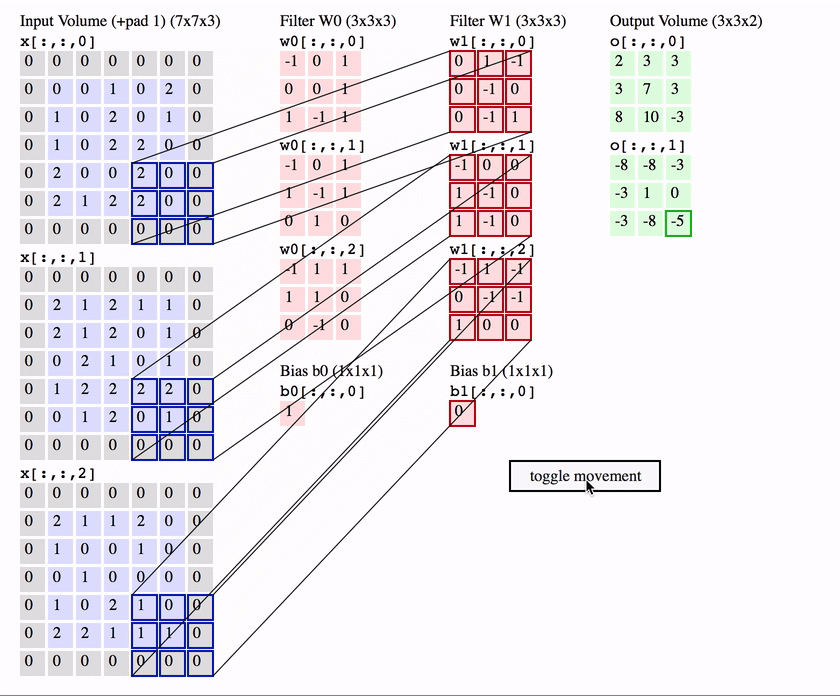
channel 1

channel 2

output (activation map)

input image

a non-linearity is applied here element-wise,
e.g. $\text{ReLU}(x) = \max(0, x)$

A convolutional neural network:

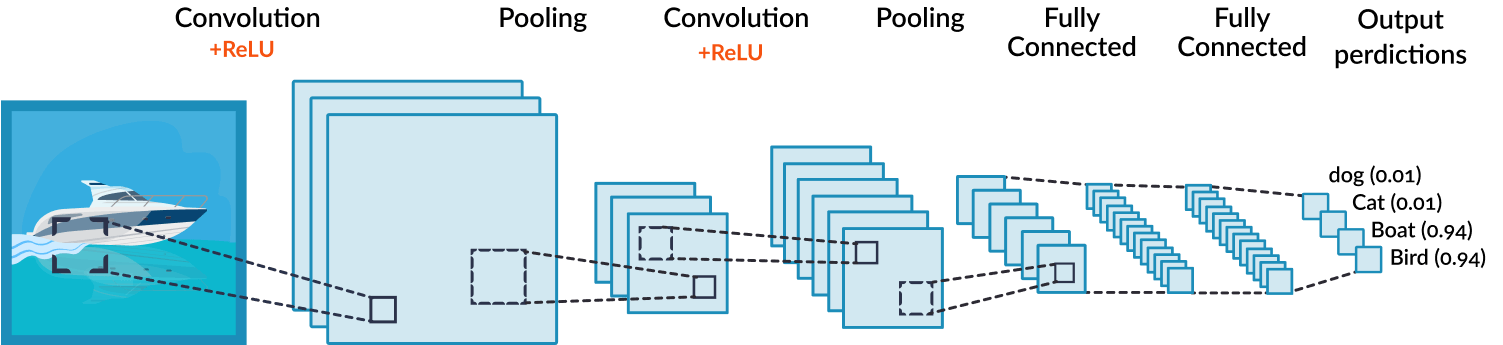
Stacking together many convolutional layers

Which parts of the network give relative stability?

Relative stability to diffeo is achieved layer-by-layer:

R_f

\text{relative depth}

Which mechanism(s) can give stability in a layer?

Which operations give relative stability to diffeo?

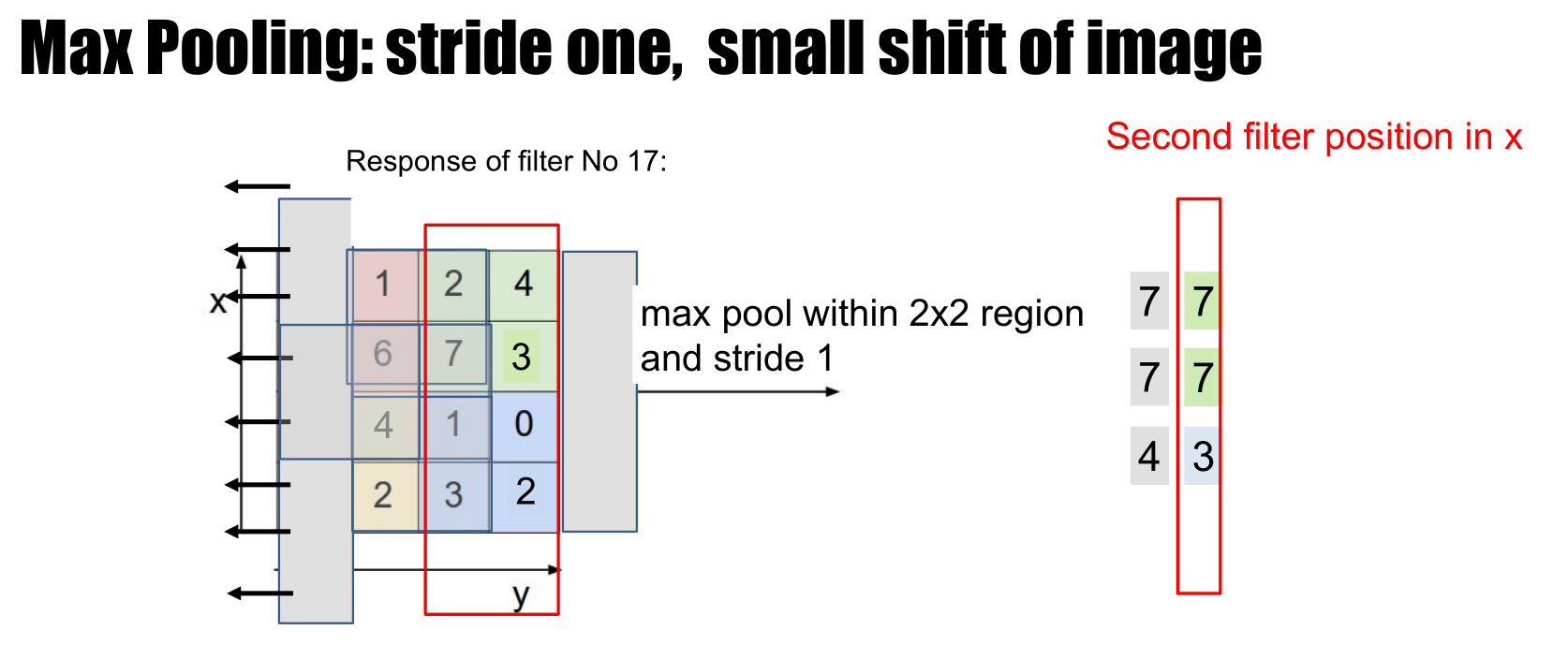
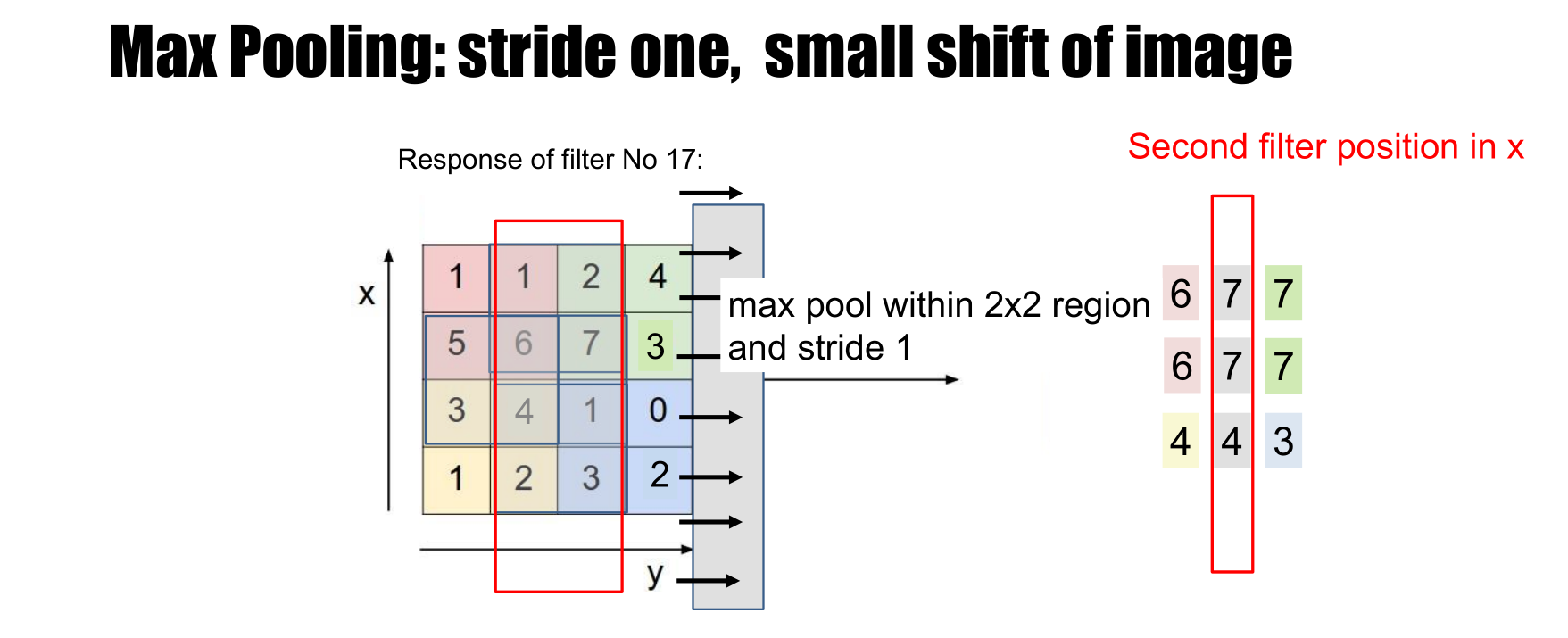
Spatial pooling

Channel pooling

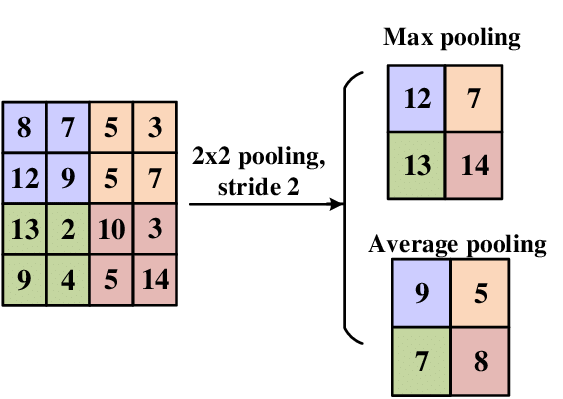
Average pooling can be learned by making filters low pass

Channel pooling can be learned by properly coupling filters together

Reduce the resolution of the feature maps by aggregating pixel values
Gives stability to local translations

Filters of different channels reproduce a symmetry in the data and get coupled together.
Can give stability to any local transformation.

\text{sum} = 1.2

$w\cdot x=$

$1.0$

0.2

filters $w$

input $x$

0.2

$1.0$

rotated input

\text{sum} = 1.2

filters $w$

input $x$

$w\cdot x=$

$1.0$

0.2

\sum (\dots) = 1.2

$1.0$

0.2

\sum (\dots) = 1.2

rotated input

filters $w$

input $x$

$w\cdot x=$

$1.0$

0.2

0.1

\sum (\dots) = 1.3

$1.0$

0.2

0.1

\sum (\dots) = 1.3

rotated input

Disentangling spatial and channel pooling in DNNs

Which one gives the observed relative stability in DNNs?

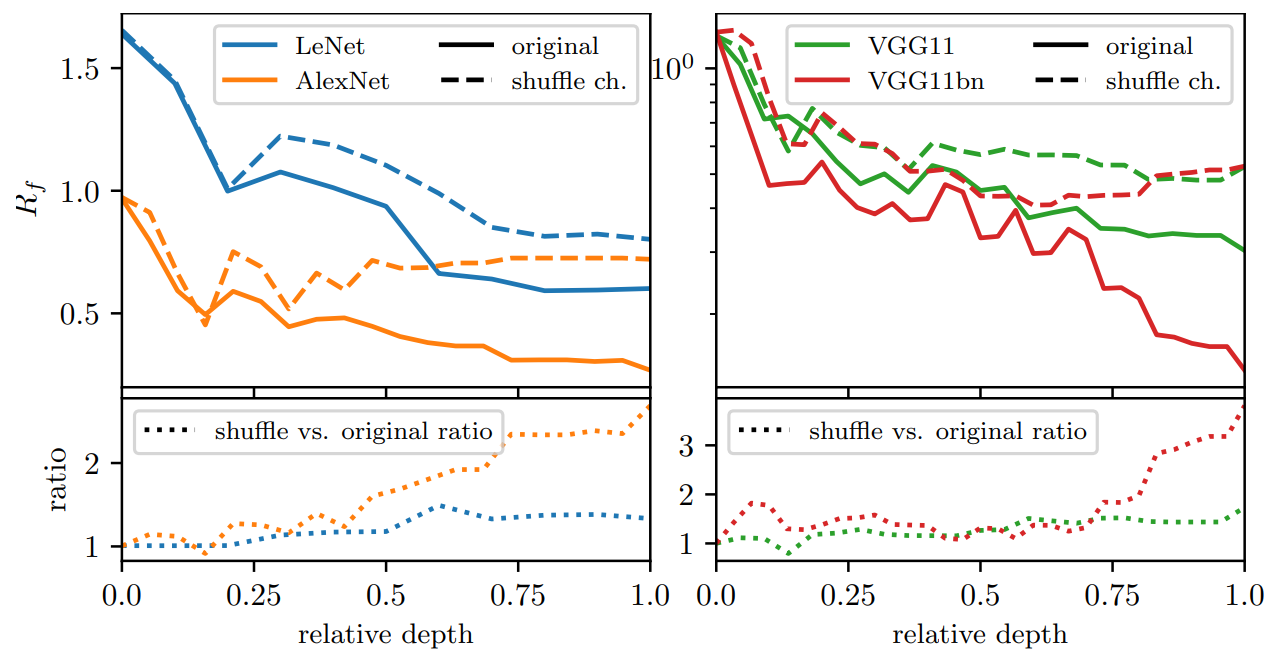
Filter pooling: 1st half of the network
Channel pooling: 2nd half of the network

Filter pooling is related to the filters frequencies
Channel pooling to how filters in different channels are coupled together
Idea: if we shuffle the connections between channels we destroy channel pooling while leaving filter pooling intact:

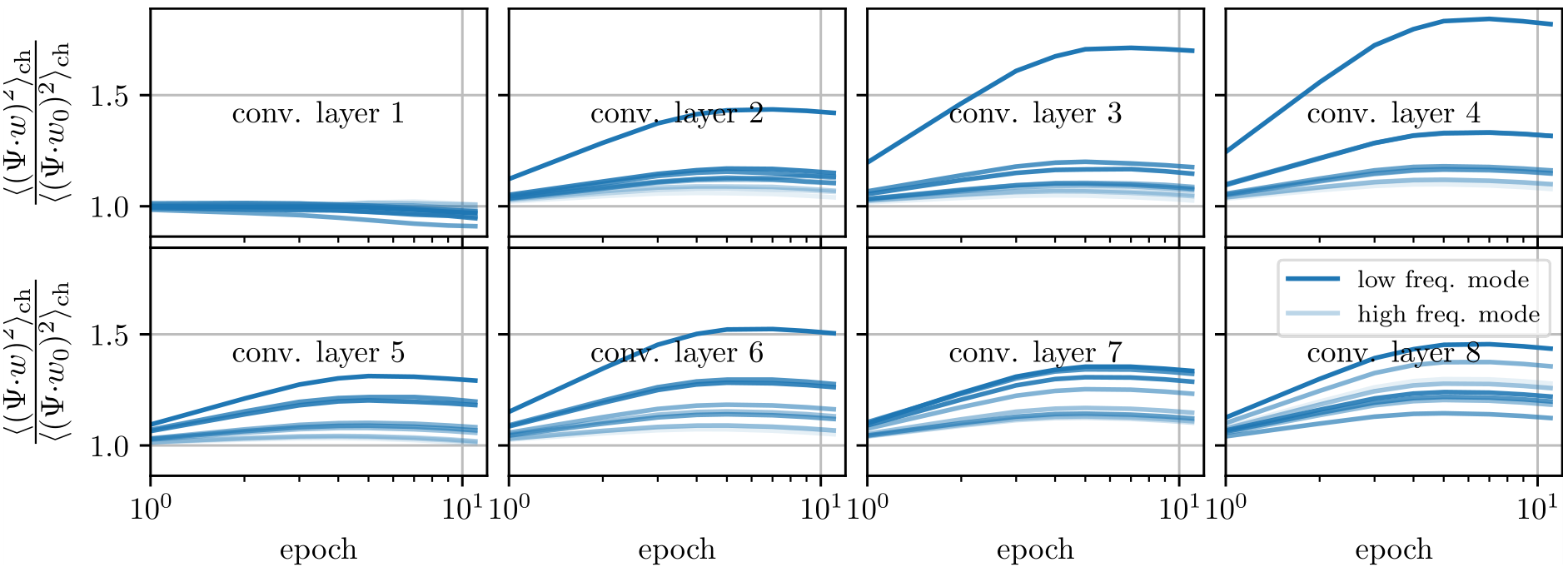
We take a basis that is the eigenvectors of the Laplacian on the 3x3 grid and follow weigths evolution on each of the components and average over the channels:

$$c_{t, \lambda} = \langle (w_{\rm{ch}, t} \cdot \Psi_\lambda )^2\rangle_{\rm{ch}}$$

we plot $$\frac{c_{t, \lambda}}{c_{t=0, \lambda}}$$

Weights become low-pass with training

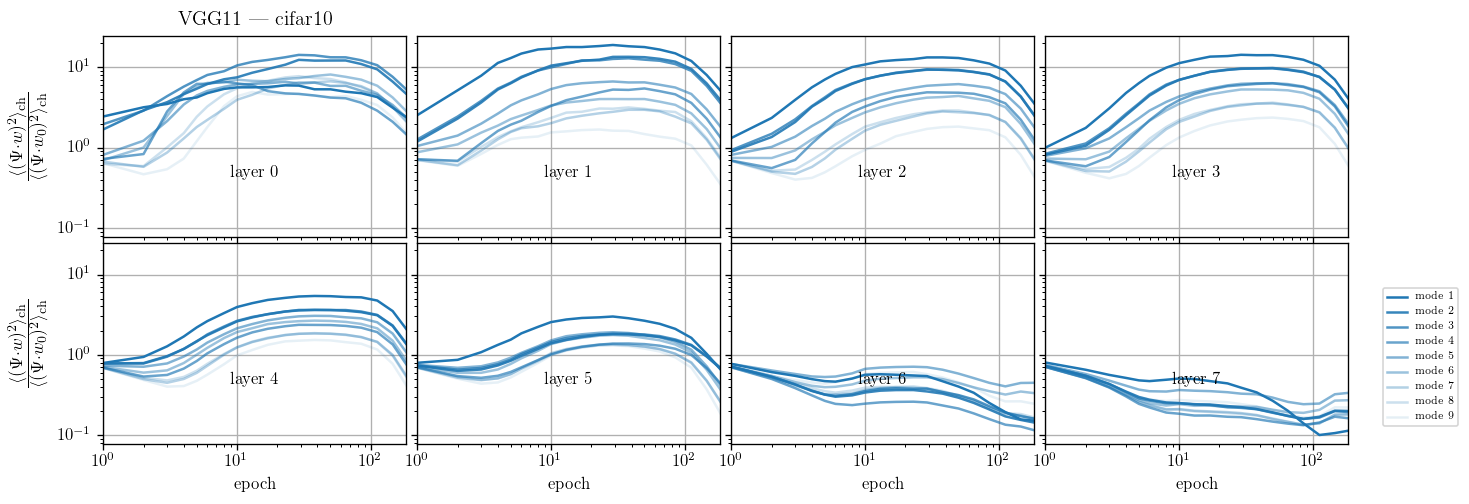
Additional evidence for filter pooling:

Filters actually learn to pool!

A data model for filter pooling

A model for filter pooling

Goal: build a data model in which learning to do filter pooling is needed to learn the task

image frame (e.g. 32x32 pixels)

Background value = 0
Two pixels of value +1

data-points $x_\mu\in \mathbb{R}^{d\times d}$

labels $y_\mu$

Euclidean distance, $\delta_\mu$

$$y_\mu = \text{sign} (\xi - \delta_\mu)$$

A network needs to learn to pool at the good length-scale $\xi$ to generalize

data-set $\{x_\mu, y_\mu\}$

Adaptive pooling model can reproduce real-data obervations

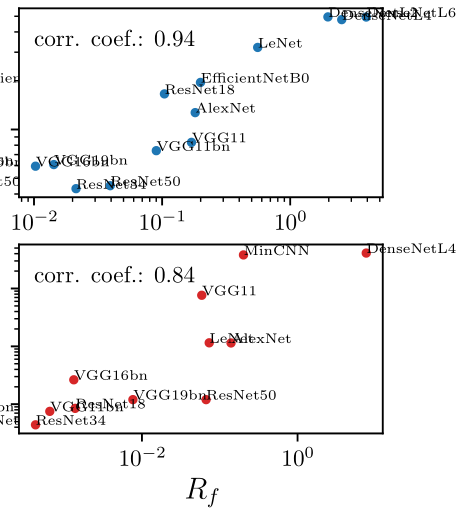
Test error is strongly correlated to relative stability
Filters become low-frequency with training

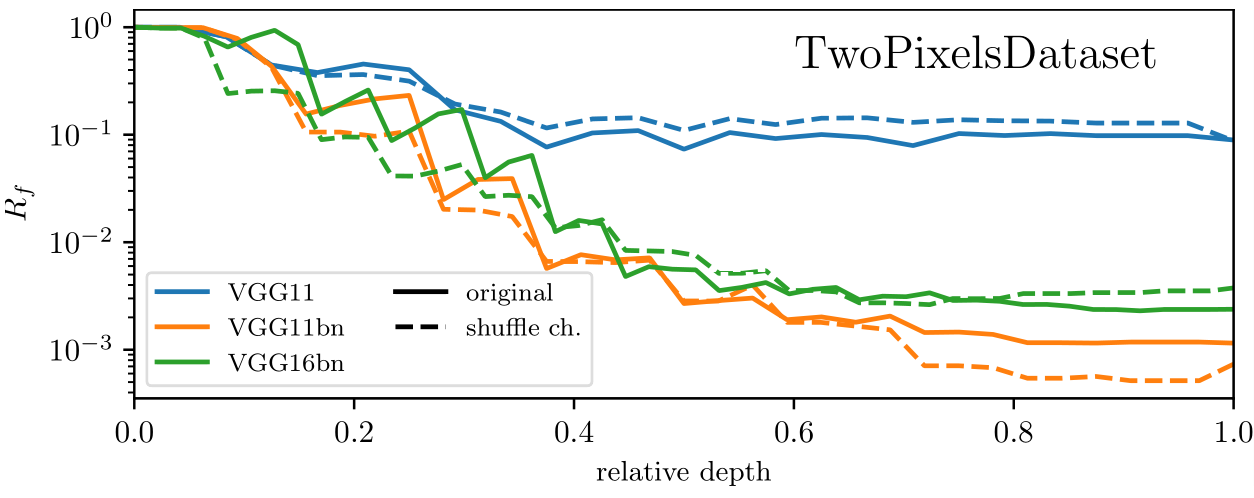
As expected, channel pooling is not present (i.e. shuffling channels has no effect in terms of relative stability).

Can we build a theory for the adaptive pooling model to rationalize real-data findings?

Why FC nets unlearn diffeo stability?
How do CNNs build diffeo stability?

The poor choice of architecture is such that the feature regime breaks the symmetry by overfitting pixels.

We find evidence of both filter and channel pooling playing a role
We have a model for adaptive filter pooling that can reproduce real-data phenomenology

Outline

A simple convolutional network 1/2

Input

Channel 1

Channel H

Channel 1

Channel H

L hidden layers

\text{ReLu}(p_1*w_1 +b_1)

p_1

w_1

A simple convolutional network 2/2

Channel 1

Channel H

Global Average Pooling of each channel:

to enforce translational invariance within it

Output $f_p$

Our strategy

We consider the TwoPixelsDataset in one dimension, with Periodic Boundary Conditions and length $l=32$.

d=5

We want to look at how the CNN builds up adaptive pooling, i.e. how it recognizes the scale $\xi$.
We try to propose a solution (i.e. a choice of parameters as filters and bias) which can capture the solution reached by the CNN.

Solution 1: low-frequency filters 1/2

Layer 1

Input

All filters like that, zero bias

We choose $\xi =7$ and filter size $s = 3$

At layer $k$, the receptive field of a single neuron is $(2k+1)$: given $\xi=7$, the layer $\tilde{k}$ where the scale can be seen is at $\tilde{k}=3$

For layers $k<\tilde{k}$: as above.

Solution 1: low-frequency filters 2/2

Layer $\tilde{k}$

-1 bias

Sign of positive interference!

Output: $f_p(x)=f_p(d)=\text{ReLu}(\xi-d)$

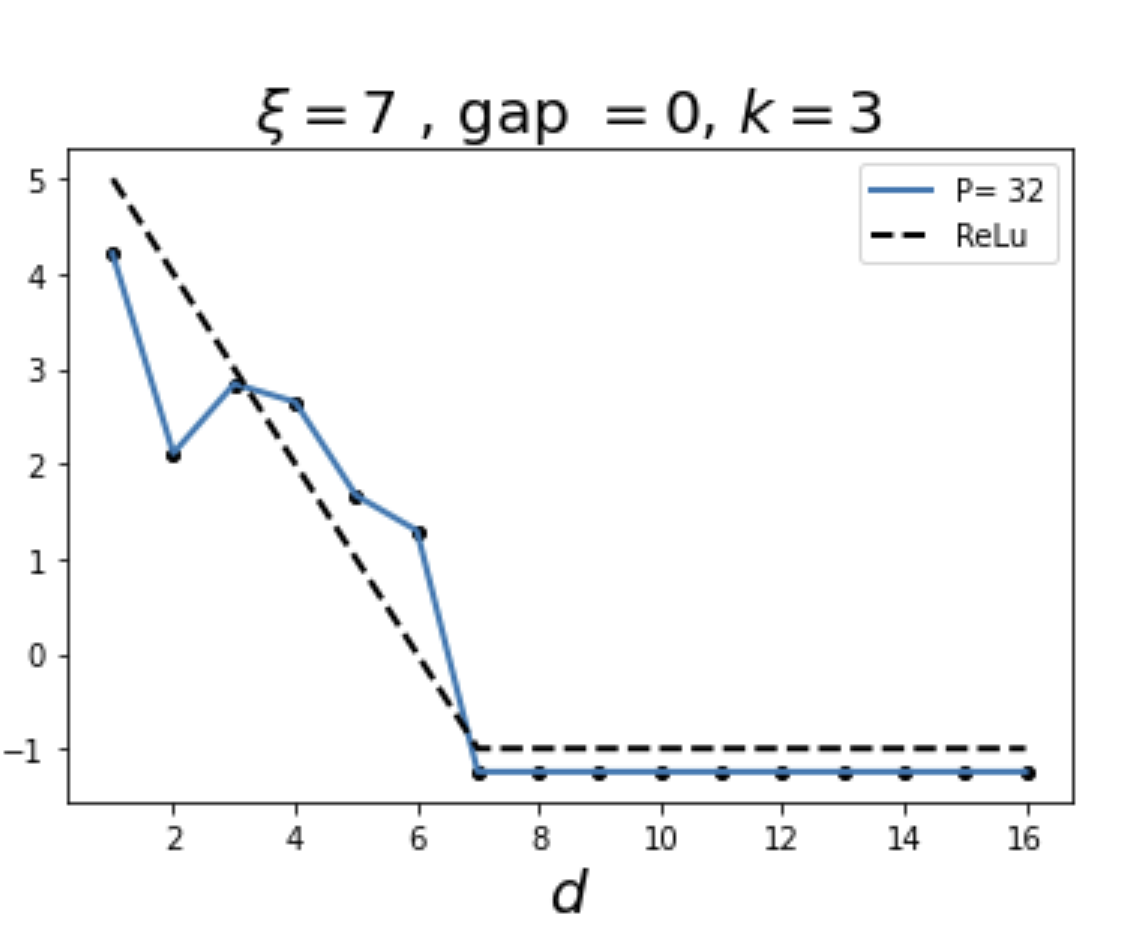
-1

Solution 1: high-frequency filters 1/2

Input

Layer 1,

3 channels

For layers $k<\tilde{k}$: as above.

Layer $\tilde{k}$

-1 bias

Sign of positive interference!

Output: $f_p(x)=f_p(d)=\text{ReLu}(\xi-d)$

-1

Solution 1: high-frequency filters 2/2

Computing stability to diffeo

What does a diffeo $\tau$ do here?

Prob 1/3

D_{f_p} =\frac{\langle (f_p(\tau(x))-f_p(x))^2\rangle}{\langle (f_p(x_1)-f_p(x_2))^2\rangle}

Goal:

compute stability to diffeo for the output and internal layer representation

Do the proposed solutions capture CNN solution?

The filters seem are high freq at layer 1.

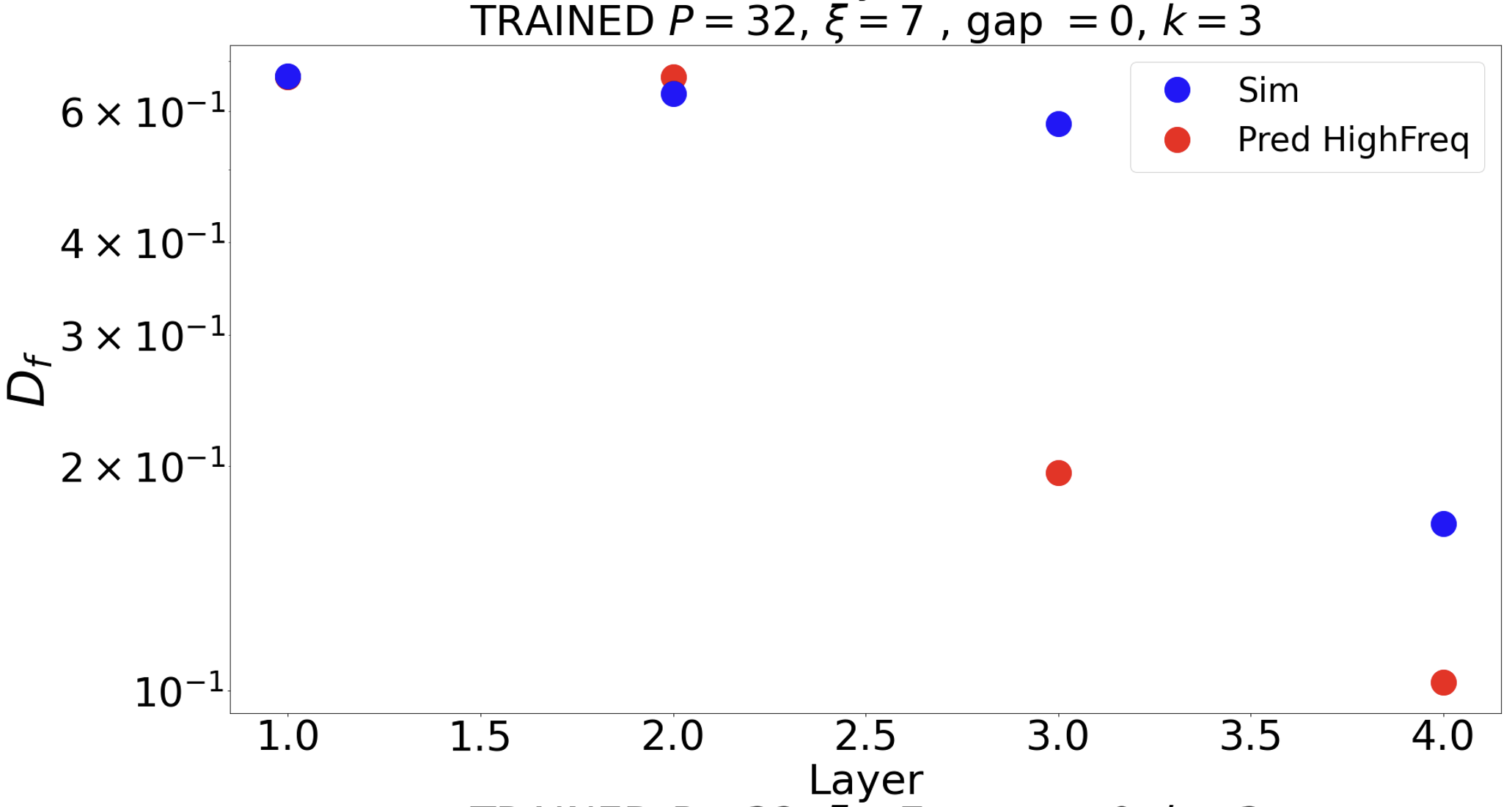
Computing stability to noise

What does adding noise $\eta$ do here?

G_{f_p} =\frac{\langle (f_p(x+\eta)-f_p(x))^2\rangle}{\langle (f_p(x_1)-f_p(x_2))^2\rangle}

Goal:

compute stability to noise for the output and internal layer representation

\eta_{i-1}

\eta_{i}

\eta_{i+1}

where $\eta_i$ are $l$ indipendent and identically distributed gaussian noises with mean 0 and standard deviation $\sigma$ such that:

l\sigma^2 \sim \langle (\tau(x)-x)^2\rangle = 8/3

Do the proposed solutions capture CNN solution?

The filters seem are high freq at layer 1.

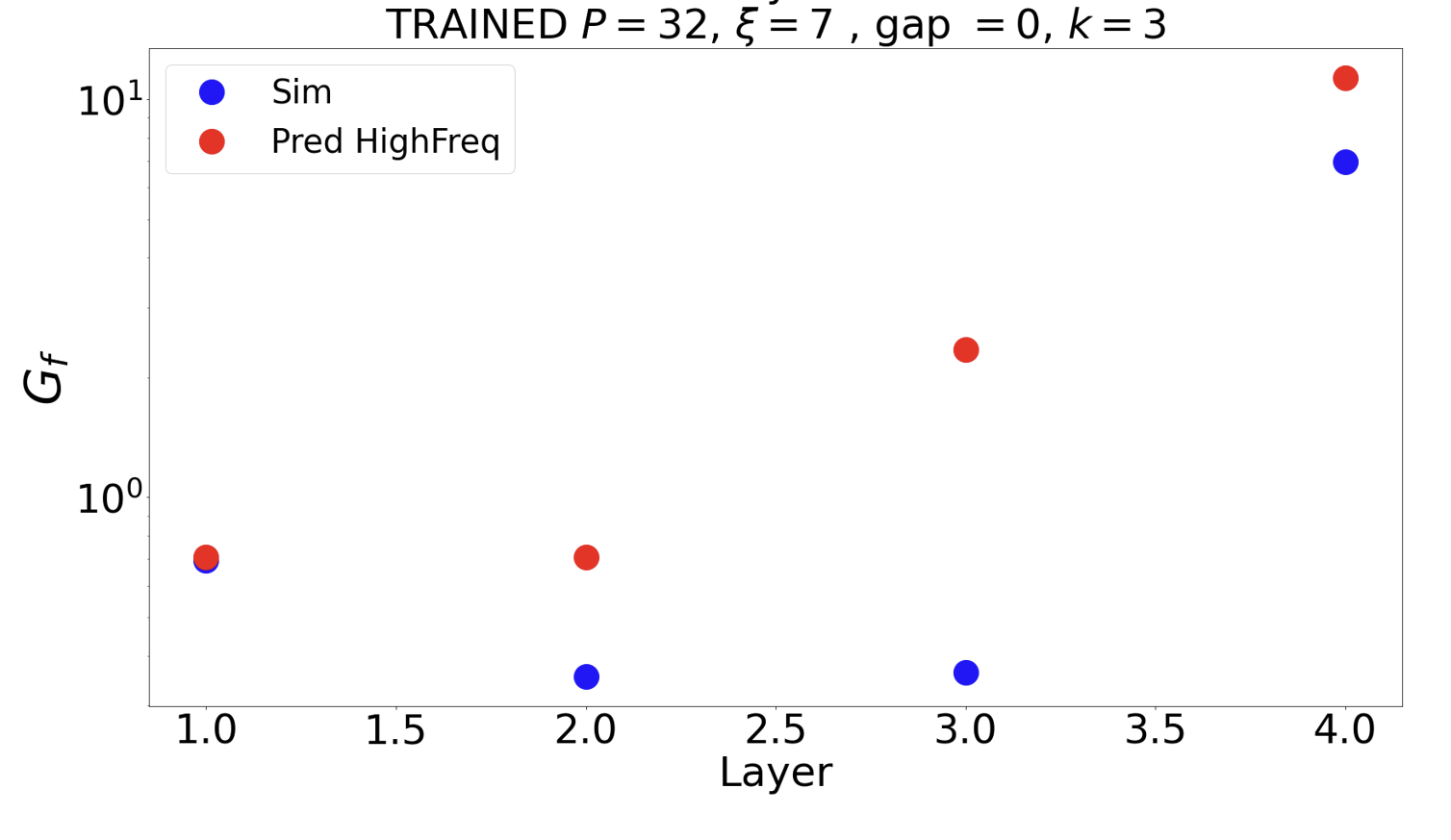
Conclusions (theoretical part)

To do: check the robustness of the result (vary number of channels and $\xi$ )
To do: check if we can do better for internal layers >1.
Once we find the solution, it would show how adaptive pooling is built within the CNN to recognize $\xi$.

the role of adaptive pooling

Learning in convolutional neural networks:

The puzzling success of deep learning

the curse of dimensionality

Invariances give structure to data-space

Measuring deformation invariance

Measuring deformation invariance

Measuring deformation invariance

Measuring deformation invariance

Relative stability to diffeomorphisms

Relative stability to diffeomorphisms remarkably correlates to performance!

Outline

A spherically symmetric dataset

A spherically symmetric dataset

A spherically symmetric dataset

A spherically symmetric dataset to gain insights on real images

Lazy vs. feature performance in the spherical model

To recap:

The spherical model rationalizes real-data findings

Outline

CNNs building block: the convolutional layer

A convolutional neural network:

Which parts of the network give relative stability?

Which operations give relative stability to diffeo?

Disentangling spatial and channel pooling in DNNs

Additional evidence for filter pooling:

A data model for filter pooling

A model for filter pooling

data-points \(x_\mu\in \mathbb{R}^{d\times d}\)

labels \(y_\mu\)

data-set \(\{x_\mu, y_\mu\}\)

Adaptive pooling model can reproduce real-data obervations

Can we build a theory for the adaptive pooling model to rationalize real-data findings?

Outline

A simple convolutional network 1/2

A simple convolutional network 2/2

Our strategy

Solution 1: low-frequency filters 1/2

Solution 1: low-frequency filters 2/2

Solution 1: high-frequency filters 1/2

Solution 1: high-frequency filters 2/2

Computing stability to diffeo

Do the proposed solutions capture CNN solution?

The filters seem are high freq at layer 1.

Computing stability to noise

Do the proposed solutions capture CNN solution?

The filters seem are high freq at layer 1.

Conclusions (theoretical part)