Relative stability toward diffeomorphisms indicates performance in deep nets

Leonardo Petrini, Alessandro Favero, Mario Geiger, Matthieu Wyart

Physics of Complex Systems Lab, EPFL

Introduction

The puzzling success of deep learning

Deep learning is incredibly successful in wide variety of tasks

Curse of dimensionality when learning in high-dimension,
in a generic setting

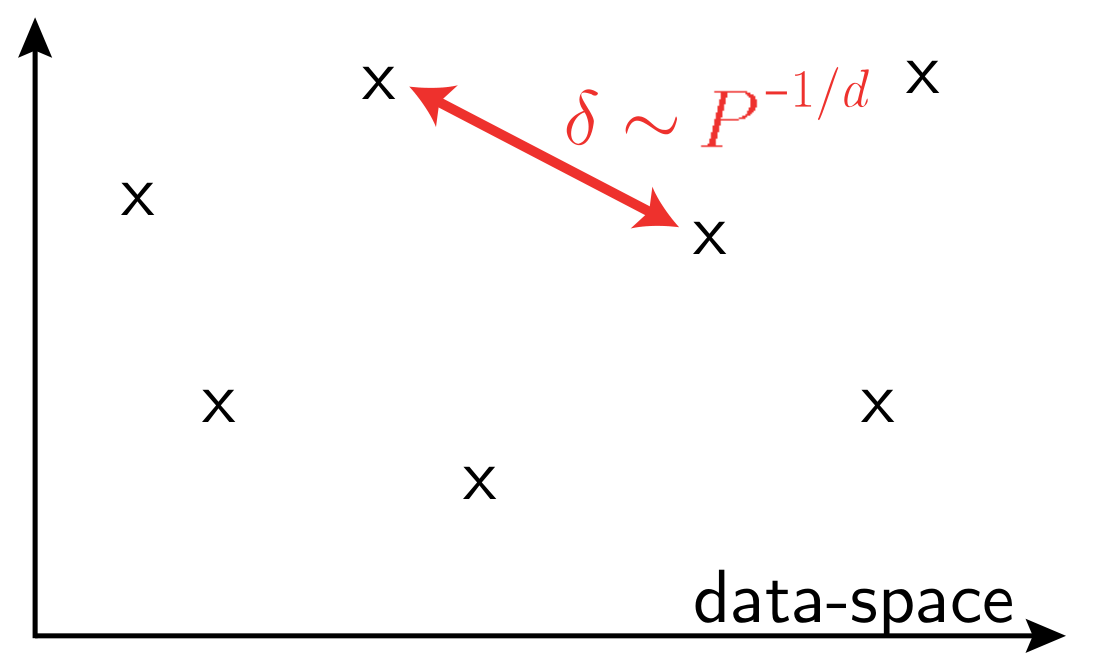
vs.

In high dimension, data that have little structure cannot be learned

$P$: training set size

$d$ data-space dimension

What is the structure of real data?

Cat

Idea: there are directions in input space that the task is invariant to.
An example is the space of image translations - that is small though.
Space of smooth deformations is much larger - getting invariant to that can be key to escape the curse of dimensionality!
Such invariance can be characterized by the stability:
Hypothesis: nets perform better and better by becoming more and more stable to diffeo

Invariances give structure to data-space

Bruna and Mallat (2013), Mallat (2016), ...

\tau x

\tau

$S = \frac{\|f(x) - f(\tau x)\|}{\|\nabla\tau\|}$

$f$ : network function

Is it true or not?

Can we test it?

$x-$translations

$y-$translations

Introduce a max-entropy distribution of diffeomorphisms of controlled magnitude
Define the relative stability toward diffeomorphisms with respect to that of a random transformation, $R_f$

Our contribution:

Stability to fixed-norm random transformations

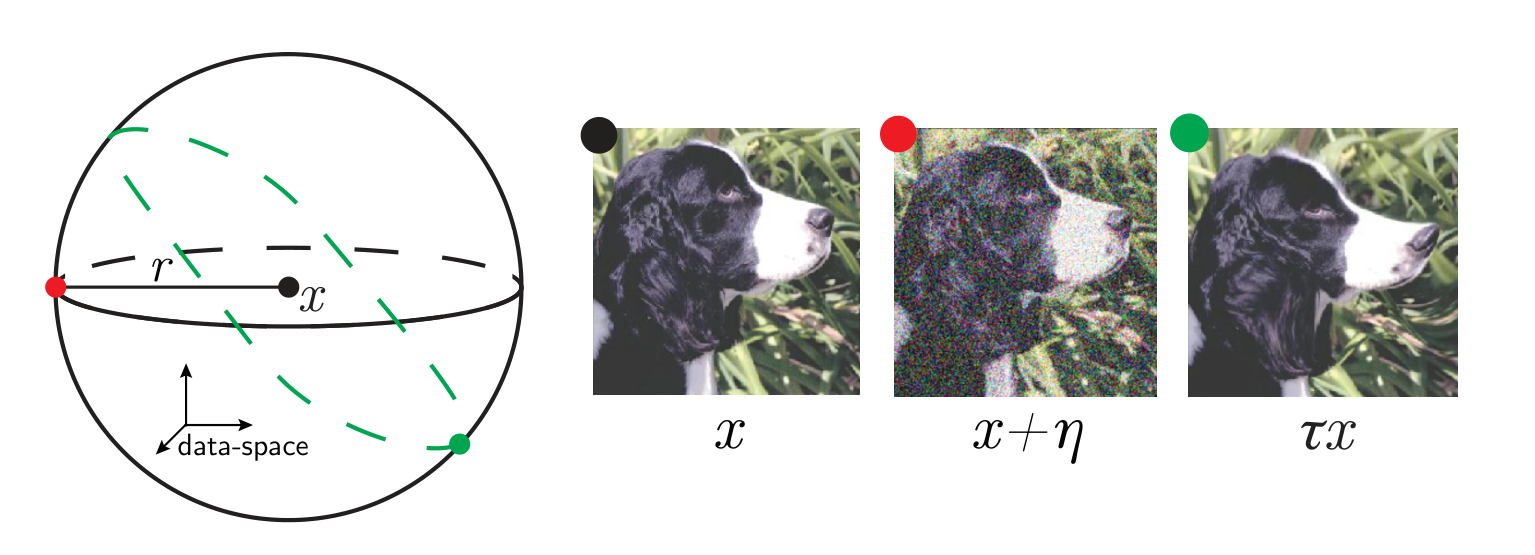
We sample uniformly random transformations of a given norm
Stability with respect to a generic random transformation $\|f(x) - f(x + \eta)\|^2$
vary a lot with training and among different nets (usually better nets are less stable)
To understand diffeomorphism invariance one needs to define stability in relative terms!

Relative stability to diffeomorphisms

$x$ input image

$\tau$ smooth deformation

$\eta$ isotropic noise with $\|\eta\| = \langle\|\tau x - x\|\rangle$

$f$ network function

Observable that quantifies if a deep net is less sensitive to diffeomorphisms than to generic data transformations

$$R_f = \frac{\langle \|f(x) - f(\tau x)\|^2\rangle_{x, \tau}}{\langle \|f(x) - f(x + \eta)\|^2\rangle_{x, \eta}}$$

Relative stability:

Introduce a max-entropy distribution of diffeomorphisms of controlled magnitude
Define the relative stability toward diffeomorphisms with respect to that of a random transformation, $R_f$
Keys results: $R_f$ is learned and indicates performance!

Our contribution:

Good deep nets learn to become relatively stable

$$R_f = \frac{\langle \|f(\tau x) - f(x)\|^2\rangle_{x, \tau}}{\langle \|f(x + \eta) - f(x)\|^2\rangle_{x, \eta}}$$

Results:

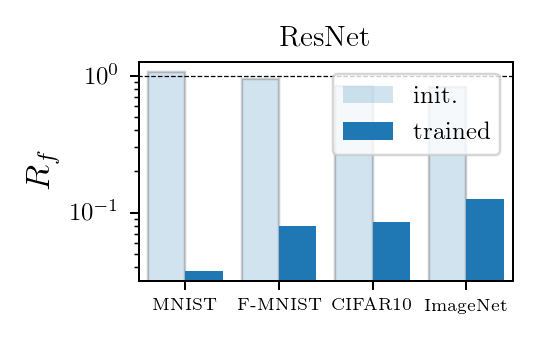
At initialization (shaded bars) $R_f \approx 1$ - SOTA nets don't show stability to diffeo at initialization.
After training (full bars) $R_f$ is reduced by one/two orders of magnitude consistently across datasets and SOTA architectures.
By contrast, (2.) doesn't hold true for fully connected and simple CNNs for which $R_f \sim 1$ before and after training.

Deep nets learn to become stable to diffeomosphisms!

Relation with performance?

Relative stability to diffeomorphisms remarkably correlates to performance!

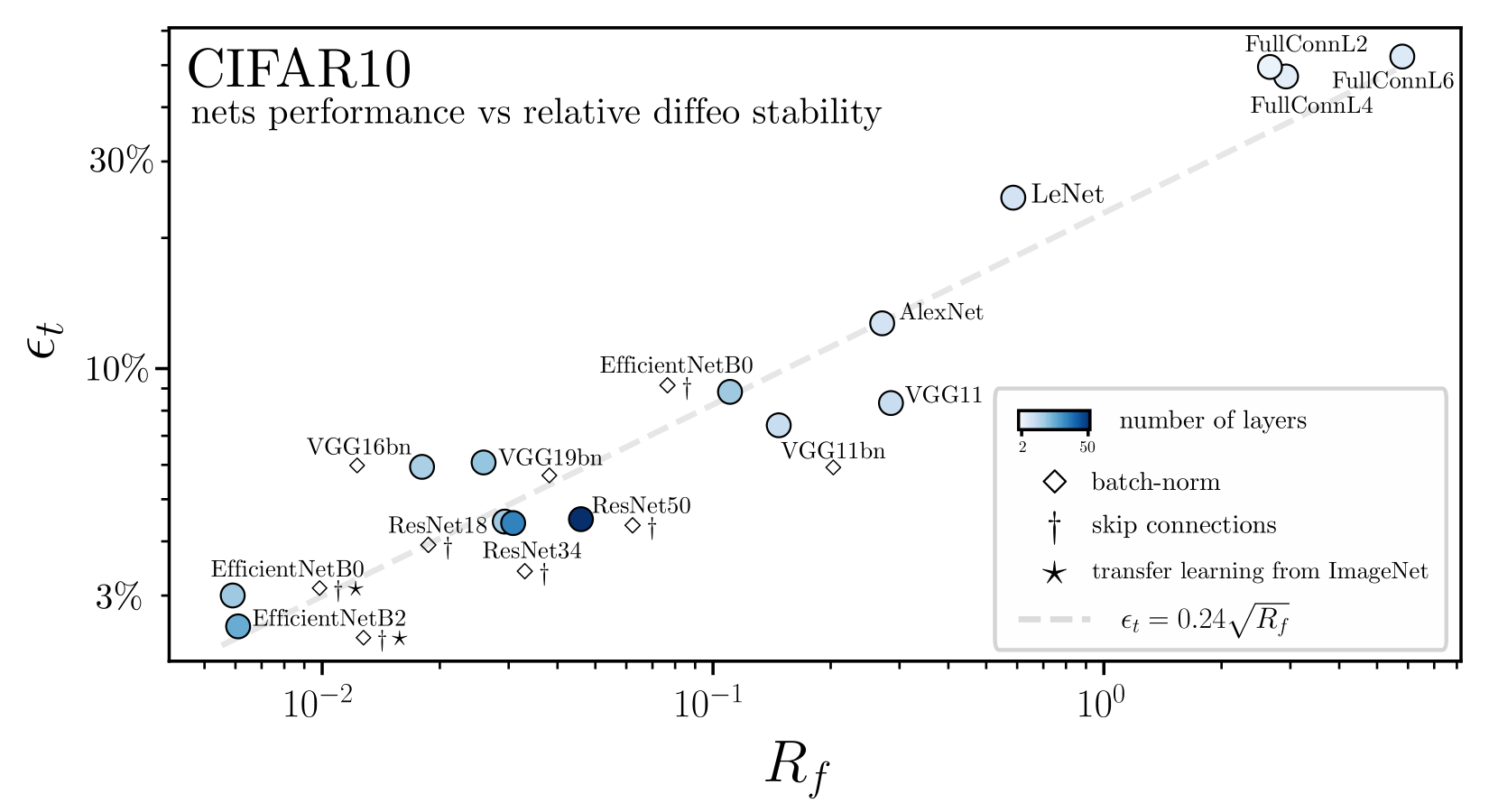
1. How to rationalize this behavior?

2. How do CNNs build diffeo stability and perform well?

conclusions

Introduced max-entropy distribution of diffeomorphisms
Key idea: relative stability is the relevant observable, instead of just stability considered in the past
Main finding: relative stability correlates to performance
Can do data augmentation with max-entropy diffeo!
What does this tell us about adversarial robustness?
By which mechanism NNs learn the invariance?
Quantitively relate performance and relative stability $\rightarrow$ model design?

future work

slides.com/leopetrini

Thanks!