數據分析
Lecturer:
建北電資小設課運算思維 Lesson 2
I swear,我原本想要用上堂課的模板來做這個簡報,但那個背景亮哭我ㄌ
一維數據分析
aka 泥悶得仙貝芝士!
算術平均數
設一組\(n\)個數據 \(x_1, x_2, x_3,..., x_n\) ,則
算術平均數 \( \mu = \frac{1}{n} \displaystyle \sum_{i=1}^{n} x_i\)
超級簡單對吧,只是我不知道你們還習不習慣\(\sum\)的寫法就是了
加權平均數
設一組\(n\)個數據 \(x_1, x_2, x_3,..., x_n\)
加權平均數\(w = \frac{\displaystyle \sum_{i=1}^{n} x_iw_i}{\displaystyle \sum_{i=1}^{n} w_i}\)
同樣也能理解對吧,算段考平均成績的時候可以用到ㄛ
且分別對應權數\(w_1, w_2, w_3,...,w_n\),則
幾何平均數
設一組皆為正數的\(n\)個數據 \(x_1, x_2, x_3,..., x_n\),則
\( = \sqrt[n]{\displaystyle \prod_{i=1}^{n} x_i}\)
如果這組資料的數字是有相乘性質的,
那我們就應該要使用幾何平均數!
如:利率等。
加權平均數
非常小小的例題
以下是運算思維講師之一 rainple0130 這次段考的各科成績。請聰明的你來幫幫他算出他這次段考的加權平均分數ㄅ :partying_face:
| 科目 | 成績 | 學分 |
|---|---|---|
| 國文 | 77 | 4.0 |
| 數學 | 72 | 4.0 |
| 英文 | 65 | 4.0 |
| 物理 | 86 | 3.0 |
| 化學 | 70 | 3.0 |
| 歷史 | 82 | 2.0 |
ans: 74.4分 (吧

一塊地毯在印度原產地賣給當地集貨商時是成本的\(6\)倍,集貨商賣給外銷商是其成本的\(4\)倍,外銷商賣給美國的進口商是其成本的\(3\)倍,而進口商賣給當地的大賣店是成本的\(3\)倍,大賣店賣給零售商則是其成本的\(2\)倍。試問平均每一經手者賣出價錢是其成本的幾倍?
[ 北一學資第二冊第二章數據分析 P.32 B部分第一題 ]
(若有必要,請使用計算機。)
不要問我怎麼拿到的w
ans: 約3.37倍
非常小小的例題

眾數 & 全距
眾數:一組數據中出現最多次的東東
全距:一組數據中最大與最小數之差
中位數
將一組\(n\)個數據由小排到大後,
(1)若\(n\)是奇數:令\(k = \frac{n+1}{2}\),則中位數為\(x_k\)
(2)若\(n\)是偶數:令\(k = \frac{n}{2}\),則中位數為\(\frac{x_k+x_{k+1}}{2}\)
百分位數
將一組\(n\)個數據由小排到大後,定義第\(k\)百分位數\(P_k\)為:
(1)若\(n\times\frac{k}{100}\)為整數:
令\(m = n\times\frac{k}{100}\),則\(P_m = \frac{x_m+x_{m+1}}{2}\)
(2)若\(n\times\frac{k}{100}\)是非整數:
類推適用w (好我不知道我在說什麼
令\(m = (n\times\frac{k}{100}\)無條件進入到整數位),則\(P_m=\frac{x_m+x_{m+1}}{2}\)
四分位數
第一四分位數為\(Q_1 = P_{25}\)
第二四分位數為\(Q_2 = P_{50}\)
第三四分位數為\(Q_3 = P_{75}\)
呈上頁,第\(k\)百分位數為\(P_k\)
很小的練習
一組數據\(22, 25, 29, 29, 25, 26, a, b, c\),已知眾數是\(29\),中位數是\(28\),算術平均數是\(27\),且\(a > b > c\)),求\(a\)。
ans: 30
很小的練習
在九年級的籃球比賽中,925 班進行班級的自主練習。導師將全班同學人數平分成甲、乙兩組。因為乙組的身高太矮,所以將原本甲組\(5\)為平均身高為\(165\)公分的同學調到乙組,再將乙組\(5\)位平均身高為\(153\)公分的同學調到甲組,結果乙組後來的平均身高增加\(3\)公分。試求全班人數?
ans: 40人
一維數據分析
但試試你們沒學過的,吧
離均差:\(x_i - \mu_x\)
變異數\(\sigma^2\)
變異數:所有離均差的平方和的平均
於是事情開始變麻煩ㄌ...
變異數\( \sum^2 = \displaystyle \frac{1}{n} \sum_{i=1}^{n} (x_i-\mu_x)^2 = \frac{1}{n} \sum_{i=1}^{n} x_i^2 - \mu_x^2\)
知道怎麼證明ㄇ(?
變異數\( \sum^2 = \displaystyle \frac{1}{n} \sum_{i=1}^{n} (x_i-\mu_x)^2\)
標準差\(\sigma\)
剛剛的變異數取正平方根而已la
母體標準差\(\sigma = \sqrt{\frac{1}{n}\displaystyle\sum_{i=1}^{n} (x_i-\mu_x)^2} = \sqrt{\frac{1}{n}\displaystyle\sum_{i=1}^{n} x_i^2 - \mu_x^2}\)
樣本標準差\(\sigma = \sqrt{\frac{1}{n-1}\displaystyle\sum_{i=1}^{n} (x_i-\mu_x)^2}\)
非常小小的例題 :thonk:
酥育根很在意他的體態,習慣在起床後站上電子體重機五次,重複地量測體重。以下是他在某個早上的測量數據:
| 測量次數 | 第一次 | 第二次 | 第三次 | 第四次 | 第五次 |
|---|---|---|---|---|---|
| 體重(kg) | 49.9 | 50.1 | 50.0 | 50.1 | 49.9 |
ans: 0.1kg
根據上面的數據,試求出酥育根體重的標準差?
數據的線性變換
針對一組數據\(x_1, x_2, x_3,...,x_n\)進行線性變換,即\(y_i = ax_i + b\),則:
- \(\mu_y = a\mu_x + b\)
- \(\sigma_y = |a|\sigma_x\)
標準化分數(\(z\)分數)
設一組\(n\)個數據\(x_1, x_2, x_3,...,x_n\)的算術平均數為\(\mu_x\),標準差為\(\sigma_x\),則規定
標準化分數\(x_i' = \frac{x_i - \mu_x}{\sigma_x}\)
標準化分數(\(z\)分數)的性質
(1)\(z_1', z_2', z_3',...,z_n'\)的算術平均數為0
這些性質會證明ㄇ(?
(2)\(z_1', z_2', z_3',...,z_n'\)的標準差為1
(3)\(\displaystyle\sum_{i=1}^{n} x_i'^2 = n\)
某次段考後,多數同學成績偏低,因此決定將每人的原始成績取平方根再乘以\(10\)作為正式紀錄。今\(100\)位同學,發現調整後的平均為\(55\)分,標準差為\(20\)分,求這\(100\)位同學未調整前的平均數。
ans: 34.25分
小小練習

設\(f(x) = \displaystyle\sum_{i=1}^{n} (x_i - x)^2\),
則其在 \(x = \mu_x\),也就是\(x\)是所有\(x_i\)的算術平均數時有最小值。
快速穿插小觀念 :thonk:
\(f(x) = \displaystyle\sum_{i=1}^{n} (x_i - x)^2 \\ = \displaystyle\sum_{i=1}^{n} ({x_i}^2 - 2{x_i}{x} + x^2) \\ = \displaystyle\sum_{i=1}^{n} {x_i}^2 - 2x \displaystyle\sum_{i=1}^{n} x_i + \displaystyle\sum_{i=1}^{n} x^2 \\ \)
\( \displaystyle\sum_{i=1}^{n} x^2 - 2x\displaystyle\sum_{i=1}^{n} x_i \\ = nx^2 - 2xn\mu_{x_i} \\ = n(x^2 - 2x\mu_{x_i} + {\mu_{x_i}}^2) \\ = n(x - \mu_{x_i})^2\)
所以 \(x = \mu_{x_i} \),也就是算術平均數時有最小值!
有\(10\)名學生的數學考科及分數分別為\(x_1\),\(x_2\),\(x_3\),...,\(x_{10}\),其算術平均數為\(8\)分,標準差為\(2\)分。若令\(f(x)=(x_1-x)^2+(x_2-x)^2+...+(x_{10}-x)^2\),請選出正確的選項。
(1) \(f(8)=20\)
(2) \(f(8)=40\)
(3) \({x_1}^2+{x_2}^2+...+{x_{10}}^2=680\)
(4) \(f(7)<f(8)\)
(5) \(f(8)<f(9)\)
ans: 2, 3, 5
小小練習

假設有\(n\)個數據成等差數列,且其公差為\(\sqrt{\frac{2}{3}}\),若此資料的變異數為\(231\),求\(n\)之值。
p.s. 為方便計算,可討論\(n\)為奇數的情況即可。
ans: 43
挑戰題 (嗎

可是他被歸類在 A 部分 :thonk:
二維數據分析 --- 相關係數
相關係數
設一組\(n\)個數據 \((x_1, y_1), (x_2, y_2), (x_3, y_3),...,(x_n,y_n)\)
將這些數據標準化為\((x_1', y_1'),(x_2', y_2'), (x_3', y_3'),..., (x_n', y_n')\),則
定義相關係數\(r = \frac{\Sigma_{i=1}^{n} x_i'y_i'}{n}\)
我ㄉ數據沒有標準化怎麼辦
我們現在定義三ㄍ咚咚:
\(S_{XX} = \displaystyle\sum_{i=1}^{n} x_i^2 - n\mu_x^2\)
\(S_{YY} = \displaystyle\sum_{i=1}^{n} y_i^2 - n\mu_y^2\)
\(S_{XY} = \displaystyle\sum_{i=1}^{n} x_iy_i - n\mu_x\mu_y\)
\(S_{XX} = \displaystyle\sum_{i=1}^{n} x_i^2 - n\mu_x^2 = n\sigma_x^2\)
\(S_{YY} = \displaystyle\sum_{i=1}^{n} y_i^2 - n\mu_y^2 = n\sigma_y^2\)
我ㄉ數據沒有標準化怎麼辦
定義相關係數\(r = \frac{S_{XY}}{\sqrt{S_{XX}}\sqrt{S_{YY}}}\)
有被一堆式子搞得暈頭轉向了ㄇ
定義相關係數
\(r = \frac{S_{XY}}{\sqrt{S_{XX}}\sqrt{S_{YY}}} = \frac{\displaystyle\sum_{i=0}^{n} (x_i - \mu_x)(y_i - \mu_y)}{n\sigma_x\sigma_y}\)
相關係數\(r\)的意義
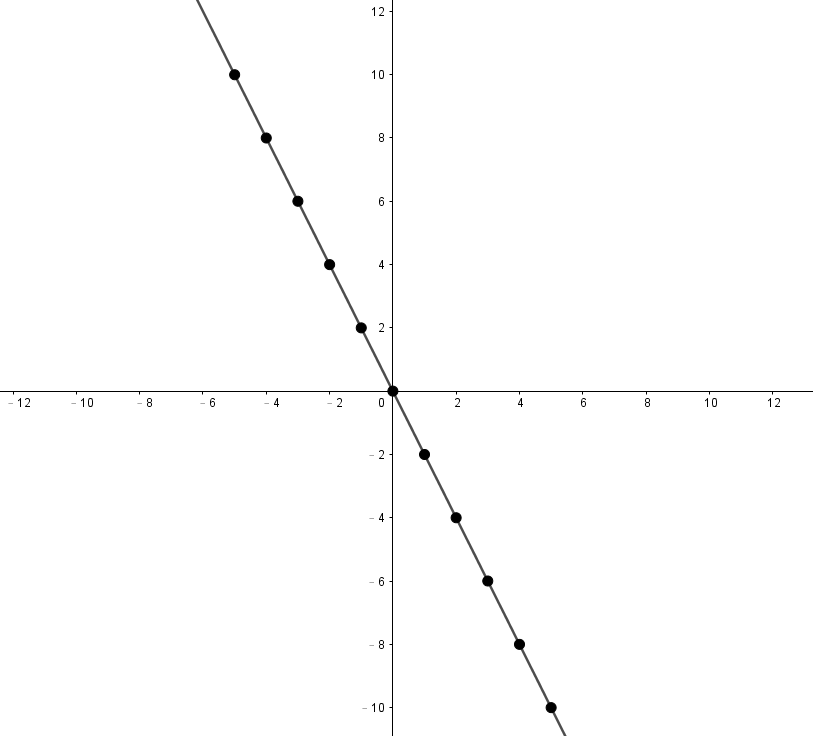
\(r = -1\):
完全負相關
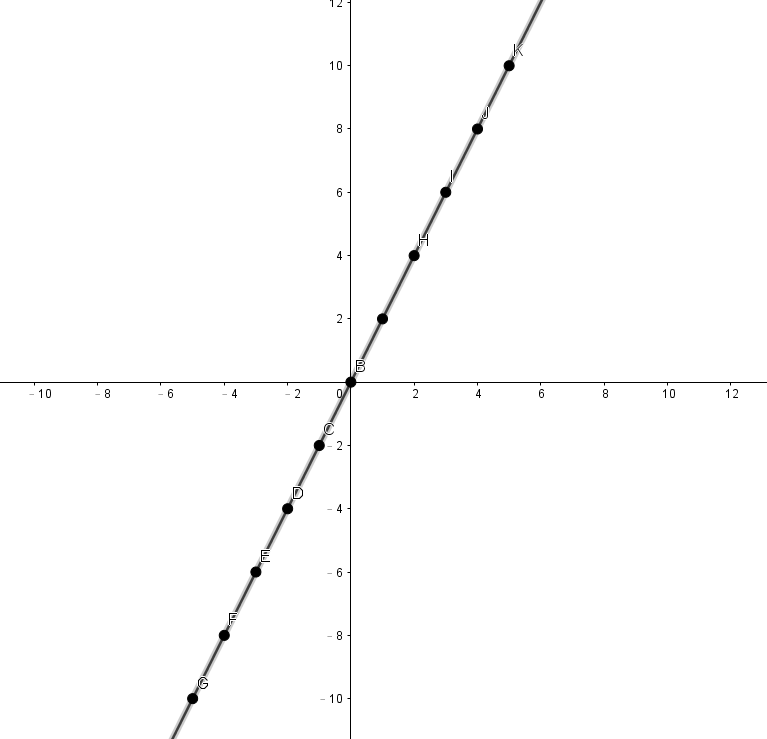
\(r = 1\):
完全正相關
相關係數\(r\)的意義
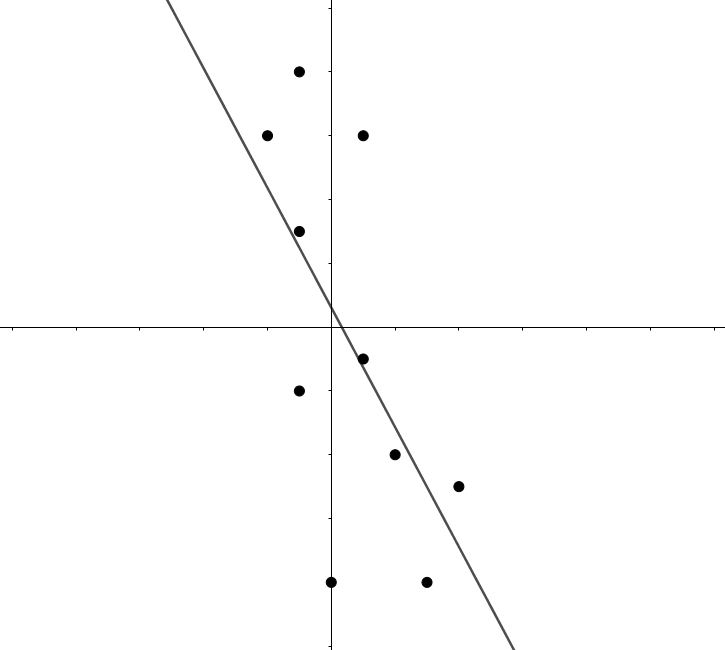
\(-1 < r < 0\):
負相關
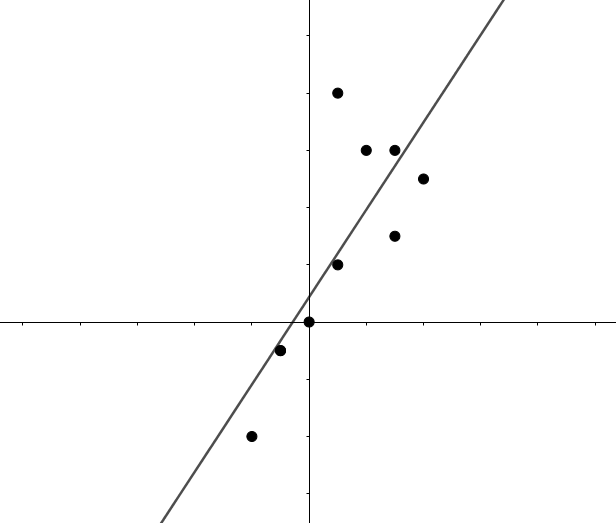
\(0 < r < 1\):
正相關
相關係數\(r\)的意義
\(r = 0\):零相關
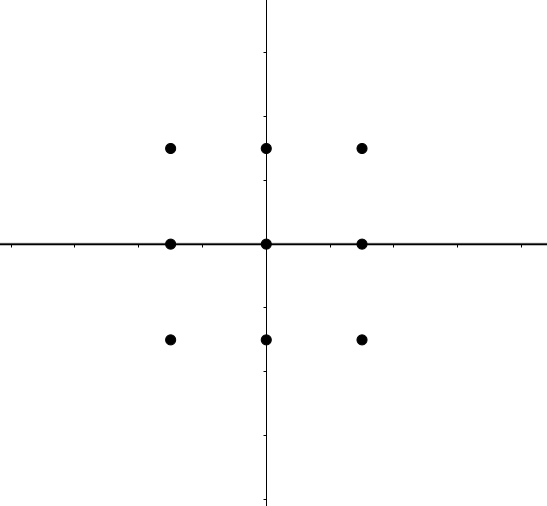
成立於當所有點所形成的圖形呈線對稱
相關係數\(r\)的性質
- \(-1\leq r \leq 1\)
- 令\(X\)與\(Y\)的相關係數為\(r_{(X,Y)}\),則\(r_{(X,Y)} = r_{(Y,X)}\)
- 設\(X' = aX+b, Y' = cX+d\),則:
當\(ac>0\)時,\(r_{(X',Y')} = r_{(X,Y)}\)
當\(ac<0\)時,\(r_{(X',Y')} = -r_{(X,Y)}\)
五位同學在某次定期考中,國文與英文的成績分別如下:
ans: 0.4
小練習

| 國文成績x | 英文成績y | |
|---|---|---|
| 章程一 | 84 | 70 |
| 格列格里七世 | 90 | 75 |
| シエスタ大好き | 87 | 90 |
| 米斯塔 | 96 | 85 |
| E | 93 | 80 |
求這五位同學兩科成績的相關係數。
令\(X\)代表每個高中生平均每天研讀數學的時間(以小時計),則\(W = 7(24-X)\)代表每個高中生平均每週花在研讀數學以外的時間。令\(Y\)代表每個高中生數學學科能力測驗的成績。設\(X, Y\)之相關係數為\(0.83\),求\(w, Y\)之相關係數。
ans: -0.83
小練習

二維數據分析 --- 回歸直線
what is 回歸直線
生出一組數據,把它變成散佈圖,
然後我們試圖找到一條距離這些點最近的理想直線
就是鼎鼎大名的回歸直線ㄌ🤤
正式的定義,還有我們具體要怎麼求出的部分ㄋ(?
尋找回歸直線 --- 最小平方法
設一組\(n\)個數據\((x_1,y_1), (x_2,y_2), (x_3,y_3),...,(x_n,y_n)\),
且\(y\)對\(x\)(即要從x來推測y的數值)的回歸直線為\(y=ax+b\)
我們從平面座標上各點做垂直線到\(y=ax+b\)
可以發現,這個線段的距離是\(|y_i - (ax+b)|\)
所以所有的點分別作垂直線到回歸直線的總距離為
\(\Sigma_{i=1}^{n} |y_i -(ax+b)|\)
所以我們找出這個咚咚的最小值就好了...ㄇ?
絕對值超級難算ㄟ
尋找回歸直線 --- 最小平方法
人們的解決方法:改成求這些距離的平方和,就輕鬆解決啦~
於是我們現在要求的是:
\(\Sigma_{i=1}^{n} (y_i - (ax+b))^2\)的最小值
怎麼做呢? 土法煉鋼
尋找回歸直線 --- 最小平方法
我們直接來個實例
設\(5\)個二維數據為:
| X | -2 | -1 | 0 | 1 | 2 |
|---|---|---|---|---|---|
| Y | 0 | 0 | 1 | 1 | 3 |
利用最小平方法,求\(Y\)對\(X\)的最適直線方程式。
ans: \(y=\frac{7}{10}x + 1\)
尋找回歸直線 --- 最小平方法
怎麼做呢?
設回歸直線為\(y=a+bx\)
則所求\(D = \Sigma_{i=1}^{5} (y_i - a - bx_i)^2)\)
\(= (0-a+2b)^2 + (0-a+b)^2 + ... +(3-a-2b)^2\)
\(= 5a^2 + 10b^2 -10a - 14b +11\)
\(= 5(a-1)^2 + 10(b-\frac{7}{10})^2 + \frac{11}{10}\)
由此可知,當\(a = 1, b = \frac{7}{10}\)時,所求\(D\)有最小值\(\frac{11}{10}\)
所以我們的回歸直線就是\(y = \frac{7}{10}x + 1\)
尋找回歸直線 --- 相關係數(?
很多數據怎麼辦?
我們的相關係數\(r\)派上用場ㄌ!
一組標準化數據的回歸直線為:\(y' = rx'\)
也就是說...
(1)標準化數據的回歸直線必通過\((0,0)\)
(2)標準化數據的回歸直線斜率為\(r\)
尋找回歸直線 --- 相關係數(?
一組標準化數據的回歸直線為:\(y' = rx'\)
以\(x' = \frac{x_i - \mu_x}{\sigma_x}, y' = \frac{y_i - \mu_y}{\sigma_y}\)代入
可以發現\(y - \mu_y = m(x - \mu_x)\)
而回歸直線必通過\((\mu_x, \mu_y)\)
其中,斜率\(m = r \cdot \frac{\sigma_y}{\sigma_x} = \frac{S_{XY}}{S_{XX}} \)
你還醒著ㄇw
已知\(X\)與\(Y\)的二維數據\((x_i, y_i), i = 1, 2, ..., 5\),如下表所示
ans: (1) 0.8 (2) \(y = 0.8x\)
小練習

| X | 34 | 25 | 28 | 16 | 22 |
|---|---|---|---|---|---|
| Y | 15 | 13 | 19 | 7 | 11 |
標準化得\(X'\)與\(Y'\)的二維數據\((x_i, y_i)\),其中\(x_i' = \frac{x_i-\mu_x}{\sigma_x}\),\(y_i' = \frac{y_i-\mu_y}{\sigma_y}\),\(i = 1, 2, ..., 5\),求:
(1) \(X'\)與\(Y'\)的相關係數。
(2) \(Y'\)對\(X'\)的最適直線方程式
設二組數據\(x_1, x_2, ..., x_{10}\)與\(y_1, y_2, ..., y_{10}\),\(x_1+x_2+...+x_10=140\),\(y_1+y_2+..+y_10=1300\),\({x_1}^2+{x_2}^+...+{x_{10}}^2 = 2528\),\({y_1}^2+{y_2}^2+...+{y_{10}}^2 = 184730\),\(x_1y_1 + x_2y_2 + ... + x_{10}y_{10} = 21040\),利用最適直線,預測若\(x\)之值為\(25\),\(y\)之值。
ans: 185
挑戰題 (吧
