基礎數學

Jul. 5 @ 北一女中

哈嘍各位！！！

https://rb.gy/zhpbpo

臺上的老人是誰？

劉至軒
建中數資 \(\rightarrow\) ~~臺大資工~~ 伊利諾大學香檳分院（UIUC）
2020 北市賽一等獎、全國賽三等獎
2019、2020 TOI 一階結訓
2022 ICPC 北美賽區 Rk. 15、晉級 WF

講師沒有進過二階 ;-;

正式課程前⋯⋯

假設各位的高中數學都會了，沒什麼競賽經驗
因為有些東西同學可能還沒學到，請不要吝嗇於舉手發問發問發問！
絕對不可能只有妳/你有這個問題的！！！
課程中將有一些例題，有什麼想法請儘量發言！
這次上課的題單
道歉聲明：因為時間不足，所以（大）一（部）些（分）證明可能省略或草草帶過，請用心體會數學之玄妙（X

很重要所以寫三遍

今天會學到什麼

Number Theory

Combinatorics

Fun Stuff

數論

排列組合

好玩的東西

希望⋯⋯

三個小時實在太短了 ;(
所以這會是一個走馬看花的行程
沒有馬上搞懂很正常！！！
gl & hf :D

趴萬 —— 數論

Number Theory

數論是什麼？

研究整數的學科
在這個部分當中，只要提到數字指的就是整數！！
- 暫時不考慮非整數的有理數、實數、複數等
接下來會看到吐的關鍵字：質數、同餘、歐拉

數字與它們的關係

Numbers and their relations

國小複習 + 名詞定義

若存在一個數字 \(q\) 使得 \(a = qb\)，則：
- \(a\) 是 \(b\) 的倍數
- \(b\) 是 \(a\) 的因數
- 亦寫作 \(b | a\)
- \(0\) 是所有數字的倍數，但不是任何數字的倍數
- \(\forall k, a | b \iff a | b + ka\)（為什麼？）
Ex.
- \(2 | 0\)、\(2 | 4\)、\(2 \not| 3\)、\(2 | (-2)\)

最大公因數 / 最小公倍數

相信大家國中小的數學都學的非常好
這裡只是一些定義而已！
定義 \(a, b\) 的最大公因數為最大的數字 \(m\) 使得 \(m | a\) 且 \(m | b\)，記為 \(\gcd(a, b)\)。
定義 \(a, b\) 的最小公倍數為最小的數字 \(n\) 使得 \(a | n\) 且 \(b | n\)，記為 \(\textrm{lcm}(a, b)\)。
小知識：\(ab = \gcd(a, b) \cdot \textrm{lcm}(a, b)\)

輾轉相除法

\(\gcd(x, 0) = \gcd(0, x) = x\)
\(\gcd(a, b) = \gcd(a - b, b)\)
\(\implies \gcd(a, b) = \gcd(b \% a, a)\)
一直跑直到其中一個滿足第一式就回傳另外一個
\(O(\log \min(a, b))\)

int gcd(int a, int b) {
    return !b ? a : gcd(b, a % b);
    // 好耶 一行就寫完了
}

std::gcd(int a, int b); //C++ 17

同餘

就是「取餘數」！兩個數字 \(a\)、\(b\) 模 \(m\) 同餘若它們兩個除以 \(m\) 有相同的餘數
寫作 \(a \equiv b \pmod{m}\)
\(a\) 除 \(b\) 的餘數記作 \(a\%b\) （C++寫法）
數學式：

\(a \equiv b \pmod{m} \iff m | (a - b)\)

mod 12

mod 24

同餘的運算明星三缺一

\(a \equiv b \pmod{m} \iff a \pm c \equiv b \pm c \pmod{m}\)
\(a \equiv b \pmod{m} \iff ac \equiv bc \pmod{m}\)
除法怎麼辦？
\(15 \cdot 2 \equiv 20\cdot 2 \pmod{10}\) 但除 \(2\) 就不對了???
模逆元！

why?

乘法模擬元

模 \(N\) 底下，一個數字 \(x\) 的模擬元（若存在）定義為最小的正整數 \(y\) 使得 \(xy \equiv 1 \pmod{N}\)
正常的除法：除以一個數字 \(x\) 代表「乘上 \(1/x\)」，也就是「和 \(x\) 乘會變成 \(1\) 的數字」，記作 \(x^{-1}\)
Ex. 模 \(10\) 底下，\(3^{-1} = 7\)、\(9^{-1} = 9\)、\(2\) 沒有模擬元
模 \(11\) 底下 \(3\) 的模擬元是多少？

找模擬元的方法

一個一個找：\(O(N)\), bad

時間是金啊啊啊啊啊！

~~如果AC了就可以拿獎金~~

找模擬元的方法

一個一個找：\(O(N)\), bad
輾轉相除法
費馬小 / 歐拉定理
線性找法

找模擬元的方法

一個一個找：\(O(N)\), bad
> 輾轉相除法
費馬小 / 歐拉定理
線性找法

解線性方程

從定義來看：令 \(x^{-1} = y\) 為我們想要找的東東
\(x \cdot y \equiv 1 \pmod{N}\)
\(\implies x \cdot y - 1 = N \cdot q\)
\(\implies x \cdot y - N \cdot q = 1\)
給定 \(x, N\) ，我們要找到 \(y, q\) ！

輾轉相除法 / 貝祖定理

對於任何 \(a, b\)，存在 \(u, v\) 使得

\(au + bv = \gcd(a, b)\)

\(x \cdot y - N \cdot q = 1\)

輾轉相除法 / 貝祖定理

對於任何 \(a, b\)，存在 \(u, v\) 使得

\(au + bv = d= \gcd(a, b)\)

且 \(au + bv\) 湊不出任何更小的解
有解若且唯若 \(\gcd(x, N)= 1\) ！

\(x \cdot y - N \cdot q = 1\)

找 \(au + bv = d\) 的解

目標：給定 \(a, b\) ，\(f(a, b)\) 找出 \(u, v, d\)
起始：若 \(a = 0\) 或 \(b = 0\) ，則我們知道 \(\gcd(a, b)\) 是非零的那個
遞迴：跑 \(f(a, b \% a)\)，得到 \(u', v', d\)
- \(au' + \left(b - a \cdot \lfloor \frac{b}{a}\rfloor\right)v'= d\)
- \(a\left(u' - \lfloor \frac{b}{a}\rfloor v'\right) + bv' = d\)
回傳 \(u = \left(u' - \lfloor \frac{b}{a}\rfloor v'\right), v = v', d= d\)

\(x \cdot y - N \cdot q = 1\)

找 \(au + bv = d\) 的解

目標：給定 \(a, b\) ，\(f(a, b)\) 找出 \(u, v, d\)
起始：若 \(a = 0\) 或 \(b = 0\) ，則我們知道 \(\gcd(a, b)\) 是非零的那個
遞迴：跑 \(f(a, b \% a)\)，得到 \(u', v', d\)
回傳 \(u = \left(u' - \lfloor \frac{b}{a}\rfloor v'\right), v = v', d= d\)

\(x \cdot y - N \cdot q = 1\)

int extended_euclidean(int a, int b, int &u, int &v) {
  if(!a || !b) {
    u = v = 1;
    return a ? a : b;
  } 
  int U, V;
  int d = extended_euclidean(b % a, a, U, V);
  u = U - (b / a) * V;
  v = V;
  return d;
}

找 \(xy - Nq = d\) 的解

\(x = O(N)\) 所以找 \(xy - Nq = 1\) 的時間是 \(O(\log N)\)

int extended_euclidean(int a, int b, int &u, int &v);

int modular_inverse(int x, int N) {
  int y, q;
  int d = extended_euclidean(x, N, y, q);
  if(d != 1) return 0; // inverse does not exist
  return y;
}

找模擬元的方法

一個一個找：\(O(N)\), bad
輾轉相除法
>> 費馬小 / 歐拉定理
線性找法

歐拉 \(\phi\) 函數

歐拉

歐拉歐拉歐拉歐拉

歐拉 \(\phi\) 函數的定義為：
\(\phi(n) = \{\#x: 1 \le x \le n \land \gcd(n, x) = 1\}\) （ \(1\) 到 \(n\) 中與 \(n\) 互值的數字的數量）

歐拉 \(\phi\) 函數

歐拉

歐拉歐拉歐拉歐拉

\(p\) 為質數，\(n, k,a, b\) 為正整數：
\(\phi(p) = p - 1\)
\(\phi(p^k) = p^k - p^{k - 1}\)
\(\gcd(a, b) = 1 \implies \phi(a)\phi(b) = \phi(ab)\)
\(\phi(n) = n \cdot\prod_{p | n} \left(\frac{p - 1}{p}\right)\)

每 \(p\) 個數字就有一個是 \(p\) 的倍數

Left as exercise ;(

歐拉定理 / 費馬小定理

倘若\(\gcd(a, n)\) 互質，則有

\(a^{\phi(n)} \equiv 1 \pmod{n}\) （歐拉定理）
特別是，如果 \(p\) 是質數，則

\(a^{p } \equiv a \pmod{p}\) （費馬小）

also left as exercise

sorry ;(

\(p = 5: 4^{5} = 1024 \equiv 4 \pmod{5}\)

\(p = 7: 3^{7} = 3^7 = 2187 \equiv 3 \pmod{7}\)

費馬小定理 - pf

假設：\(p\)為質數，且\(0 < a < p\)。

則：\(1, 2a, 3a, \dots, (p - 1)a\) 為

\(1, 2, 3, \dots, p - 1\) 的重新排列

ex. \(a = 3, p = 5\), 則 \(3, 6, 9, 12 \pmod{5}\) 為 \(3, 1, 4, 2\)

兩邊乘起來：\((p - 1)!a^{p - 1} \equiv (p - 1)! \pmod{p}\)

\(\implies p | \left[(p-1)!\left(a^{p - 1} - 1\right)\right]\)

\(\implies a^{p - 1} \equiv 1 \pmod{p}\)

歐拉定理 / 費馬小定理

\(a^{p - 1} \equiv 1 \pmod{p}\)
\(a^{p - 2} \cdot a \equiv 1\pmod{p}\)
\(a\) 的模逆元就是 \(a^{p - 2}\)！
我有辦法快速算一個數字模 \(p\) 的次方嗎？

快速幂

計算 \(b^e\pmod{p}\)
維護 \(b, b^2, b^4, b^8, \dots, b^{\left(2^{\lceil \log_2 e\rceil}\right)} \pmod{p}\) 再拼起來！
次方從\(1\)開始，如果有的話就乘上去！\(O(\log e)\)

int modexp(int b, int e, int p) { //b^e (mod p)
  int r = 1;
  while(e) {
    if(e & 1) r = r * b % p;
    b = b * b % p;
    e >>= 1;
  }
  return r;
}

快速幂求模逆元

若 \(p\) 是質數：\(a^{-1} \equiv a^{p - 2} \pmod{p}\)
\(O(\log p)\)

int modexp(int b, int e, int p) { //b^e (mod p)
  int r = 1;
  while(e) {
    if(e & 1) r = r * b % p;
    b = b * b % p;
    e >>= 1;
  }
  return r;
}

int modular_inverse(int x, int p) {
  return modexp(x, p - 2, p);
}

CSES - Exponentiation II

給定\(a, b, c\)，求 \(a^{\left(b^c\right)} \pmod{10^9 + 7}\)
\(N \le 10^5\) 筆詢問
\(0 \le a, b, c \le 10^9\)

找模逆元的方法

一個一個找：\(O(N)\), bad
輾轉相除法
費馬小 / 歐拉定理
>> 線性找法

線性求模逆元

求一個數字 \(M\) 的所有模逆元需要 \(O(M)\)，但是之後查詢就是 \(O(1)\)，若\(M\)不大的話可以壓掉一個 \(\log\)
有點嗑藥
假設已經求🉐️ \(x\) 以下的所有模逆元，現在要求 \(x\) 的模逆元。
\(M - x\lfloor\frac{M}{x}\rfloor \equiv (M \% x) \pmod{M}\)
\(- x\lfloor\frac{M}{x}\rfloor \cdot \left[(M \% x)^{-1}\right] \equiv (M \% x) \cdot \left[(M \% x)^{-1}\right] \equiv 1\pmod{M}\)
所以 \(x^{-1} = -\lfloor\frac{M}{x}\rfloor \cdot \left[(M \% x)^{-1}\right]\) ！

bad word

CSES - Binomial Coefficients

給定\(n, k\)，求 \(\binom{n}{k} = \frac{n!}{k!(n - k)!} \pmod{10^9 + 7}\)
\(N \le 10^5\) 筆詢問
\(0 \le k \le n \le 10^6\)

質數與它們的產地

Prime Numbers

如何判斷質數？

\(O(N)\) ：直接硬檢查

\(N = 10^9\) 就爆了⋯⋯

如何判斷質數？

\(O(N)\) ：直接硬檢查
\(O(\sqrt{N})\)：若有一個因數\(a\)，則\(a, N / a\) 其中一個一定不大於 \(\sqrt{N}\)，所以檢查 \(1\)到\(\sqrt{N}\)就好

如果只有一兩個數字， \(N = 10^{12}\) OK

but! 如果想要回答 \(1\) 到\(N\)內有幾個質數就 \(O(N \sqrt{N})\)，\(N = 10^6\) 也掰掰了

篩篩篩 - 埃拉托斯特尼篩法

一開始，每個數字都有可能是質數
對於每個數字的倍數
剩下的數字就是質數了 :D
複雜度：\(N + \frac{N}{2} + \frac{N}{3} + \dots + \frac{N}{N - 1} + \frac{N}{N} = O(N \log N)\)

const int maxN = 1e6 + 10;
isPrime[maxN];
std::vector<int> primes;

void sieve() {
  fill(isPrime, isPrime + maxN, true);
  for(int i = 1; i < maxN; i++) {
    if(i == 1) continue;
    if(isPrime[i]) primes.push_back(i);
    for(int j = 2 * i; j < maxN; j += i) isPrime[j] = false;
  }
}

⋯⋯結果篩出兩條線

篩篩篩 - 埃拉托斯特尼篩法 · 改

一開始，每個數字都有可能是質數
枚舉每個數字質數的倍數
剩下的數字就是質數了 :D
複雜度：\(\sum_{p \text{ prime}} \frac{N}{p} = O(N \log \log N)\) 維基百科證明，請小心服用

const int maxN = 1e6 + 10;
bool isPrime[maxN];
std::vector<int> primes;

void sieve() {
  fill(isPrime, isPrime + maxN, true);
  for(int i = 2; i < maxN; i++) {
    if(isPrime[i]) {
      primes.push_back(i);
      for(int j = 2 * i; j < maxN; j += i) isPrime[j] = false;
    }
  }
}

篩篩篩 - 歐拉篩

一開始，每個數字都有可能是質數
對於每個數字，把他的每個質數倍數都標記為不是質數
- 直到那個質數是自己的因數為止！
剩下的數字就是質數了 :D
複雜度：\(O(N)\)

const int maxN = 1e6 + 10;
isPrime[maxN];
std::vector<int> primes;

void sieve() {
  fill(isPrime, isPrime + maxN, true);
  for(int i = 2; i < maxN; i++) {
    if(isPrime[i]) {
      primes.push_back(i);
    }
    for(int p : primes) {
      if(i * p >= maxN) break;
      isPrime[i * p] = false;
      if(!(i % p)) break;
    }
  }
}

每一個數字 \(n\) 一定有一個最小質因數 \(p^*\)。在 i = \(n/p^*\) 和 p = \(p^*\) 的時候會被篩掉

補充：維護\(\phi\)函式

const int maxN = 1e6 + 10;
bool isPrime[maxN];
std::vector<int> primes;
int phi[maxN];

void sieve() {
  phi[1] = 1;
  fill(isPrime, isPrime + maxN, true);
  for(int i = 2; i < maxN; i++) {
    if(isPrime[i]) {
      phi[i] = 1;
      primes.push_back(i);
    }
    for(int p : primes) {
      if(i * p >= maxN) break;
      isPrime[i * p] = false;
      phi[i * p] = phi[i] * phi[p];
      if(!(i % p)) {
        phi[i * p] = phi[i] * p;
        break;
      }
    }
  }
}

\(\phi\) 的乘法規則：

\(\gcd(a, b) = 1\implies \phi(ab) = \phi(a)\phi(b)\)
\(\gcd(a, p) = p \implies \phi(ap) = p\cdot\phi(a)\)

TIOJ 1668 - 分組編隊

有 \(Q\) 筆詢問，每次都詢問 \(l_i, r_i\)

問 \([l_i, r_i]\) 裡頭有幾個質數？

\(Q < 20\)
\(2 \le l_i \le r_i < 2^{31}\)
\(r_i - l_i \le 2\times10^5\)

休息一下

Chinese Remainder Theorem

is useless

中國餘式定理

Chinese Remainder Theorem

《孫子算經》

資訊培訓還是逃不過文言文的魔爪⋯⋯

「今有物不知其數，三三數之剩二，五五數之剩三，七七數之剩二，問物幾何？」

《孫子算經》

資訊培訓還是逃不過文言文的魔爪⋯⋯

「今有物不知其數，三三數之剩二，五五數之剩三，七七數之剩二，問物幾何？」

所求 \(x\)

\(x \equiv 2 \pmod{3}\)

\(x \equiv 3 \pmod{5}\)

\(x \equiv 2 \pmod{7}\)

想要解的問題

求最小的 \(x\) 使得滿足以下 \(N\) 個條件

\(x \equiv a_1 \pmod{m_1}\)

\(x \equiv a_2 \pmod{m_2}\)

\(\vdots\)

\(x \equiv a_{N - 1} \pmod{m_{N - 1}}\)

\(x \equiv a_N \pmod{m_N}\)

或回傳其無解

\(N = 2\)

問題太難就把問題變簡單！！！

求最小的 \(x\) 使得滿足以下 \(N = 2\) 個條件

\(x \equiv a_1 \pmod{m_1}\)

\(x \equiv a_2 \pmod{m_2}\)

\(N = 2\)

\(x \equiv a_1 \pmod{m_1}\)

\(x \equiv a_2 \pmod{m_2}\)

\(x = m_1q + a_1 = m_2r + a_2\)

\(m_1q - m_2r = (a2 -a_1)\)

\(N = 2\)

\(m_1q - m_2r = (a2 -a_1)\)

擴展歐幾里德！

未知

Q: 以上有解的條件為？

\(N = 2\) - 細節

\(m_1q - m_2r = (a2 -a_1)\)
令 \(d = \gcd(m_1, m_2)\)
則我們可以找到\(m_1q' - m_2r' = d\) 的解
我們要的 \(q = q' \cdot \frac{(a2 -a_1)}{d}\)
\(x = m_1 \cdot \left(q' \cdot \frac{(a2 -a_1)}{d}\right) + a_1\) 是一個解

還有其他解嗎？

\(d\not| (a2 - a_1)\)即無解

\(N = 2\) - 細節

\(x = m_1 \cdot \left(q' \cdot \frac{(a2 -a_1)}{d}\right) + a_1\) 是一個解

還有其他解嗎？

如果 \(x\) 是一個解，則\(x \pm k \cdot \textrm{lcm}(m_1, m_2)\) 也是一組解！

不論是模\(m_1\)或\(m_2\)都會被消掉

\(N > 2\)：full CRT

\(x \equiv a_1 \pmod{m_1}\)

\(x \equiv a_2 \pmod{m_2}\)

\(\vdots\)

\(x \equiv a_{N - 1} \pmod{m_{N - 1}}\)

\(x \equiv a_N \pmod{m_N}\)

\(x \equiv b_1 \pmod{\textrm{lcm}(m_1, m_2)}\)

\(\vdots\)

\(x \equiv a_{N - 1} \pmod{m_{N - 1}}\)

\(x \equiv a_N \pmod{m_N}\)

減少一個式子

不斷套用 \(N = 2\) 最後就可以得到通式了！

Full CRT closed form

如果不想要那麼麻煩的話，其實也可以用算的：
令 \(M = \textrm{lcm}(m_1, m_2, \dots, m_N)\)，則

\(x = \prod_{i = 1}^{N} \frac{M}{m_i} \cdot \left(\frac{M}{m_i}\right)^{-1}\pmod{m_i}\cdot a_i\)

小插曲

Misc. Topics

剛剛的東西好無聊⋯⋯

中國餘式定理其實很少用到？
各種估複雜度很好用的等式
將唬爛 \(\rightarrow \) 正確演算法的好東東
隱藏版最重要的章節？？？

小知識 No. 1 —— 數論分塊

國外叫做 Harmonic Lemma 的樣子？
\(\{\lfloor \frac{N}{1}\rfloor, \lfloor \frac{N}{2}\rfloor, \lfloor \frac{N}{3}\rfloor, \dots,\lfloor \frac{N}{N -1}\rfloor, \lfloor \frac{N}{N}\rfloor\}\)
總共只有 \(O(\sqrt{N})\) 種不同的值！
proof:
\(\{\lfloor \frac{N}{1}\rfloor, \lfloor \frac{N}{2}\rfloor, \lfloor \frac{N}{3}\rfloor, \dots,\lfloor \frac{N}{\sqrt{N}}\rfloor\}\) 有至多 \(\sqrt{N}\) 個數字
對於 \(K > \sqrt{N}\)，\(\lfloor\frac{N}{K}\rfloor < \sqrt{N}\)，所以剩下的最多也只有 \(\sqrt{N}\) 種數字

小知識 No. 1 —— 數論分塊

for(int i = 1; i <= N; i++) {
  //N / i is the same for i = i ~ N / (N / i)
  //i is the smallest integer k s.t. N/i = N/k
}

\(\lfloor\frac{N}{i}\rfloor \le \frac{N}{k} \implies k \le \lfloor\frac{N}{\lfloor\frac{N}{i}\rfloor}\rfloor\)
也就是說，在 \(i \le k \le \lfloor\frac{N}{\lfloor\frac{N}{i}\rfloor}\rfloor\) 這個區間內， \(\frac{N}{k}\) 的值都相同！

小知識 No. 1 —— 數論分塊

const int M = 1e9 + 7, inv2 = 5e8 + 4;

int ans = 0;
for(int i = 1; i <= N; i++) {
  //N / i is the same for i = i ~ N / (N / i)
  //i is the smallest integer k s.t. N/i = N/k
  int l = i, r = N / (N / i)
  ans += (((N / i) * (l + r) % M) * (r - l + 1) % M) * inv2 % M;
  i = r;
}

\(\lfloor\frac{N}{i}\rfloor \le \frac{N}{k} \implies k \le \lfloor\frac{N}{\lfloor\frac{N}{i}\rfloor}\rfloor\)
也就是說，在 \(i \le k \le \lfloor\frac{N}{\lfloor\frac{N}{i}\rfloor}\rfloor\) 這個區間內， \(\frac{N}{k}\) 的值都相同！

Ex. 計算 \(\sum_{i = 1}^{N} i \cdot \lfloor\frac{N}{i}\rfloor\)

小知識 No. 2 —— 數論的界

\(\sum_{k = 1}^{N} \frac{1}{k} = O(\log N)\)
\(\sum_{k = 1}^{N} \frac{1}{k^2} < \frac{\pi^2}{6} = O(1)\)
\(N\) 以下約有 \(\frac{N}{\log N}\) 個質數（質數定理）
在合理的範圍（\(N \le 10^{18}\)內）， \(N\) 以下最多的因數的數字有 \(N^{1/3}\) 個因數

（證明略）

\(N\) 以下所有數字的因數數量和為 \(O(N \log N)\)

小知識 No. 3 —— 鴿籠原理

如果有 \(5\) 個鴿子飛進去 \(4\) 個籠子，一定存在一個籠子有兩個鴿子！

真的不是廢話啦

拿襪子問題

太棒了凌晨三點了來穿襪子吧
妳有黑白兩種襪子
妳至少要從抽屜中拿出幾個襪子才可以保證妳有一對顏色相同的襪子可以穿呢？

真的不是廢話啦

拿襪子問題

太棒了凌晨三點了來穿襪子吧
妳有黑白兩種襪子
妳至少要從抽屜中拿出幾個襪子才可以保證妳有一對顏色相同的襪子可以穿呢？
ANS：3 —— 兩個顏色的話三個襪子一定有兩個是成對的！

一一零零問題

對於任何一個數字 \(N\)，請證明存在一個數字 \(X\)符合
\(X\) 為 \(N\) 的倍數
\(X\) 為超過一個 \(1\) 之後接著一堆 \(0\) （也可以沒有）
Ex. \(N = 37\) 則 \(X = 111\) 符合；\(N = 2\) 則 \(X = 110, 1110, 10\) 皆符合

CF 961D - Pair of Lines

給定平面上 \(N\) 個點\((x_i, y_i)\)，請問有沒有辦法畫兩條線使得每一個點都在其中一條線上呢？
\(1 \le N \le 10^5\)
\(|x_i|, |y_i| \le 10^9\)

小知識 No. 4 —— 三角形

給定 \(N\) 個數字\(a_i\)，和 \(Q\) 個詢問，\([l_i, r_i]\)，問\([l_i, r_i]\) 內是否存在三個數字可以作為一個三角形的三邊長？

趴兔 —— 組合

Combinatorics

高中惡夢回來了！

通常在考慮「數數」、「機率」的時候會遇到
相信各位（可能或即將）都和高中排列組合不陌生吧！

基本名詞定義

\(n!\) 為 \(n\) 階乘，定義為\(n! = 1 \times 2 \times 3 \times \dots \times n\)
\(\binom{n}{k} = \frac{n!}{k!(n - k)!}\) 為二項式係數
小性質們：
- 帕斯卡三角形：\(\binom{n}{k - 1} + \binom{n}{k} = \binom{n + 1}{k}\)
- \(\binom{n}{k} = \binom{n}{n - k}\)
- \(\sum_{k = 0}^{N} \binom{N}{k} = 2^N\)
- 有沒有排列組合的證明呢？

小暖身

\(N\) 個相異物體有幾種排列？
\(N\) 個相同物體有幾種排列？
\(N\) 個相異物體中選出 \(K\) 個然後排列有幾種排列？
\(x_1 + x_2 + x_3 + \dots + x_N = X\) 有幾個非負整數解？
\(x_1 + x_2 + x_3 + \dots + x_N = X\) 有幾個正整數解？
\(x_1 + x_2 + x_3 + \dots + x_N \le X\) 有幾個非負整數解？

中暖身

從 \((0 ,0)\) 走到 \((N, M)\) 只往上走和只往右走有幾種方法？
有幾個長度為 \(N\) 的序列 \(\left<a_i\right>\) 滿足
- \(a_1 \le a_2 \le \dots \le a_N = K\)？

FHC '17 R1 - Beach Umbrellas

有 \(N \le 2000\) 個雨傘，各有半徑 \(1 \le r_i \le 10^9\)。現在妳想要將雨傘放在編號為 \(1, 2, 3, \dots, M\) ，的沙灘椅上（\(1 \le M \le 10^9\)）。所有的沙灘椅都連成一條線，且相鄰的沙灘椅的都相距 \(1\)。
請問有幾種讓雨傘展開後不會蓋到彼此的方法？

感謝 IOIC 講義提供例題 :D

排容原理（PIE）

請問 \(1\)~\(1000\) 內有幾個數字是 \(2, 3,\) 或 \(5\) 的倍數？

\(2, 3, 5\)：\(500, 333, 200\)
但有其中兩個的，像是 \(6, 15, 30\) 都被數到了兩次！扣掉扣掉
但是這樣滿足三個都是它的因數的又被扣掉了！再加一次
\(\textrm{Ans} = \lfloor\frac{1000}{2}\rfloor + \lfloor\frac{1000}{3}\rfloor + \lfloor\frac{1000}{5}\rfloor - \lfloor\frac{1000}{2 \cdot 3}\rfloor - \lfloor\frac{1000}{2 \cdot 5}\rfloor- \lfloor\frac{1000}{3 \cdot 5}\rfloor + \lfloor\frac{1000}{2 \cdot 3 \cdot 5}\rfloor \)

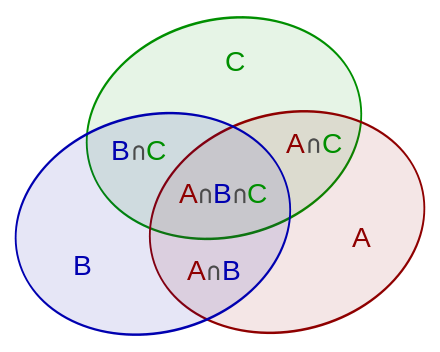
排容原理（PIE）| 數學定義

假設有 \(N\) 個集合 \(A = \{A_1, A_2, \dots, A_N\}\)。令 \([N] = \{1, 2, 3, \dots, N\}\)，且定義 \(A_J = \cap_{j \in J} A_j\)，\(A_{\emptyset} = \cup_{j \in [N]} A_j\)則：

\(\sum_{J \subseteq [N]} |A_J|\cdot(-1)^{|J|} = 0\)

\(N = 2\)：\(|A \cup B| - |A| - |B| - |A \cap B| = 0\)

排容原理（PIE）| 中文版

假設有 \(N\) 個集合 \(A = \{A_1, A_2, \dots, A_N\}\)。（通常每一個集合都滿足某個性質），然後妳想要算有幾個元素滿足所有的性質

先加上所有滿足至少一個性質的
再扣掉滿足至少兩個性質的
再加上滿足至少三個性質的
⋯⋯

TIOJ - 1086. 放錯的信封

妳是一個頑皮的郵差，有\(N\)封信，分別對應到\(N\)個家，第 \(i\) 封信就是要給第 \(i\) 個家的。頑皮的妳開始想了：有幾種放信的方法使得每戶人家都有拿到一封信，但是沒有人家拿到自己該拿到的信？請輸出答案 \(\pmod{10^9 + 7}\)。

\(N \le 1000\)

TIOJ - 1086. 放錯的信封

\(N \le 10^5\)

\(f(n) = \sum_{k = 0}^{N} \binom{n}{k} \cdot (n - k)! \cdot (-1)^k\)

選幾個家有被放到對的信，\(O(N \log N)\)

卡特蘭數列

卡特蘭數列（\(C_n\)）算的是：
- 長度為 \(2n\) 的合法括弧序列
- 在 \(n \times n\) 的方格上，從\((0, 0)\)走到\((n, n)\) 只走右上且不越過 \(y = x\) 這條線的走法
- 將凸 \(n + 2\) 邊形三角分割的方法數

()(())

((()))

()()()

(())()

卡特蘭數列

卡特蘭數列（\(C_n\)）算的是：
- \(C_1 = 1\)
- \(C_n = \sum_{k = 1}^{n - 1}C_kC_{n - k}\)（遞迴定義）
- \(C_n = \frac{1}{n + 1}\binom{2n}{n}\)（closed form）

()(())

((()))

()()()

(())()

遞迴方式解題

有時候，可以用類似 DP 的方式將一個題目分解成子題計算
Ex. 有 \(N\) 個相同的盒子，裡頭要分 \(M\) 個相異的物品的方法數：

枚舉有幾個非空箱子，令 \(S(n, k)\) 代表 \(n\) 個東西分在 \(k\) 個箱子裡頭，而且每一個箱子都有放至少一個東西。則
\(S(n, k) = S(n - 1, k - 1) + kS(n - 1, k)\)
(Stirling Numbers of the second kind)

約西弗斯問題

有 \(N\) 個人坐成一圈，順時針編號為 \(1, 2, \dots, N\)。\(1\) 號會往左邊數 \(K\) 個人，然後淘汰掉他，圈圈會變小。然後，坐在他左邊的人也會重複這件事情，一直到剩下一個人為止。請問這個人的編號為何？

約西弗斯問題

有 \(N\) 個人坐成一圈，順時針編號為 \(0, 2, \dots, N - 1\)。\(0\) 號會往左邊數 \(K\) 個人（包含自己），然後淘汰掉他，圈圈會變小。然後，坐在他左邊的人也會重複這件事情，一直到剩下一個人為止。請問這個人的編號為何？
令 \(f(N, K)\) 為所求的答案。則過了一輪之後從編號為 \(K\) 的人開始淘汰人，他所得到的答案為 \(f(N - 1, K)\)。則 \(f(N, K) = \left(f(N - 1, K) - K\right) \% N\)。

機率，期望值

Probability & Expected Values

機率和期望值

一個事件 \(E\) 的發生機率寫作 \(P(E)\)
一個隨機變數 \(X\) 並不是一個數字，而是具有隨機性的變數，它為 \(x\) 的機率為 \(P(X = x)\)。
一個隨機變數 \(X\) 的期望值定義為 \(\mathbb{E}[X] = \sum_{x = -\infty}^{\infty} x \cdot P(X = x)\)

可以理解為「觀察無限多次的話會得到的平均值」

經典題 - 簡單

一個硬幣有 \(p\) 的機率得到正面、\(1 - p\) 的機率得到反面 —— 連續丟 \(N\) 次硬幣得到的正面次數的期望值為何？

經典題 - 中等

數線上有 \(N = 500\) 個格子，編號由左至右為 \(1\) 到 \(N\)。現在，有一個機器人，他每一單位時間會隨機往左或往右，如果超出範圍就停止了。對於每一個 \(1 \le i \le N\)，請輸出如果這個機器人一開始在編號為 \(i\) 的格子的話，它要走到停的時間的期望值為何。

CF 839C - Journey

有一棵 \(N \le 10^5 \) 個節點的樹。有一隻馬一開始在節點 \(1\)，每一天都會隨機選條還沒走過的邊走，如果沒有的話他就會停；問牠要走的天數的期望值？

趴蘇里 —— 矩陣論

Matrix Theory

矩陣論聽起來好可怕

將線性代數中的矩陣拿出來特別討論
顧名思義就是在討論矩陣（？）
例子：\(A = \left(\begin{matrix} 1&2&3\\ 4&5&6\end{matrix}\right)\) 為 \(2\times 3\) 的矩陣
可以用來存很多的數字，是一種二維結構
C++ 通常就直接用二維陣列存了

矩陣的加法

矩陣可以做加法！兩個矩陣 \(A_{n\times m}, B_{n\times m}\) 的和就只是相對應的元素加起來：

\(\left(\begin{matrix} 1&2&3\\ 4&5&6\end{matrix}\right) + \left(\begin{matrix} 7&8&9\\ 5&8&1\end{matrix}\right) = \left(\begin{matrix} 8&10&12\\ 9&13&7\end{matrix}\right)\)

\(\left(A + B\right)_{ij} = A_{ij} + B_{ij}\)

矩陣的乘法

兩個矩陣 \(A_{n\times m}, B_{m\times k}\) 的乘法就比較複雜了，定義為：

\(\left(A\times B\right)_{ij} = \sum_{x = 1}^{m}A_{ix}B_{xj}\)

且其為一個 \(n \times k\)的矩陣。

\(\left(\begin{matrix} 1&2\\ 3 & 4\end{matrix}\right) \left(\begin{matrix} 4&-2\\-3&1\end{matrix}\right) = \left(\begin{matrix} -2&0\\ 0&-2\end{matrix}\right)\)

其中對角線為\(1\)，其餘元素為\(0\)的方陣寫作\(I_{n\times n}\)，為乘法單位元。

線性組合

如果想要解一個多元一次方程：
\(a_{11}x_1 + a_{12}x_2 + \dots + a_{1N} x_N = b_1\)
\(a_{21}x_1 + a_{22}x_2 + \dots + a_{2N} x_N = b_2\)
\(\vdots\)
\(a_{M1}x_1 + a_{M2}x_2 + \dots + a_{MN} x_N = b_M\)
則可以寫作
\(\left(\begin{matrix} a_{11}&a_{12}&\dots&a_{1N}\\ a_{21} & a_{22}&\dots&a_{2N}\\\vdots & \vdots&\ddots&\vdots\\ a_{M1}&a_{M2}&\dots&a_{MN}\\\end{matrix}\right) \left(\begin{matrix}x_1\\x_2\\\vdots\\x_N\end{matrix}\right) = \left(\begin{matrix}b_1\\b_2\\\vdots\\b_N\end{matrix}\right)\)

或
\(Ax = b\)

矩陣行運算

把矩陣的每一行想像成等式的話就很簡單啦！
\(R_i \rightarrow R_i + k\cdot R_j \) （兩式加起來）
\(R_i \rightarrow k \cdot R_i \)（乘常數）
\(R_i \leftrightarrow R_j \)（交換）

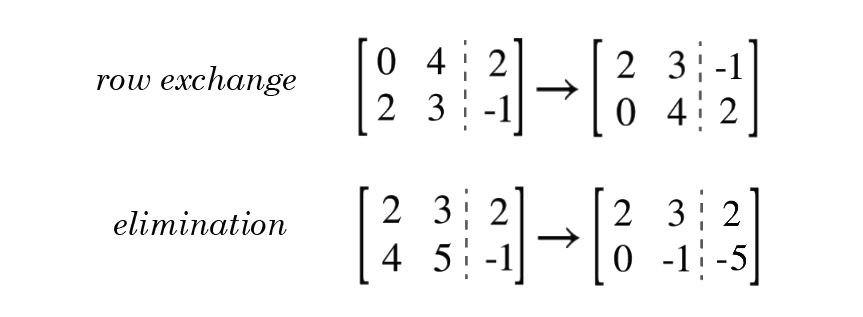
高斯消去法

對於第一（直）列，找到一個非零元素
把那一行交換上來
用這一行消去它以下的所有元素
重複！

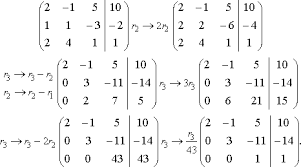
高斯消去法

對於第一（直）列，找到一個非零元素
把那一行交換上來
用這一行消去它以下的所有元素
重複！
之後再代入消去即可
好抽象⋯⋯

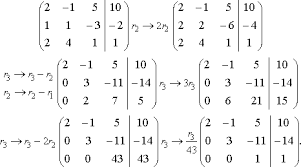
code dump

int GaussianElim(vector<vector<int>> A, vector<int> b, vector<int> &x) {
    //returns number of solutions: 0, 1, or 2 if infinite
    int N = A.size(), M = A[0].size();
    x = vector<int>(M);
    vector<int> where = vector<int>(M, -1);
    for(int row = 0, col = 0; col < M && row < N; col++) {
        int s = row;
        for(int i = row; i < N; i++) if(A[i][col]) s = i;
        if(!A[s][col]) continue;
        where[col] = row;
        for(int i = 0; i < M; i++) swap(A[s][i], A[row][i]);
        swap(b[s], b[row]);
        for(int i = 0; i < N; i++) if(i != row) {
           int f = A[i][col] * inv(A[row][col]) % MOD; 
           for(int j = 0; j < M; j++) {
               A[i][j] = sub(A[i][j], A[row][j] * f % MOD);
           }
           b[i] = sub(b[i], b[row] * f % MOD);
        }
        row++;
    }
    for(int i = 0; i < M; i++) if(where[i] != -1) {
        x[i] = b[where[i]] * inv(A[where[i]][i]) % MOD;
    }
}

線性遞迴

最經典的就是費波那契序列：

\(a_1 = a_2 = 1\)

\(a_k = a_{k - 1} + a_{k - 2}\)

要找到第\(N\) 項似乎需要 \(O(N)\) 時間

可以更快嗎？！

線性遞迴和矩陣的關係

其實遞迴關係式可以用矩陣表示！

\(\left(\begin{matrix}a_{n + 1} \\ a_n\end{matrix}\right)= \left(\begin{matrix}1 & 1 \\ 0&1\end{matrix}\right)\left(\begin{matrix}a_{n} \\ a_{n - 1}\end{matrix}\right)\)

\(\left(\begin{matrix}a_{n + 1} \\ a_n\end{matrix}\right)= \left(\begin{matrix}1 & 1 \\ 0&1\end{matrix}\right)^n\left(\begin{matrix}a_{1} \\ a_{0}\end{matrix}\right)\)

用快速幂就可以快速計算矩陣的幂次\(O(k^3 \log N)\) 通常比 \(O(N)\) 好超多 :D

Thank you!!

Q&A time

基礎數學

哈嘍各位！！！

https://rb.gy/zhpbpo

臺上的老人是誰？

正式課程前⋯⋯

今天會學到什麼

希望⋯⋯

趴萬 —— 數論

數論是什麼？

數字與它們的關係

Numbers and their relations

國小複習 + 名詞定義

最大公因數 / 最小公倍數

輾轉相除法

同餘

同餘的運算 明星三缺一

乘法模擬元

找模擬元的方法

時間是金啊啊啊啊啊！

找模擬元的方法

找模擬元的方法

解線性方程

輾轉相除法 / 貝祖定理

輾轉相除法 / 貝祖定理

找 \(au + bv = d\) 的解

找 \(au + bv = d\) 的解

找 \(xy - Nq = d\) 的解

找模擬元的方法

歐拉 \(\phi\) 函數

歐拉 \(\phi\) 函數

歐拉定理 / 費馬小定理

費馬小定理 - pf

歐拉定理 / 費馬小定理

快速幂

快速幂求模逆元

CSES - Exponentiation II

找模逆元的方法

線性求模逆元

CSES - Binomial Coefficients

質數與它們的產地

Prime Numbers

如何判斷質數？

如何判斷質數？

篩篩篩 - 埃拉托斯特尼篩法

篩篩篩 - 埃拉托斯特尼篩法 · 改

篩篩篩 - 歐拉篩

補充：維護\(\phi\)函式

TIOJ 1668 - 分組編隊

休息一下

Chinese Remainder Theorem

中國餘式定理

Chinese Remainder Theorem

《孫子算經》

《孫子算經》

想要解的問題

\(N = 2\)

\(N = 2\)

\(N = 2\)

\(N = 2\) - 細節

\(N = 2\) - 細節

\(N > 2\)：full CRT

Full CRT closed form

小插曲

Misc. Topics

剛剛的東西好無聊⋯⋯

小知識 No. 1 —— 數論分塊

小知識 No. 1 —— 數論分塊

小知識 No. 1 —— 數論分塊

小知識 No. 2 —— 數論的界

小知識 No. 3 —— 鴿籠原理

拿襪子問題

拿襪子問題

一一零零問題

CF 961D - Pair of Lines

小知識 No. 4 —— 三角形

趴兔 —— 組合

高中惡夢回來了！

基本名詞定義

小暖身

中暖身

同餘的運算明星三缺一