Metodologia Científica
Especialização em Análises Clínicas e Gestão Laboratorial
MSc. Laise de Moraes
Noções de Estatística e Epidemiologia

2019
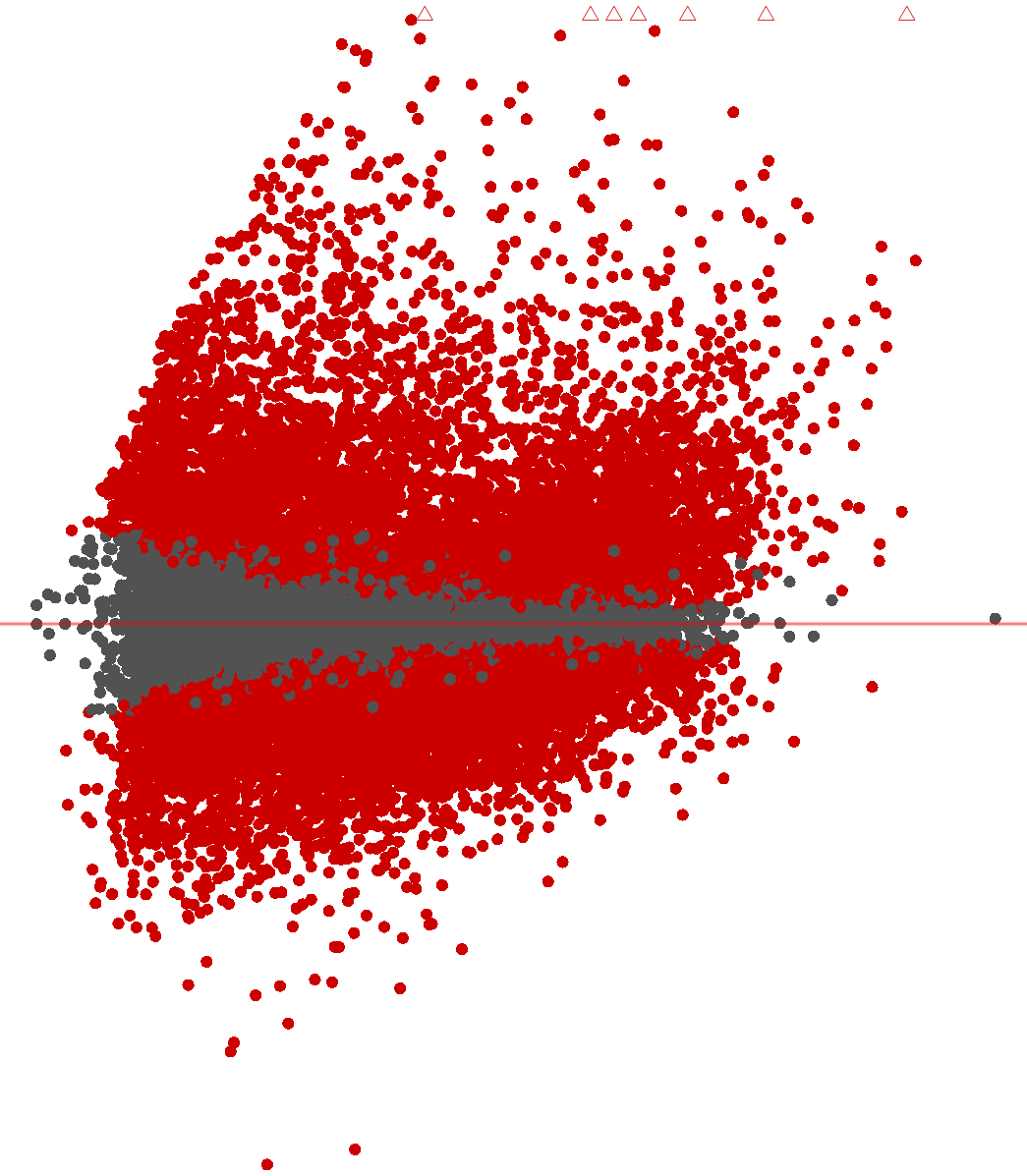
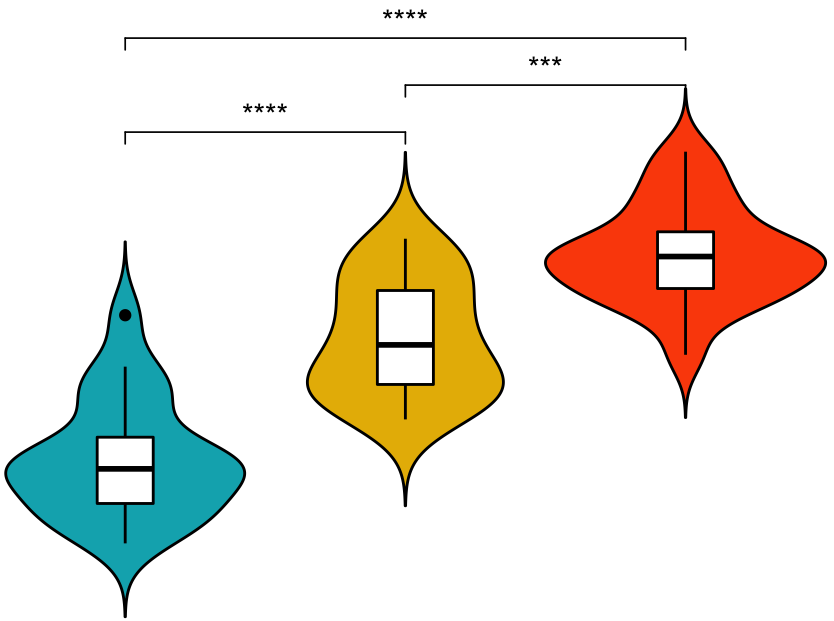
Por que precisamos entender estatística?
Por que precisamos entender estatística?
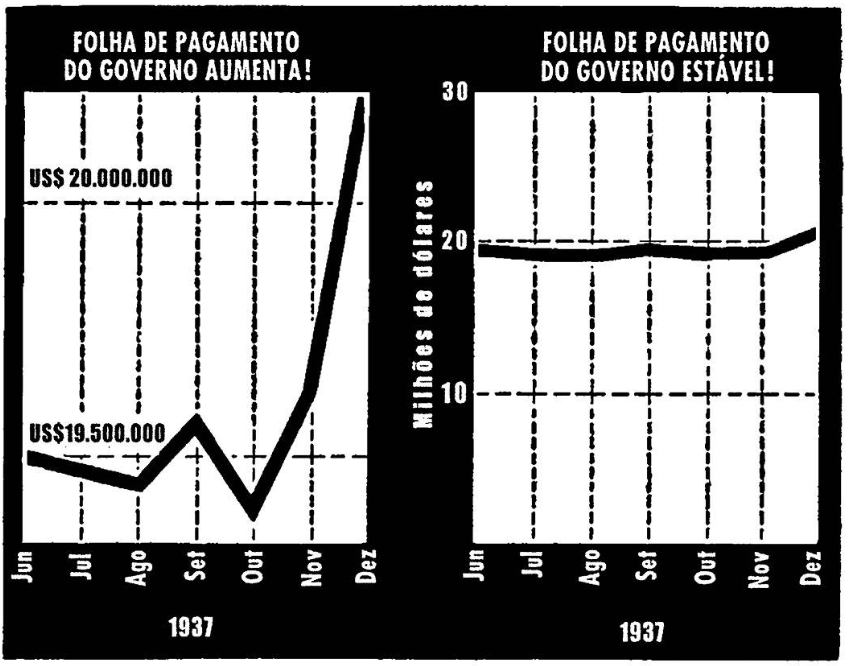
Por que precisamos entender estatística?

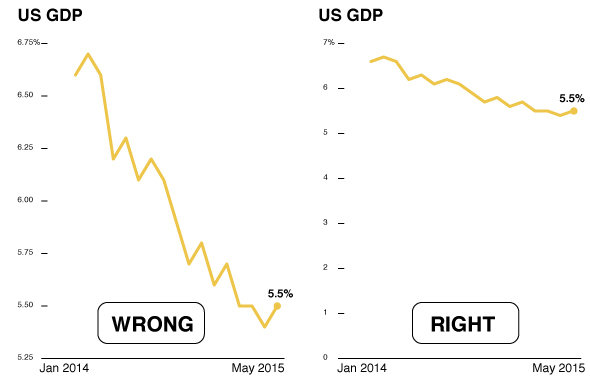
O PIB realmente teve mudanças exorbiantes?
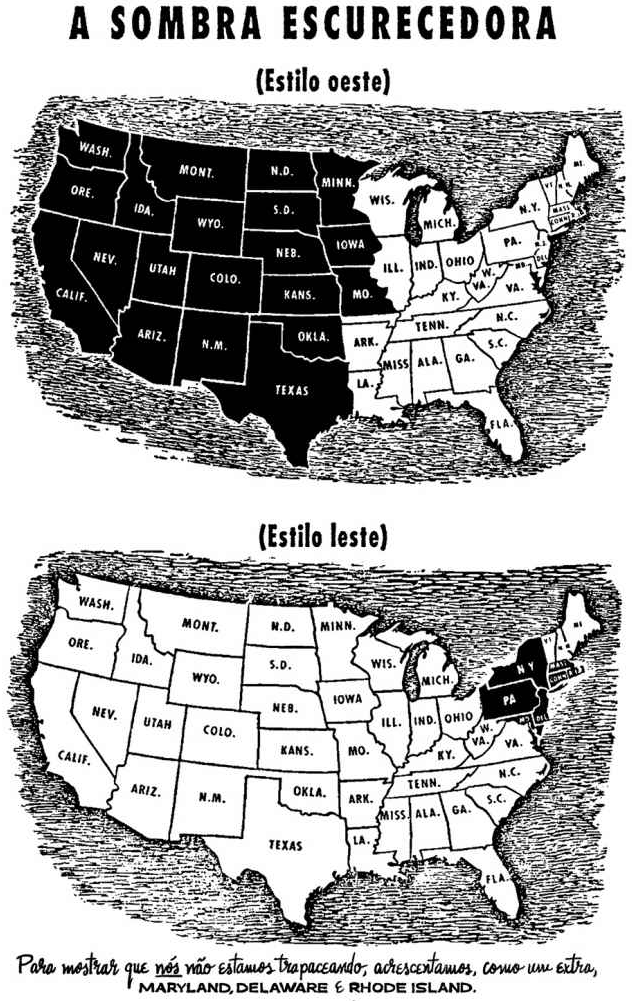
Por que precisamos entender estatística?

Por que precisamos entender estatística?

O que as cores te dizem?
Por que precisamos entender estatística?


Por que precisamos entender estatística?



12 crianças realmente são suficientes para generalizar esta informação?
Estatística DESCRITIVA vs INFERENCIAL
Estatística DESCRITIVA
-
Métodos estatísticos que visam resumir e descrever os dados
-
Apenas descrevem características das amostras
Estatística INFERENCIAL
-
Métodos estatísticos que viram inferir generalizações sobre uma população, utilizando uma amostra populacional
-
Compara grupos
Estudo científico no ponto de vista estatístico:
-
Definir a população de interesse
-
Selecionar uma amostra da população
-
Coletar dados
-
Utilizar estatística descritiva
-
Utilizar estatística analítica
-
Utilizar estatística inferencial
Silvany Neto AM. Bioestatística sem segredos. Salvador: Edição do autor; 2008. p. 27-8.
São características que variam entre os indivíduos estudados
NATUREZA
Qualitativa: sexo biológico, etnia
Quantitativa: peso, idade, altura, glicemia, carga viral
Discreta: número de filhos, número de infecções
Contínua: peso, idade, altura, glicemia, carga viral
CONTINUIDADE
CATEGORIA
Dicotômica: sexo biológico, hábito de fumar (sim/não)
Policotômica: religião, estado civil, time de futebol
ESCALA
Nominal: sexo biológico, CEP
Ordinal: escolaridade
Intervalar: temperatura
Quantitativa: peso, idade, altura
Variáveis
São características que variam entre os indivíduos estudados
NATUREZA
Qualitativa: sexo biológico, etnia
Quantitativa: peso, idade, altura, glicemia, carga viral
Discreta: número de filhos, número de infecções
Contínua: peso, idade, altura, glicemia, carga viral
CONTINUIDADE
CATEGORIA
Dicotômica: sexo biológico, hábito de fumar (sim/não)
Policotômica: religião, estado civil, time de futebol
ESCALA
Nominal: sexo biológico, CEP
Ordinal: escolaridade
Intervalar: temperatura
Quantitativa: peso, idade, altura
Variáveis
São características que variam entre os indivíduos estudados
NATUREZA
Qualitativa: sexo biológico, etnia
Quantitativa: peso, idade, altura, glicemia, carga viral
Discreta: número de filhos, número de infecções
Contínua: peso, idade, altura, glicemia, carga viral
CONTINUIDADE
CATEGORIA
Dicotômica: sexo biológico, hábito de fumar (sim/não)
Policotômica: religião, estado civil, time de futebol
ESCALA
Nominal: sexo biológico, CEP
Ordinal: escolaridade
Intervalar: temperatura
Quantitativa: peso, idade, altura
Variáveis
São características que variam entre os indivíduos estudados
NATUREZA
Qualitativa: sexo biológico, etnia
Quantitativa: peso, idade, altura, glicemia, carga viral
Discreta: número de filhos, número de infecções
Contínua: peso, idade, altura, glicemia, carga viral
CONTINUIDADE
CATEGORIA
Dicotômica: sexo biológico, hábito de fumar (sim/não)
Policotômica: religião, estado civil, time de futebol
ESCALA
Nominal: sexo biológico, CEP
Ordinal: escolaridade
Intervalar: temperatura
Quantitativa: peso, idade, altura
Variáveis
São características que variam entre os indivíduos estudados
NATUREZA
Qualitativa: sexo biológico, etnia
Quantitativa: peso, idade, altura, glicemia, carga viral
Discreta: número de filhos, número de infecções
Contínua: peso, idade, altura, glicemia, carga viral
CONTINUIDADE
CATEGORIA
Dicotômica: sexo biológico, hábito de fumar (sim/não)
Policotômica: religião, estado civil, time de futebol
ESCALA
Nominal: sexo biológico, CEP
Ordinal: escolaridade
Intervalar: temperatura
Quantitativa: peso, idade, altura
Variáveis
Variável independente principal
Variável independente secundária
Variável interveniente
pode causar influência indireta
As variáveis na construção da hipótese do estudo
depende da influência da variável independente
interesse do estudo
pode influenciar a associação principal
Variável dependente
Estatística
Descritiva
Como descrever os dados?
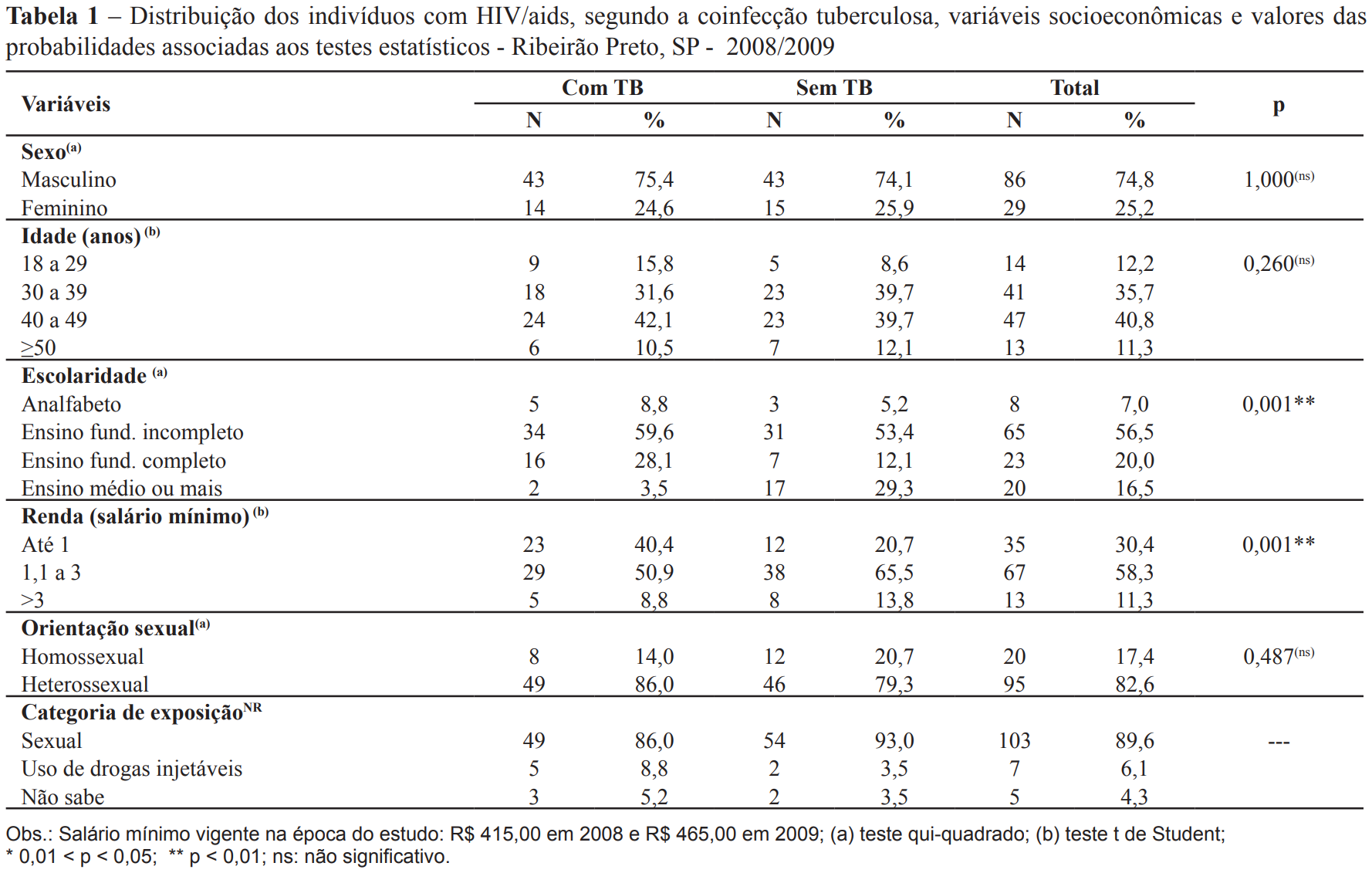
Neves Lis Aparecida de Souza, Canini Sílvia Rita Marin, Reis Renata Karina, Santos Cláudia Benedita dos, Gir Elucir. Aids e tuberculose: a coinfecção vista pela perspectiva da qualidade de vida dos indivíduos. Rev. esc. enferm. USP. 2012 June; 46(3):704-10. DOI: 10.1590/S0080-62342012000300024

Neves Lis Aparecida de Souza, Canini Sílvia Rita Marin, Reis Renata Karina, Santos Cláudia Benedita dos, Gir Elucir. Aids e tuberculose: a coinfecção vista pela perspectiva da qualidade de vida dos indivíduos. Rev. esc. enferm. USP. 2012 June; 46(3):704-10. DOI: 10.1590/S0080-62342012000300024
-
Tipos de dados estatísticos
-
Frequências
-
Medidas de tendência central
-
Medidas de posição
-
Medidas de dispersão
-
-
Apresentação de resultados
-
Tabela
-
Texto
-
Gráfico
-
Quadro
-
Como descrever os dados?

Neves Lis Aparecida de Souza, Canini Sílvia Rita Marin, Reis Renata Karina, Santos Cláudia Benedita dos, Gir Elucir. Aids e tuberculose: a coinfecção vista pela perspectiva da qualidade de vida dos indivíduos. Rev. esc. enferm. USP. 2012 June; 46(3):704-10. DOI: 10.1590/S0080-62342012000300024
-
Tipos de dados estatísticos
-
Frequências
-
Medidas de tendência central
-
Medidas de posição
-
Medidas de dispersão
-
No ano de 2008 e 2009, no município de Ribeirão Preto foram notificados 391 pacientes com TB sendo que 84 (21,5%) apresentavam sorologia positiva para o HIV. Foram entrevistados 57 pacientes coinfectados HIV/TB que atendiam aos critérios de inclusão e 58 indivíduos soropositivos para o HIV sem TB que estavam em acompanhamento ambulatorial, totalizando 115 participantes do estudo.
Do total de participantes, 86 (74,8%) eram do sexo masculino, com idade média de 40 anos, variando entre 18 e 62 anos; a faixa etária predominante foi dos 40 aos 49 anos (40,9%).
-
Apresentação de resultados
-
Tabela
-
Texto
-
Gráfico
-
Quadro
-
Como descrever os dados?
-
Tipos de dados estatísticos
-
Frequências
-
Medidas de tendência central
-
Medidas de posição
-
Medidas de dispersão
-
-
Apresentação de resultados
-
Tabela
-
Texto
-
Gráfico
-
Quadro
-
Como descrever os dados?
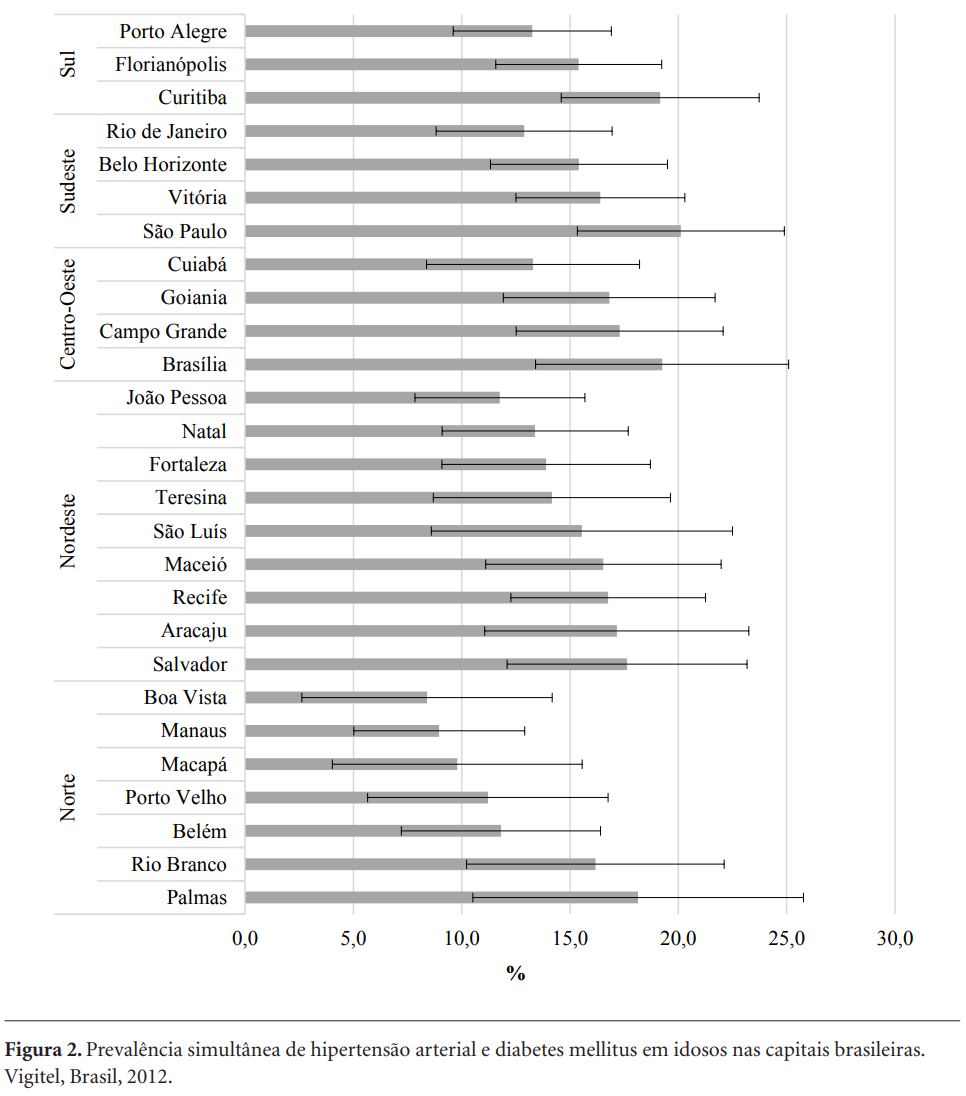
Francisco Priscila Maria Stolses Bergamo, Segri Neuber José, Borim Flávia Silva Arbex, Malta Deborah Carvalho. Prevalência simultânea de hipertensão e diabetes em idosos brasileiros: desigualdades individuais e contextuais. Ciênc. saúde coletiva. 2018 Nov;23(11):3829-3840. DOI: 10.1590/1413-812320182311.29662016.
Infecções Pulmonares na AIDS. Costa, CH. Brazilian Journal of Health and Biomedical Sciences. Vol.9, N.2 - Infecções Respiratórias. https://revista.hupe.uerj.br/detalhe_artigo.asp?id=161
-
Tipos de dados estatísticos
-
Frequências
-
Medidas de tendência central
-
Medidas de posição
-
Medidas de dispersão
-
-
Apresentação de resultados
-
Tabela
-
Texto
-
Gráfico
-
Quadro
-
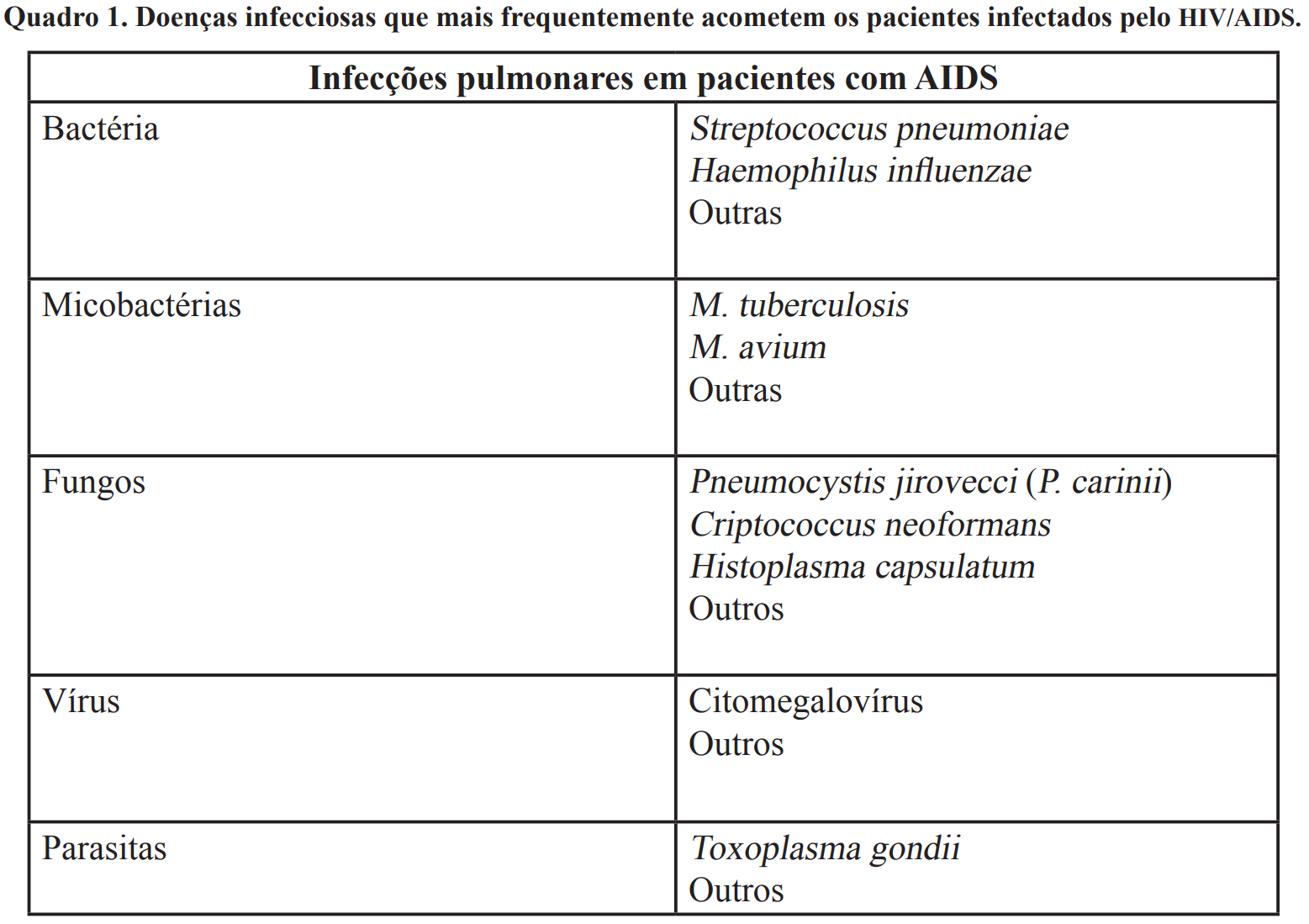
Como descrever os dados?
Como descrever os dados?
TIPOS DE DADOS ESTATÍSTICOS
CONTAGEM
- Exemplo: cor ou raça
-
Codificação para banco de dados:
- Amarela = 1
- Branca =2
- Indígena = 3
- Parda = 4
- Preta = 5
-
Recodificação:
- Branca = 1
- Não Branca = 2
MEDIÇÕES
- Glicemia, HDL, etc
- Transformação de medições em contagens:
- Categorização de variáveis contínuas
| Número do indivíduo da pesquisa | Idade |
|---|---|
| 1 | 36 |
| 2 | 45 |
| 3 | 40 |
| 4 | 23 |
| 5 | 23 |
| 6 | 16 |
| 7 | 79 |
| 8 | 56 |
| 9 | 56 |
| 10 | 43 |
| 11 | 40 |
| 12 | 21 |
| 13 | 23 |
| 14 | 19 |
| 15 | 90 |
- Tabela ou quadro?
- Qual indivíduo é o mais novo?
- Qual indivíduo é o mais velho?
- Quantos indivíduos tem 40 anos?
- Quantos indivíduos tem entre 20 e 50 anos?
Como descrever os dados?
- Tabela ou quadro?
- Qual indivíduo é o mais novo?
- Qual indivíduo é o mais velho?
- Quantos indivíduos tem 40 anos?
- Quantos indivíduos tem entre 20 e 50 anos?

Como descrever os dados?
| Número do indivíduo da pesquisa | Idade |
|---|---|
| 6 | 16 |
| 14 | 19 |
| 12 | 21 |
| 4 | 23 |
| 5 | 23 |
| 13 | 23 |
| 1 | 36 |
| 3 | 40 |
| 11 | 40 |
| 10 | 43 |
| 2 | 45 |
| 8 | 56 |
| 9 | 56 |
| 7 | 79 |
| 15 | 90 |

- Tabela ou quadro? QUADRO
- Qual indivíduo é o mais novo? 6
- Qual indivíduo é o mais velho? 15
- Quantos indivíduos tem 40 anos? 2
- Quantos indivíduos tem entre 20 e 50 anos? 9
Como descrever os dados?
| Número do indivíduo da pesquisa | Idade |
|---|---|
| 6 | 16 |
| 14 | 19 |
| 12 | 21 |
| 4 | 23 |
| 5 | 23 |
| 13 | 23 |
| 1 | 36 |
| 3 | 40 |
| 11 | 40 |
| 10 | 43 |
| 2 | 45 |
| 8 | 56 |
| 9 | 56 |
| 7 | 79 |
| 15 | 90 |
TIPOS DE FREQUÊNCIAS
| Idade | Frequência simples |
Frequência simples acumulada | Frequência relativa | Frequência relativa acumulada |
|---|---|---|---|---|
| 16 | 1 | 1 | 7% | 7% |
| 19 | 1 | 2 | 7% | 13% |
| 21 | 1 | 3 | 7% | 20% |
| 23 | 3 | 6 | 20% | 40% |
| 36 | 1 | 7 | 7% | 47% |
| 40 | 2 | 9 | 13% | 60% |
| 43 | 1 | 10 | 7% | 67% |
| 45 | 1 | 11 | 7% | 73% |
| 56 | 2 | 13 | 13% | 87% |
| 79 | 1 | 14 | 7% | 93% |
| 90 | 1 | 15 | 7% | 100% |
Como descrever os dados?
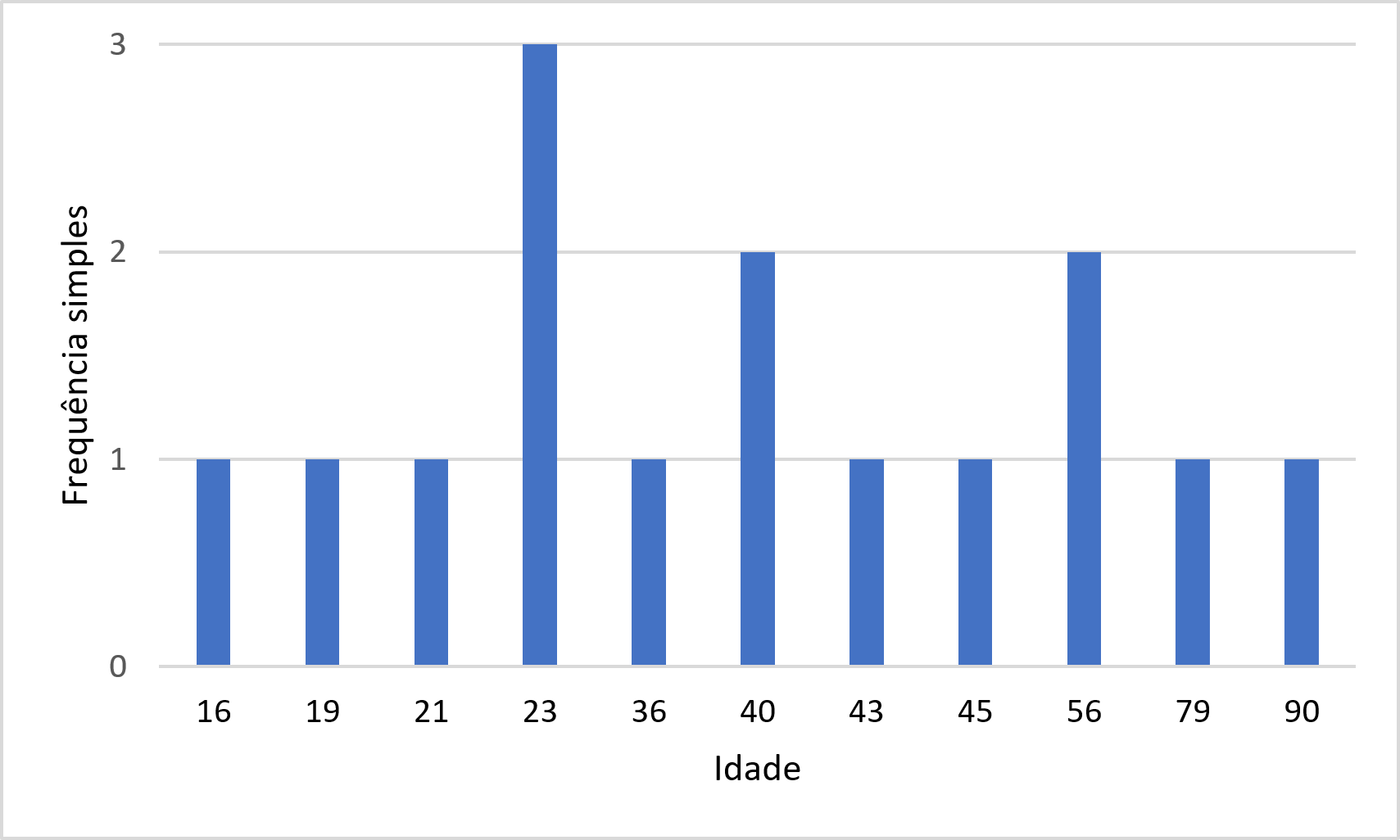
HISTOGRAMA CONTENDO A DISTRIBUIÇÃO DE FREQUÊNCIA DE IDADE
Como descrever os dados?
MEDIDAS DE TENDÊNCIA CENTRAL
- Moda: valor mais frequênte (bimodal, trimodal)
- Média: aritmética, ponderada
-
Mediana:
- n ímpar: posição central
- n par: média aritmética dos dois valores centrais
Como descrever os dados?
| Número do indivíduo da pesquisa | Idade |
|---|---|
| 6 | 16 |
| 14 | 19 |
| 12 | 21 |
| 4 | 23 |
| 5 | 23 |
| 13 | 23 |
| 1 | 36 |
| 3 | 40 |
| 11 | 40 |
| 10 | 43 |
| 2 | 45 |
| 8 | 56 |
| 9 | 56 |
| 7 | 79 |
| 15 | 90 |
- Moda: valor mais frequênte (bimodal, trimodal)
- Média: aritmética, ponderada
-
Mediana:
- n ímpar: posição central
- n par: média aritmética dos dois valores centrais
MEDIDAS DE TENDÊNCIA CENTRAL
moda = 23
média = 43
mediana = 40
Como descrever os dados?
| Número do indivíduo da pesquisa | Idade |
|---|---|
| 6 | 16 |
| 14 | 19 |
| 12 | 21 |
| 4 | 23 |
| 5 | 23 |
| 13 | 23 |
| 1 | 36 |
| 3 | 40 |
| 11 | 40 |
| 10 | 43 |
| 2 | 45 |
| 8 | 56 |
| 9 | 56 |
| 7 | 79 |
| 15 | 90 |
| VANTAGENS | DESVANTAGENS | |
|---|---|---|
| MODA | Não é afetada por valores extremos Pode resumir variável nominal |
Pode não ser única |
| MÉDIA | Singularidade Muitas técnicas disponíveis para seu uso |
Muito influenciada por valores extremos Não pode resumir variável nominal |
| MEDIANA | Singularidade Não é influenciada por valores extremos |
Menos técnicas disponÍveis para seu uso Não pode resumir variável nominal |
MEDIDAS DE TENDÊNCIA CENTRAL
Como descrever os dados?
Silvany Neto AM. Bioestatística sem segredos. Salvador: Edição do autor; 2008. p. 27-8.
Separa os valores de uma série de observações em partes ordenadas de forma crescente
Como descrever os dados?
MEDIDAS SEPARATRIZES
Q2 / mediana / porcentil 50
média
Q1 (porcentil 25)
porcentil 10
porcentil 90
Q3 (porcentil 75)
porcentil 100 / máximo /extremo
porcentil 1 / mínimo / extremo
oulier
oulier
IQR
25%
75%
2 PARTES: MEDIANA
4 PARTES: QUARTIL
10 PARTES: DECIL
100 PARTES: PORCENTIL
Silvany Neto AM. Bioestatística sem segredos. Salvador: Edição do autor; 2008. p. 27-8.
A informação fornecida pelas MEDIDAS DE POSIÇÃO CENTRAL sozinhas não trazem tanta informação:
Como descrever os dados?
| Altura |
|---|
| 1,45 |
| 1,62 |
| 1,42 |
| 1,80 |
| 1,55 |
| 1,81 |
| 1,82 |
| 1,83 |
| Altura |
|---|
| 1,44 |
| 1,72 |
| 1,40 |
| 1,79 |
| 1,48 |
| 1,83 |
| 1,70 |
| 1,94 |
| Altura |
|---|
| 1,34 |
| 1,82 |
| 1,30 |
| 1,89 |
| 1,38 |
| 1,93 |
| 1,60 |
| 2,04 |
GRUPO 2
GRUPO 1
GRUPO 3
A informação fornecida pelas MEDIDAS DE POSIÇÃO CENTRAL sozinhas não trazem tanta informação:
Como descrever os dados?
| Altura |
|---|
| 1,45 |
| 1,62 |
| 1,42 |
| 1,80 |
| 1,55 |
| 1,81 |
| 1,82 |
| 1,83 |
| Média = 1,66 |
| Mediana = 1,71 |
| Altura |
|---|
| 1,44 |
| 1,72 |
| 1,40 |
| 1,79 |
| 1,48 |
| 1,83 |
| 1,70 |
| 1,94 |
| Média = 1,66 |
| Mediana = 1,71 |
| Altura |
|---|
| 1,34 |
| 1,82 |
| 1,30 |
| 1,89 |
| 1,38 |
| 1,93 |
| 1,60 |
| 2,04 |
| Média = 1,66 |
| Mediana = 1,71 |
GRUPO 2
GRUPO 1
GRUPO 3
Como descrever os dados?
MEDIDAS DE DISPERSÃO
Indicam o quanto os dados são dispersos (variação) em todo da sua posição central.
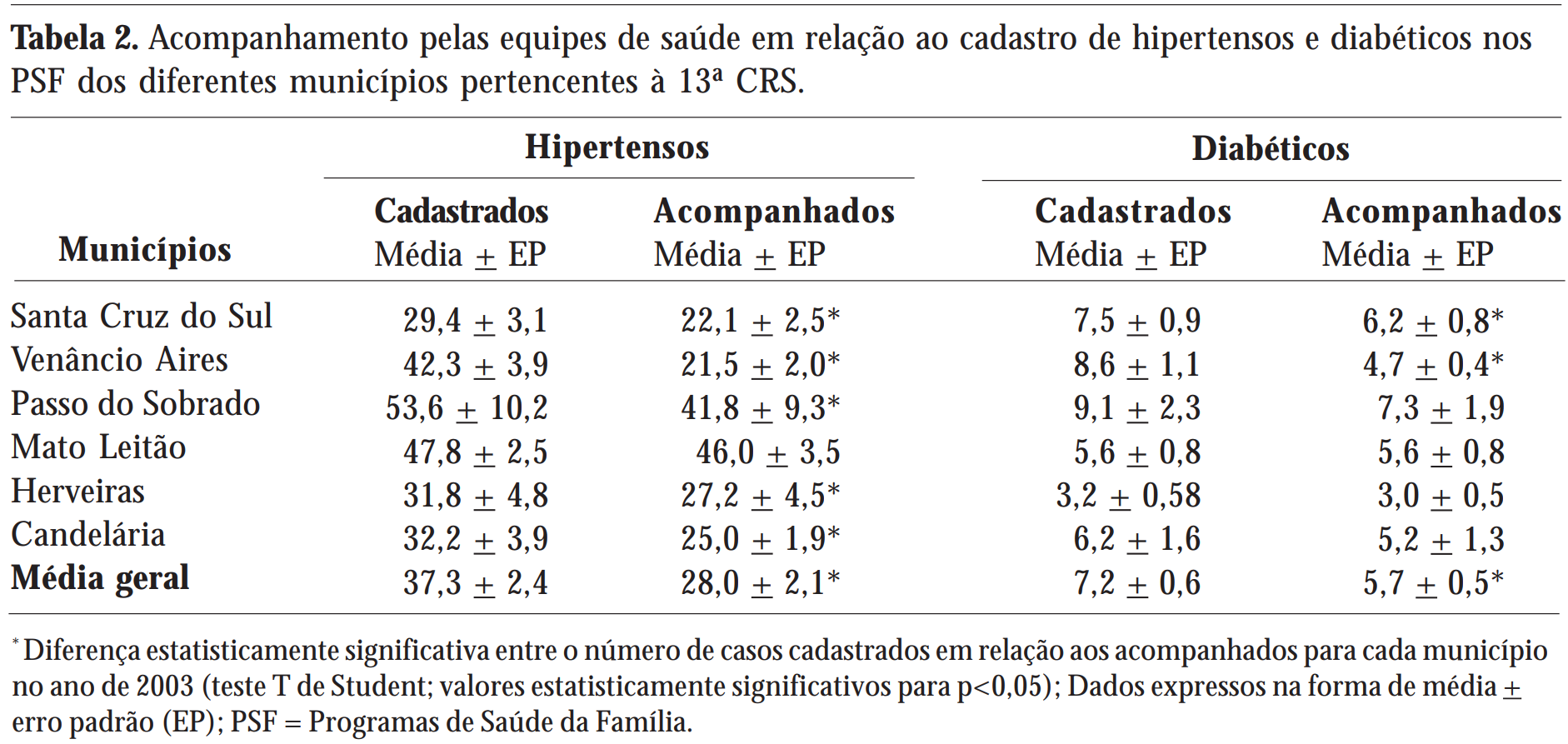
Malfatti Carlos Ricardo Maneck, Assunção Ari Nunes. Hipertensão arterial e diabetes na Estratégia de Saúde da Família: uma análise da frequência de acompanhamento pelas equipes de Saúde da Família. Ciênc. saúde coletiva. 2011;16(Suppl1):1383-1388. DOIS: 10.1590/S1413-81232011000700073.
Como descrever os dados?
MEDIDAS DE DISPERSÃO
Indicam o quanto os dados são dispersos (variação) em todo da sua posição central.
Amplitude é diferença entre o maior e o menor valor do conjunto de dados
GRUPO 2
GRUPO 1
GRUPO 3
| Altura |
|---|
| 1,45 |
| 1,62 |
| 1,42 |
| 1,80 |
| 1,55 |
| 1,81 |
| 1,82 |
| 1,83 |
| Média = 1,66 |
| Altura |
|---|
| 1,44 |
| 1,72 |
| 1,40 |
| 1,79 |
| 1,48 |
| 1,83 |
| 1,70 |
| 1,94 |
| Média = 1,66 |
| Altura |
|---|
| 1,34 |
| 1,82 |
| 1,30 |
| 1,89 |
| 1,38 |
| 1,93 |
| 1,60 |
| 2,04 |
| Média = 1,66 |
Silvany Neto AM. Bioestatística sem segredos. Salvador: Edição do autor; 2008. p. 27-8.
Como descrever os dados?
MEDIDAS DE DISPERSÃO
Indicam o quanto os dados são dispersos (variação) em todo da sua posição central.
Amplitude é diferença entre o maior e o menor valor do conjunto de dados
GRUPO 1: 1,83-1,42=0,41
GRUPO 2: 1,94-1,40=0,54
GRUPO 3: 2,04-1,30=0,74
GRUPO 2
GRUPO 1
GRUPO 3
| Altura |
|---|
| 1,45 |
| 1,62 |
| 1,42 |
| 1,80 |
| 1,55 |
| 1,81 |
| 1,82 |
| 1,83 |
| Média = 1,66 |
| Altura |
|---|
| 1,44 |
| 1,72 |
| 1,40 |
| 1,79 |
| 1,48 |
| 1,83 |
| 1,70 |
| 1,94 |
| Média = 1,66 |
| Altura |
|---|
| 1,34 |
| 1,82 |
| 1,30 |
| 1,89 |
| 1,38 |
| 1,93 |
| 1,60 |
| 2,04 |
| Média = 1,66 |
Silvany Neto AM. Bioestatística sem segredos. Salvador: Edição do autor; 2008. p. 27-8.
Como descrever os dados?
MEDIDAS DE DISPERSÃO
Indicam o quanto os dados são dispersos (variação) em todo da sua posição central.
Amplitude é diferença entre o maior e o menor valor do conjunto de dados
| VANTAGENS | DESVANTAGENS |
|---|---|
| Simples calcular | Considera apenas os valores máximo e mínimo Influenciada por valores extremos Poucas técnicas estatísticas que a utilizam* |
GRUPO 1: 1,83-1,42=0,41
GRUPO 2: 1,94-1,40=0,54
GRUPO 3: 2,04-1,30=0,74
GRUPO 2
GRUPO 1
GRUPO 3
| Altura |
|---|
| 1,45 |
| 1,62 |
| 1,42 |
| 1,80 |
| 1,55 |
| 1,81 |
| 1,82 |
| 1,83 |
| Média = 1,66 |
| Altura |
|---|
| 1,44 |
| 1,72 |
| 1,40 |
| 1,79 |
| 1,48 |
| 1,83 |
| 1,70 |
| 1,94 |
| Média = 1,66 |
| Altura |
|---|
| 1,34 |
| 1,82 |
| 1,30 |
| 1,89 |
| 1,38 |
| 1,93 |
| 1,60 |
| 2,04 |
| Média = 1,66 |
Silvany Neto AM. Bioestatística sem segredos. Salvador: Edição do autor; 2008. p. 27-8.
Como descrever os dados?
MEDIDAS DE DISPERSÃO
Indicam o quanto os dados são dispersos (variação) em todo da sua posição central.
Desvio médio reflete o quanto a medição se distanciou do valor da posição central do grupo
GRUPO 2
GRUPO 1
GRUPO 3
| Altura |
|---|
| 1,45 |
| 1,62 |
| 1,42 |
| 1,80 |
| 1,55 |
| 1,81 |
| 1,82 |
| 1,83 |
| Média = 1,66 |
| Altura |
|---|
| 1,44 |
| 1,72 |
| 1,40 |
| 1,79 |
| 1,48 |
| 1,83 |
| 1,70 |
| 1,94 |
| Média = 1,66 |
| Altura |
|---|
| 1,34 |
| 1,82 |
| 1,30 |
| 1,89 |
| 1,38 |
| 1,93 |
| 1,60 |
| 2,04 |
| Média = 1,66 |
Silvany Neto AM. Bioestatística sem segredos. Salvador: Edição do autor; 2008. p. 27-8.
Como descrever os dados?
MEDIDAS DE DISPERSÃO
Indicam o quanto os dados são dispersos (variação) em todo da sua posição central.
Desvio médio reflete o quanto a medição se distanciou do valor da posição central do grupo
Como calcular:
- Calcular a média do grupo
- Calcular quanto cada medição desviou da média do grupo
- Somar o módulo dos desvios
- Dividir pelo número de valores do grupo
GRUPO 2
GRUPO 1
GRUPO 3
| Altura |
|---|
| 1,45 |
| 1,62 |
| 1,42 |
| 1,80 |
| 1,55 |
| 1,81 |
| 1,82 |
| 1,83 |
| Média = 1,66 |
| Altura |
|---|
| 1,44 |
| 1,72 |
| 1,40 |
| 1,79 |
| 1,48 |
| 1,83 |
| 1,70 |
| 1,94 |
| Média = 1,66 |
| Altura |
|---|
| 1,34 |
| 1,82 |
| 1,30 |
| 1,89 |
| 1,38 |
| 1,93 |
| 1,60 |
| 2,04 |
| Média = 1,66 |
Silvany Neto AM. Bioestatística sem segredos. Salvador: Edição do autor; 2008. p. 27-8.
Como descrever os dados?
MEDIDAS DE DISPERSÃO
Indicam o quanto os dados são dispersos (variação) em todo da sua posição central.
Desvio médio reflete o quanto a medição se distanciou do valor da posição central do grupo
Como calcular:
- Calcular a média do grupo
- Calcular quanto cada medição desviou da média do grupo
- Somar o módulo dos desvios
- Dividir pelo total de valores do grupo
GRUPO 1: (|-0,21|+|-0,04|+|-0,24|+|0,14|+|-0,11|+|0,15|+|0,16|+|0,17|)/8=1,22/8≅0,15
GRUPO 2: (|-0,22|+|0,06|+|-0,26|+|0,13|+|-0,18|+|0,17|+|0,04|+|0,28|)/8=1,34/8≅1,09
GRUPO 3: (|-0,32|+|0,16|+|-0,36|+|0,23|+|-0,28|+|0,27|+|-0,06|+|0,38|)/8=2,06/8≅0,25
GRUPO 2
GRUPO 1
GRUPO 3
| Altura |
|---|
| 1,45 |
| 1,62 |
| 1,42 |
| 1,80 |
| 1,55 |
| 1,81 |
| 1,82 |
| 1,83 |
| Média = 1,66 |
| Altura |
|---|
| 1,44 |
| 1,72 |
| 1,40 |
| 1,79 |
| 1,48 |
| 1,83 |
| 1,70 |
| 1,94 |
| Média = 1,66 |
| Altura |
|---|
| 1,34 |
| 1,82 |
| 1,30 |
| 1,89 |
| 1,38 |
| 1,93 |
| 1,60 |
| 2,04 |
| Média = 1,66 |
Silvany Neto AM. Bioestatística sem segredos. Salvador: Edição do autor; 2008. p. 27-8.
Como descrever os dados?
MEDIDAS DE DISPERSÃO
Indicam o quanto os dados são dispersos (variação) em todo da sua posição central.
Desvio médio reflete o quanto a medição se distanciou do valor da posição central do grupo
Como calcular:
- Calcular a média do grupo
- Calcular quanto cada medição desviou da média do grupo
- Somar o módulo dos desvios
- Dividir pelo número de valores do grupo
GRUPO 1: (|-0,21|+|-0,04|+|-0,24|+|0,14|+|-0,11|+|0,15|+|0,16|+|0,17|)/8=1,22/8≅0,15
GRUPO 2: (|-0,22|+|0,06|+|-0,26|+|0,13|+|-0,18|+|0,17|+|0,04|+|0,28|)/8=1,34/8≅1,09
GRUPO 3: (|-0,32|+|0,16|+|-0,36|+|0,23|+|-0,28|+|0,27|+|-0,06|+|0,38|)/8=2,06/8≅0,25
| VANTAGENS | DESVANTAGENS |
|---|---|
| Leva em conta todos os valores da série Ao somar os módulos, expressa o total da variabilidade em torno da média |
Influenciado por valores extremos Menos técnicas estatísticas que o utilizam* |
GRUPO 2
GRUPO 1
GRUPO 3
| Altura |
|---|
| 1,45 |
| 1,62 |
| 1,42 |
| 1,80 |
| 1,55 |
| 1,81 |
| 1,82 |
| 1,83 |
| Média = 1,66 |
| Altura |
|---|
| 1,44 |
| 1,72 |
| 1,40 |
| 1,79 |
| 1,48 |
| 1,83 |
| 1,70 |
| 1,94 |
| Média = 1,66 |
| Altura |
|---|
| 1,34 |
| 1,82 |
| 1,30 |
| 1,89 |
| 1,38 |
| 1,93 |
| 1,60 |
| 2,04 |
| Média = 1,66 |
Silvany Neto AM. Bioestatística sem segredos. Salvador: Edição do autor; 2008. p. 27-8.
Como descrever os dados?
MEDIDAS DE DISPERSÃO
Indicam o quanto os dados são dispersos (variação) em todo da sua posição central.
Variância é a medida de dispersão que mostra o quão distante cada valor está da média
GRUPO 2
GRUPO 1
GRUPO 3
| Altura |
|---|
| 1,45 |
| 1,62 |
| 1,42 |
| 1,80 |
| 1,55 |
| 1,81 |
| 1,82 |
| 1,83 |
| Média = 1,66 |
| Altura |
|---|
| 1,44 |
| 1,72 |
| 1,40 |
| 1,79 |
| 1,48 |
| 1,83 |
| 1,70 |
| 1,94 |
| Média = 1,66 |
| Altura |
|---|
| 1,34 |
| 1,82 |
| 1,30 |
| 1,89 |
| 1,38 |
| 1,93 |
| 1,60 |
| 2,04 |
| Média = 1,66 |
Silvany Neto AM. Bioestatística sem segredos. Salvador: Edição do autor; 2008. p. 27-8.
Como descrever os dados?
MEDIDAS DE DISPERSÃO
Indicam o quanto os dados são dispersos (variação) em todo da sua posição central.
Como calcular:
- Calcular a média do grupo
- Calcular o quadrado do quanto cada medição desviou da média do grupo
- Somar os resultados da raiz quadrada
- Dividir pelo total de valores do grupo menos 1*
Variância é a medida de dispersão que mostra o quão distante cada valor está da média
Grau de liberdade
n-r
n = número de observações
r = número de condições a serem atendidas
GRUPO 2
GRUPO 1
GRUPO 3
| Altura |
|---|
| 1,45 |
| 1,62 |
| 1,42 |
| 1,80 |
| 1,55 |
| 1,81 |
| 1,82 |
| 1,83 |
| Média = 1,66 |
| Altura |
|---|
| 1,44 |
| 1,72 |
| 1,40 |
| 1,79 |
| 1,48 |
| 1,83 |
| 1,70 |
| 1,94 |
| Média = 1,66 |
| Altura |
|---|
| 1,34 |
| 1,82 |
| 1,30 |
| 1,89 |
| 1,38 |
| 1,93 |
| 1,60 |
| 2,04 |
| Média = 1,66 |
Silvany Neto AM. Bioestatística sem segredos. Salvador: Edição do autor; 2008. p. 27-8.
Como descrever os dados?
MEDIDAS DE DISPERSÃO
Indicam o quanto os dados são dispersos (variação) em todo da sua posição central.
Como calcular:
- Calcular a média do grupo
- Calcular o quadrado do quanto cada medição desviou da média do grupo
- Somar os resultados da raiz quadrada
- Dividir pelo total de valores do grupo menos 1
Variância é a medida de dispersão que mostra o quão distante cada valor está da média
GRUPO 1: [(-0,21)²+(-0,04)²+(-0,24)²+(0,14)²+(-0,11)²+(0,15)²+(0,16)²+(0,17)²]/8-1=0,21/7≅0,03
GRUPO 2: [(-0,22)²+(0,06)²+(-0,26)²+(0,13)²+(-0,18)²+(0,17)²+(0,04)²+(0,28²)]/8-1=0,28/7≅0,04
GRUPO 3: [(-0,32)²+(0,16)²+(-0,36)²+(0,23)²+(-0,28)²+(0,27)²+(-0,06)²+(0,38)²]/8-1=0,61/7≅0,09
Grau de liberdade
n-r
n = número de observações
r = número de condições a serem atendidas
GRUPO 2
GRUPO 1
GRUPO 3
| Altura |
|---|
| 1,45 |
| 1,62 |
| 1,42 |
| 1,80 |
| 1,55 |
| 1,81 |
| 1,82 |
| 1,83 |
| Média = 1,66 |
| Altura |
|---|
| 1,44 |
| 1,72 |
| 1,40 |
| 1,79 |
| 1,48 |
| 1,83 |
| 1,70 |
| 1,94 |
| Média = 1,66 |
| Altura |
|---|
| 1,34 |
| 1,82 |
| 1,30 |
| 1,89 |
| 1,38 |
| 1,93 |
| 1,60 |
| 2,04 |
| Média = 1,66 |
Silvany Neto AM. Bioestatística sem segredos. Salvador: Edição do autor; 2008. p. 27-8.
Como descrever os dados?
MEDIDAS DE DISPERSÃO
Indicam o quanto os dados são dispersos (variação) em todo da sua posição central.
Desvio padrão é a raiz quadrada positiva da variância
GRUPO 2
GRUPO 1
GRUPO 3
| Altura |
|---|
| 1,45 |
| 1,62 |
| 1,42 |
| 1,80 |
| 1,55 |
| 1,81 |
| 1,82 |
| 1,83 |
| Média = 1,66 |
| Altura |
|---|
| 1,44 |
| 1,72 |
| 1,40 |
| 1,79 |
| 1,48 |
| 1,83 |
| 1,70 |
| 1,94 |
| Média = 1,66 |
| Altura |
|---|
| 1,34 |
| 1,82 |
| 1,30 |
| 1,89 |
| 1,38 |
| 1,93 |
| 1,60 |
| 2,04 |
| Média = 1,66 |
Silvany Neto AM. Bioestatística sem segredos. Salvador: Edição do autor; 2008. p. 27-8.
Como descrever os dados?
MEDIDAS DE DISPERSÃO
Indicam o quanto os dados são dispersos (variação) em todo da sua posição central.
Desvio padrão é a raiz quadrada positiva da variância
Como calcular:
- Calcular a média do grupo
- Calcular a variância
- Realizar a raiz quadrada da variância
É o mesmo que dizer que a variância é o desvio padrão ao quadrado
GRUPO 2
GRUPO 1
GRUPO 3
| Altura |
|---|
| 1,45 |
| 1,62 |
| 1,42 |
| 1,80 |
| 1,55 |
| 1,81 |
| 1,82 |
| 1,83 |
| Média = 1,66 |
| Altura |
|---|
| 1,44 |
| 1,72 |
| 1,40 |
| 1,79 |
| 1,48 |
| 1,83 |
| 1,70 |
| 1,94 |
| Média = 1,66 |
| Altura |
|---|
| 1,34 |
| 1,82 |
| 1,30 |
| 1,89 |
| 1,38 |
| 1,93 |
| 1,60 |
| 2,04 |
| Média = 1,66 |
Silvany Neto AM. Bioestatística sem segredos. Salvador: Edição do autor; 2008. p. 27-8.
Como descrever os dados?
MEDIDAS DE DISPERSÃO
Indicam o quanto os dados são dispersos (variação) em todo da sua posição central.
Desvio padrão é a raiz quadrada positiva da variância
Como calcular:
- Calcular a média do grupo
- Calcular a variância
- Realizar a raiz quadrada da variância
É o mesmo que dizer que a variância é o desvio padrão ao quadrado
GRUPO 1: √0,03=0,17
GRUPO 2: √0,04=0,20
GRUPO 3: √0,09=0,30
GRUPO 2
GRUPO 1
GRUPO 3
| Altura |
|---|
| 1,45 |
| 1,62 |
| 1,42 |
| 1,80 |
| 1,55 |
| 1,81 |
| 1,82 |
| 1,83 |
| Média = 1,66 |
| Altura |
|---|
| 1,44 |
| 1,72 |
| 1,40 |
| 1,79 |
| 1,48 |
| 1,83 |
| 1,70 |
| 1,94 |
| Média = 1,66 |
| Altura |
|---|
| 1,34 |
| 1,82 |
| 1,30 |
| 1,89 |
| 1,38 |
| 1,93 |
| 1,60 |
| 2,04 |
| Média = 1,66 |
Silvany Neto AM. Bioestatística sem segredos. Salvador: Edição do autor; 2008. p. 27-8.
Como descrever os dados?
MEDIDAS DE DISPERSÃO
Indicam o quanto os dados são dispersos (variação) em todo da sua posição central.
Desvio padrão é a raiz quadrada positiva da variância
Como calcular:
- Calcular a média do grupo
- Calcular a variância
- Realizar a raiz quadrada da variância
É o mesmo que dizer que a variância é o desvio padrão ao quadrado
GRUPO 1: √0,03=0,17
GRUPO 2: √0,04=0,20
GRUPO 3: √0,09=0,30
GRUPO 2
GRUPO 1
GRUPO 3
| Altura |
|---|
| 1,45 |
| 1,62 |
| 1,42 |
| 1,80 |
| 1,55 |
| 1,81 |
| 1,82 |
| 1,83 |
| Média = 1,66 |
| Altura |
|---|
| 1,44 |
| 1,72 |
| 1,40 |
| 1,79 |
| 1,48 |
| 1,83 |
| 1,70 |
| 1,94 |
| Média = 1,66 |
| Altura |
|---|
| 1,34 |
| 1,82 |
| 1,30 |
| 1,89 |
| 1,38 |
| 1,93 |
| 1,60 |
| 2,04 |
| Média = 1,66 |
Desvio padrão é chamado de Erro padrão quando aplicado para comparar grupos
Silvany Neto AM. Bioestatística sem segredos. Salvador: Edição do autor; 2008. p. 27-8.
MEDIDAS DE DISPERSÃO
Indicam o quanto os dados são dispersos (variação) em todo da sua posição central.
Desvio padrão
Como descrever os dados?
Variância
| VANTAGENS | DESVANTAGENS |
|---|---|
| Levam em conta todos os valores da medição Ao somar os quadrados dos desvios, expressam o total de variabilidade em torno da média Os desvios maiores influenciam bem mais seu resultado do que os menores Muitas técnicas estatísticas os utlizam |
Influenciados por valores extremos A variância é expressa em escala quadrática, á qual estamos menos acostumados |
Silvany Neto AM. Bioestatística sem segredos. Salvador: Edição do autor; 2008. p. 27-8.
Como visualizar os dados?
TABELAS
ATENÇÃO! QUADROS NÃO SÃO UTILIZADOS PARA APRESENTAR INFORMAÇÕES QUANTITATIVAS
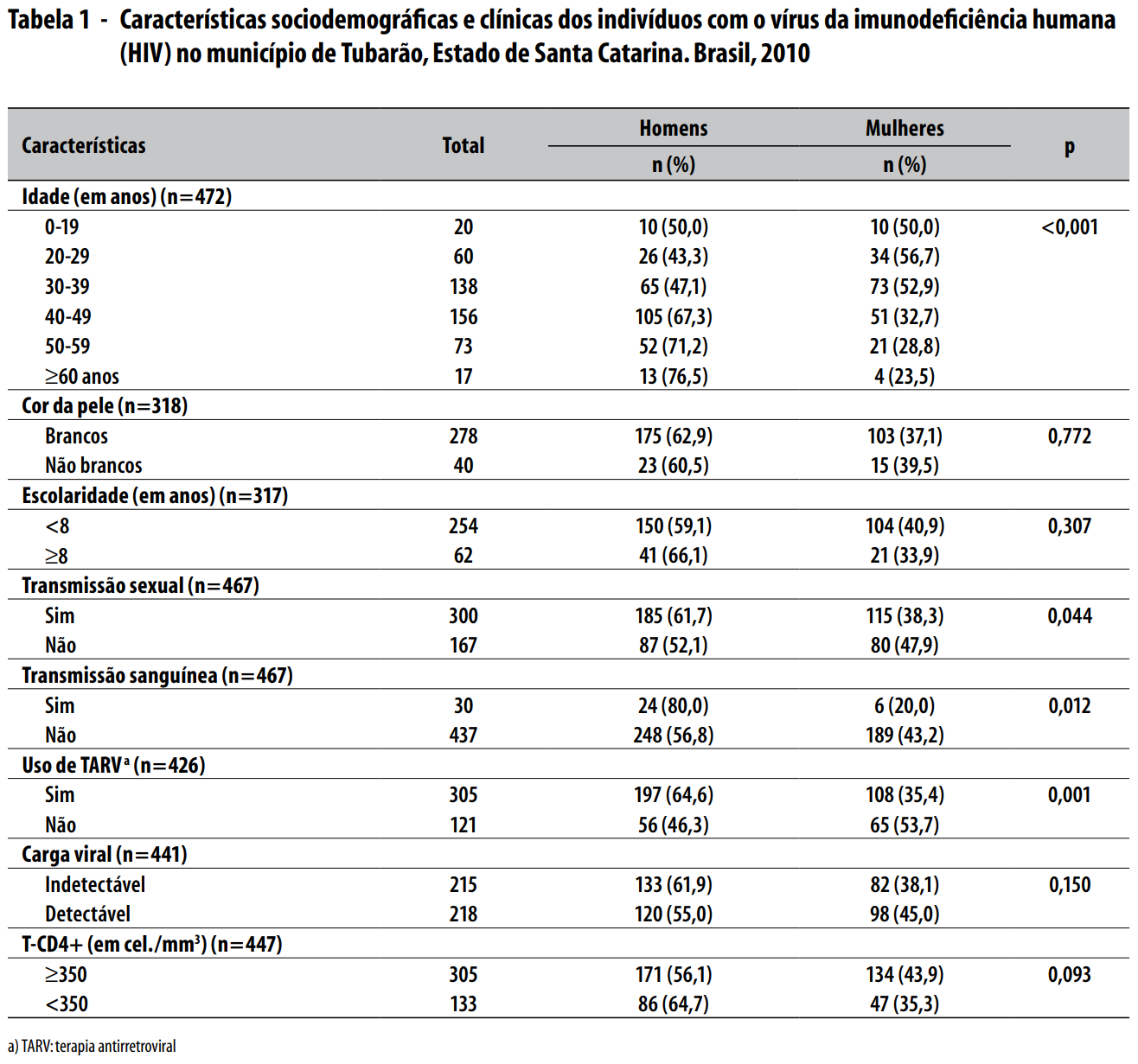
Schuelter-Trevisol Fabiana, Paolla Pucci, Justino Ariane Zanetta, Pucci Nicole, Silva Ana Carolina Barreto da. Perfil epidemiológico dos pacientes com HIV atendidos no sul do Estado de Santa Catarina, Brasil, em 2010. Epidemiol. Serv. Saúde. 2013 Mar;22(1):87-94. DOI: 10.5123/S1679-49742013000100009.
Como visualizar os dados?
TABELAS
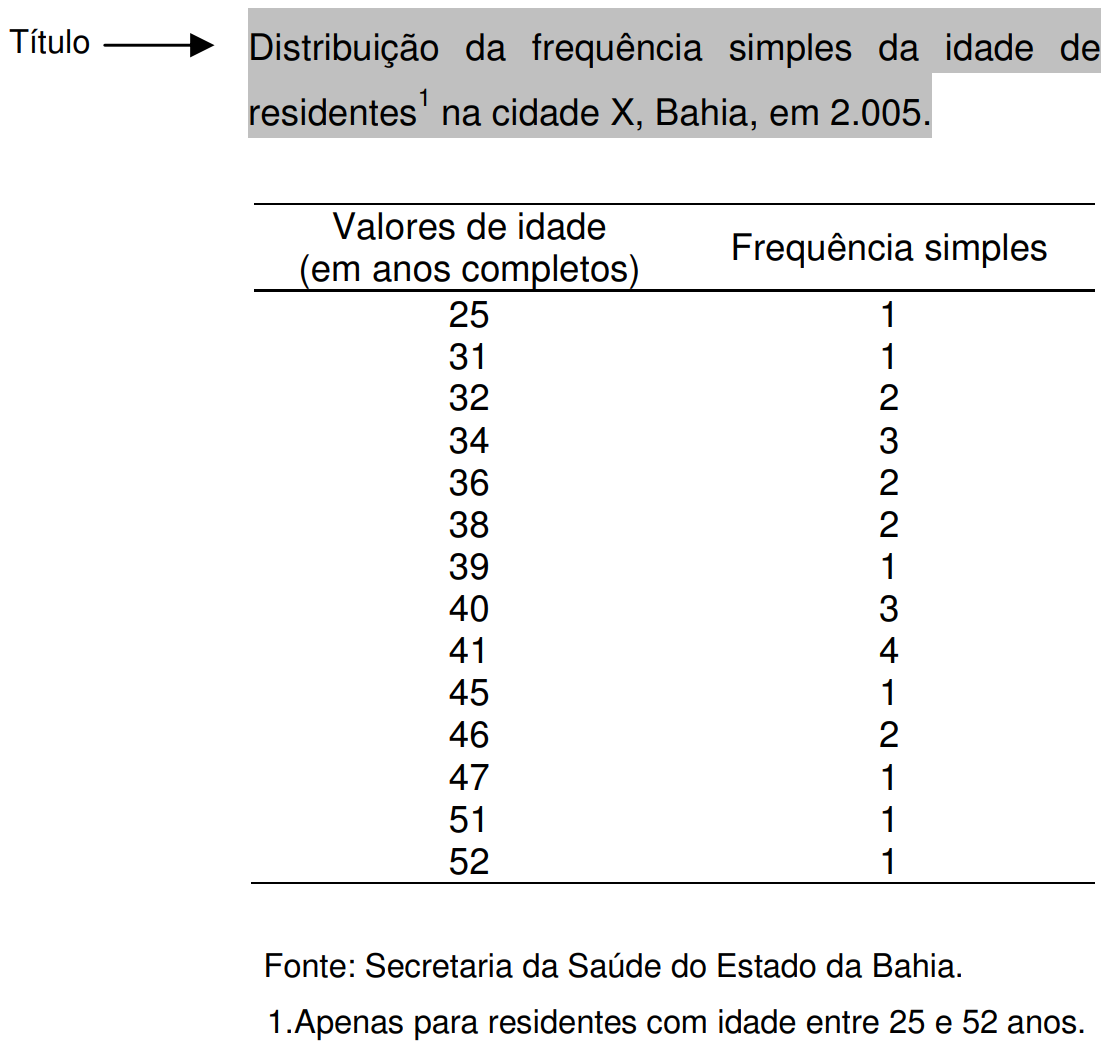

ATENÇÃO! QUADROS NÃO SÃO UTILIZADOS PARA APRESENTAR INFORMAÇÕES QUANTITATIVAS
Silvany Neto AM. Bioestatística sem segredos. Salvador: Edição do autor; 2008. p. 27-8.
Como visualizar os dados?
TABELAS


ATENÇÃO! QUADROS NÃO SÃO UTILIZADOS PARA APRESENTAR INFORMAÇÕES QUANTITATIVAS
Silvany Neto AM. Bioestatística sem segredos. Salvador: Edição do autor; 2008. p. 27-8.
Como visualizar os dados?
TABELAS


ATENÇÃO! QUADROS NÃO SÃO UTILIZADOS PARA APRESENTAR INFORMAÇÕES QUANTITATIVAS
Silvany Neto AM. Bioestatística sem segredos. Salvador: Edição do autor; 2008. p. 27-8.
Como visualizar os dados?
TABELAS

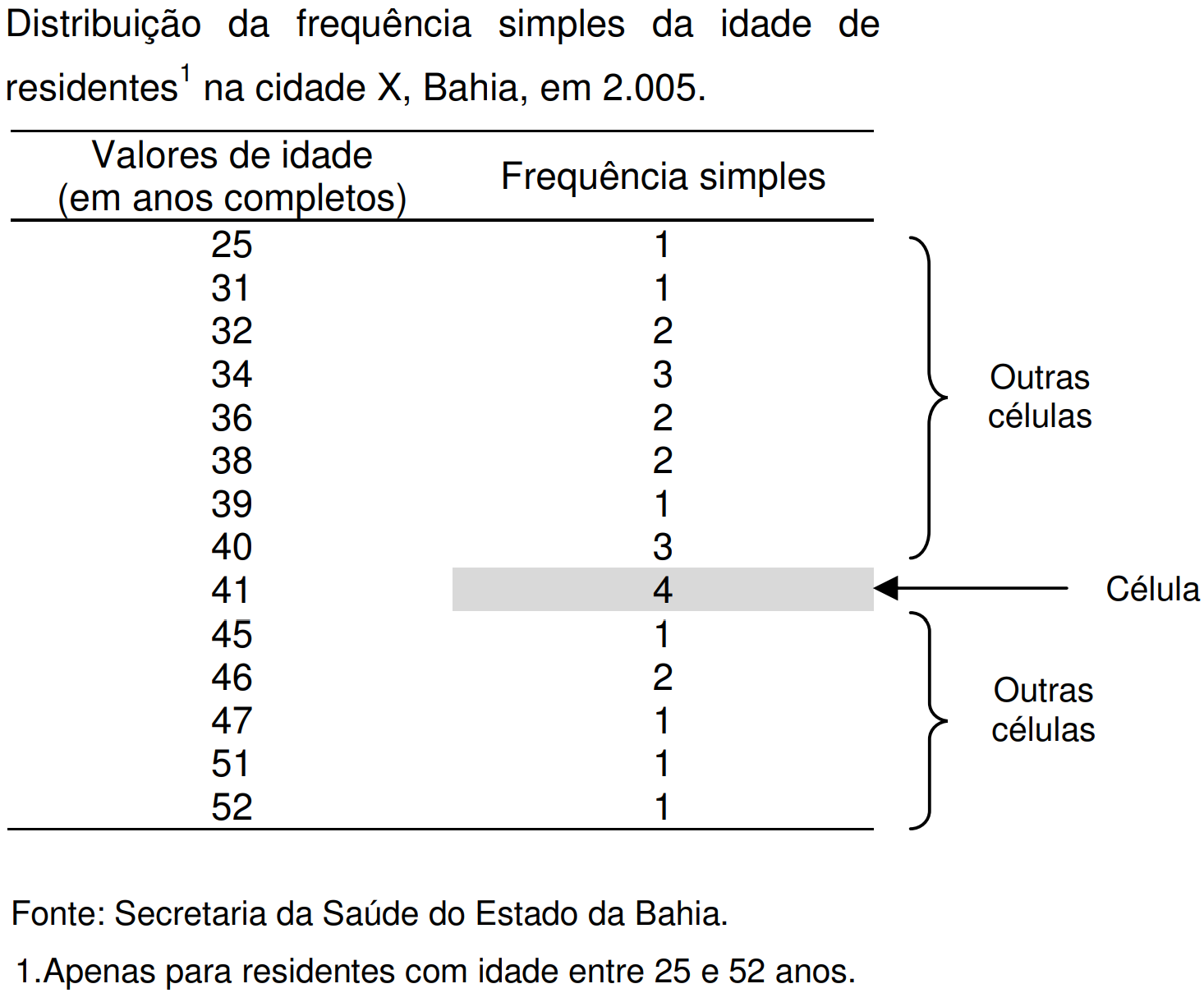
ATENÇÃO! QUADROS NÃO SÃO UTILIZADOS PARA APRESENTAR INFORMAÇÕES QUANTITATIVAS
Silvany Neto AM. Bioestatística sem segredos. Salvador: Edição do autor; 2008. p. 27-8.
Como visualizar os dados?
TABELAS


ATENÇÃO! QUADROS NÃO SÃO UTILIZADOS PARA APRESENTAR INFORMAÇÕES QUANTITATIVAS
Silvany Neto AM. Bioestatística sem segredos. Salvador: Edição do autor; 2008. p. 27-8.
Como visualizar os dados?
CARTOGRAMAS
Rothan, Hussin & R.M. Bidokhti, Mehdi & Siddappa, Nagadenahalli. (2018). Current concerns and perspectives on Zika virus co-infection with arboviruses and HIV. Journal of Autoimmunity. 89. 10.1016/j.jaut.2018.01.002.
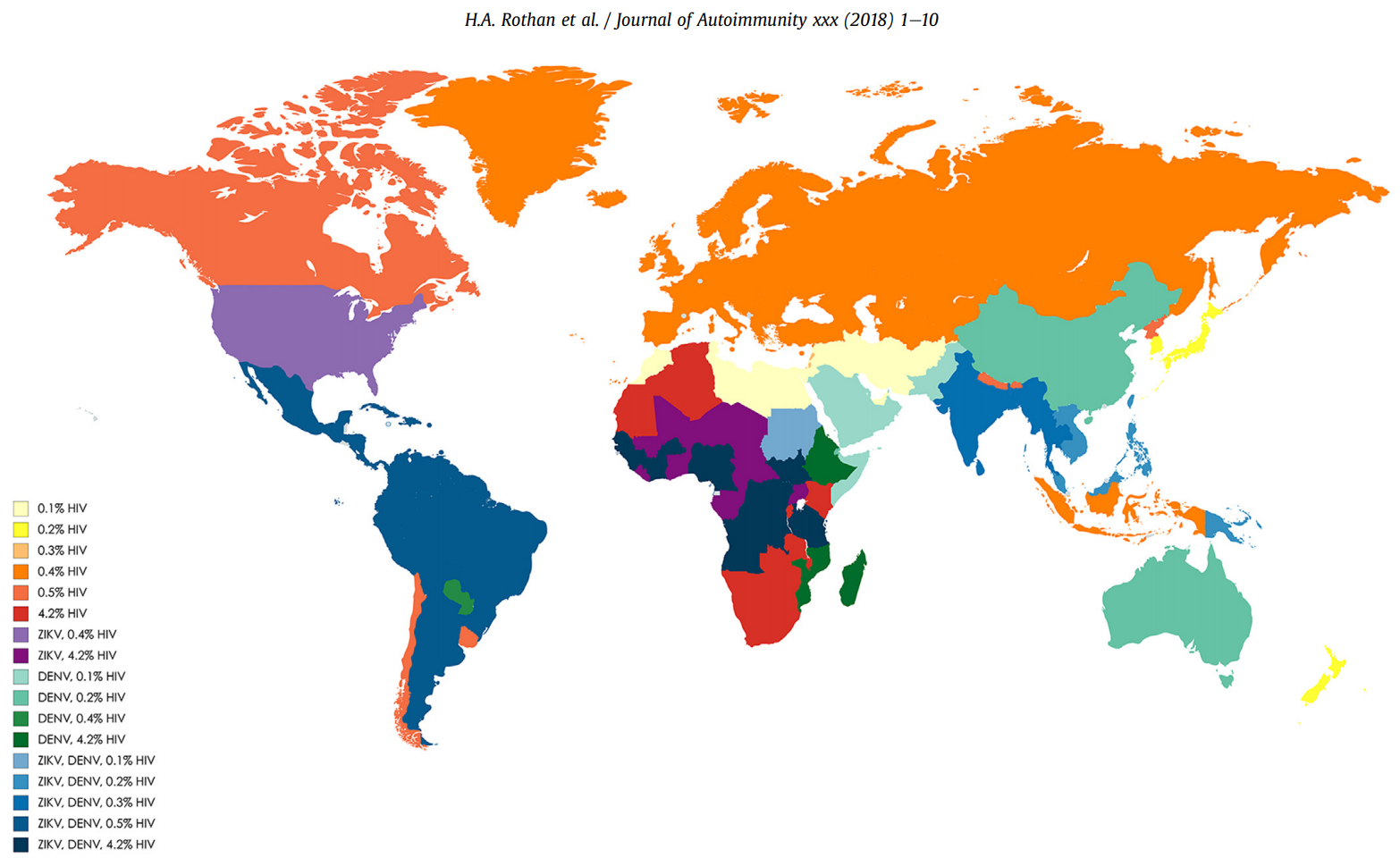
Como visualizar os dados?
CARTOGRAMAS
Singapore Zika Study Group. Outbreak of Zika virus infection in Singapore: an epidemiological, entomological, virological, and clinical analysis. Lancet Infect Dis. 2017 Aug;17(8):813-821. doi: 10.1016/S1473-3099(17)30249-9. Epub 2017 May 17.
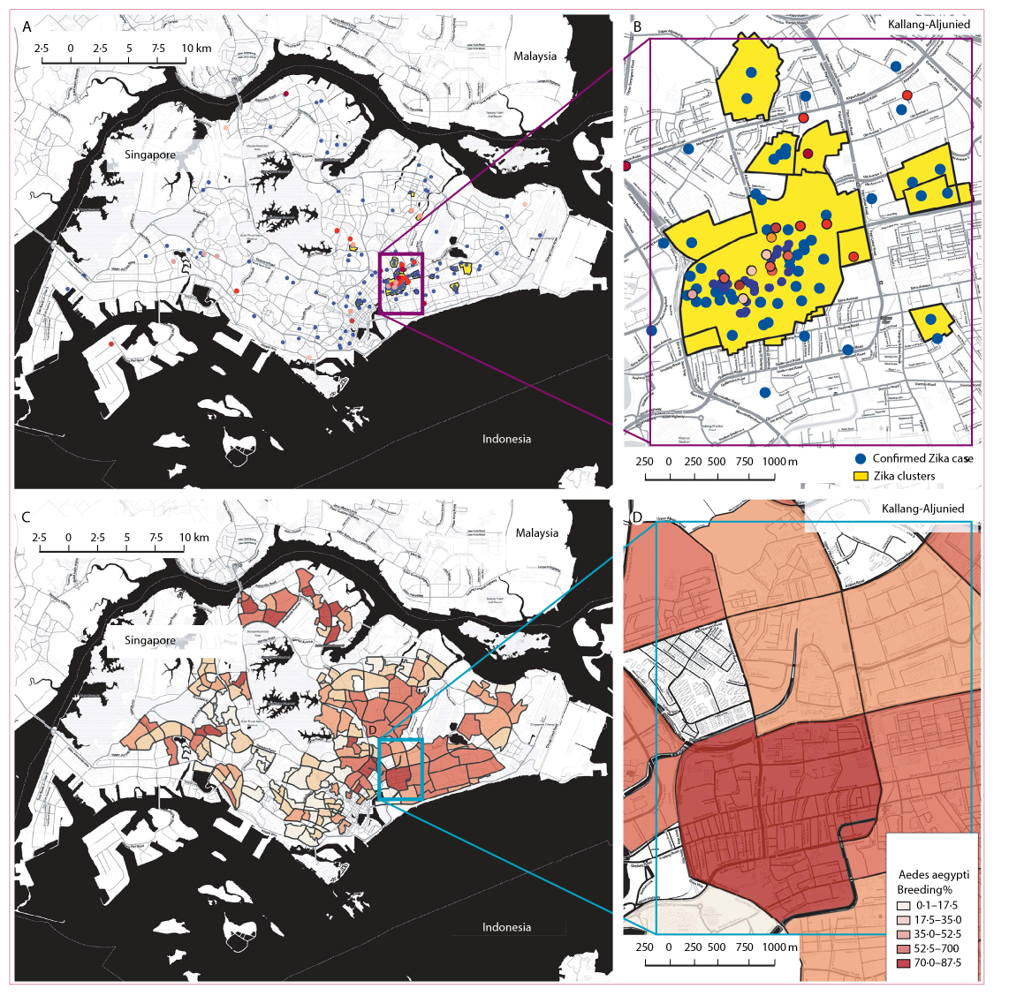
Como visualizar os dados?
CARTOGRAMAS
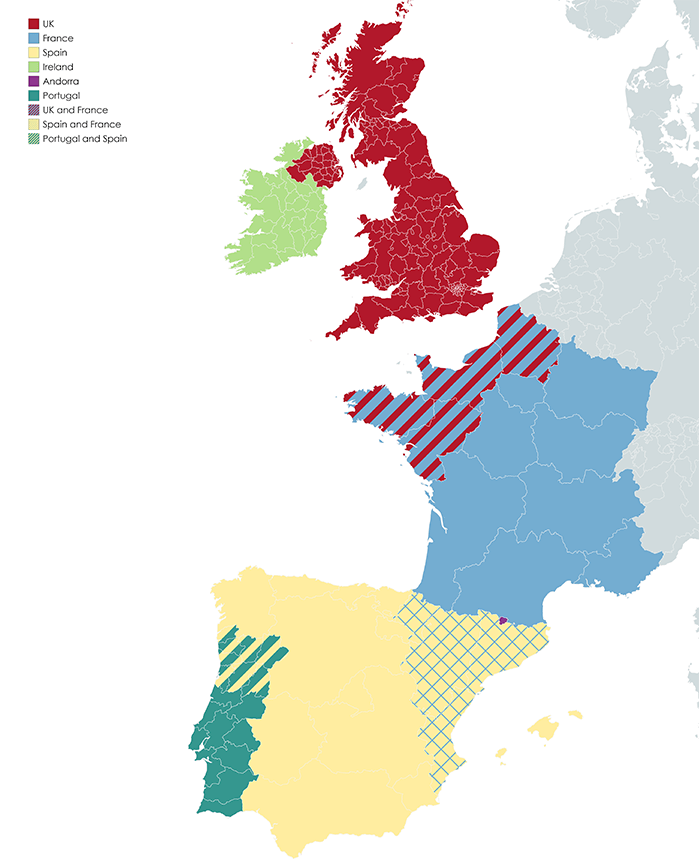
Como visualizar os dados?
GRÁFICO DE BARRAS
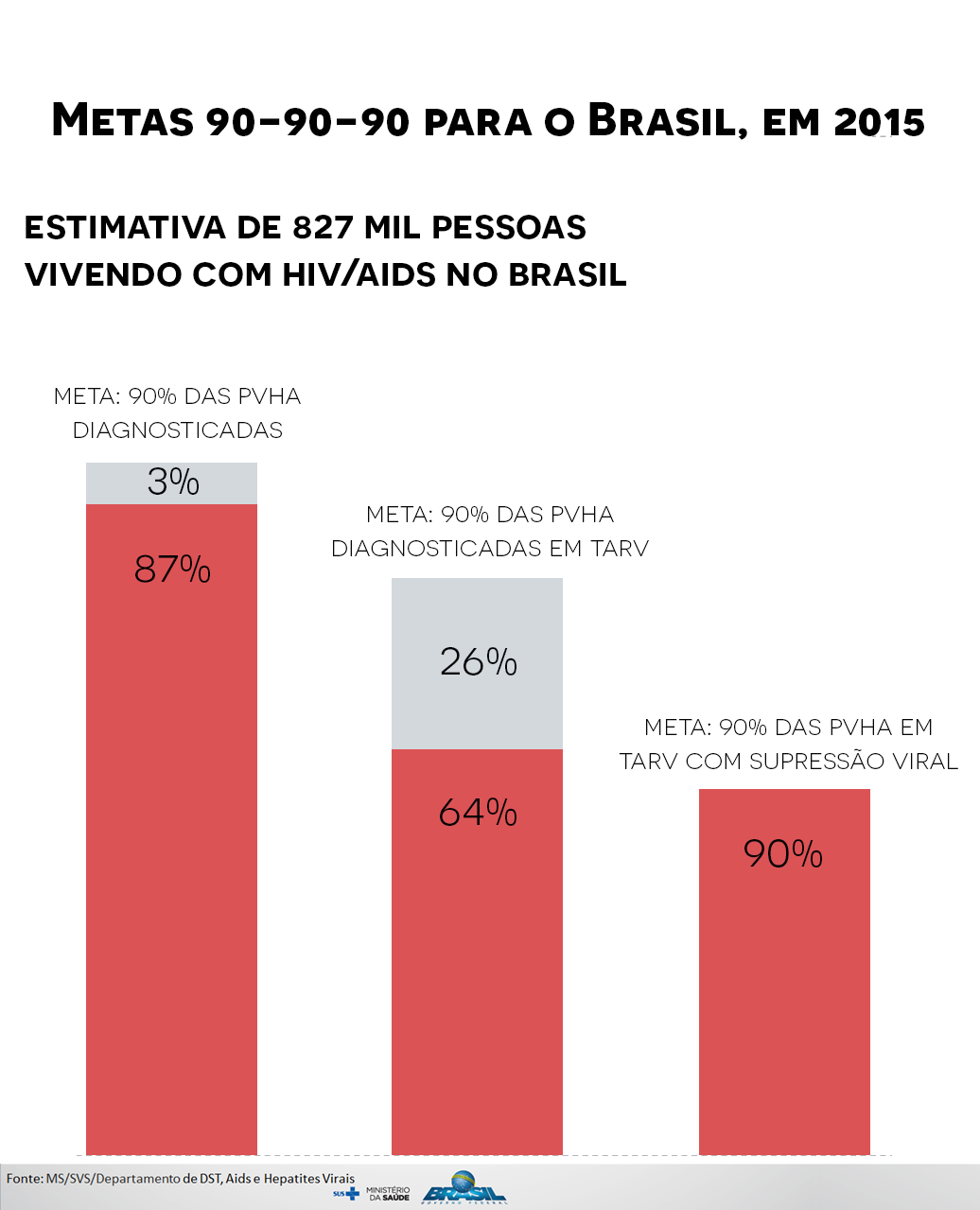
UNAIDS. Metas 90-90-90 – Gráfico. https://unaids.org.br/estatisticas/metas-90-90-90-grafico/
Como visualizar os dados?
Departamento de Doenças de Condições Crônicas e Infecções Sexualmente Transmissíveis. MINISTÉRIO DA SAÚDE. Boletim epidemiológico HIV/Aids 2018. http://www.aids.gov.br/pt-br
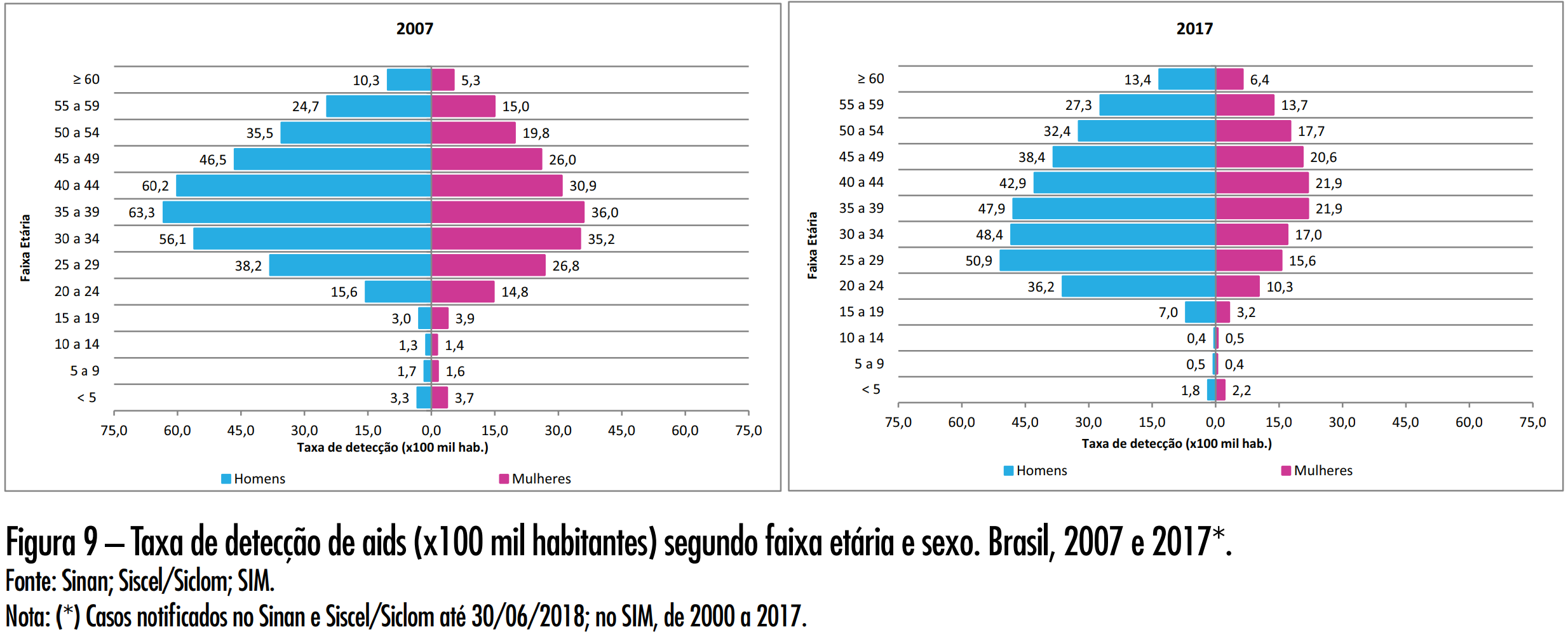
HISTOGRAMA
Como visualizar os dados?
Adaptado de: Maartens G1, Celum C2, Lewin SR3. HIV infection: epidemiology, pathogenesis, treatment, and prevention. Lancet. 2014 Jul 19;384(9939):258-71. doi: 10.1016/S0140-6736(14)60164-1. Epub 2014 Jun 5.
Karpinski J1,2, Hauber I2, Chemnitz J2, Schäfer C2,3, Paszkowski-Rogacz M1, Chakraborty D1, Beschorner N2, Hofmann-Sieber H2,3, Lange UC2,3,4, Grundhoff A2,3, Hackmann K5, Schrock E5, Abi-Ghanem J6, Pisabarro MT6, Surendranath V7, Schambach A8, Lindner C9, van Lunzen J2,3,10, Hauber J2,3, Buchholz F1,7. Directed evolution of a recombinase that excises the provirus of most HIV-1 primary isolates with high specificity. Nat Biotechnol. 2016 Apr;34(4):401-9. doi: 10.1038/nbt.3467. Epub 2016 Feb 22.
GRÁFICO DE LINHAS
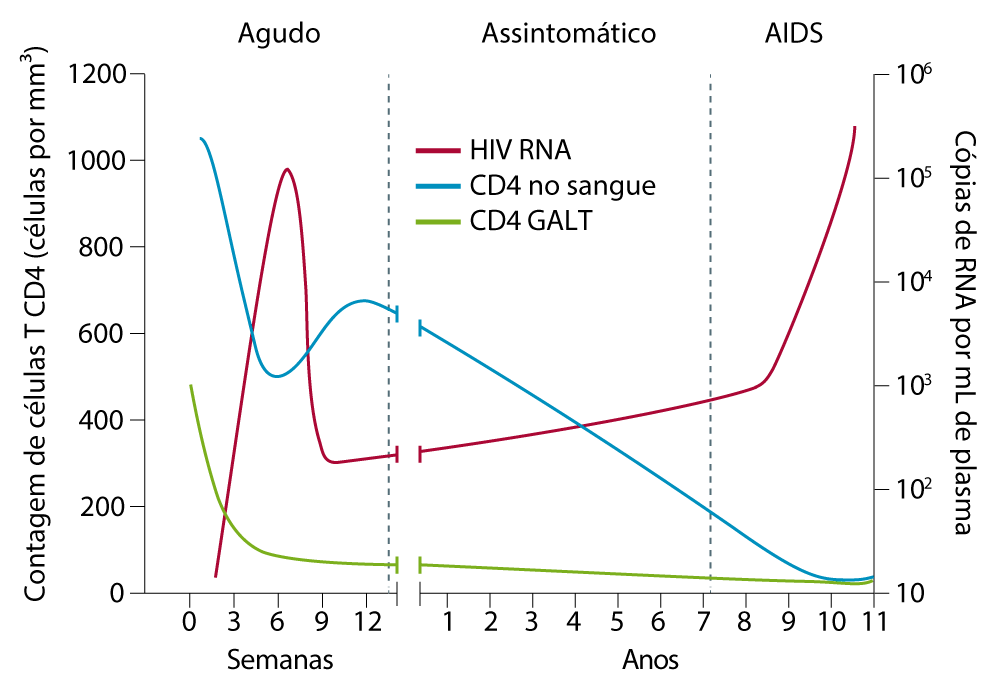
Curso da infeção por HIV-1 em indivíduos não tratados
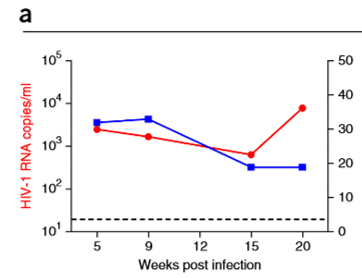
Como visualizar os dados?
GRÁFICO DE SETOR
Centers for Disease Control and Prevention (CDC). Basic Statistics. https://www.cdc.gov/hiv/basics/statistics.html?CDC_AA_refVal=https%3A%2F%2Fwww.cdc.gov%2Factagainstaids%2Fbasics%2Fstatistics.html
Fukutani KF1, Nascimento-Carvalho CM2, Van der Gucht W3, Wollants E3, Khouri R1, Dierckx T3, Van Ranst M3, Houspie L3, Bouzas ML4, Oliveira JR4, Barral A5, Van Weyenbergh J3, de Oliveira CI6. Pathogen transcriptional profile in nasopharyngeal aspirates of children with acute respiratory tract infection. J Clin Virol. 2015 Aug;69:190-6. doi: 10.1016/j.jcv.2015.06.005. Epub 2015 Jun 10.
New HIV Diagnoses in the United States and 6 Dependent Areas by Transmission Category, 2017
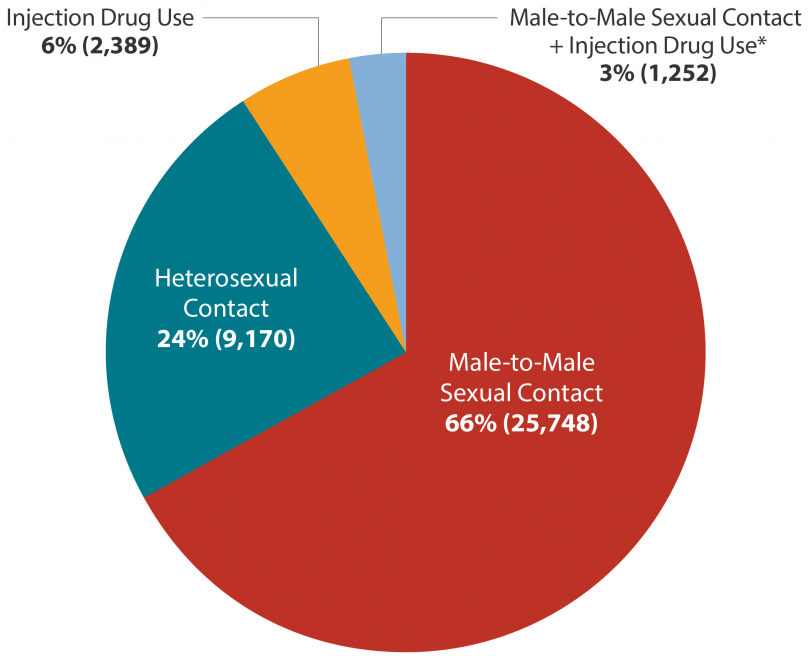
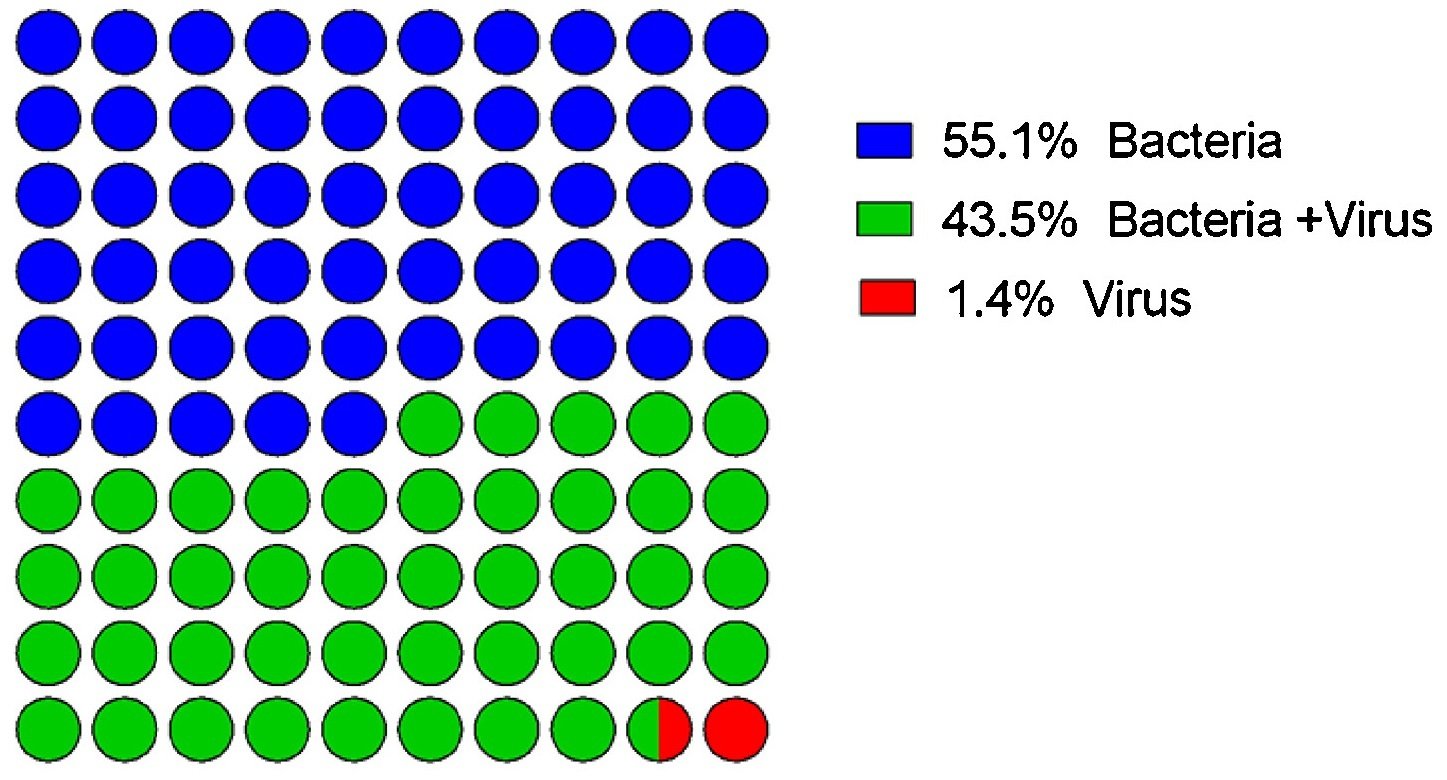
Fig. 4. Microbe counts (transcripts) in NPA of children with ARI, determined by nCounter.
Como visualizar os dados?
BOX-PLOT
Q2 / mediana / porcentil 50
média
Q1 (porcentil 25)
porcentil 10
porcentil 90
Q3 (porcentil 75)
porcentil 100 / máximo /extremo
porcentil 1 / mínimo / extremo
oulier
oulier
IQR
25%
75%
2 PARTES: MEDIANA
4 PARTES: QUARTIL
10 PARTES: DECIL
100 PARTES: PORCENTIL
Silvany Neto AM. Bioestatística sem segredos. Salvador: Edição do autor; 2008. p. 27-8.
Como visualizar os dados?
DIAGRAMA DE DISPERSÃO
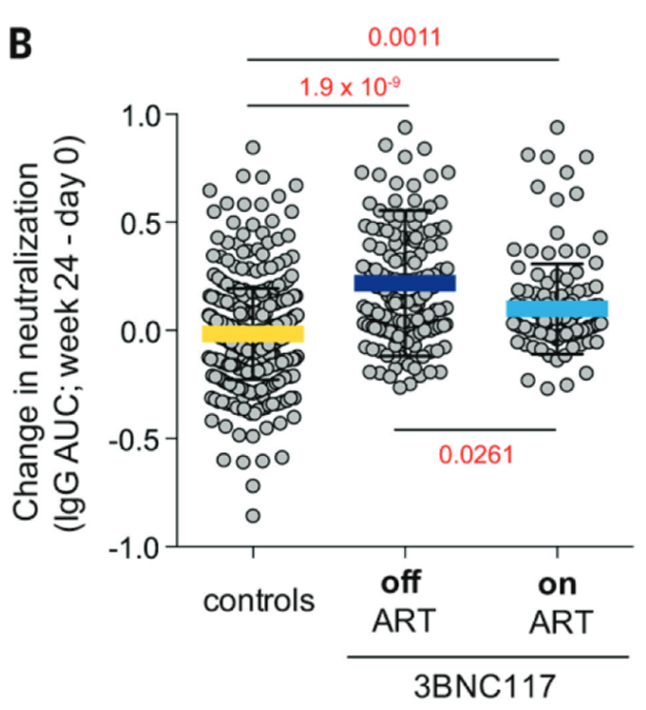
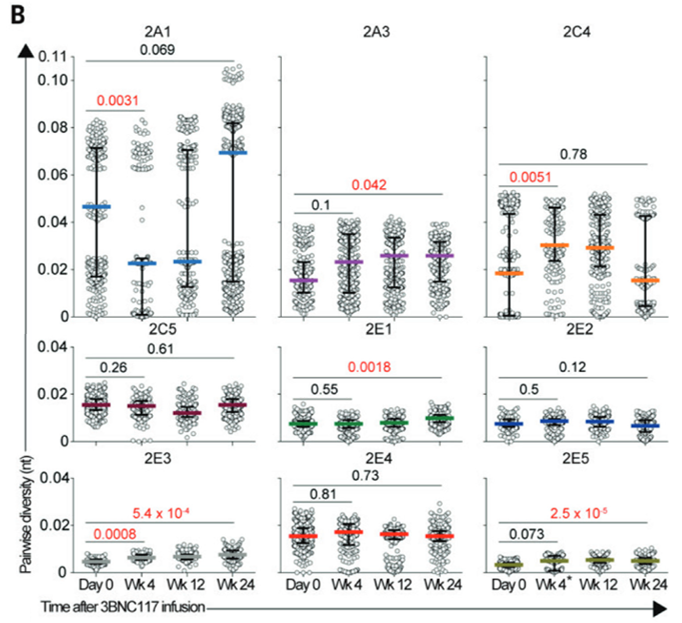
Schoofs T1, Klein F2, Braunschweig M3, Kreider EF4, Feldmann A5, Nogueira L1, Oliveira T1, Lorenzi JC1, Parrish EH4, Learn GH4, West AP Jr6, Bjorkman PJ6, Schlesinger SJ1, Seaman MS7, Czartoski J8, McElrath MJ8, Pfeifer N5, Hahn BH4, Caskey M1, Nussenzweig MC9. HIV-1 therapy with monoclonal antibody 3BNC117 elicits host immune responses against HIV-1. Science. 2016 May 20;352(6288):997-1001. doi: 10.1126/science.aaf0972. Epub 2016 May 5.
Como visualizar os dados?
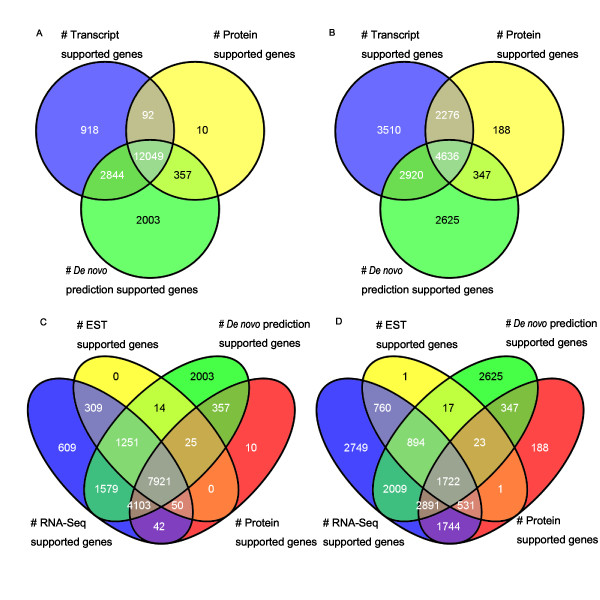
DIAGRAMA DE VENN
Li, Zhen & Zhang, Zhonghua & Yan, Pengcheng & Huang, Sanwen & Fei, Zhangjun & Lin, Kui. (2011). RNA-Seq improves annotation of protein-coding genes in the cucumber genome. BMC genomics. 12. 540. 10.1186/1471-2164-12-540.
Singapore Zika Study Group. Outbreak of Zika virus infection in Singapore: an epidemiological, entomological, virological, and clinical analysis. Lancet Infect Dis. 2017 Aug;17(8):813-821. doi: 10.1016/S1473-3099(17)30249-9. Epub 2017 May 17.
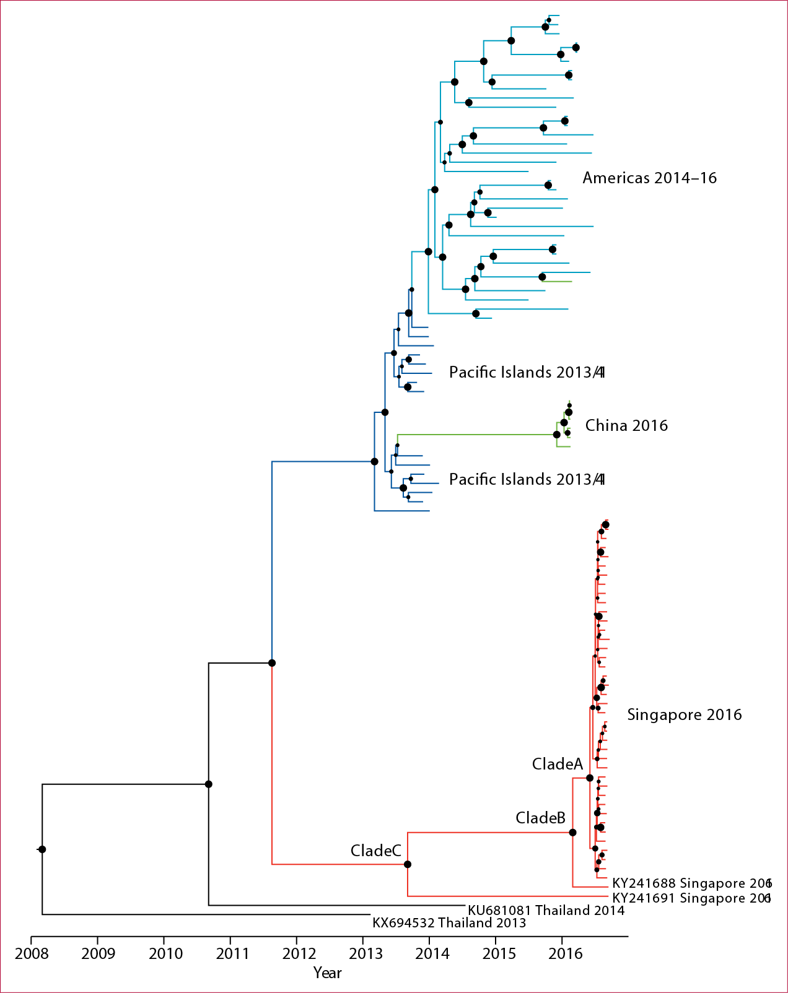
Como visualizar os dados?
CLADOGRAMA (FILOGRAMA)
Como visualizar os dados?
GRAFO (REDE)
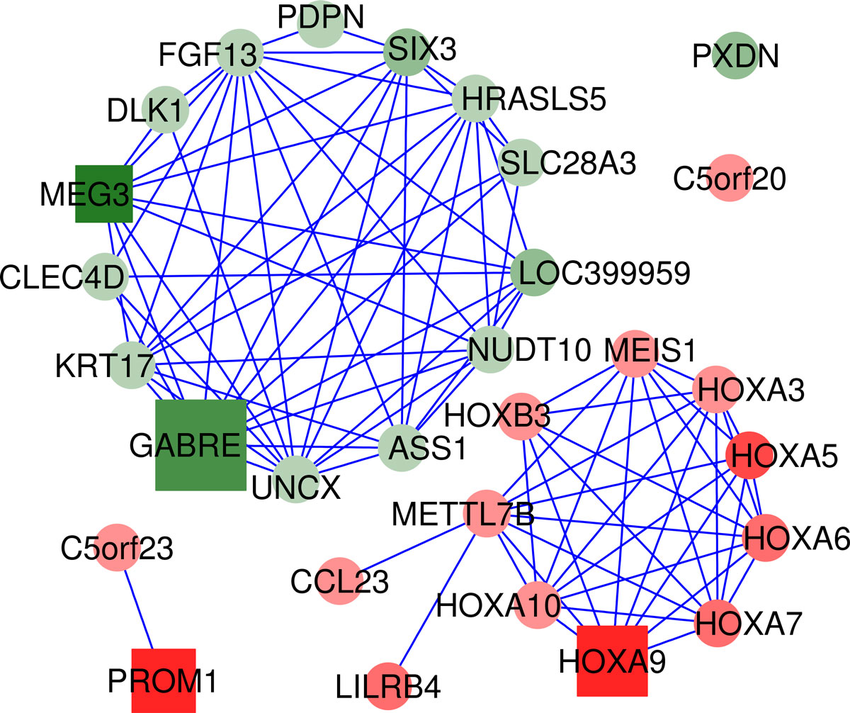
Aibar, Sara & Fontanillo, Celia & Droste, Conrad & Roson-Burgo, Beatriz & Campos-Laborie, Francisco & Hernández, Jesús & De Las Rivas, Javier. (2015). Analyse multiple disease subtypes and build associated gene networks using genome-wide expression profiles. BMC genomics. 16 Suppl 5. S3. 10.1186/1471-2164-16-S5-S3.
Como visualizar os dados?
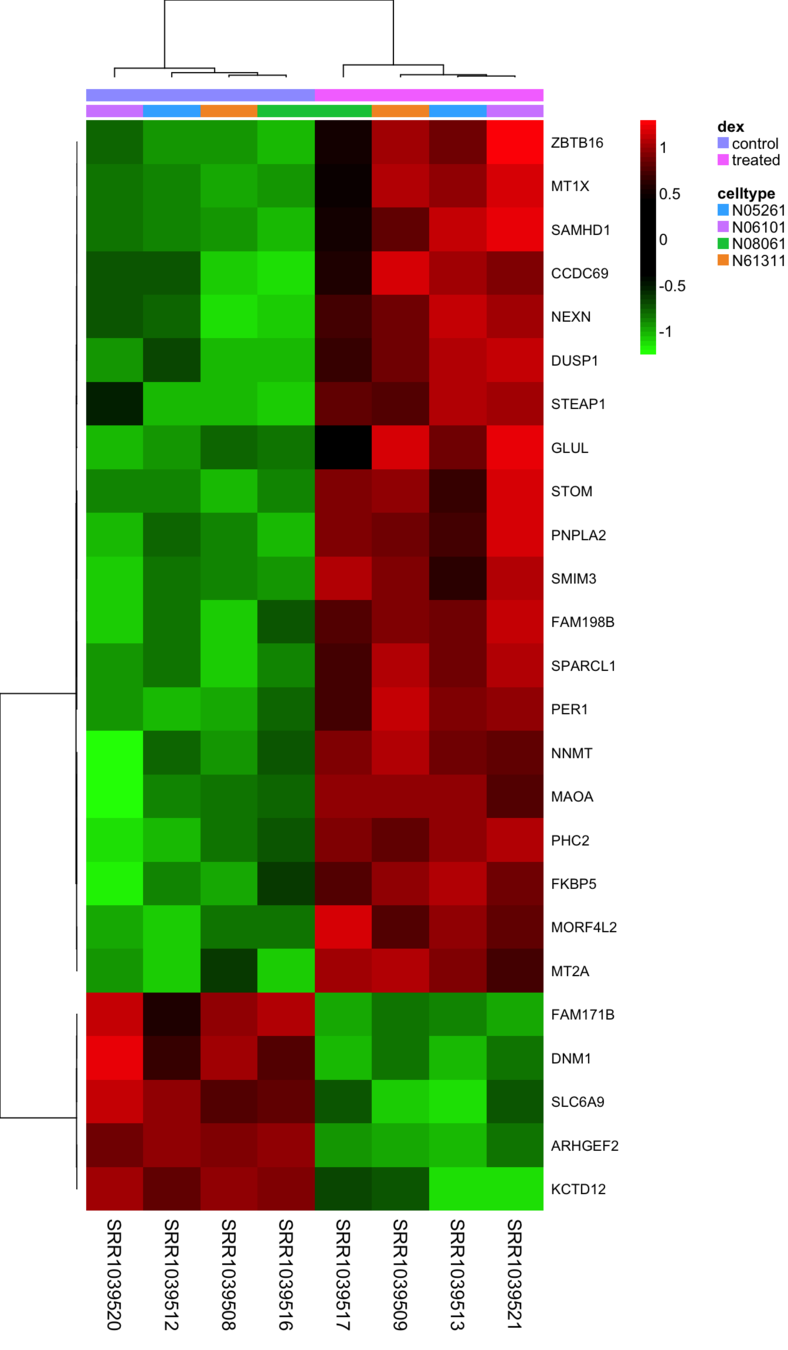
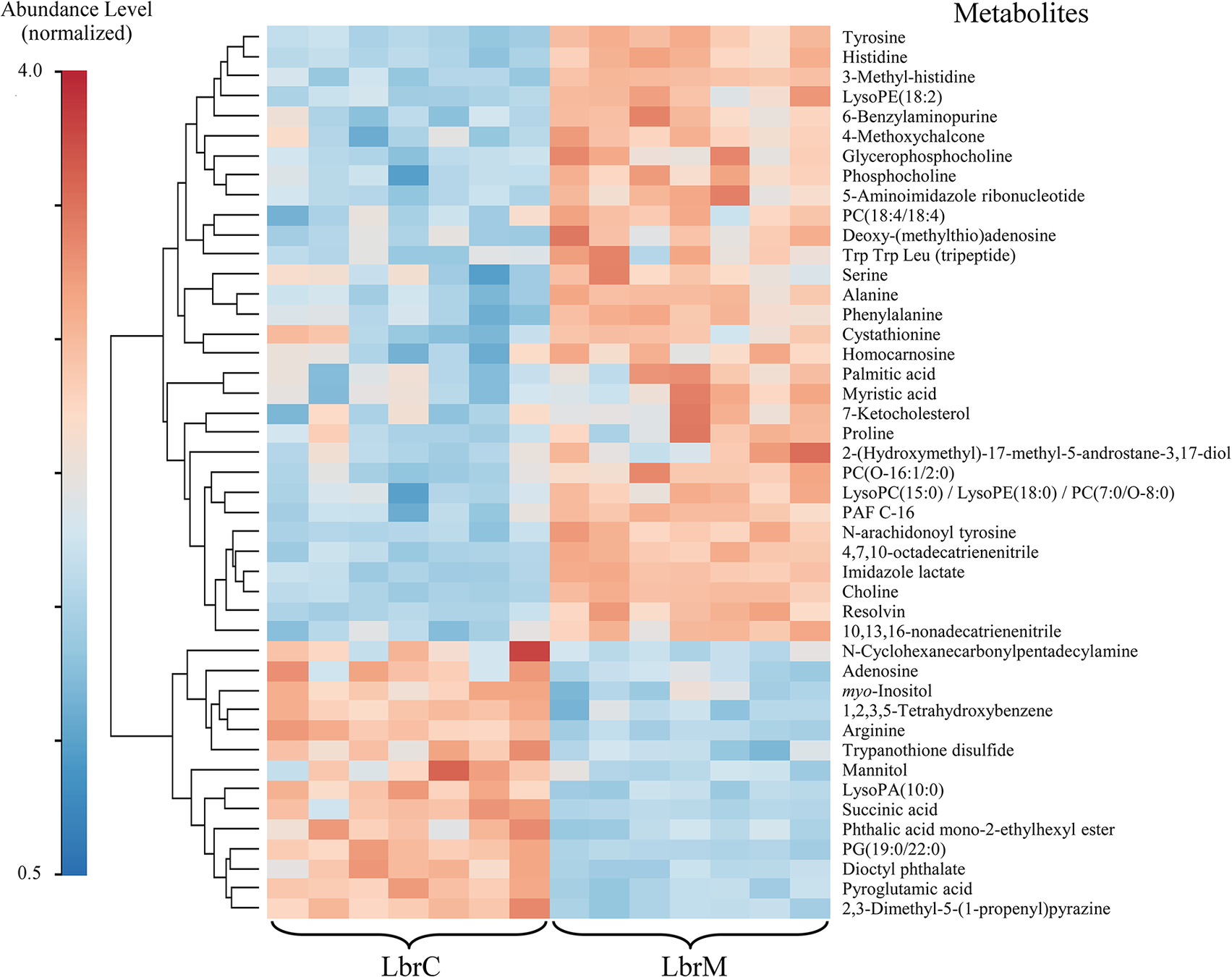
HEATMAP (MAPA DE CALOR)
Alves‐Ferreira, Eliza & de Toledo, Juliano & De Oliveira, Arthur & Ferreira, Tiago & Ruy, Patricia & Pinzan, Camila & F Santos, Ramon & Boaventura, Viviane & Rojo, David & Lopez, M.A. & Rosa, Jose & Barbas, Coral & Barral Netto, Manoel & Barral, Aldina & Cruz, Angela. (2015). Differential Gene Expression and Infection Profiles of Cutaneous and Mucosal Leishmania braziliensis Isolates from the Same Patient. PLoS Neglected Tropical Diseases. 9. 10.1371/journal.pntd.0004018.
E como os dados se distribuem?
DISTRIBUIÇÃO DE FREQUÊNCIAS
Como uma variável se comporta vai refletir em que tipo de análise podemos realizar
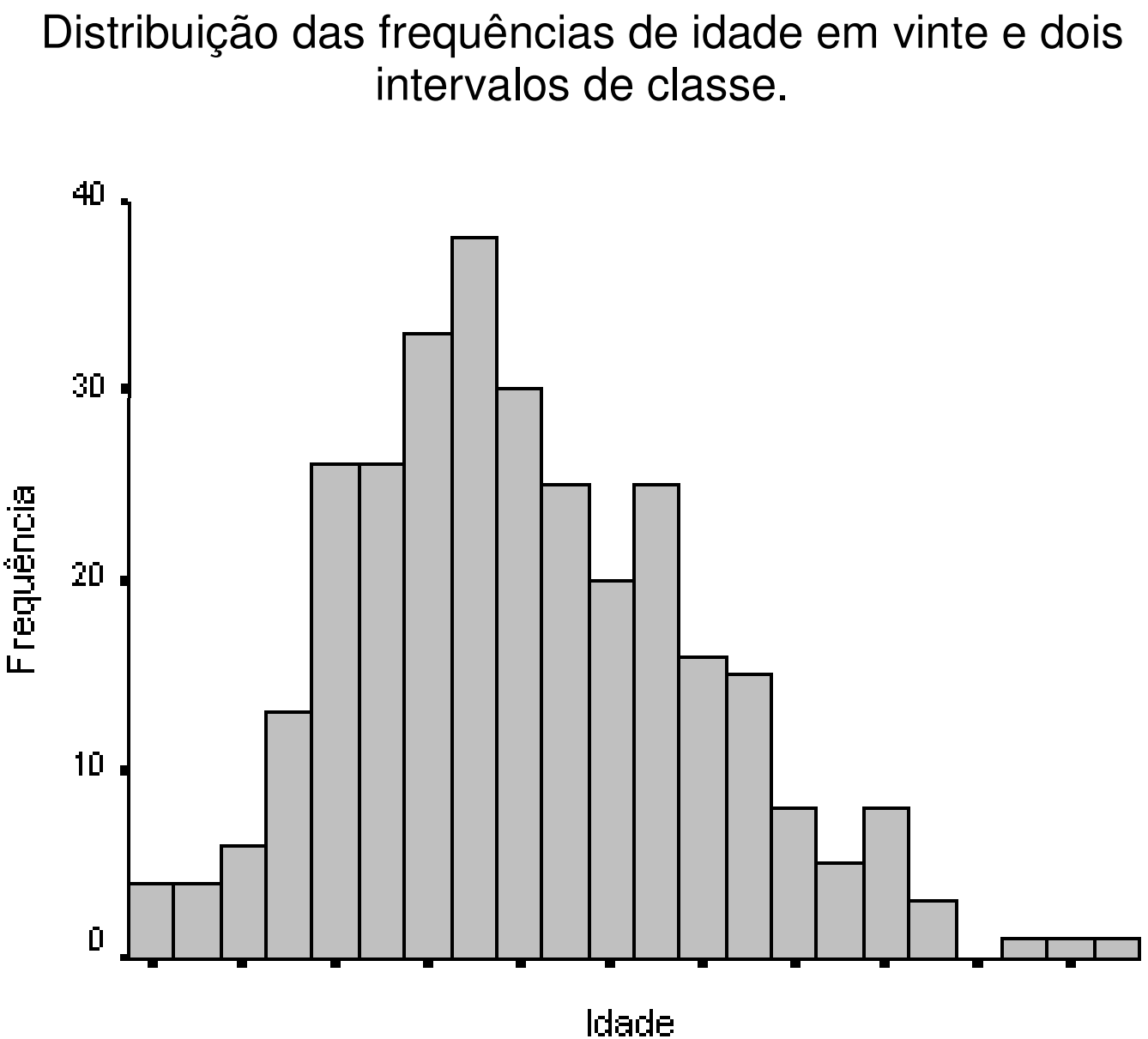
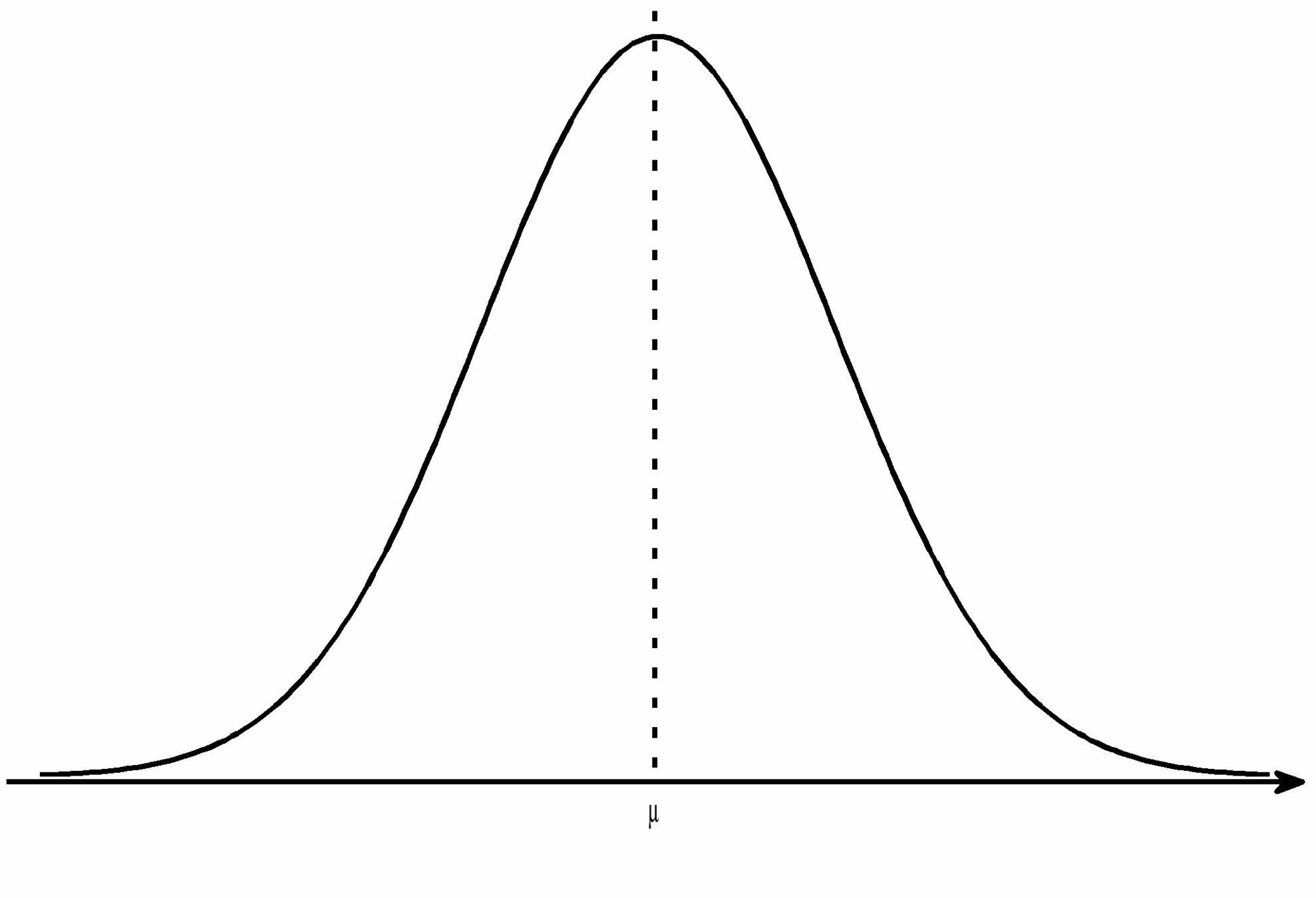
Silvany Neto AM. Bioestatística sem segredos. Salvador: Edição do autor; 2008. p. 27-8.
E como os dados se distribuem?
DISTRIBUIÇÃO DE FREQUÊNCIAS
Como uma variável se comporta vai refletir em que tipo de análise podemos realizar


A área da curva (a linha) equivale à probabilidade de ocorrência dos valores
Silvany Neto AM. Bioestatística sem segredos. Salvador: Edição do autor; 2008. p. 27-8.
E como os dados se distribuem?
DISTRIBUIÇÃO DE FREQUÊNCIAS
Como uma variável se comporta vai refletir em que tipo de análise podemos realizar


FREQUÊNCIA MAIS BAIXA PARA VALORES MAIS ALTOS E BAIXOS
FREQUÊNCIA MAIS ALTA PARA VALORES MAIS CENTRAIS
Silvany Neto AM. Bioestatística sem segredos. Salvador: Edição do autor; 2008. p. 27-8.
E como os dados se distribuem?
DISTRIBUIÇÃO DE FREQUÊNCIAS
Alguns estatísticos desenvolveram uma curva teórica para uma população infinita e com propriedades semelhantes, a qual pudesse ser utilizada com modelo para representar distribuições reais
O que é normal e o que é patológico?
Silvany Neto AM. Bioestatística sem segredos. Salvador: Edição do autor; 2008. p. 27-8.
E como os dados se distribuem?
DISTRIBUIÇÃO DE FREQUÊNCIAS
Alguns estatísticos desenvolveram uma curva teórica para uma população infinita e com propriedades semelhantes, a qual pudesse ser utilizada com modelo para representar distribuições reais
O que é normal e o que é patológico?
Silvany Neto AM. Bioestatística sem segredos. Salvador: Edição do autor; 2008. p. 27-8.
E como os dados se distribuem?
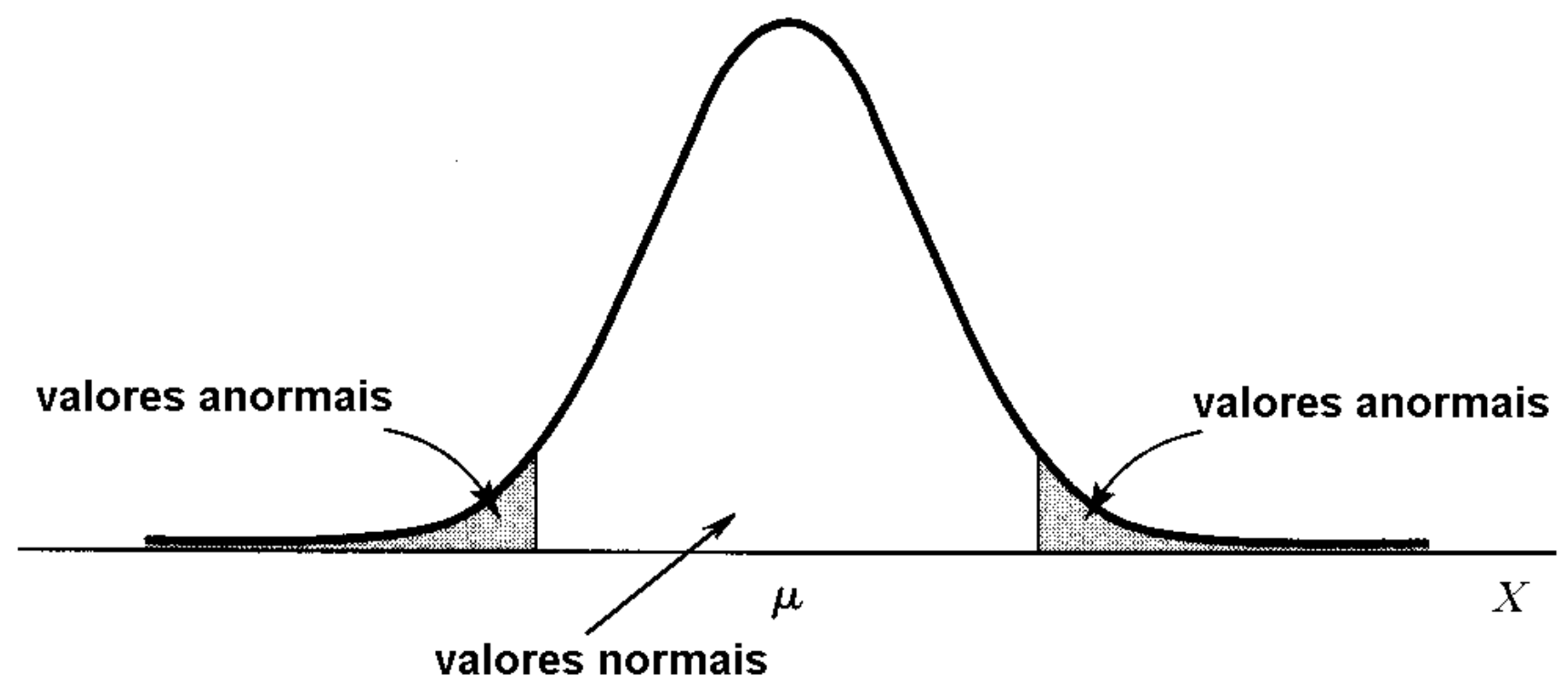
CRITÉRIO ESTATÍSTICO PARA DEFINIÇÃO DE NORMALIDADE

Limitações:
-
Nem todos os parâmetros biológicos indicativos de doença tem comportamento de distribuição normal
-
Se todos os valores abaixo ou acima de um limite estatístico fossem anormais, a prevalência de todas as doenças seria a mesma
-
As doenças não agem "sozinhas"
-
Nem sempre um valor fora do limite de referência é indicativo de patogenicidade
-
Nem sempre um valor dentro da referência reflete em normalidade
Por isto podemos discutir sobre uma variável alterada não é indicativo de doença!
Silvany Neto AM. Bioestatística sem segredos. Salvador: Edição do autor; 2008. p. 27-8.
Estatística
Inferencial
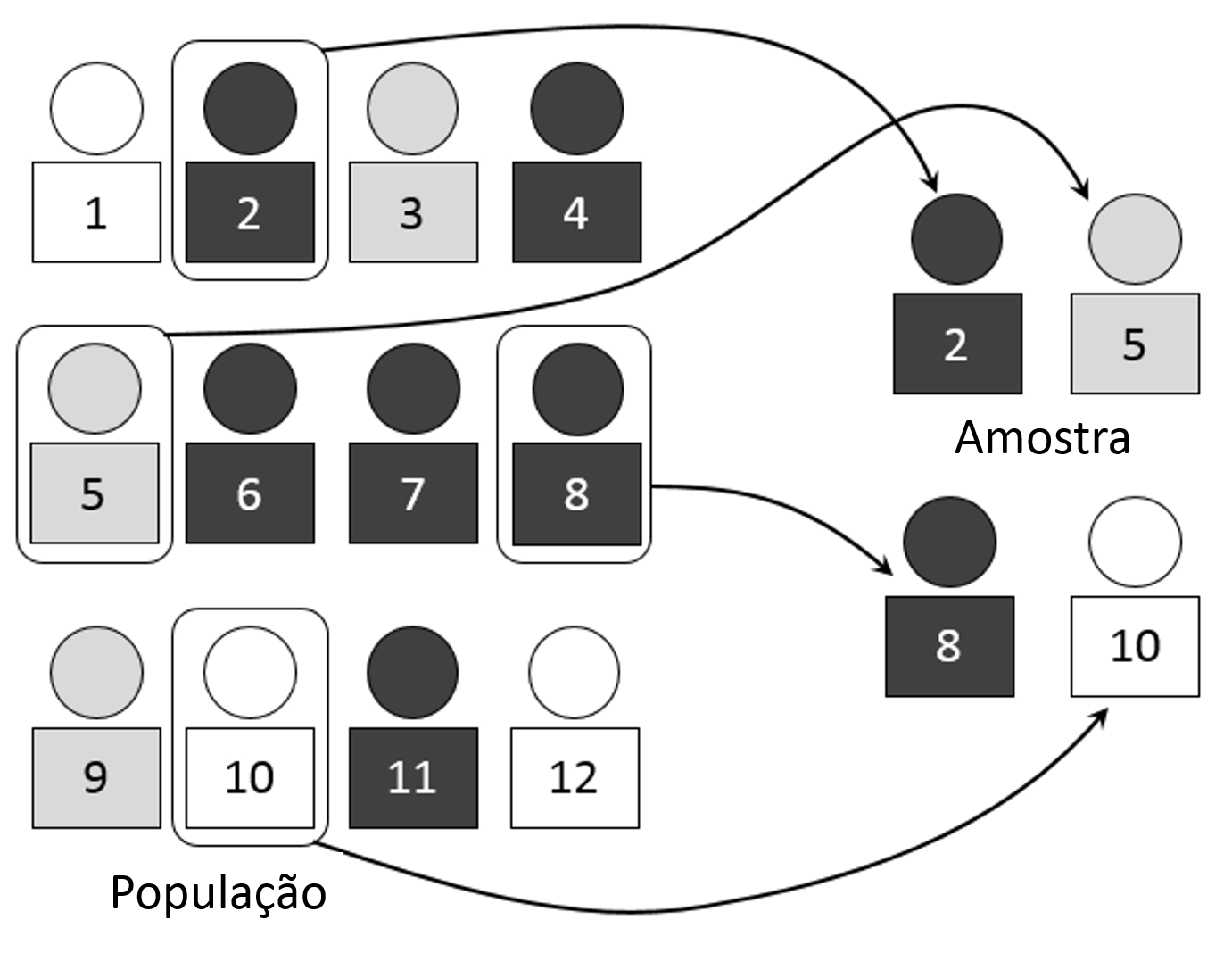
É um subconjunto de uma população, com tamanho suficientemente grande para suas características serem representativas para a população de origem
Amostra
É um conjunto de elementos com pelo menos uma característica em comum
População
Silvany Neto AM. Bioestatística sem segredos. Salvador: Edição do autor; 2008. p. 27-8.
Amostras
Como estudar sobre algo se não conseguimos estudar toda a população?
Pareadas:
-
Mesmo "indivíduo"
-
Duas observações em um mesmo "indivíduo" são mais prováveis de serem similares
Não pareadas:
-
"Indivíduos" são independentes
Silvany Neto AM. Bioestatística sem segredos. Salvador: Edição do autor; 2008. p. 27-8.
Amostragem
Identificação da população adequada
Método adequado de escolha dos indivíduos a serem estudados
Seleção de um número adequado de indivíduos
Como estudar sobre algo se não conseguimos estudar toda a população?
ETAPAS
1
2
3
Silvany Neto AM. Bioestatística sem segredos. Salvador: Edição do autor; 2008. p. 27-8.
Amostragem
ALEATÓRIA vs NÃO ALEATÓRIA
Aleatória:
-
Procedimentos controlados para seleção dos elementos
Não aleatória:
-
Por conveniência
-
Voluntária
Silvany Neto AM. Bioestatística sem segredos. Salvador: Edição do autor; 2008. p. 27-8.
Amostragem
ALEATÓRIA vs NÃO ALEATÓRIA
Para fins práticos:
-
Amostras grandes: n>100
-
Amostras médias: n>30
-
Amostras pequenas: n<30
-
Amostras muito pequenas n<12
Silvany Neto AM. Bioestatística sem segredos. Salvador: Edição do autor; 2008. p. 27-8.

Aleatória:
-
Procedimentos controlados para seleção dos elementos
Não aleatória:
-
Por conveniência
-
Voluntária
Comos analisamos variáveis?
A estatística inferencial é o processo pelo qual tiramos conclusões sobre uma população a partir de resultados em uma amostra aleatória
população
amostra
representativa
cria conclusões
Silvany Neto AM. Bioestatística sem segredos. Salvador: Edição do autor; 2008. p. 27-8.
Comos analisamos variáveis?
-
A primeira etapa de um teste estatístico é a definição do nível de significância estatística
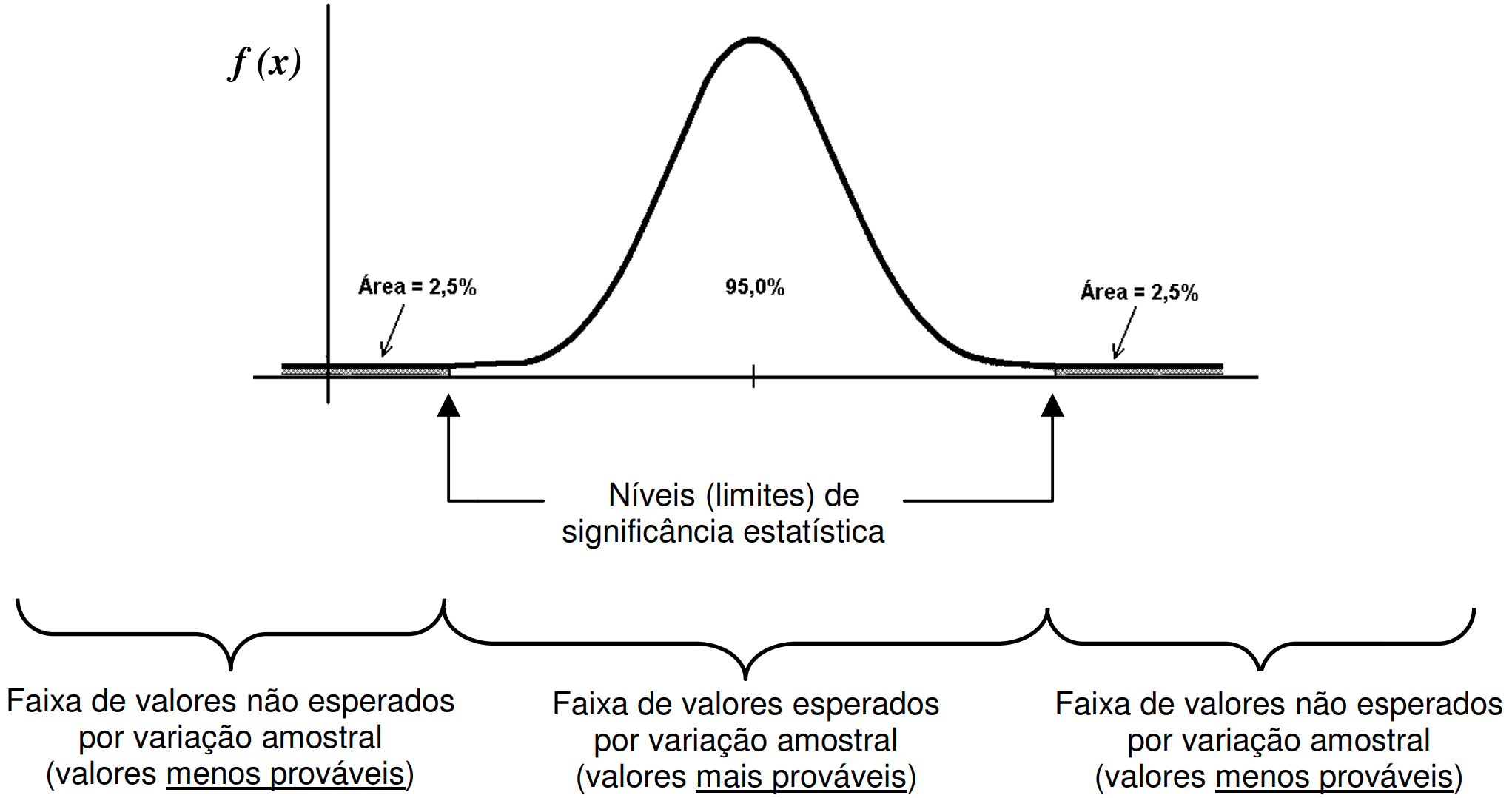
0,05 ou 5%
1
Silvany Neto AM. Bioestatística sem segredos. Salvador: Edição do autor; 2008. p. 27-8.
Comos analisamos variáveis?
0,01 ou 1%
-
A primeira etapa de um teste estatístico é a definição do nível de significância estatística
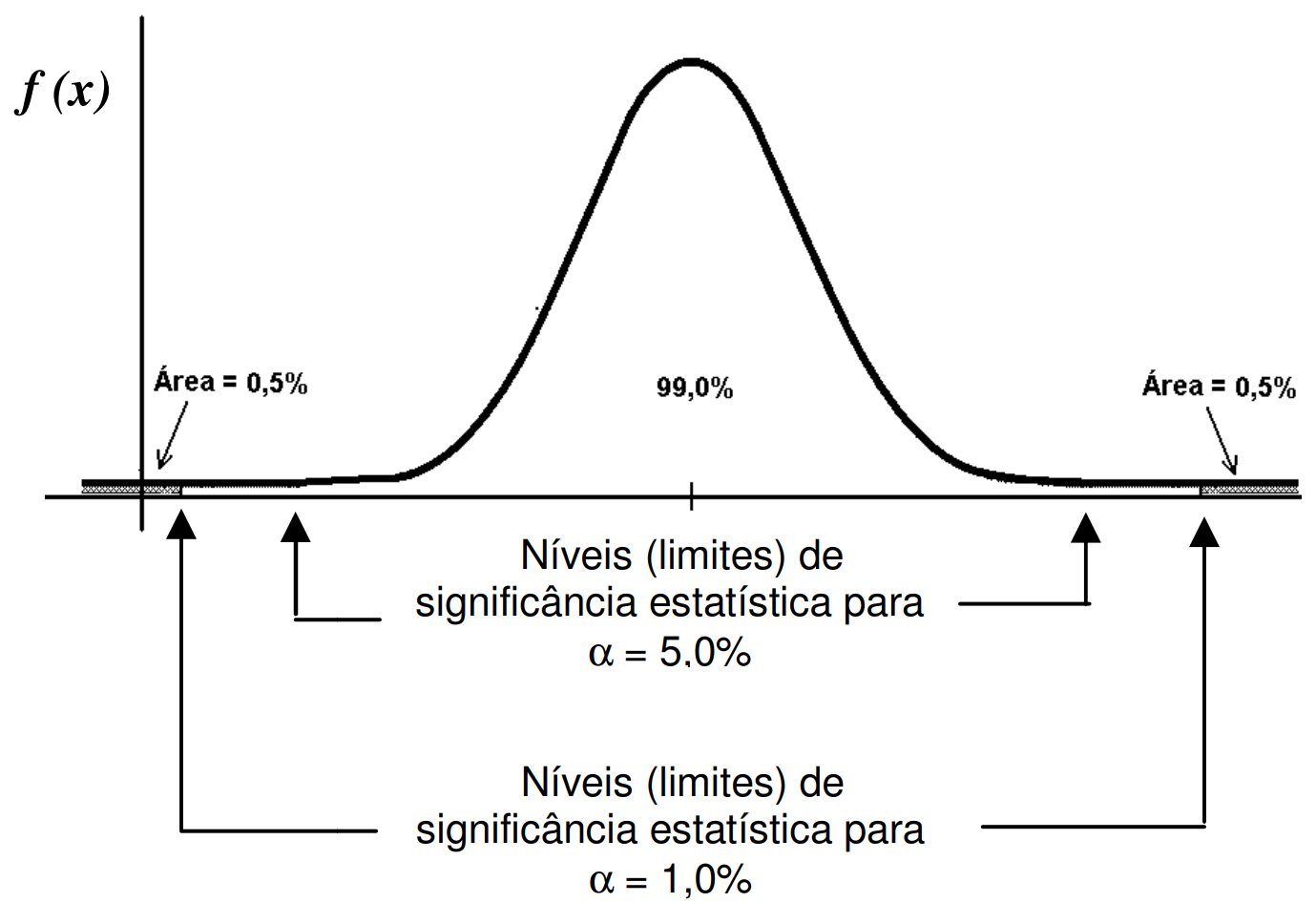
1
Silvany Neto AM. Bioestatística sem segredos. Salvador: Edição do autor; 2008. p. 27-8.
Comos analisamos variáveis?
0,09 ou 9%
-
A primeira etapa de um teste estatístico é a definição do nível de significância estatística
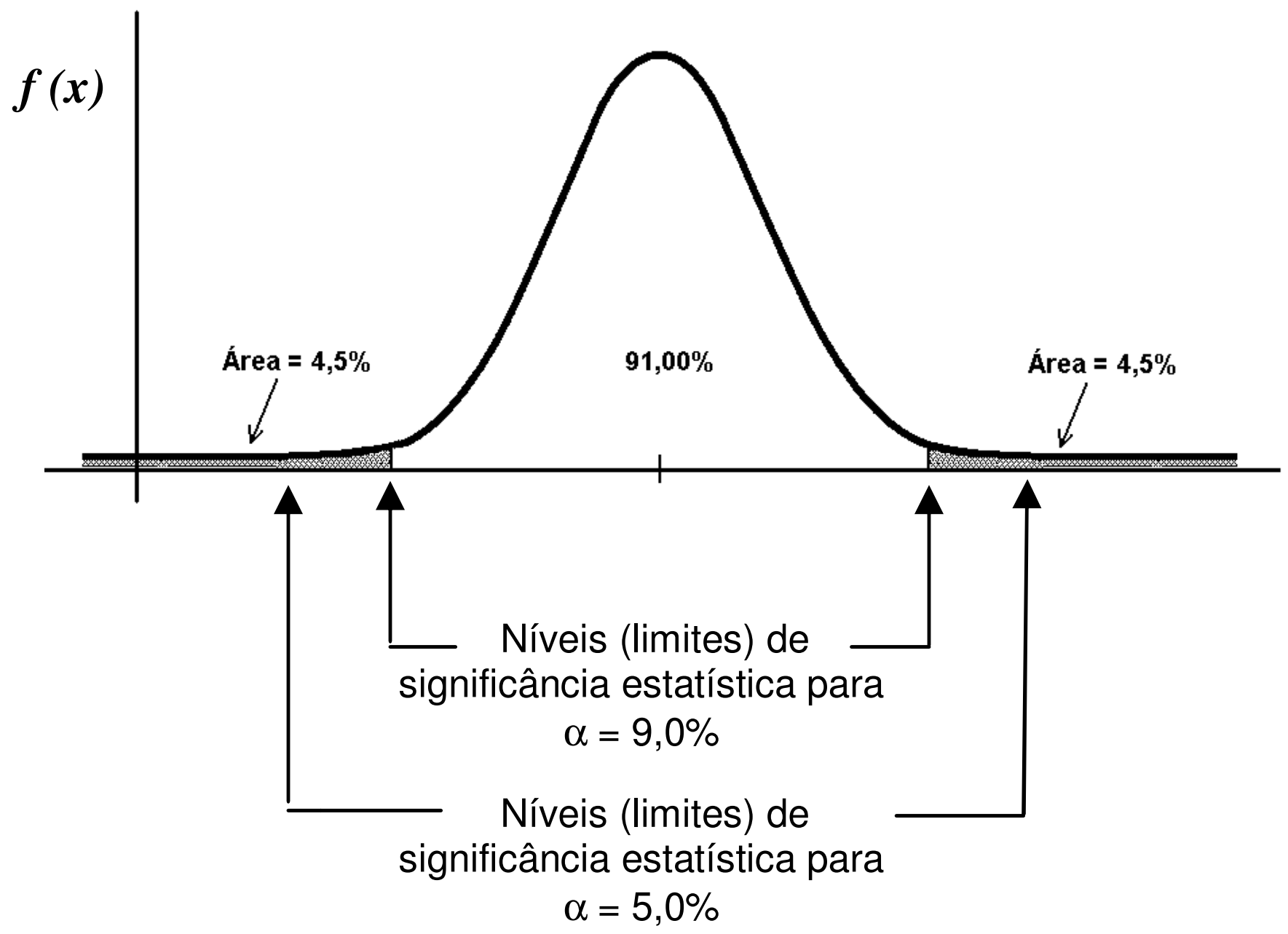
1
Silvany Neto AM. Bioestatística sem segredos. Salvador: Edição do autor; 2008. p. 27-8.
Comos analisamos variáveis?
-
Definimos as hipóteses estatísticas
-
Para cada teste estatístico, duas hipóteses são testadas:
-
Hipótese nula - HO - é aquela vigente e que afirma não ter diferenças entre o suposto problema
-
Hipótese alternativa - HA - é aquela levantada pelo estudo
-
2
Silvany Neto AM. Bioestatística sem segredos. Salvador: Edição do autor; 2008. p. 27-8.
Comos analisamos variáveis?
-
Definimos as hipóteses estatísticas
-
Para cada teste estatístico, duas hipóteses são testadas:
-
Hipótese nula - HO - é aquela vigente e que afirma não ter diferenças entre o suposto problema
-
Hipótese alternativa - HA - é aquela levantada pelo estudo
-
2
-
Definir os testes estatísticos apropriados
3
Silvany Neto AM. Bioestatística sem segredos. Salvador: Edição do autor; 2008. p. 27-8.
Comos analisamos variáveis?
-
Definimos as hipóteses estatísticas
-
Para cada teste estatístico, duas hipóteses são testadas:
-
Hipótese nula - HO - é aquela vigente e que afirma não ter diferenças entre o suposto problema
-
Hipótese alternativa - HA - é aquela levantada pelo estudo
-
2
-
Definir os testes estatísticos apropriados
3
-
Analisar os dados
4
Silvany Neto AM. Bioestatística sem segredos. Salvador: Edição do autor; 2008. p. 27-8.
Comos analisamos variáveis?
Existem dois erros possíveis envolvidos na inferência estatística:
| Conclusão do teste | É verdadeira | É falsa |
|---|---|---|
| Aceitação de HO | Conclusão correta | Erro tipo II |
| Rejeição de HO | Erro tipo I | Conclusão correta |
| Realidade sobre HO |
|---|
Quando definimos um valor significante, estamos limitando a probabilidade de o erro tipo I ocorrer
O erro tipo II por convenção tem uma probabilidade estipulada em 20%
erro menos grave
Silvany Neto AM. Bioestatística sem segredos. Salvador: Edição do autor; 2008. p. 27-8.
Quais testes utilizamos?
TESTES PARAMÉTRICOS vs NÃO PARAMÉTRICOS
Paramétricos:
-
Utilizam em seu algoritmo o desvio padrão e média
-
ANOVA: utiliza variância
Silvany Neto AM. Bioestatística sem segredos. Salvador: Edição do autor; 2008. p. 27-8.
Paramétricos:
-
Não são baseados nos critérios de uma população com distribuição normal
-
Também utilizados em amostras pequenas
-
Utilizam em seu algoritmo a mediana
São realizados pré testes para saber qual a distribuição da variável: Kolmogorov-Smirnov e Shapiro-Wilks
Quais testes utilizamos?
TESTES NÃO PARAMÉTRICOS
Silvany Neto AM. Bioestatística sem segredos. Salvador: Edição do autor; 2008. p. 27-8.
Se não utiliza desvio padrão e média, como funcionam?
| G1 |
|---|
| 3 |
| 45 |
| 102 |
| 10 |
| 13 |
| 12 |
| 5 |
| G2 |
|---|
| 4 |
| 7 |
| 89 |
| 102 |
| 5 |
| 5 |
| 11 |
Quais testes utilizamos?
TESTES NÃO PARAMÉTRICOS
Silvany Neto AM. Bioestatística sem segredos. Salvador: Edição do autor; 2008. p. 27-8.
Se não utiliza desvio padrão e média, como funcionam?
| G1 |
|---|
| 3 |
| 45 |
| 102 |
| 10 |
| 13 |
| 12 |
| 5 |
| G2 |
|---|
| 4 |
| 7 |
| 89 |
| 102 |
| 5 |
| 5 |
| 11 |
| G1 | Posição |
|---|---|
| 3 | 1 |
| 45 | 11 |
| 102 | 13 |
| 10 | 7 |
| 13 | 10 |
| 12 | 9 |
| 5 | 3 |
| G2 | Posição |
|---|---|
| 4 | 2 |
| 7 | 6 |
| 89 | 12 |
| 102 | 14 |
| 5 | 4 |
| 5 | 5 |
| 11 | 8 |
1. Transforma os valores em posições
Quais testes utilizamos?
TESTES NÃO PARAMÉTRICOS
Silvany Neto AM. Bioestatística sem segredos. Salvador: Edição do autor; 2008. p. 27-8.
Se não utiliza desvio padrão e média, como funcionam?
1. Transforma os valores em posições
| G1 |
|---|
| 3 |
| 45 |
| 102 |
| 10 |
| 13 |
| 12 |
| 5 |
| G2 |
|---|
| 4 |
| 7 |
| 89 |
| 102 |
| 5 |
| 5 |
| 11 |
| G1 | Posição |
|---|---|
| 3 | 1 |
| 45 | 11 |
| 102 | 13,5 |
| 10 | 7 |
| 13 | 10 |
| 12 | 9 |
| 5 | 4 |
| G2 | Posição |
|---|---|
| 4 | 2 |
| 7 | 6 |
| 89 | 12 |
| 102 | 13,5 |
| 5 | 4 |
| 5 | 4 |
| 11 | 8 |
Havendo empate nos valores, o rank será a média da soma dos ranks
(3+4+5)/3=12/3=4
(13+14)/2=27/2=13,5
Quais testes utilizamos?
TESTES NÃO PARAMÉTRICOS
Silvany Neto AM. Bioestatística sem segredos. Salvador: Edição do autor; 2008. p. 27-8.
2. A partir disto, pode-se obter a média e o desvio padrão
3. O algoritmos dos testes não paramétricos então utilizam estes valores de posição
4. O valores extremos não exercem grande impacto nas comparações
Quais testes utilizamos?
TESTES NÃO PARAMÉTRICOS
Silvany Neto AM. Bioestatística sem segredos. Salvador: Edição do autor; 2008. p. 27-8.
2. A partir disto, pode-se obter a média e o desvio padrão
3. O algoritmos dos testes não paramétricos então utilizam estes valores de posição
4. O valores extremos não exercem grande impacto nas comparações
Quais testes utilizamos?
TESTES NÃO PARAMÉTRICOS
Silvany Neto AM. Bioestatística sem segredos. Salvador: Edição do autor; 2008. p. 27-8.
2. A partir disto, pode-se obter a média e o desvio padrão
3. O algoritmos dos testes não paramétricos então utilizam estes valores de posição
4. O valores extremos não exercem grande impacto nas comparações
Quais testes utilizamos?

Quais pacotes estatísticos posso usar?
CLIQUE NA IMAGEM PARA IR NOS SITES
MICROSOFT OFFICE EDUCATION
MICROSOFT OFFICE EDUCATION


MICROSOFT OFFICE EDUCATION




Desenhos de pesquisa
Que tipo de desenho de estudo devo utilizar?

Ensaio clínico:
-
Testa o efeito de uma intervenção
-
Por motivos éticos, é pouco utilizada para investigar o fenômeno saúde-doenca
-
Atualmente mais utilizada para avaliação de eficácia-efetividade de terapias ou preventivas
-
Utiliza a estratégia de comparação de grupos (grupo com intervenção vs sem a intervenção)
ESTUDO EXPERIMENTAL
Ensaio Populacional:
-
Muito similar ao ensaio clínico, porém à nível populacional
Que tipo de desenho de estudo devo utilizar?
ESTUDO OBSERVACIONAL
Coorte:
-
Não interfere no evento estudado
-
Neste modelo, partimos da exposição de algo para o efeito na população de estudo
-
Pode ser prospectivo ou retrospectivo (eventos que ocorreram no passado)
Caso-controle:
-
Não interfere no evento estudado
-
Partimos do efeito encontrado para definir qual a exposição foi a responsável pela problemática
-
Sempre prospectivo (passagem de tempo crescente)
-
Utiliza indivíduos controles no estudo (pareamento)
Que tipo de desenho de estudo devo utilizar?
ESTUDO OBSERVACIONAL
Ecológico:
-
Não interfere no evento estudado
-
São utilizadas populaçoes geograficamente definidas
-
A mensuração do evento ocorre em um único momento temporal
-
Pode observar a exposição e o efeito ao mesmo tempo em que ocorrem
Séries temporais:
-
Não interfere no evento estudado
-
São utilizadas populaçoes geograficamente definidas
-
A mensuração do evento pode ocorrer em vários momentos temporais da mesma população
-
Pode observar a exposição e o efeito ao mesmo tempo em que ocorrem
Que tipo de desenho de estudo devo utilizar?
ESTUDO OBSERVACIONAL
Falácia ecológica: uma associação encontrada em uma população não implica necessariamente que a associação ocorra à nível individual
Séries temporais:
-
Não interfere no evento estudado
-
São utilizadas populaçoes geograficamente definidas
-
A mensuração do evento pode ocorrer em vários momentos temporais da mesma população
-
Pode observar a exposição e o efeito ao mesmo tempo em que ocorrem
Ecológico:
-
Não interfere no evento estudado
-
São utilizadas populaçoes geograficamente definidas
-
A mensuração do evento ocorre em um único momento temporal
-
Pode observar a exposição e o efeito ao mesmo tempo em que ocorrem
Que tipo de desenho de estudo devo utilizar?
Qual o melhor desenho de estudo?

Que tipo de desenho de estudo devo utilizar?

Que tipo de desenho de estudo devo utilizar?
Qual a pergunta do estudo?
Que tipo de desenho de estudo devo utilizar?
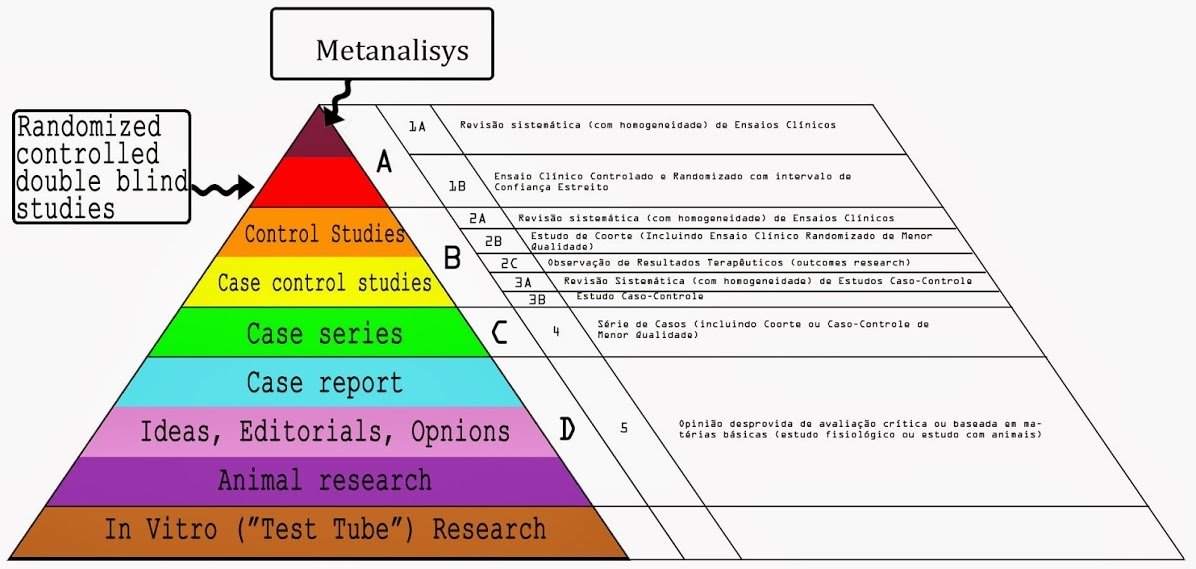
ESCALA DE EVIDENCIA CIENTÍFICA
Atividade 1
De forma lúdica construa um trabalho "científico" e defenda ele. Ele deve conter uma justificativa demonstrando a necessidade do estudo, o objetivo, como foram selecionados os dados e analisados (medotodologia) e os resultados encontrados (4,0 pontos).
A construção deve ser realizada em equipes de pelo menos 5 pessoas.
Atividade 2
Selecione um artigo científico e a partir dele, construa uma crítica e exemplificando de qual outro modo os resultados do estudo seriam melhor apresentados (3,0 pontos).
Além disto, pontue com outros trabalhos científicos se o achado do estudo pode realmente ser generalizado para outra população (3,0 pontos).
PRAZO: 30/09/2019
laisepaixao@gmail.com
BÁSICAS
FLETCHER, R. H.; FLETCHER, S. W.; FLETCHER, G. S. Epidemiologia Clínica: Elementos Essenciais. 5. ed. Porto Alegre: ArtMed, 2014.
GREENBERG, R. S. et al. Epidemiologia Clínica. 3. ed. Porto Alegre: ArtMed, 2004.
GURGE, M.; ROUQUAYROL, M. Z. Epidemiologia e Saúde. 8. ed. Rio de Janeiro: Medbook, 2018.
PEREIRA, M. G. Epidemiologia: Teoria e Prática. 1. ed. Rio de Janeiro: Guanabara Koogan, 1995.
SILVA, C. N. N. DA; PORTO, M. D. Metodologia Científica Descomplicada. 1. ed. Brasília: IFB, 2016.
SILVANY NETO, A. M. Bioestatística sem Segredos. 1. ed. Salvador: Annibal Muniz Silvany Neto, 2008.
VIEIRA, S. Introdução à Bioestatística. 4. ed. Rio de Janeiro: Elsevier, 2011.
COMPLEMENTARES
ALVES, R. Filosofia da Ciência: Introdução ao Jogo e a suas Regras. 10. ed. São Paulo: Loyola, 2005.
CHALMERS, A. F. O que é Ciência Afinal? 1. ed. São Paulo: Brasiliense, 1993.
CHALMERS, A. F. A Fabricação da Ciência. 1. ed. São Paulo: UNESP, 1994.
HUFF, D. Como Mentir com Estatística. 1. ed. Rio de Janeiro: Intrínseca, 2016.
HULLEY, S. B. et al. Delineando a Pesquisa Clínica: Uma Abordagem Epidemiológica. 4. ed. Porto Alegre: ArtMed, 2015.
LAVILLE, C.; DIONNE, J. A Construção do Saber. 1. ed. Porto Alegre: Penso, 1999.
Mais sobre Estatística e Epidemiologia
www.slides.com/lpmor22
laisepaixao@gmail.com
@lpmor22
Aulas Metodologia Científica
Contatos / Links