Candidate profile
Ludmila Augusta Soares Botelho
Departamento de Física - ICEx - Universidade Federal de Minas Gerais
AM
Who
I'm a Scientist!
I?
Martial Artist
Nerd
Woman
Brazilian
Physicist
Diverse
Femminist
Programmer
Gammer
I'm a Scientist!
AM
WHO
I?
Quantum Information Theory
Scientist
Physics
Programming
Mathematics
Writing
Teaching
Comunication
- MATLAB/Octave
- Mathematica
- Bash
- Python
- HTMLL + CSS
Programming
- MATLAB/Octave
- Mathematica
- Bash
- Python
- HTML + CSS

<div class="sl-block" data-block-type="text" style="height: auto; width: 441.792px; left: 38.208px; top: 71px;" data-name="text-c134d4" data-block-id="147ab4d1d9e31057ec30c3fa0d69c247">
<div class="sl-block-content" data-placeholder-tag="p" data-placeholder-text="Text" style="z-index: 16; color: rgb(0, 0, 0); font-size: 200%;">
<p>Programming</p>
</div>
</div>
<div class="sl-block" data-block-type="text" style="height: auto; width: 360.207px; left: 39.793px; top: 251px;" data-name="text-5e28fb" data-block-id="ca6502087f98061fa0c6477017a180b4" data-auto-animate-easing="cubic-bezier(0.755, 0.050, 0.855, 0.060)" data-auto-animate-delay="0.4">
<div class="sl-block-content" data-placeholder-tag="p" data-placeholder-text="Text" style="z-index: 17; color: rgb(34, 34, 34); font-size: 150%;">
<ul>
<li>MATLAB/Octave</li>
<li>Mathematica</li>
<li>Bash</li>
<li>Python</li>
<li>HTML + CSS</li>
</ul>
</div>
</div>


Experiment
Data

Quantum Mechanics


Data
Quantum State

Masters Thesis
2-1
$$\vert \alpha \rangle$$
signal
50/50
$$I_{21} = I_1 - I_2$$
Homodyne Tomography
Intensity \(\propto\) Photon number
Quadratures

Radon Transform
$$\langle{q_{\theta}}\vert\rho \vert{q_{\theta}}\rangle \rightarrow W(q,p)$$
$$W(q,p) \rightarrow \langle{q_{\theta}}\vert\rho \vert{q_{\theta}}\rangle $$
?
Inverse Radon
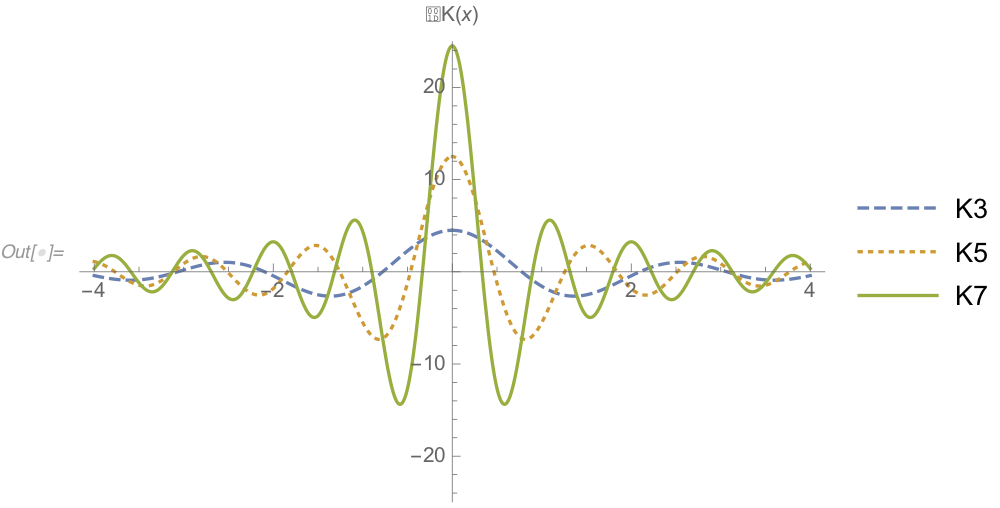

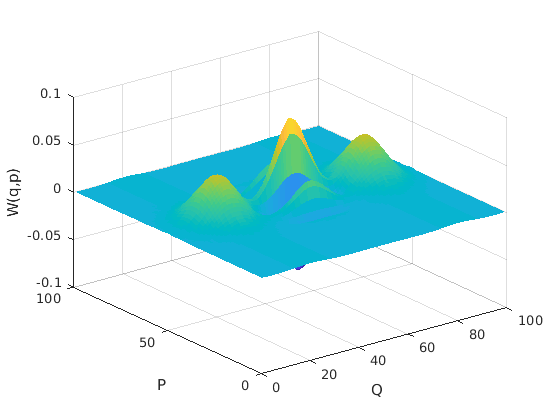


What about more general state?

Or Different types of measurements?
Convex Optmization
min
s.t
$$\rho \succeq 0$$
$$\mathrm{Tr}(\rho) = 1$$
-
Semi-definite programming
-
Fock Basis
$$\sum_{i \in \mathcal{I}} \Delta_i + \delta$$
$${\rho, \Delta, \delta}$$
$$\left\vert \mathrm{Tr}({E_i \rho) -f_i} \right\vert \leqslant \Delta_i f_i$$
$$i \in \mathcal{I}$$
$$\mathrm{Tr}({ E_i\rho} )\leqslant \delta$$
$$i \notin \mathcal{I}$$
$$\vert q_{\theta}\rangle\!\langle{q_{\theta}}\vert= \sum \psi_n^*(q) \psi_m(q) \exp[i(m-n)]\vert{n}\rangle\!\langle{m}\vert$$
Representations
Discrete

Continuous


Quantum States
Discrete
Continuous

Convex OPTIMIZATION
-
Semi-definite programming
-
Fock Basis

$$\vert q_{\theta}\rangle\!\langle{q_{\theta}}\vert= \sum \psi_n^*(q) \psi_m(q) \exp[i(m-n)]\vert{n}\rangle\!\langle{m}\vert$$
% cleaning yalmip memory
yalmip('clear');
F = class('double');
% defining the SDP variables
Rho = sdpvar(df,df,'hermitian','complex');
% standard constraints
F=[Rho>=0];
F=[F,trace(Rho)==1];
% observables
Obs=projX_LARGE;
Prob = (medidas+noise);
DELTA = sdpvar(length(projX_LARGE),length(projX_LARGE),'full','real');
F=[F,DELTA>=0];
delta = sdpvar(1,1,'full','real');
F=[F,delta>=0];
for i=1:length(projX_LARGE)
for j=1:length(projX_LARGE)
F=[F,trace(Rho*Obs{i,j})<=Prob(i,j)+DELTA(i,j)];
F=[F,trace(Rho*Obs{i,j})>=Prob(i,j)-DELTA(i,j)];
end
end
F=[F,trace(Rho*E_n)<=delta];
% cost function
E = sum(sum(DELTA))+delta;
ops = sdpsettings('solver','mosek','verbose',1);
ops.mosek.MSK_IPAR_NUM_THREADS=6;
SOLUTION=optimize(F,E,ops);
disp('DEBUGGING');
problema = double(SOLUTION.problem);
disp(yalmiperror(problema));
Rho = value(Rho);
DELTA = value(DELTA);
delta = value(delta);min
s.t
$$\rho \succeq 0$$
$$\mathrm{Tr}(\rho) = 1$$
$$\sum_{i \in \mathcal{I}} \Delta_i + \delta$$
$${\rho, \Delta, \delta}$$
$$\left\vert \mathrm{Tr}({E_i \rho) -f_i} \right\vert \leqslant \Delta_i f_i$$
$$i \in \mathcal{I}$$
$$\mathrm{Tr}({ E_i\rho} )\leqslant \delta$$
$$i \notin \mathcal{I}$$
arXiv:1911.09648v2 [quant-ph]
Add here:
Master's figures from thesis
Article figures






Positive Maps
- Density Operator -> Moment Matrix
- Entanglement Witness
(But Not Completely Positive)
Sep
$$\rho$$
$$\mathit{W}$$
Ent
$$M$$
$$\mathit{W}'$$



Did someone say "Applications"?






bosonic systems
bosonic systems
= continuous variables

innovation
relevant
urgent
a robust quantum computing infrastructure
vanguard
novelty
vanguard
innovation
novelty
vanguard
relevant
novelty
vanguard
relevant
urgent
novelty
vanguard
relevant
urgent
a robust quantum computing infrastructure
Good Quantum Softwares/Computers
... and computational science!
=
Deep knowledge about Quantum Physics
and communication theory, mathematics, etc.
I AM
What
looking for?

I AM
What
looking for?




Some business card?
