how to use hybrid quantum annealing algorithms to Solve Railway Dispatching Problems
Institute of Theoretical and Applied Informatics, Polish Academy of Sciences
Ludmila Botelho
Quantum computing devices
Noisy
Intermediate-
Scale
Quantum computing






Where is \(\omega\)?

N
Prime factors of
?
What can we do?
$$ H = - \sum_{i > j} J_{ij}Z_i Z_j - \sum _i h_iZ_i, $$
2-Local Ising model
- Quantum Annealing
Pauli \(Z\) Gates on \(i\)-th qubit
Ground state = optimal solution





- Initialize the annelear: \(|+^n\rangle\)
Ground state of:
$$ H_{QA}(t) = g(t/ \tau )H_{\text{mix}}+ h(t/ \tau)H$$
$$ H_{\text{mix}} = \sum_i X_i$$

What can we do?
Hybrid solution

Railway Dispatching Problem


Railway Dispatching Problem



Railway Dispatching Problem

-
integer linear program
QUBO
-
Minimizing quadratic functions
$$ y=x^TQx $$
-
Penalty Method
$$ \text{min } y=f(x) $$
$$ \text{subject to: } x_1 +x_2 + x_3= 1 $$
$$\text{min }y=f(x)+P\left(\sum_{i=1}^3 x_i -1\right)^2 $$
Binary variables
Constants
Results

First set of experiments
1. Double track line with dense traffic, random delays on departing
Results
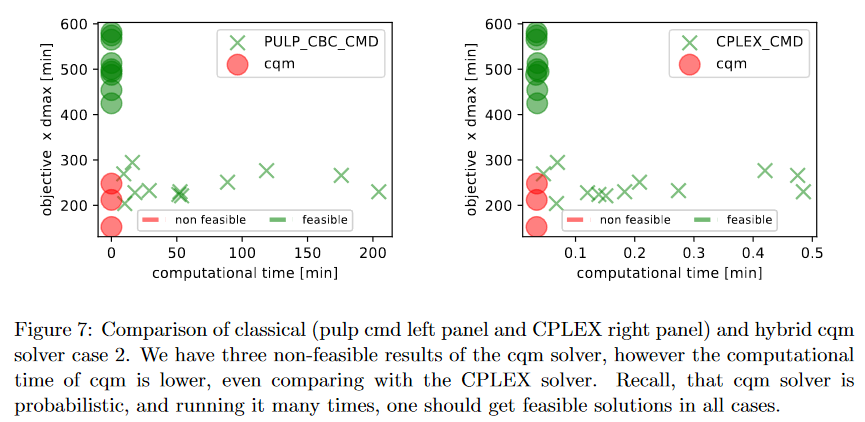
2. Similar to scenario 1 but one track is partially blocked
First set of experiments
Results
3. Simplified single track, few stations
First set of experiments

Results

Second set of experiments
Results
Second set of experiments


Results
Second set of experiments


Conclusion
- Constant computational time, regardless of the problem complexity
- ... But the experiment returned feasible solutions
- We have not reached the quantum computing supremacy...
Thank you!
Dziękuję!
Obrigada!
धन्यवाद!
Teşekkür ederim!
Köszönöm!
ধন্যবাদ !

And Now for Something Completely Different




