{add_to_codebook}
Ludmila Botelho
# THE CODEBOOK
Our Services
We offer a variety of services and plans tailored to business needs of any kind and of any size.
Process
Research
What does the user need to understand quantum computers? What is relevant?
1.
2.
Make a syllabus
What we expect from the module? Deliverables
- Exercises
- Code
3.
Build the page
Add the content to web-page: theory + coding challenges (codercises)
- Testing is important!
- Review
# ADDING NEW CONTENT
New Module!
Distance Measures
# DISTANCE MEASURES
(Taxicab metric)
(Euclidian distance)
# DISTANCE MEASURES
(Triangle inequality)
- \( d(p_1,p_1) = 0\)
- \( d(p_1,p_2) \geq 0\)
- \( d(p_1,p_2) = d(p_2,p_1)\)
- \( d(p_1,p_3) \leq d(p_1,p_2)+d(p_2,p_3)\)
(Symmetry)









(Symmetry)


(Isomorphism)



(Earth mover's distance)





(Hack week)



What about quantum states?



What about quantum states?




# A LIT BIT OF MATHEMATICS





?
?
?
?
# A LIT BIT OF MATHEMATICS




\(\frac{1}{4}\)
\(\frac{1}{4}\)
\(\frac{1}{4}\)
\(\frac{1}{4}\)
# A LIT BIT OF MATHEMATICS
Probabilities
# A LIT BIT OF MATHEMATICS
\(\frac{1}{4}\)
\(\frac{1}{4}\)
\(\frac{1}{4}\)
\(\frac{1}{4}\)




Probability vector
( \(\mathcal{l}_1\)-norm)
\(+\)
\(+\)
\(+\)
\(=\)
\(1\)
# A LIT BIT OF MATHEMATICS
$$\vert \psi \rangle = \begin{bmatrix} \alpha \\ \beta \end{bmatrix} $$
\(|\alpha|^2+|\beta|^2=1\)
(\(\mathcal{l}_2\)-norm)
\(\alpha,\beta\in \mathbb{C}\)

# A LIT BIT OF MATHEMATICS

$$ \rho = \rho^\dagger = \begin{bmatrix} a & c \\ b & d \end{bmatrix} $$
\(a + b =1\)
$$\rho = \begin{bmatrix} a & b \\ c & d \end{bmatrix} $$
$$ \langle \psi \vert \rho \vert \psi \rangle \geq 0$$
(Hermitian)
(Positive semi-definite)
\(a, b \in[0,1]\)
# A LIT BIT OF MATHEMATICS
\(a_1\)
\(a_2\)
\(a_3\)
\(\vdots\)
\(a_n\)
\(b_1\)
\(b_2\)
\(b_3\)
\(b_n\)
\(\vdots\)
\(|a_1 - b_1|\)
+
\(|a_2 - b_2|\)
+
\(|a_3 - b_3|\)
+
\(\vdots\)
+
\(|a_n-b_n|\)
$$\rho = \begin{bmatrix} a_{11} & \ldots & a_{1n} \\ \vdots & \ddots & \vdots\\ a_{1n} & \ldots & a_{nn} \end{bmatrix} = VDV^\dagger$$
$$D= \begin{bmatrix} d_{1} & & \\ & \ddots & \\ & & d_{n} \end{bmatrix}$$
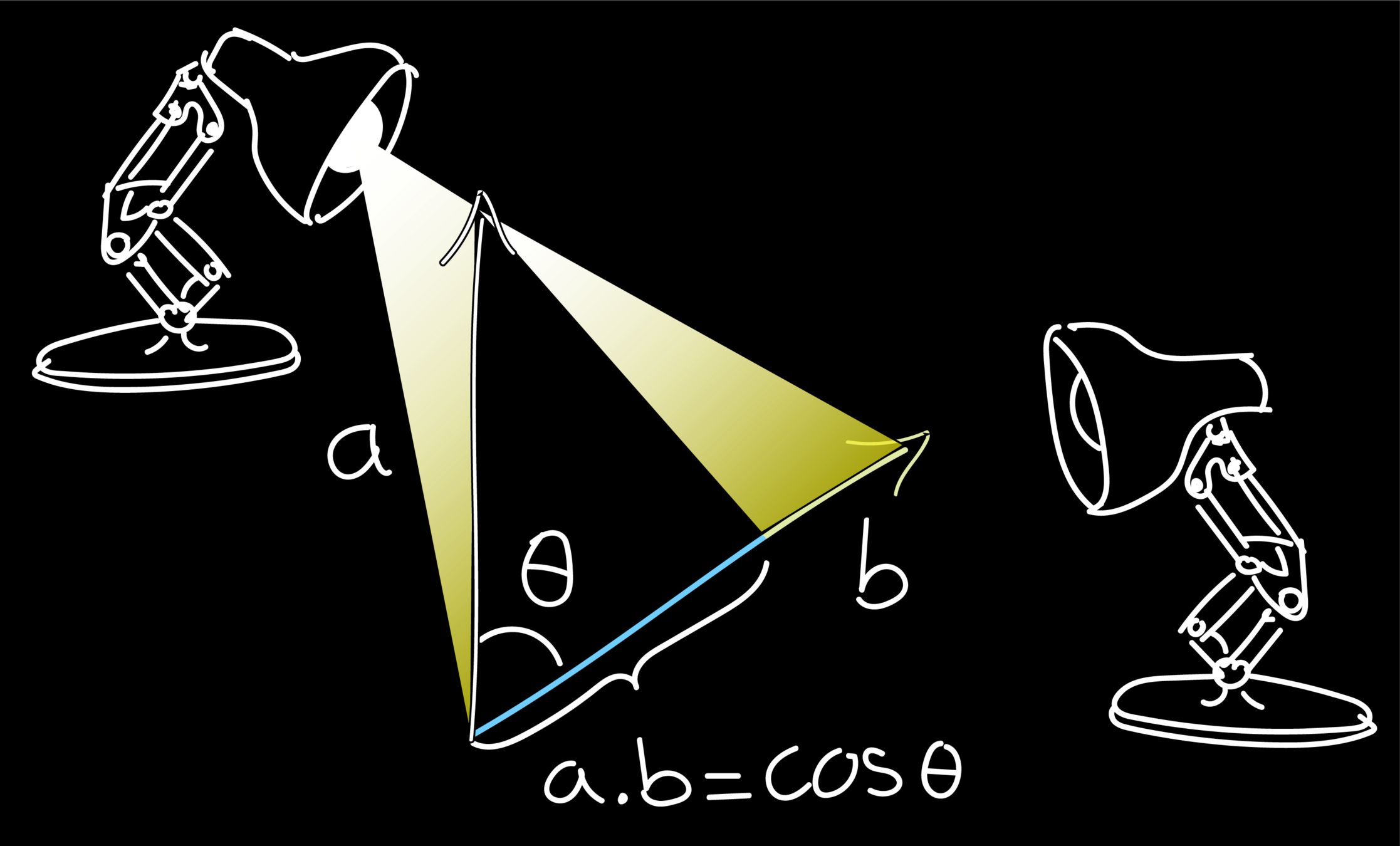
Distance between vectors
# A LIT BIT OF MATHEMATICS
\(a_1\)
\(a_2\)
\(a_3\)
\(\vdots\)
\(a_n\)
\(b_1\)
\(b_2\)
\(b_3\)
\(b_n\)
\(\vdots\)
# A LIT BIT OF MATHEMATICS
\(a_1\)
\(a_2\)
\(a_3\)
\(\vdots\)
\(a_n\)
\(b_1\)
\(b_2\)
\(b_3\)
\(b_n\)
\(\vdots\)

Fidelity (or Bhattacharyya Coefficient)
# LEARNING BY DOING IT

Exercises
# LEARNING BY DOING IT
Exercises

def kolmogorov_distance(p, q):
"""Compute the Kolmogorov distance between two discrete probability distributions.
Args:
p (np.array[float]): A vector of probability distribution
q (np.array[float]): A vector of probability distribution.
Returns:
(float): A number that represents the trace distance
of the probability distributions.
"""
##################
# YOUR CODE HERE #
##################
# CREATE A VECTOR x BASED ON p - q
# RETURN THE L1-NORM OF x DIVIDED BY 2
return Codercises
# LEARNING BY DOING IT
def kolmogorov_distance(p, q):
"""Compute the Kolmogorov distance between two discrete probability distributions.
Args:
p (np.array[float]): A vector of probability distribution
q (np.array[float]): A vector of probability distribution.
Returns:
(float): A number that represents the trace distance
of the probability distributions.
"""
##################
# YOUR CODE HERE #
##################
# CREATE A VECTOR x BASED ON p - q
x = p-q
# RETURN THE L1-NORM OF x DIVIDED BY 2
return np.sum(np.abs(x))/2# LEARNING BY DOING IT
Codercises
D.1
Metrics and Norms in vector space
Kolmogorov distance
D.2
Alternative measurement; Bhattacharyya coefficient
D.3
Metrics and norms for quantum operators
Trace distance
D.4
Fidelity

(Classical)

(Quantum)


D.1
Metrics and norms in vector space
Kolmogorov distance
D.2
Alternative measurement: Bhattacharyya coefficient
D.3
Metrics and norms for quantum operators
Trace distance
N.3
Partial trace and purification
User Questions
Error correction module review
Teleportation Demo review
N.4
The Bloch ball
Compute expectation value
D.4
Fidelity
