Examen Final Estadística Computacional

Luis Manuel Román García

Contenido

  • Inferencia Gráfica
  • Inferencia Gráfica (continua)
  • Bootstrap e Inferencia Bayesiana
  • MCMC
  • Convergencia
  • Modelos Jerárquicos

Inferencia Gráfica

Primera parte

El precio de una casa se ve directamente afectado por la demanda, si la demanda es baja el precio tenderá a ser bajo. Por ende se esperaría que casas con climas desfavorables tengan menor demanda y en consecuencia menor precio. Como hipótesis nula supondremos una relación lineal entre ambas variables.

Para probar nuestra hipótesis con una significancia del 5%, graficaremos los verdaderos valores contra 19 gráficas generadas siguiendo una relación lineal entre las variables .

Inferencia Gráfica

Primera parte

# Librerias
library( nullabor )
library( dplyr )
library( plyr )
library( ggplot2 )

# Lectura de datos.
data       <- read.table( "./data/places.csv",
				  stringsAsFactors = FALSE )

# Selección de variables.
data.graph <- select( data, 1:2 )

# Elaboración de prueba.
set.seed( 123454321 )
graph.null <- lineup( null_lm( HousingCost  ~ Climate  ),
		      data.graph, n = 20  )
# Gráfica
ggplot( graph.null, aes( x = Climate, y = HousingCost ) ) +
geom_point( alpha = .7, size = 2, color = "#1A237E" ) +
facet_wrap( ~ .sample, nrow = 2) + 
theme( text = element_text( color = "#E91E63",
			    face  = "bold" ),
       panel.background = element_blank( ) )

Inferencia Gráfica

Primera parte

Código

Inferencia Gráfica

Primera parte

Los datos pueden ser fácilmente detectados en la posición 10. Por lo tanto rechazamos la hipótesis nula.

> decrypt("ytIA Hiqi Un 0pTUqUpn bP")
[1] "True data in position 10"

Inferencia Gráfica

Primera parte

Conclusión

Primero leemos y procesamos los datos.

Inferencia Gráfica 

# Lectura y preparación de datos.
set.seed( 123454321 )
data <- read.csv("./data/wages.csv")%>%
		filter( hgc %in% c( 9, 10, 11 ) &
		        lnw <= 3.5 ) %>%
		mutate(race = ifelse( hispanic == 1, 
								 "hispanic", 
					             ifelse( black == 1, 
					             	     "black",
					             	      "white" ) ) ) %>%
		filter( id %in% unique( id[ race == "hispanic" ] ) |
				id %in% sample( unique( id[ race == "black" ] ),
								length( unique( id[ race == "hispanic" ] ) ) ) | 
				id %in% sample( unique( id[ race == "white" ] ),
								length( unique( id[ race == "hispanic" ] ) ) ) )

Segunda Parte

Para generar la hipótesis nula permutamos la raza.

set.seed( 123454321 )
data_null <- lineup( null_permute('race'), 
					 n = 20, data)

Inferencia Gráfica 

Segunda Parte

# Gráfico
ggplot( data_null, aes( x = exper, y = lnw ) ) +
geom_point( alpha = 0.25, size = 2, color = "#9E9E9E" ) + 
geom_smooth( aes( group = race, color = race ),
  			 method = "loess", se = FALSE ) +
facet_wrap( ~.sample ) + 
theme( text = element_text( color = "#E91E63",
							face  = "bold" ),
	   panel.background = element_blank( ) ) +
scale_color_manual( values = c( "#1A237E",
			        "#1565C0",
			        "#D500F9" ) )

Inferencia Gráfica 

Segunda Parte

Código

Inferencia Gráfica 

Segunda Parte

Gráfica

De tres individuos entrevistados, dos detectaron la gráfica con los valores  reales.

> decrypt("ytIA Hiqi Un 0pTUqUpn ba")
[1] "True data in position 16"

Bajo la hipótesis nula, cada ensayo es independiente y se distribuye Bernoulli con           . Con los tres ensayos tenemos una Binomial(3, .05). Luego entonces la probabilidad de observar nuestra muestra es de:

\theta = .05
θ=.05
P(x = 2| H_0) =P(x = 2| n = 3, \theta = .05) = \frac{3!}{2!1!}.05^2.95^1=0.007125 = p-value
P(x=2∣H​0​​)=P(x=2∣n=3,θ=.05)=​2!1!​​3!​​.05​2​​.95​1​​=0.007125=p−value

Inferencia Gráfica 

Segunda Parte

Se rechaza la hipótesis nula de que la raza no tiene un efecto sobre el salario de los individuos con nivel escolar 9, 10, 11 con una significancia de 0.007125

Inferencia Gráfica 

Segunda Parte

Conclusión

Bootstrap Paramétrico

Bootstrap e Inferencia Bayesiana

x_1, x_2, ..., x_n.\quad iid\quad N(0,\sigma^2)
x​1​​,x​2​​,...,x​n​​.iidN(0,σ​2​​)

Supongamos que tenemos 

y queremos encontrar un estimador de máxima verosimilitud para    . Para lograr esto calculamos la log-verosimilitud                                                    e igualamos a cero para obtener:                  que en este caso se reduce a:

\sigma^2
σ​2​​
log(f_x(x)) = log(\displaystyle\prod_{i = 1}^nf_{x_i}(x_i)) = -\frac{n}{2}log(2\pi\sigma^2)-\displaystyle\sum_{i = 1}^n\frac{(x-\mu)^2}{2\sigma^2}
log(f​x​​(x))=log(​i=1​∏​n​​f​x​i​​​​(x​i​​))=−​2​​n​​log(2πσ​2​​)−​i=1​∑​n​​​2σ​2​​​​(x−μ)​2​​​​
\hat{\sigma^2}=\frac{1}{n}\displaystyle\sum_{i=1}^n(x-\mu)^2
​σ​2​​​^​​=​n​​1​​​i=1​∑​n​​(x−μ)​2​​
\hat{\sigma^2} = \frac{1}{n}\displaystyle\sum_{i = 1}^nx^2
​σ​2​​​^​​=​n​​1​​​i=1​∑​n​​x​2​​

Bootstrap Paramétrico

Bootstrap e Inferencia Bayesiana

Con los datos que tenemos en este ejemplo

##############
##Pregunta 2##
##############

# Lectura de datos.
load("./data/x.RData")

# Función máx verosimilitud
var.hat <- function( x ){
	sum( ( x - mean( x ) )^2 ) / length( x )
}

> var.hat(x)
[1] 130.9725
\hat{\sigma^2}=130.9725
​σ​2​​​^​​=130.9725

Bootstrap Paramétrico

Bootstrap e Inferencia Bayesiana

# Realización bootstrap del estimador de mv de 
# sigma^2
boot.var <- function( x ){
	x <- sample( x, length( x ), TRUE )
	var.hat( x )
}

# N realizaciones bootstrap del estimador de 
# mv de sigma^2
n.boot.var <- function( x, n = 1000 ){
	replicate( n, boot.var( x ) )
}

set.seed(123454321)

data <- data.frame( x = n.boot.var( x ) )
ggplot(data = data,
	   aes(x = x ) ) +
geom_histogram( alpha = .5, fill = "#1A237E",
	            col = "#E91E63" ) + 
theme( text = element_text( color = "#E91E63",
							face  = "bold" ),
	   panel.background = element_blank( ) )

# Error estandar
s.e <- sqrt(sum( ( data$x - mean( data$x ) )^2 ) / nrow( data ) )

Para estimar el error estandar corremos el siguiente código

se = 14.04

Análisis Bayesiano

Bootstrap e Inferencia Bayesiana

Ahora supongamos que  

\sigma2
σ2

sigue una distribución a priori

Gamma inversa:

f(x)=\frac{\beta^{\alpha}}{\Gamma(\alpha)}x^{-1-\alpha}e^{-\frac{\beta}{x}}
f(x)=​Γ(α)​​β​α​​​​x​−1−α​​e​−​x​​β​​​​

Análisis Bayesiano

Bootstrap e Inferencia Bayesiana

Dado que no tenemos mucha información sobre la muestra ni el fenómeno que estas variables describen, lo más razonable es suponer una distribución a priori no muy informativa, o en otras palabras que no sea muy picuda.

\alpha = 10,\quad \beta = 100
α=10,β=100

Parece ser una opción razonable pues no acumula demasiada probabilidad en ningún intervalo.

Análisis Bayesiano

Bootstrap e Inferencia Bayesiana

\alpha = 10,\quad \beta = 100
α=10,β=100

Análisis Bayesiano

Bootstrap e Inferencia Bayesiana

Para calcular anlíticamente la distribución posterior, necesitamos de la distribución a priori y de la verosimilitud.

P(\theta|x)=\frac{p(x|\theta)p(\theta)}{p(x)}
P(θ∣x)=​p(x)​​p(x∣θ)p(θ)​​

Análisis Bayesiano

Bootstrap e Inferencia Bayesiana

Para calcular anlíticamente la distribución posterior, necesitamos de la distribución a priori y de la verosimilitud.

P(\theta|x)=\frac{p(x|\theta)p(\theta)}{p(x)}
P(θ∣x)=​p(x)​​p(x∣θ)p(θ)​​
p(x|\theta)p(\theta) =
p(x∣θ)p(θ)=
(\frac{1}{(2\pi\sigma^2)^{-\frac{n}{2}}}e^{\displaystyle\sum_{i=1}^n\frac{(x_i-\mu)^2}{2\sigma^2}})(\frac{\beta^{\alpha}}{\Gamma(\alpha)}{\sigma^2}^{(-1-\alpha)}e^{-\frac{\beta}{\sigma^2}})
(​(2πσ​2​​)​−​2​​n​​​​​​1​​e​​i=1​∑​n​​​2σ​2​​​​(x​i​​−μ)​2​​​​​​)(​Γ(α)​​β​α​​​​σ​2​​​(−1−α)​​e​−​σ​2​​​​β​​​​)
{\sigma^2}^{(-(\alpha + \frac{n}{2})-1)}e^{\displaystyle\sum_{i=1}^n\frac{(x_i-\mu)^2}{2\sigma^2}-\frac{\beta}{\sigma^2}}
σ​2​​​(−(α+​2​​n​​)−1)​​e​​i=1​∑​n​​​2σ​2​​​​(x​i​​−μ)​2​​​​−​σ​2​​​​β​​​​
= \frac{\beta^{\alpha}{\sigma^2}^{(-1-\alpha)}}{\Gamma(\alpha)(2\pi\sigma^2)^{-\frac{n}{2}}}e^{\displaystyle\sum_{i=1}^n\frac{(x_i-\mu)^2}{2\sigma^2}-\frac{\beta}{\sigma^2}}
=​Γ(α)(2πσ​2​​)​−​2​​n​​​​​​β​α​​σ​2​​​(−1−α)​​​​e​​i=1​∑​n​​​2σ​2​​​​(x​i​​−μ)​2​​​​−​σ​2​​​​β​​​​

Análisis Bayesiano

Bootstrap e Inferencia Bayesiana

Supongamos ahora que el parámetro que deseamos estimar es                 . Como los estimadores de máxima verosimilitud son equivariantes bajo transformaciones 1 a 1 tenemos que: 

\tau = log(\sigma)
τ=log(σ)
\hat{\tau}_{MV} = log(\sqrt{\hat{\sigma}^2_{MV}})
​τ​^​​​MV​​=log(√​​σ​^​​​MV​2​​​​​)

Bootstrap Paramétrico

Bootstrap e Inferencia Bayesiana

Estimando con bootstrap paramétrico, obtenemos.

# Función máx verosimilitud
tau.hat <- function( x ){
	log( sqrt( sum( ( x - mean( x ) )^2 ) / length( x ) ) )
}

# Realización bootstrap del estimador de mv de 
# sigma^2
boot.var <- function( x ){
	x <- sample( x, length( x ), TRUE )
	tau.hat( x )
}

# N realizaciones bootstrap del estimador de 
# mv de sigma^2
n.boot.var <- function( x, n = 1000 ){
	replicate( n, boot.var( x ) )
}

set.seed( 123454321 )
data <- data.frame( x = n.boot.var( x ) )
ggplot(data = data,
	   aes(x = x ) ) +
geom_histogram( alpha = .5, fill = "#1A237E") + 
theme( text = element_text( color = "#E91E63",
							face  = "bold" ),
	   panel.background = element_blank( ) )

s.e <- sqrt(sum( ( data$x - 
				   mean( data$x ) )^2 ) /
	   nrow( data ) )
CI_{95\%} = [2.323498,2.541974]
CI​95%​​=[2.323498,2.541974]

Análisis Bayesiano

Bootstrap e Inferencia Bayesiana

Estimando con una distribución a priori 

# Bayesiana
set.seed( 123454321 )
log.sigma <- c()
for(i in 1:1000){
u   <- runif( 1000, .1, 300 ) 
log.sigma[i] <- log( sqrt( u )  )
}
ggplot(data = data.frame(x = log.sigma),
	   aes(x = x ) ) +
geom_histogram( alpha = .5, fill = "#1A237E") + 
theme( text = element_text( color = "#E91E63",
							face  = "bold" ),
	   panel.background = element_blank( ) )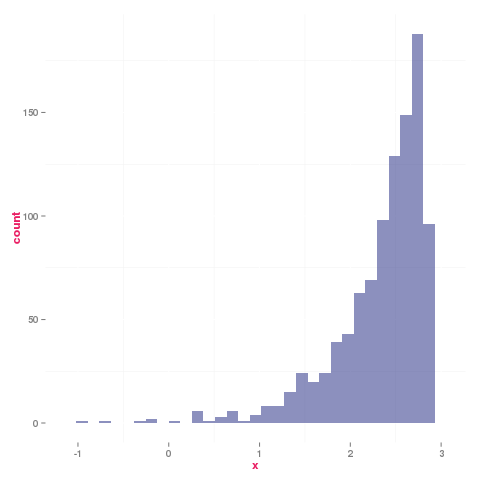
U(a = .1, b = 300)
U(a=.1,b=300)

Caminata aleatoria

MCMC

En esta primera sección, llevaremos a cabo 6,000 pasos de un modelo MCMC con brincos normales. Llevaremos a cabo el experimento con tres valores distintos de 

N(0, 5),\quad N(0,.2),\quad N(0, 20)
N(0,5),N(0,.2),N(0,20)
\sigma^2
σ​2​​

Caminata aleatoria

MCMC

Para esta sección utilizamos el siguiente código: 

prior <- function(mu = 100, tau = 10){
  function(theta){
    dnorm(theta, mu, tau)
  }
}
mu <- 150
tau <- 15
mi_prior <- prior(mu, tau)
S <- 13000
S2 <- 1700000
N <- 100
#sigma2 <- S2 / N - (S / N) ^ 2
sigma <- 20
  
likeNorm <- function(S, S2, N, sigma = 20){
  sigma2 = sigma ^ 2
  function(theta){
    1 / (2 * pi * sigma2) * exp(-1 / (2 * sigma2) * (S2 - 2 * theta * S + 
        N * theta ^ 2))
  }
}

mi_like <- likeNorm(S = S, S2 = S2, N = N, sigma = sigma)
postRelProb <- function(theta){
  mi_like(theta) * mi_prior(theta)
}
# para cada paso decidimos el movimiento de acuerdo a la siguiente función
caminaAleat <- function(theta, sd_prop = 5){ # theta: valor actual
  salto_prop <- rnorm(n = 1, sd = sd_prop) # salto propuesto
  theta_prop <- theta + salto_prop # theta propuesta
  u <- runif(1) 
  p_move = min(postRelProb(theta_prop) / postRelProb(theta), 1) # prob mover
  if(p_move  > u){
    return(theta_prop) # aceptar valor propuesto
  }
  else{
    return(theta) # rechazar
  }
}


pasos <- 6000
camino1 <- numeric(pasos) # vector que guardará las simulaciones
camino2 <- numeric(pasos) # vector que guardará las simulaciones
camino3 <- numeric(pasos) # vector que guardará las simulaciones

camino1[1] <- 90 # valor inicial
camino2[1] <- 90 # valor inicial
camino3[1] <- 90 # valor inicial


rechazo1 = 0
rechazo2 = 0
rechazo3 = 0

# Generamos la caminata aleatoria
for (j in 2:pasos){
  camino1[j] <- caminaAleat(camino1[j - 1])
  camino2[j] <- caminaAleat(camino2[j - 1], .2 )
  camino3[j] <- caminaAleat(camino3[j - 1], 20 )

  rechazo1 <- rechazo1 + 1 * (camino1[j] == camino1[j - 1]) 
  rechazo2 <- rechazo2 + 1 * (camino2[j] == camino2[j - 1]) 
  rechazo3 <- rechazo3 + 1 * (camino3[j] == camino3[j - 1]) 

}
rechazo1 / pasos
rechazo2 / pasos
rechazo3 / pasos

Caminata aleatoria

MCMC

Y para las gráficas 

ggplot( data = data.frame( x = 1:2000,
						   camino1 = camino1[ 1:2e3 ],
						   camino2 = camino2[ 1:2e3 ],
						   camino3 = camino3[ 1:2e3 ] ),
		aes(x = x, y = camino1 ) ) + 
#geom_point(col = "#E91E63" ) + 
geom_line( aes( x = x, y = camino1 ), col = "#1A237E" ) + 
##geom_point( aes( x = x, y = camino2 ), col = "#E91E63" ) + 
geom_line( aes( x = x, y = camino2 ), col = "#1565C0" ) + 
##geom_point( aes( x = x, y = camino3 ), col = "#E91E63" ) + 
geom_line( aes( x = x, y = camino3 ), col = "#D500F9" )  + theme( text = element_text( color = "#E91E63",
							face  = "bold" ),
	   panel.background = element_blank( ) ) + ylab("") +
xlab("Pasos")

Caminata aleatoria

MCMC

Es claro que entre menor es la desviación estandar, el conjunto propuesto es más estrecho y por ende le toma más tiempo recorrer una muestra que represente a la distribución.

Caminata aleatoria

MCMC

Para la tasa de rechazo simplemente ejecutamos el siguiente código:

> rechazo1 / pasos
[1] 0.5705
> rechazo2 / pasos
[1] 0.05533333
> rechazo3 / pasos
[1] 0.8751667
>
\%M_{N(0,.2)} = .05
%M​N(0,.2)​​=.05
\% M_{N(0,5)} = .57
%M​N(0,5)​​=.57
\% M_{N(0,20)} = .87
%M​N(0,20)​​=.87

Caminata aleatoria

MCMC

Histogramas

M_{N(0,5)}
M​N(0,5)​​
M_{N(0,.2)}
M​N(0,.2)​​
M_{N(0,20)}
M​N(0,20)​​
# histogramas
ggplot(data = data.frame( x = 1:4001,
						   camino1 = camino1[ 2e3:6e3 ],
						   camino2 = camino2[ 2e3:6e3 ],
						   camino3 = camino3[ 2e3:6e3 ] ),
		aes(x = camino1 )) +
  geom_histogram(aes(y = ..density..), fill ="#1A237E", alpha = .7) +
   theme( text = element_text( color = "#E91E63",
							face  = "bold" ),
	   panel.background = element_blank( ) )
  
ggplot(data = data.frame( x = 1:4001,
						   camino1 = camino1[ 2e3:6e3 ],
						   camino2 = camino2[ 2e3:6e3 ],
						   camino3 = camino3[ 2e3:6e3 ] ),
		aes(x = camino2 )) +
  geom_histogram(aes(y = ..density..), fill ="#1565C0", alpha = .7) +
   theme( text = element_text( color = "#E91E63",
							face  = "bold" ),
	   panel.background = element_blank( ) )

ggplot(data = data.frame( x = 1:4001,
						   camino1 = camino1[ 2e3:6e3 ],
						   camino2 = camino2[ 2e3:6e3 ],
						   camino3 = camino3[ 2e3:6e3 ] ),
		aes(x = camino3 )) +
  geom_histogram(aes(y = ..density..), fill ="#D500F9", alpha = .7) +
   theme( text = element_text( color = "#E91E63",
							face  = "bold" ),
	   panel.background = element_blank( ) )

Caminata aleatoria

MCMC

Histogramas

Es interesante notar que  el modelo que usa            no alcanza a muestrear adecuadamente la distribución (esto se debe a que la distribución propuesta es muy estrecha). Mientras que el modelo con            muestra ciertas irregularidades (esto se debe a la alta tasa de rechazo). Por otro lado, la elección de          parece balancear bien ambos efectos pues nos da larepresentación más cercana a la verdadera distribución posterior.

\sigma = .02
σ=.02
\sigma = 20
σ=20
\sigma = 5
σ=5

Caminata aleatoria

MCMC

Predictiva Posterio

p(y)=\int p(y|\theta)p(\theta|x)d\theta
p(y)=∫p(y∣θ)p(θ∣x)dθ

Recordando que                                  podemos generar un histograma y un intervalo de 95% de confianza para la distribución de predicción. Cómo vimos, el modelo que mejor reproduce la distribución posterior es el que usa         por lo que es el que usaremos.

\sigma = 5
σ=5
#Distribución de predicción
camino1 <- camino1[ 2e3:6e3 ]
y_sims <- rnorm(1:length(camino1), mean(camino1), sd(camino1))

ggplot(data = data.frame(x = y_sims), aes(x = x)) + 
  geom_histogram(fill = "#D500F9") +
  geom_vline(aes(xintercept = mean(y_sims)), color = "#1565C0") +
   theme( text = element_text( color = "#E91E63",
							face  = "bold" ),
	   panel.background = element_blank( ) )
# banda de confianza.
   set.seed( 123454321 )
   mean.y <- c()
   sd.y   <- c()
   for(i in 1:1000){
   		samp.y      <- sample( y_sims, length( y_sims ), TRUE )
   		mean.y[ i ] <- mean( samp.y )
   		sd.y[ i ]   <- sd( samp.y )
	}
	samp.y <- sample(y_sims,1000, TRUE)
 ggplot(data = data.frame( x   = 1:1000, 
 						   y   = samp.y, 
 						   up  = mean.y + 2*sd.y,
 						   low = mean.y - 2*sd.y ),
 aes(x = x, y = y) ) + geom_point( col = "#E91E63" ) +
 geom_segment( aes(x = x, xend = x, y = up, yend = low),
 alpha = .3, col =  "#1565C0" ) + ylim(120, 140)+
   theme( text = element_text( color = "#E91E63",
							face  = "bold" ),
	   panel.background = element_blank( ) )

134.2846

126.4218

Estimación de Coeficientes

Convergencia

En esta sección buscamos estimar los valores de los coeficientes de un modelo de regresión lineal. En particular estamos suponiendo la siguientes distribuciones iniciales:

y_i \quad N(\alpha + \beta x_i, \sigma^2)
y​i​​N(α+βx​i​​,σ​2​​)

con

\beta\quad N(0, 1000)
βN(0,1000)
\sigma^2\quad U(0,1000)
σ​2​​U(0,1000)

Estimación de Coeficientes

Convergencia

Para esto utilizamos muestreo de Gibbs, es necesario determinar cuantas iteraciones se deben hacer así como también cuantas realizaciones se deben eliminar por pertencer al periodo de calentamiento.

Estimación de Coeficientes

Convergencia

La métodología que seguiré es la siguiente:

Primer realización

  • 10 cadenas
  • 1000 iteraciones
  • 0  entrenamiento

El hecho de que sean 10 cadenas robustecerá los resultados pues nos ayuda a identificar si en verdad se converge a un modelo en común. 1000 iteraciones para garantizar convergencia (en caso de que la haya, de lo contrario aumentar número de iteraciones en la siguiente realización). 0 muestras en el entrenamiento para determinar a partir de que iteración los estimadores se estabilizan.

Estimación de Coeficientes

Convergencia

                         mu.vect    sd.vect        2.5%           25%                 50%                    75%                97.5%      Rhat       n.eff
a                            1.327      0.029       1.270           1.307             1.327                  1.348                 1.385      1.001        10000
b                           -0.614      0.073      -0.758         -0.663            -0.614                 -0.565                -0.474      1.001        6400
sigma.y                0.823      0.019        0.787           0.811             0.823                  0.836                 0.862      1.001        5800
deviance        2250.000     2.426      2247.235      2248.222       2249.369         2251.086       2256.276     1.001        5900

Vemos que la devianza es bastante grande, esto puede deberse a la variabilidad que introducen los primeros valores, esto nos indica que es correcto quemar las primeras iteraciones. De igual forma

los valores se estabilizan rápidamente, esto es señal de que podemos disminuir el número de iteraciones.

pD = 2.9 and DIC = 2252.9

Estimación de Coeficientes

Convergencia

Segunda realización

  • 10 cadenas
  • 50 iteraciones
  • 20  entrenamiento

Mantuvimos las 10 cadenas para robustecer los resultados, redujimos significativamente el número de iteraciones pues el modelo converge rápidamente, eliminamos los primeros 20 valores pues la devianza era muy alta.

Estimación de Coeficientes

Convergencia

                         mu.vect    sd.vect        2.5%           25%                 50%                    75%                97.5%      Rhat       n.eff
a                            1.329      0.030        1.275          1.308              1.330                   1.351                1.388       1.003        300
b                           -0.620      0.070       -0.753         -0.663            -0.625                  -0.572              -0.477        0.999       300
sigma.y               0.823       0.020         0.784          0.809              0.822                   0.836              0.863        1.000        300
deviance       2250.043      2.324      2247.230    2248.116     2249.540              2251.237        2255.937    1.029      140

Disminuyo la devianza, los estimadores siguieron convergiendo y redujimos significativamente el 

número de iteraciones, de igual forma redujimos el pD y DIC por lo que estos parámetros son mucho mejores que los iniciales.

pD = 2.6 and DIC = 2252.7

Estimación de Coeficientes

Convergencia

Gráficas

Se puede ver que todas las cadenas convergen aproxiamdamente al mismo modelo.

Caminata aleatoria

Modelos Jerárquicos

En este problema veremos como asignar incertidumbre a la distribución a priori de los parámetros por medio de un modelo jerárquico. 

Caminata aleatoria

Modelos Jerárquicos

Si hacemos un simil entre los conejos del experimento y un lanzamiento de volados podemos ver que:

  • Un conejo desarrollará un tumor con probabilidad     . Esto que puede ser visto como la probabilidad de éxito en un volado. Los conejos representan monedas.
  • Los experimentos representan volados. Mi incertidumbre sobre que impacto puede tener el tratamiento sobre los conejos se representa con el hiperparámetro       .
\theta
θ
\mu
μ

Caminata aleatoria

Modelos Jerárquicos

Si hacemos un simil entre los conejos del experimento y un lanzamiento de volados podemos ver que:

  • Un conejo desarrollará un tumor con probabilidad     . Esto que puede ser visto como la probabilidad de éxito en un volado. Los conejos representan monedas.
  • Los experimentos representan volados. Mi incertidumbre sobre que impacto puede tener el tratamiento sobre los conejos se representa con el hiperparámetro       .
\theta
θ
\mu
μ

Caminata aleatoria

Modelos Jerárquicos

Estimaremos la distribución posterior de los parámetros con un muestreador de Gibbs.

\theta
θ
\mu
μ
K
K
Beta(a,b),\quad a = \mu k, \quad b = (1-\mu)k
Beta(a,b),a=μk,b=(1−μ)k
Beta(A_\mu,B_\mu)
Beta(A​μ​​,B​μ​​)
Gamma(S_k, R_k)
Gamma(S​k​​,R​k​​)
#Modelo Jerarquico
load("data/rabbits.RData")
modelo_rabbit.txt <-
'
model{
  for(t in 1:N){
    x[t] ~ dbern(theta[coin[t]])
  }
  for(j in 1:nCoins){
    theta[j] ~ dbeta(a, b)
  }
  a <- mu * kappa
  b <- (1 - mu) * kappa
  # A_mu = 2, B_mu = 2
  mu ~ dbeta(1, 1)
  kappa ~ dgamma(1, 0.1)
}
'


cat(modelo_rabbit.txt, file = 'modelo_rabbit.bugs')

x <- rabbits$tumor
coin <- rabbits$experiment

jags.inits <- function(){
  list("mu" = runif(1, 0.1, 0.9),
    "kappa" = runif(1, 5, 20))
}

jags_fit <- jags(
  model.file = "modelo_rabbit.bugs",    # modelo de JAGS
  inits = jags.inits,   # valores iniciales
  data = list(x = x, coin = coin, nCoins = length(coin),  N = length(x)),    # lista con los datos
  parameters.to.save = c("mu", "kappa", "theta"),  # parámetros por guardar
  n.chains = 3,   # número de cadenas
  n.iter = 10000,    # número de pasos
  n.burnin = 1000   # calentamiento de la cadena
  )
sims_df <- data.frame(n_sim = 1:jags_fit$BUGSoutput$n.sims,
                      jags_fit$BUGSoutput$sims.matrix) %>% 
  dplyr::select(-deviance) %>%
  gather(parametro, value, -n_sim)

Caminata aleatoria

Modelos Jerárquicos

Gráficas

\mu
μ
K
K
ggplot(filter(sims_df, parametro == "kappa"), aes(x = value)) +
  geom_histogram(alpha = 0.8, fill = "#1565C0") +
     theme( text = element_text( color = "#E91E63",
							face  = "bold" ),
	   panel.background = element_blank( ) )

ggplot(filter(sims_df, parametro == "mu"), aes(x = value)) +
  geom_histogram(alpha = 0.8, fill = "#1A237E") +
     theme( text = element_text( color = "#E91E63",
							face  = "bold" ),
	   panel.background = element_blank( ) )

    adquiere la forma de una distribución normal mientras que K se inclina de manera importante por valores cercanos a cero.

\mu
μ

Caminata aleatoria

Modelos Jerárquicos

Gráficas

	ggplot(filter(sims_df, ! parametro %in% c("mu", "kappa" ) ),
	aes(x = parametro, y = value ) ) + geom_boxplot( color = "#1A237E", 
	fill = "#1565C0") +
     theme( text = element_text( color = "#E91E63",
							face  = "bold" ),
	   panel.background = element_blank( ) )

Vemos que para  prácticamente todas las estimaciones de  se mantiene aproximadamente la misma distribución, sin embargo el número de outliers es importante.

\theta
θ

Caminata aleatoria

Modelos Jerárquicos

Gráficas

# Comparación medias
library(dat.table)
thetas  <- data.table(filter(sims_df, ! parametro %in% c("mu","kappa")))
thetas1 <- data.table(filter(sims_df1, ! parametro %in% c("mu","kappa")))
setkey(thetas, parametro)
setkey(thetas1, parametro)
m.thetas <- thetas[ , mean(value), by = parametro]
m.thetas1 <- thetas1[ , mean(value), by = parametro]
m.thetas.t <- merge(m.thetas1,m.thetas, by = "parametro")
names(m.thetas.t) <- c("parametro", "model1", "model2")

ggplot(m.thetas.t, aes(x = model1, y = model2)) + geom_point(color = "#1565C0")+
     theme( text = element_text( color = "#E91E63",
							face  = "bold" ),
	   panel.background = element_blank( ) )

La relación es prácticamente lineal, aunque las medias del segundo modelo alcanzan valores más elveados que en el primero. Esto se debe a la diferencia en la distribución de la K. 

FIN

Made with Slides.com