Introduction to Deep Learning
Contents
- Neural network's architecture overview
- Activation functions
- Backpropagation
Neural network's architecture overview
Architecture overview
The most basic component of an artificial neural network is the activation unit.
It is made of an input, or set of n inputs (which may include a constant bias term) an 'activation' function and an output.
Activation node
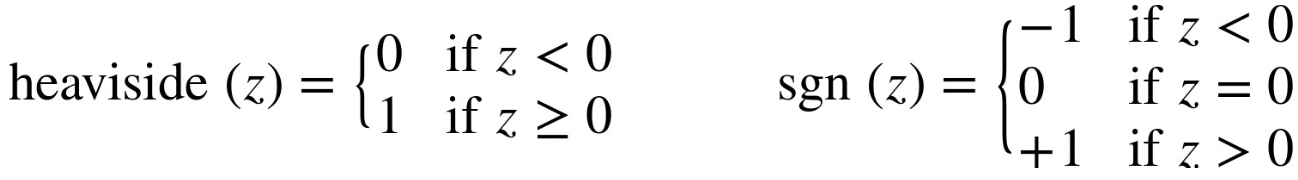
Multilayer network
When we stack this units together into layers, we get a multilayer artificial neural network
Learning rules
Classification example:
XOR function
Let us suppose that we want to create a two layer neural network able to classify these observations.
Learning rules
Classification example:
XOR function
Or equivalently, we want a neural network able to create a classification region such as the yellow one.

Learning rules
Classification example:
XOR function
Proposed solution
Learning rules
Learning rules
Activation functions
Activation function

More complex activation functions
Activation function

Backpropagation
Backpropagation
Now our objective is to train our network with a gradient based method, and to somehow propagate the errors to the previous layers

Backpropagation

Of course, with more complex architectures, the problem of computing gradients becomes an issue
Backpropagation
