indeks siły

Shapleya-Shubika

indeks siły Shapleya-Shubika

Jeden ze wskaźników służących przedstawieniu siły politycznej aktora uczestniczącego w procesie decyzyjnym w ramach ciała kolegialnego, zaproponowany w roku 1954 przez autorów od których nazwisk przyjął swą nazwę.

indeks siły Shapleya-Shubika

Czym są

indeksy/wskaźniki siły?

indeks siły Shapleya-Shubika

Indeksy siły najprościej można zdefiniować jako:

funkcje, które określają pozycję poszczególnych uczestników zgromadzenia podejmującego decyzję ze względu na zapotrzebowanie na nich przy tworzeniu koalicji wygrywających

M. Jasiński, Czy zawsze większy jest silniejszy,
czyli jak zmierzyć siłę uczestników zgromadzeń
decyzyjnych, „Studia Socjologiczne” 2000,
nr 1-2(156-157), s. 50.

indeks siły Shapleya-Shubika

Indeks siły Shapleya-Shubika jest jednym z tzw.

indeksów a priori

tzn. traktujących każdy wariant koalicji jako równie prawdopodobny, niezależnie od faktycznego dystansu ideologicznego między graczami, relacji personalnych etc.

indeks siły Shapleya-Shubika

O badaniu odległości ideologicznej między graczami oraz współczynnikach spoza grupy a priori:

M. Mazurkiewicz, J. Mercik, Modified Shapley–Shubik Power Index for Parliamentary Coalitions, „Badania Operacyjne i Decyzje” 2005, nr 2, s. 43-52.
M. Bożykowski, M. Jasiński, Struktura cząstkowej jednolitości graczy a ich znaczenie w zgromadzeniu. Hybrydowe indeksy siły, „Decyzje” 2014, nr 2, s. 5-29.
M. Jasiński, Przestrzeń ideologiczna oparta na politycznych faktach, „Decyzje” 2012, nr 17, s. 5-28.

indeks siły Shapleya-Shubika

Grę w ciele kolegialnym zapiszemy w postaci:

{q: si; sj; sk}

gdzie:

si oznacza wagę gracza i (liczbę mandatów danego ugrupowania)
q wagę wymaganą od koalicji żeby była koalicją zwycięską. Podzbiór uczestników gry stanowi koalicję.

indeks siły Shapleya-Shubika

Koalicja jest koalicją wygrywającą jeśli suma wag tworzących ją graczy jest nie mniejsza niż q. Jeżeli w wyniku przyłączenia gracza i do koalicji przegrywającej (o wadze niższej niż q) staje się ona koalicją wygrywającą, gracza i określamy jako posiadającego pozycję decydującą (wyborcę decydującego).

indeks siły Shapleya-Shubika

Wartość indeksu siły Shapleya-Shubika dla gracza i (φi) jest równa odsetkowi koalicji (uwzględniając kolejność ich budowania), w których gracz i jest graczem decydującym.

indeks siły Shapleya-Shubika

φ {phi}

indeks siły Shapleya-Shubika

Współczynnik ten posiada kilka istotnych cech:

Wartość φi zawiera się w przedziale od 0 do 1, co pozwala na wykorzystanie go w analizie porównawczej.
Suma wartości φ dla wszystkich graczy w danej grze jest równa 1.
Jeżeli φi=1, gracz i posiada pełną kontrolę nad procesem decyzyjnym w danym organie. Takiego gracza określa się mianem dyktatora.
Jeżeli φi=0, gracz i jest graczem nieistotnym,. Tj. nie istnieje żadna koalicja wygrywająca powstała przez przyłączenie się gracza i do koalicji przegrywającej.

indeks siły Shapleya-Shubika

Dla indeksu siły Shapleya-Shubika można wskazać alternatywę w postaci analizy prostszego (i bardziej intuicyjnego) współczynnika jakim jest udział w zbiorze mandatów.

Czy miałoby to sens?

indeks siły Shapleya-Shubika

Dla indeksu siły Shapleya-Shubika można wskazać alternatywę w postaci analizy prostszego (i bardziej intuicyjnego) współczynnika jakim jest udział w zbiorze mandatów.

Należy jednak zaznaczyć, że prowadziłoby to każdorazowo do uzyskania innych wyników, których wartość poznawcza byłaby ograniczona.

indeks siły Shapleya-Shubika

Częstość uzyskiwania udziału w zbiorze mandatów uniemożliwiającego zbudowanie minimalnej koalicji wygrywającej nie jest równa częstości uzyskania zerowego udziału w zbiorze mandatów, choć uzyskanie wyniku si=0 bez najmniejszych wątpliwości skutkuje uzyskaniem pozycji gracza nieistotnego.

indeks siły Shapleya-Shubika

φi=0 można jednakże uzyskać nawet mimo uzyskania mandatów. Co więcej, nie dotyczy to wyłącznie sytuacji, w których inne ugrupowanie (niż partia prezydencka) uzyskuje samodzielną większość mandatów. Przyjrzyjmy się następującemu podziałowi mandatów i jego konsekwencjom:

{12: 8; 7; 5; 3}

{12: 8; 7; 5; 3}

Ile jest możliwych koalicji (kombinacji)?.
W ilu wariantach poszczególni gracze uzyskują pozycję decydującą?
Ile wynosi siła φi?

{12: 8; 7; 5; 3}

Liczba możliwych permutacji wynosi 4!=24.
Liczba wariantów, w których poszczególni gracze uzyskują pozycję decydującą wynosi odpowiednio: {8; 8; 8; 0}
φi = {0,333; 0,333; 0,333; 0}.

{12: 8; 7; 5; 3}

Mimo uzyskania przez czwarty z komitetów 3 mandatów w 23-osobowym składzie rady (13,04%), nie istnieje ani jedna minimalna koalicja wygrywająca powstała przez dodanie tego ugrupowania do koalicji przegrywającej. Koalicja utworzona przez dowolnych dwóch spośród trzech silniejszych graczy jest koalicją wygrywającą, przyłączenie kolejnego gracza byłoby więc nieuzasadnione.

indeks siły Shapleya-Shubika

Czy uzyskiwanie najwyższego potencjału koalicyjnego (niezależne od podejścia do sytuacji remisów) jest tożsame z uzyskaniem najwyższej liczby mandatów?

indeks siły Shapleya-Shubika

Uzyskiwanie najwyższego potencjału koalicyjnego (niezależne od podejścia do sytuacji remisów) nie jest tożsame z uzyskaniem najwyższej liczby mandatów.

Wartość indeksu siły Shapleya-Shubika, a co za tym idzie – potencjał koalicyjny, jest zależna od konkretnego rozkładu wag między poszczególnych graczy, nie jedynie od udziału gracza rozpatrywanego.

Przyjrzyjmy się następującemu podziałowi mandatów i jego konsekwencjom:

{8: 7; 7; 1}

{8: 7; 7; 1}

Ile jest możliwych koalicji (kombinacji)?.
W ilu wariantach poszczególni gracze uzyskują pozycję decydującą?
Ile wynosi siła φi?

{8: 7; 7; 1}

Liczba możliwych permutacji wynosi 3!=6.
Liczba wariantów, w których poszczególni gracze uzyskują pozycję decydującą wynosi odpowiednio:
{2; 2; 2} (koalicja każdych dwóch graczy jest koalicją wygrywającą)
φi = {0,333; 0,333; 0,333}.

Siła każdego z graczy jest równa mimo wyraźnej (siedmiokrotnej!!!!) różnicy w udziale w zbiorze mandatów.

indeks siły Shapleya-Shubika

Aby rozwiać wątpliwości dotyczące poprzedniego przykładu, rozpatrzmy scenariusz w którym nie występują remisy w liczbie mandatów:

{8: 6; 5; 4}

{8: 6; 5; 4}

φ dla wszystkich graczy ponownie będzie identyczny ({0,333; 0,333; 0,333}). Mimo, że pierwszy z graczy uzyskał samodzielną większość względną mandatów (większość względną z wykluczeniem remisów), jego faktyczna siła mierzona indeksem siły Shapleya-Shubika nie przekracza siły każdego z pozostałych dwóch graczy.

indeks siły Shapleya-Shubika

Zadanie 1:

Obliczenie wartości indeksu siły Shapleya-Shubika dla partii w polskim Sejmie w składzie wybranym w 2019 r.

PiS: 235
KO: 134
SLD: 49
PSL: 30
KONF: 11
MN: 1

indeks siły Shapleya-Shubika

Zadanie:

Wartości indeksu siły Shapleya-Shubika dla partii w polskim Sejmie w składzie wybranym w 2019 r.

PiS: 1
KO: 0
SLD: 0
PSL: 0
KONF: 0
MN: 0

indeks siły Shapleya-Shubika

Zadanie 2:

Obliczenie wartości indeksu siły Shapleya-Shubika dla partii w polskim Senacie w składzie wybranym w 2019 r.

PiS: 48
KO: 43
PSL: 3
SLD: 2
Demokracja Obywatelska: 1
Lidia Staroń: 1
Krzysztof Kwiatkowski: 1
Wadim Tyszkiewicz: 1

indeks siły Shapleya-Shubika

Zadanie 2:

Obliczenie wartości indeksu siły Shapleya-Shubika dla partii w polskim Senacie w składzie wybranym w 2019 r.

(8! = 40.320)

PiS: 0.553572
KO: 0.110714
PSL: 0.110714
SLD: 0.086905
DB: 0.034524
LS: 0.034524
KK: 0.034524
WT: 0.034524

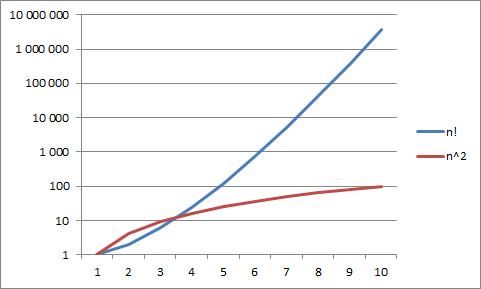
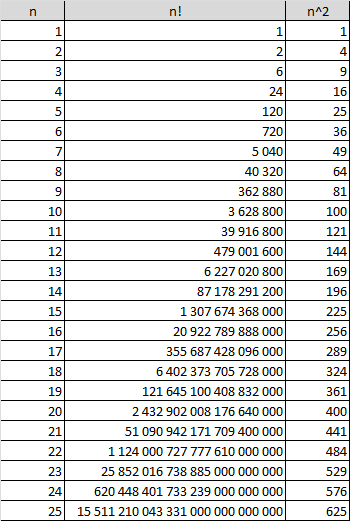
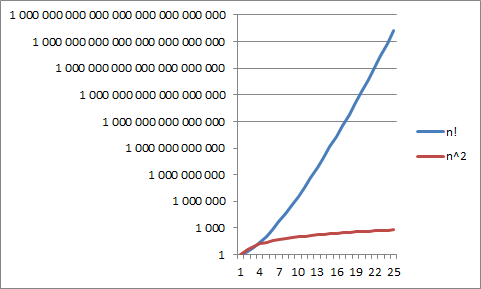
indeks siły Shapleya-Shubika

Zadanie 3:

Obliczenie wartości indeksu siły Shapleya-Shubika dla partii w polskim Senacie w składzie wybranym w 2019 r. ale z uwzględnieniem faktycznych bloków:

PiS: 49
KO: 46
PSL: 3
SLD: 2

indeks siły Shapleya-Shubika

Zadanie 3:

Obliczenie wartości indeksu siły Shapleya-Shubika dla partii w polskim Senacie w składzie wybranym w 2019 r. ale z uwzględnieniem faktycznych bloków:

PiS: 0.500000
KO: 0.166667
PSL: 0.166667
SLD: 0.166667