Unified quantum resource theory: A framework to understand quantum non-classicality.

Madhav Krishnan V

SID: 12910725

Supervisor : Min-Hsiu Hsieh

Co-Supervisor : Peter Rhode

Non-Classicality

Quantum

Classical

Entanglement

Superpositions

Non-local

Non-Contextual

Discord

Uncertainity

Resource Theories!

What is a resource?

Constraints

Resource

LOCC

Entanglement

Some R.T.s

  • Entanglement
  • Coherence
  • Purity
  • Asymmetry
  • Thermodynamics
  • Non-Contextuality
  • Non-Markovianity
  • Non-Locality

Unified framework:

Anshu, A. et al. arXiv:1708.00381

1. One-shot assisted concentration of coherence:

     Collaborators : Min-Hsiu Hsieh, Eric Chitambar.

2. General one-shot resource concentration:

     Collaborators : Min-Hsiu Hsieh, Eric Chitambar.

3. Error filteration using W-state encoding,

     Collaborators : Peter Rhode, Austin Lund.

Resource theory of coherence

Free Entities

Expensive Entities

\mathcal{I} = \left\{ \rho = \sum\limits_i p_i | i \rangle \langle i | \right\}
\rho\neq \sum\limits_i p_i | i \rangle \langle i |

Fixed basis

\{ | i \rangle \}
| i \rangle \langle i |
| i \rangle \langle i |
\Lambda_{\mathcal{I}} : \mathcal{I} \rightarrow \mathcal{I}
\Lambda : \Lambda \notin \Lambda_{\mathcal{I}}

1. One-shot assisted concentration of coherence:

Measure of coherence

  • Relative entropy of coherence 
C_r(\rho)
C_r(\rho) = \min\limits_{\delta\in \mathcal{I}} S( \rho \| \delta)
= S(\Delta(\rho)) - S(\rho),^1
\text{where } \Delta \text{ dephases } \rho \text{ (deletes off-diagonal terms)}
1.Winter, A., & Yang, D. : PRL 116.12, 120404, (2016)

Maximally coherent state

| \Phi_M \rangle = \sum\limits_{i =1 }^M \frac{1}{\sqrt{M}} | i \rangle

Alice

Bob

\left(| \psi \rangle^{AB} \right)^{\otimes n}
\Lambda \text{ (unrestricted)}
\Lambda_{\mathcal{I}}

One-way classical communication

\Phi_2^{\otimes m}

Assisted distillation of coherence

Why assisted?

  • Distributed scenario - remote target
  • Easy to model
  • For qubit, same as unrestricted communication
  • Biological systems
  • Quantum metrology
  • Protocols requiring high coherence

Assisted distillation of coherence

Optimal rate
S(\Delta(\rho^B))^1
n \rightarrow \infty
n = 1
1. Chitambar, E., et al. Physical review letters 116.7 (2016): 070402.
?
\text{ If } \Delta(\Phi_M) \succ \Delta(\psi) :

Proof Sketch direct

\psi
\Phi_M
\Lambda_{\mathcal{I}}
=S_{min}(\Delta(\psi))
\log_2M
M
Winter, A., & Yang, D. : PRL 116.12, 120404, (2016)
\cdot \psi
\cdot \Lambda(
\cdot \Phi_{\overline{M}}
\cdot\overline{\psi}
\epsilon
\epsilon^{\prime}
\text{with } \epsilon^{\prime} \text{ error, optimal}
\text{rate } M^*, \text{ will be max }
\text{over}
\text{ball}
\text{around } \psi
\log_2M^* \geq \max\limits_{\overline{\psi} \in b_*(\psi, \epsilon)}S_{min}(\Delta(\overline{\psi}))
\psi
)
\Lambda
\Lambda

Proof Sketch: Converse

\text{Starting with an operator identity :}
\Phi_M \delta \Phi_M = \frac{1}{M}\Phi_M
\delta \in \mathcal{I}
\delta
\bullet \text{ Assume the optimal rate with error } \epsilon \text{ is } M, \text{ acheived by } \Lambda
\log_2M \leq \min\limits_{\gamma \in \mathcal{I}} \left\{ -\log_2\text{Tr}(\overline{\psi}\gamma) \right\}
\overline{\psi} \text{ depends on } \Lambda, \Phi_M, \psi
\overline{\psi}
\cdot \psi
\cdot \overline{\psi}
= S_{min}(\Delta(\overline{\psi}))
2\epsilon
\log_2 M \leq \max\limits_{\overline{\psi} \in b_*^{\prime}(\psi, 2\epsilon)} S_{min}(\Delta(\overline{\psi}))

Pure state concentration

C_c(\psi, \epsilon) := \max\limits_{M \in \mathbb{N}} \left\lbrace \log_2 M : \max\limits_{\Lambda \in \mathcal{O}} F^2(\Lambda(\psi), \Phi_{M}) \geq 1- \epsilon \right\rbrace
\max\limits_{\overline{\psi} \in b_*(\psi, \epsilon)} S_{min}(\Delta(\overline{\psi})) - \delta \leq C_{c}(\psi, \epsilon) \leq \max\limits_{\overline{\psi} \in b^{\prime}_*(\psi, 2\epsilon)} S_{min}(\Delta(\overline{\psi}))
F^2(\Lambda(\psi), \Phi_{M}) \geq 1- \epsilon
\max\limits_{\Lambda \in \mathcal{O}} F^2(\Lambda(\psi), \Phi_{M}) \geq 1- \epsilon

Ensemble concentration

C_c(\mathfrak{E}, \epsilon) := \max\limits_{M \in \mathbb{N}} \left\lbrace \log_2M : \max\limits_{ \lbrace\Lambda_{i}\rbrace_i} F^{2}\left(\sum\limits_{i}p_i\Lambda_i(\psi_i), \Phi_{M} \right) \geq 1 - \epsilon \right\rbrace
\bullet \text{ Let }\mathfrak{E} = \{ p_i, \psi_i \} \text{ be a pure state ensemble}
\max\limits_{\overline{\mathfrak{E}} \in b(\mathfrak{E}, \epsilon)}F_{min}^{\Delta}(\overline{\mathfrak{E}}) - \delta \leq C_{c}(\mathfrak{E}, \epsilon) \leq \max\limits_{\overline{\mathfrak{E}} \in b(\mathfrak{E}, 2\epsilon)} F_{min}^{\Delta}(\overline{\mathfrak{E}})
\text{where, } F^{\Delta}_{min}(\mathfrak{E}) = \min\limits_{\psi_i \in \mathfrak{E}} S_{min}(\Delta(\psi_i))

Asymptotic limit

\bullet \text{ The coherence of assistance is defined as,}
D_a(\rho^B) = \max\limits_{\mathfrak{E}_{\rho}=\lbrace p_i, \psi_i \rbrace_i} \sum\limits_i p_i S(\Delta(\psi_i)) = S(\Delta(\rho^B))^1
Chitambar, E., et al. Physical review letters 116.7 (2016): 070402.
C_a(\rho, \epsilon) = \max\limits_{\mathfrak{E}_{\rho}} C_{c}(\mathfrak{E}_{\rho}, \epsilon)
\lim\limits_{\epsilon \rightarrow 0}\lim\limits_{n \rightarrow \infty}\frac{1}{n} C_a(\rho^{\otimes n}, \epsilon) = \lim\limits_{n \rightarrow \infty}\frac{1}{n}D_a(\rho^{\otimes n})

References:

  • Streltsov, A., Adesso, G., & Plenio, M. B. (2017).  Reviews of Modern Physics, 89(4), 041003.
  • Baumgratz, T., Cramer, M., & Plenio, M. B. (2014).  Phys. Rev. Lett., 113(14), 140401.
  • Winter, A., & Yang, D. (2016).  Phys. Rev. Lett., 116(12), 120404.
  • Chitambar, E., Streltsov, A., Rana, S., Bera, M. N., Adesso, G., & Lewenstein, M. (2016) Phys. Rev. Lett., 116(7), 070402.
  • Buscemi, F., & Datta, N. (2013). IEEE Trans. Inf. Th., 59(3), 1940-1954.

2. General one-shot resource concentration

\Phi_M \delta \Phi_M = \frac{1}{M}\Phi_M \hspace{0.5cm} \forall \delta \in \mathcal{I}

For coherence :

Arbitrary R.T. with MRS

\Phi^n = \Phi_2^{\otimes n} ,
\Phi^n \delta \Phi^n \leq \frac{1}{2^n}\Phi^n \hspace{0.5cm} \forall \delta \in \mathcal{F}

Leads to distillation upper-bound

Theorem: For any R.T. such that

\Phi^n \gamma \Phi^n \leq \frac{1}{2^n}\Phi^n \hspace{0.5cm} \forall \gamma \in \mathcal{F}

The optimal distillation rate m with error

\rho \rightarrow \Phi^m
m \leq \max\limits_{\overline{\rho} \in B_*^{\prime}(\rho, 2\epsilon)} G_{min}(\overline{\rho})

where, 

G_{min}(\rho) = \min\limits_{\gamma \in \mathcal{F}} \left\{ -\log_2 \text{Tr}(\rho \gamma) \right\}
\epsilon

For 

is

R.Theory Entanglement Coherence Purity
G_{min}(\psi)
S_{min}(\rho_{\psi})
S_{min}(\Delta({\psi}))
m

Concentration of m copies of MRS from a pure state 

\psi
G_{min}(\rho)
S_{min}(\Delta({\rho}))
  • General achievability in terms of 
G_{min}(\rho)
\Lambda(X) = \text{Tr} [(I-\psi)X]\pi + \text{Tr}[\psi X] \Phi^m

A map we are trying out

Ongoing work

  • Considering    resource non-generating maps
  • Understanding which R.T.s can be included in our framework
\epsilon

3. Error filteration using W-state encoding,

 

  • Error correction - redundancy

Eg:

\alpha | 0 \rangle + \beta |1 \rangle \rightarrow \alpha | 00...0 \rangle + \beta |11...1 \rangle

GHZ states:

\frac{1}{\sqrt{2}} ( | 00...0 \rangle + |11...1 \rangle )
  • Error correction
  • Cryptography
  • Communication
  • Not robust against loss.

W-states

  • Superposition of single excitation

Eg:

|W^3 \rangle = \frac{1}{\sqrt{3}} (|1 0 0 \rangle + | 0 1 0 \rangle + | 0 0 1 \rangle )
|W_i^N \rangle = \hat\mathrm{QFT_N} | vac \rangle
  • Single photon passive linear optics system
  • Atomic Ensembles 
\text{Tr}_i(|W^N \rangle \langle W^N |) = \frac{N-1}{N} | W^{N-1} \rangle \langle W^{N-1} | + \frac{1}{N} | vac \rangle \langle vac |

Protocol

 Random phase error on each mode

e^{i\theta_0}
e^{i\theta_1}
e^{i\theta_2}
0
1
2
\mathcal{E}^{\vec\theta} :
\phantom{x}^{\theta_0}
\phantom{x}^{\theta_1}
\phantom{x}^{\theta_2}

Normally distributed as 

N(\delta, 0)
| W \rangle
| W^{\vec\theta} \rangle

Averaging the error channel gives

\overline{\mathcal{E}^{\vec\theta}} (| W \rangle \langle W |) = \int p(\vec\theta) | W^{\vec\theta} \rangle \langle W^{\vec\theta} | d\theta
= e^{-\delta^2} | W \rangle \langle W | + (1 - e^{-\delta^2}) \Delta(|W \rangle \langle W |)

Dephasing channel

P_{H} =\eta + (1 -\eta) \left\{ e^{-\delta^2} + \frac{2}{N}(1 - e^{-\delta^2}) \right\}

With a loss rate

\eta

, the heralding probability will be

For a logical input 

| L \rangle = \alpha |0 \rangle + \beta | 1 \rangle
F_H = (1 - \eta) \times \frac{e^{-\delta^2} + (1 - e^{-\delta^2})\frac{1 + 2|\alpha|^2|\beta|^2}{N} }{e^{-\delta^2} + \frac{2}{N}(1 - e^{-\delta^2}) }

, the heralded fidelity is

\eta = 0.5, |\alpha| = \frac{1}{\sqrt{2}}

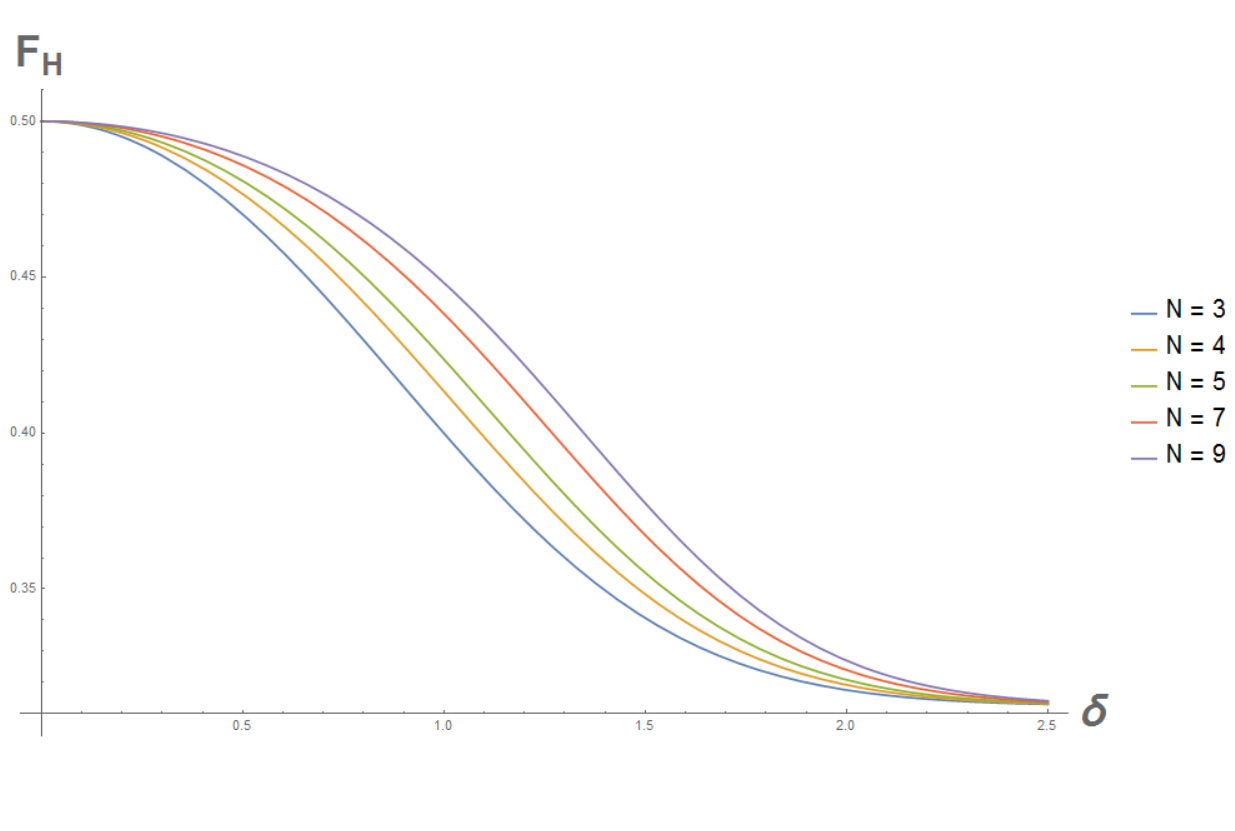
Ongoing work

  • Relation to quantum memory architectures
  • Reframing in terms of T1, T2 times.

Conclusions

  • Calculated bounds forone-shot assisted coherence concentration and recovered known asymptotic limits.
  • Proved a generalized resource distillation upper-bound and working on the achievability.
  • Developed a protocol for W-state encoded error correction and exploring applications to quantum memories 

Future Directions

  • Open problems in coherence R.T.
  • Generalized resource framework
  • Quantum optical non-classicality as a resource theory
  • Cluster states - Entanglement swapping

Thank you!

Method of the proof

  • The assisted distillation task can be broken down into two parts
  1. Alice performs POVM            on her part of the shared state          and sends the result to Bob.
\psi^{AB}
\{ P^A_i\}

2. Bob  performs an Incoherent operation           on his part of the state based on              Alice's outcome. 

\Lambda_i
  • The best strategy is for Alice to create an optimal ensemble on Bob's side and for Bob to optimally distill this ensemble
  • We need to calculate the optimal concentration rate for an ensemble of pure states
\mathfrak{E} = \{ p_i, \psi_i \}
Made with Slides.com