1.6 The Perceptron Model

Your first model with weights

Recap: MP Neuron

What did we see in the previous chapter?

(c) One Fourth Labs

Screen size (>5 in) 1 0 1 1 1 0 1 0 1 0
Battery (>2000mAh) 0 0 0 1 0 1 1 1 1 0
Like 1 0 1 0 1 1 0 1 0 0
\hat{y}
x_1
x_2
b
\hat{y}=\sum_{i=1}^n x_i \gt b

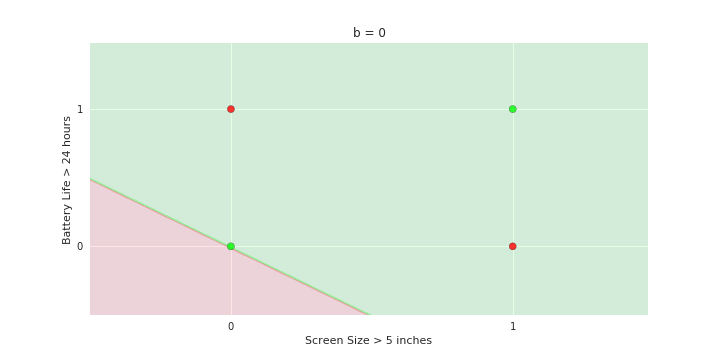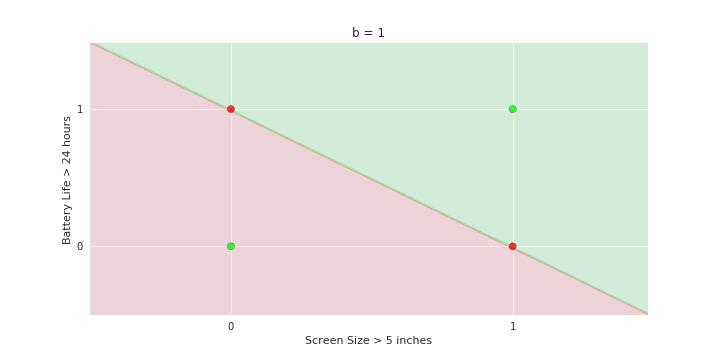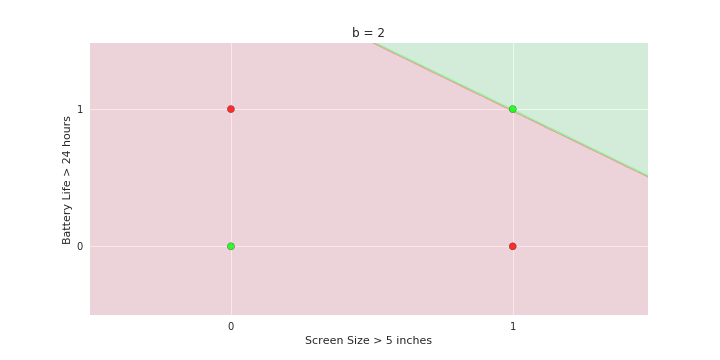
Boolean inputs

Boolean output

Linear

Fixed Slope

Few possible intercepts (b's)

The Road Ahead

What's going to change now ?

(c) One Fourth Labs

Show the six jars and convey the following by animation

-- Boolean inputs gets replaced by real inputs

-- Only one parameter b by "weights for every input" (below model jar)

-- Brute force by "our first learning algorithm"

-- Add Perceptron loss function with a saddie (not smiley)

Linear

Only one parameter, b

Real inputs

Boolean output

Brute force

The Road Ahead

What's going to change now ?

(c) One Fourth Labs

\( \{0, 1\} \)

Boolean

loss = \sum_i (y_i-\hat{y_i})^2
Accuracy=\frac{\text{Number of correct predictions}}{\text{Total number of predictions}}

Loss

Model

Data

Task

Evaluation

Learning

Linear

Only one parameter, b

Real inputs

Boolean output

Brute force

Boolean inputs

loss = \sum_i max(0,1-y_i*\hat{y_i})

Our 1st learning algorithm

Weights for every input

Data and Task

What kind of data and tasks can Perceptron process ?

(c) One Fourth Labs

Same data matrix from before with binary inputs and outputs

Animation:

- Now replace some boolean inputs by real inputs (for example, >5in will get replaced by actual screen size, >24 hours will get replaced by actual battery life and so on

- Now, highlight some columns which may seem more important than others (I will just speak through it to say that some features are more important than others

Real inputs

Data and Task

What kind of data and tasks can Perceptron process ?

(c) One Fourth Labs

Real inputs

Launch (within 6 months) 0 1 1 0 0 1 0 1 1
Weight (g) 151 180 160 205 162 182 138 185 170
Screen size (inches) 5.8 6.18 5.84 6.2 5.9 6.26 4.7 6.41 5.5
dual sim 1 1 0 0 0 1 0 1 0
Internal memory (>= 64 GB, 4GB RAM) 1 1 1 1 1 1 1 1 1
NFC 0 1 1 0 1 0 1 1 1
Radio 1 0 0 1 1 1 0 0 0
Battery(mAh) 3060 3500 3060 5000 3000 4000 1960 3700 3260
Price (INR) 15k 32k 25k 18k 14k 12k 35k 42k 44k
Like (y) 1 0 1 0 1 1 0 1 0
Launch (within 6 months) 0 1 1 0 0 1 0 1 1
Weight (<160g) 1 0 1 0 0 0 1 0 0
Screen size (<5.9 in) 1 0 1 0 1 0 1 0 1
dual sim 1 1 0 0 0 1 0 1 0
Internal memory (>= 64 GB, 4GB RAM) 1 1 1 1 1 1 1 1 1
NFC 0 1 1 0 1 0 1 1 1
Radio 1 0 0 1 1 1 0 0 0
Battery(>3500mAh) 0 0 0 1 0 1 0 1 0
Price > 20k 0 1 1 0 0 0 1 1 1
Like (y) 1 0 1 0 1 1 0 1 0

Data Preparation

Can the data be used as it is ?

(c) One Fourth Labs

Same data matrix from before with binary inputs and outputs

Animation:

- Highlight two columns which have very different ranges (say price and battery life)

- These columns are not comparable

 

- Now show one of the columns on the RHS

- Highlight the max and min values of this column

- Now show the standardized version of this column

 

- Repeat this for another column

 

- FInally replace this matrix by a standardized matrix

 

(Its ok if you need to do all of this over multiple slides)

 

 

 

 

Column1

Show one of the columns here

Standardized column

Now show the standardized value of the column here.

 

Show the computtaions

(x-min)/ (max - min)

 

(c) One Fourth Labs

Launch (within 6 months) 0 1 1 0 0 1 0 1 1
Weight (g) 151 180 160 205 162 182 138 185 170
Screen size (inches) 5.8 6.18 5.84 6.2 5.9 6.26 4.7 6.41 5.5
dual sim 1 1 0 0 0 1 0 1 0
Internal memory (>= 64 GB, 4GB RAM) 1 1 1 1 1 1 1 1 1
NFC 0 1 1 0 1 0 1 1 1
Radio 1 0 0 1 1 1 0 0 0
Battery(mAh) 3060 3500 3060 5000 3000 4000 1960 3700 3260
Price (INR) 15k 32k 25k 18k 14k 12k 35k 42k 44k
Like (y) 1 0 1 0 1 1 0 1 0
screen size
5.8
6.18
5.84
6.2
5.9
6.26
4.7
6.41
5.5
screen size
0.64
0.87
0.67
0.88
0.7
0.91
0
1
0.47

min

max

Standardization formula

x' = \frac{x-min}{max-min}
Launch (within 6 months) 0 1 1 0 0 1 0 1 1
Weight (g) 151 180 160 205 162 182 138 185 170
Screen size 0.64 0.87 0.67 0.88 0.7 0.91 0 1 0.47
dual sim 1 1 0 0 0 1 0 1 0
Internal memory (>= 64 GB, 4GB RAM) 1 1 1 1 1 1 1 1 1
NFC 0 1 1 0 1 0 1 1 1
Radio 1 0 0 1 1 1 0 0 0
Battery(mAh) 3060 3500 3060 5000 3000 4000 1960 3700 3260
Price (INR) 15k 32k 25k 18k 14k 12k 35k 42k 44k
Like (y) 1 0 1 0 1 1 0 1 0
battery
3060
3500
3060
5000
3000
4000
1960
3700
3260
battery
0.36
0.51
0.36
1
0.34
0.67
0
0.57
0.43

min

max

Data Preparation

Can the data be used as it is ?

Launch (within 6 months) 0 1 1 0 0 1 0 1 1
Weight (g) 151 180 160 205 162 182 138 185 170
Screen size 0.64 0.87 0.67 0.88 0.7 0.91 0 1 0.47
dual sim 1 1 0 0 0 1 0 1 0
Internal memory (>= 64 GB, 4GB RAM) 1 1 1 1 1 1 1 1 1
NFC 0 1 1 0 1 0 1 1 1
Radio 1 0 0 1 1 1 0 0 0
Battery 0.36 0.51 0.36 1 0.34 0.67 0 0.57 0.43
Price (INR) 15k 32k 25k 18k 14k 12k 35k 42k 44k
Like (y) 1 0 1 0 1 1 0 1 0

Data Preparation

Can the data be used as it is ?

(c) One Fourth Labs

Launch (within 6 months) 0 1 1 0 0 1 0 1 1
Weight 0.19 0.63 0.33 1 0.36 0.66 0 0.70 0.48
Screen size 0.64 0.87 0.67 0.88 0.7 0.91 0 1 0.47
dual sim 1 1 0 0 0 1 0 1 0
Internal memory (>= 64 GB, 4GB RAM) 1 1 1 1 1 1 1 1 1
NFC 0 1 1 0 1 0 1 1 1
Radio 1 0 0 1 1 1 0 0 0
Battery 0.36 0.51 0.36 1 0.34 0.67 0 0.57 0.43
Price 0.09 0.63 0.41 0.19 0.06 0 0.72 0.94 1
Like (y) 1 0 1 0 1 1 0 1 0
Launch (within 6 months) 0 1 1 0 0 1 0 1 1
Weight (g) 151 180 160 205 162 182 138 185 170
Screen size (inches) 0.64 0.87 0.67 0.88 0.7 0.91 0 1 0.47
dual sim 1 1 0 0 0 1 0 1 0
Internal memory (>= 64 GB, 4GB RAM) 1 1 1 1 1 1 1 1 1
NFC 0 1 1 0 1 0 1 1 1
Radio 1 0 0 1 1 1 0 0 0
Battery(mAh) 0.36 0.51 0.36 1 0.34 0.67 0 0.57 0.43
Price (INR) 15k 32k 25k 18k 14k 12k 35k 42k 44k
Like (y) 1 0 1 0 1 1 0 1 0
weight
0.19
0.63
0.33
1
0.36
0.66
0
0.70
0.48
battery
0.36
0.51
0.36
1
0.34
0.67
0
0.57
0.43
price
0.09
0.63
0.41
0.19
0.06
0
0.72
0.94
1
Launch (within 6 months) 0 1 1 0 0 1 0 1 1
Weight (g) 151 180 160 205 162 182 138 185 170
Screen size (inches) 0.64 0.87 0.67 0.88 0.7 0.91 0 1 0.47
dual sim 1 1 0 0 0 1 0 1 0
Internal memory (>= 64 GB, 4GB RAM) 1 1 1 1 1 1 1 1 1
NFC 0 1 1 0 1 0 1 1 1
Radio 1 0 0 1 1 1 0 0 0
Battery(mAh) 0.36 0.51 0.36 1 0.34 0.67 0 0.57 0.43
Price (INR) 15k 32k 25k 18k 14k 12k 35k 42k 44k
Like (y) 1 0 1 0 1 1 0 1 0

The Model

What is the mathematical model ?

(c) One Fourth Labs

Show the standardised data matrix

Show the model here

The Model

What is the mathematical model ?

(c) One Fourth Labs

Launch (within 6 months) 0 1 1 0 0 1 0 1 1
Weight 0.19 0.63 0.33 1 0.36 0.66 0 0.70 0.48
Screen size 0.64 0.87 0.67 0.88 0.7 0.91 0 1 0.47
dual sim 1 1 0 0 0 1 0 1 0
Internal memory (>= 64 GB, 4GB RAM) 1 1 1 1 1 1 1 1 1
NFC 0 1 1 0 1 0 1 1 1
Radio 1 0 0 1 1 1 0 0 0
Battery 0.36 0.51 0.36 1 0.34 0.67 0 0.57 0.43
Price 0.09 0.63 0.41 0.19 0.06 0 0.72 0.94 1
Like (y) 1 0 1 0 1 1 0 1 0

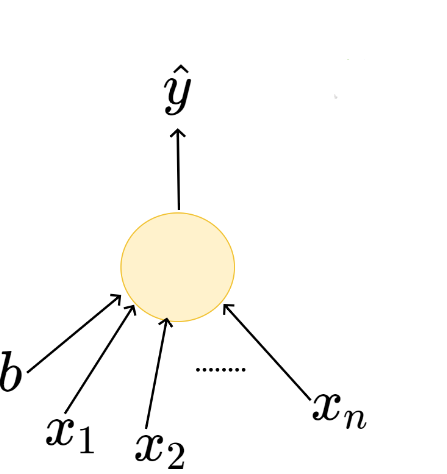
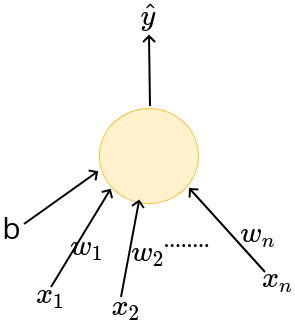
\(x_1\)

b

\(x_n\)

\(\hat{y}\)

\(x_2\)

\(w_1\)

\(w_2\)

\(w_n\)

y=\sum_{i=1}^n w_i x_i \geq b

The Model

How is this different from the Perceptron Model ?

(c) One Fourth Labs

1) Show the equations side by side of MP and perceptron and see what is changing

 

Real inputs

Linear

Weights for each input

Adjustable threshold

Boolean inputs

Linear

Inputs are not weighted

Adjustable threshold

The Model

How is this different from the Perceptron Model ?

(c) One Fourth Labs

Real inputs

Linear

Weights for each input

Adjustable threshold

Boolean inputs

Linear

Inputs are not weighted

Adjustable threshold

\hat{y}=\sum_{i=1}^n x_i \geq b
\hat{y}=\sum_{i=1}^n w_i x_i \geq b

The Model

What do weights allow us to do ?

(c) One Fourth Labs

Hard part: the examples mentioned below need to be constructed carefully

 

- Show two examples where all features are same but one has high price (no_buy) and the other has low price (buy)

- 9 terms in the sum will be same

- now if there is a negative weight attached with the price then one will cross the threshold and the other will not

- weights can be inhibitory (negative) or excitatory (positive)

Show standardised data from before. Focus on price and output and show that there is an inverse relation between them.

 

The Model

What do weights allow us to do ?

(c) One Fourth Labs

Launch (within 6 months) 0 1 1 0 0 1 0 1 1
Weight (g) 151 180 160 205 162 182 138 185 170
Screen size (inches) 5.8 6.18 5.84 6.2 5.9 6.26 4.7 6.41 5.5
dual sim 1 1 0 0 0 1 0 1 0
Internal memory (>= 64 GB, 4GB RAM) 1 1 1 1 1 1 1 1 1
NFC 0 1 1 0 1 0 1 1 1
Radio 1 0 0 1 1 1 0 0 0
Battery(mAh) 3060 3500 3060 5000 3000 4000 1960 3700 3260
Price (INR) 15k 32k 25k 18k 14k 12k 35k 42k 44k
Like (y) 1 0 1 0 1 1 0 1 0

\(x_1\)

b

\(x_n\)

\(\hat{y}\)

\(x_2\)

\(w_1\)

\(w_2\)

\(w_n\)

\hat{y}=\sum_{i=1}^n w_i x_i \geq b

\(w_{price} \rightarrow -ve\)

Like  \(\alpha  \frac{1}{price}\)

Some Math fundae

Can we write the perceptron model slightly more compactly?

(c) One Fourth Labs

 

  • Show the array of x_i’s

  • Show the array of w_i’s

  • We can think of these as vectors w and x

  • And we can say that x \in R^5 and w \in R^5

  • What is the dot product between w and x

  • Show the formula

  • Just say, that this is by definition and nothing great about it    

  • Now show the final compact dot product form of the formula

Some Math fundae

Can we write the perceptron model slightly more compactly?

(c) One Fourth Labs

x : [0, 0.19, 0.64, 1, 1, 0]

w: [0.3, 0.4, -0.3, 0.1, 0.5]

 \(\vec{x} \in R^5\)

 \(\vec{w} \in R^5\)

\( \vec{x} \)

\( \vec{w} \)

\(\vec{x}.\vec{w}\) = ?

\(\vec{x}.\vec{w} = x_1.w_1 + x_2.w_2 + ... x_n.w_n\)

w.k.t     \hat{y}=\sum_{i=1}^n w_i x_i \geq b
= \sum_{i=1}^n x_i.w_i
\hat{y}= 1 \text{ (if } \vec{x}.\vec{w} \geq b)
\hat{y}= 0 \text{ (otherwise)}

\(x_1\)

b

\(x_n\)

\(\hat{y}\)

\(x_2\)

\(w_1\)

\(w_2\)

\(w_n\)

\hat{y}=\sum_{i=1}^n w_i x_i \geq b

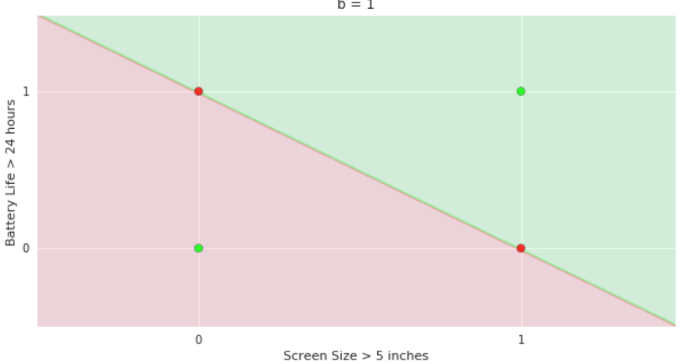
The Model

What is the geometric interpretation of the model ?

(c) One Fourth Labs

  • On LHS again recap the two variable plot for perceptron
  • show how the green and red half planes change as b=0,1,2
  • Read the remaining slides also before making this slide so that you can have a meaningful example throughout
  • On RHS show the same plot and show that now in the case of perceptron, for a given value of b we can also rotate the line by changing the slope w. and get multiple partitions of green and red half planes
  • Also show that b itself is smooth now and not restricted to values 0,1, and 2

More freedom

The Model

What is the geometric interpretation of the model ?

(c) One Fourth Labs

  • On LHS again recap the two variable plot for perceptron
  • show how the green and red half planes change as b=0,1,2
  • Read the remaining slides also before making this slide so that you can have a meaningful example throughout
  • On RHS show the same plot and show that now in the case of perceptron, for a given value of b we can also rotate the line by changing the slope w. and get multiple partitions of green and red half planes
  • Also show that b itself is smooth now and not restricted to values 0,1, and 2

More freedom

The Model

Why is more freedom important ?

(c) One Fourth Labs

  • Plot some data with two variables x1 and x2 such that the positive and negative points cannot be separated by MP model but can be separated by the perceptron model 

More freedom

The Model

Is this all the freedom that we need ?

(c) One Fourth Labs

  • On LHS show a perceptron type data plot where it is impossible to drawn any line to separate the positive points from the negative points. 
  • For example, in the case of phone think of two features such that it is fine if either of them is present but not if both are present
  • Show that we will need a complex decision surface to divide the green and red points. Take a surface such that you can write an equation for it so that we can show that instead of line we now need this complex function

We want even more freedom

  • on RHS show a data plot where there are some outliers within positive and negative clusters
  • Now show a complex surface such that we can separate the positive and negative points completely
  • Now show even more complex outliers and show you need even more complex surfaces (somewhat similar to Andrej Karpathy's plot which we have used to explain adversarial examples in the lecture on Visualize CNNs)

The Model

What if we have more than 2 dimensions ?

(c) One Fourth Labs

  • Now show a 3d plot and show how in 3d also perceptron still divides the input space into two halves - red and blue
  • I would like to have an animation which shows that as we change w_1, w_2 and b how the plane changes
  • now on RHS show one more plot here have you have some data which cannot be separated by a plane and no matter how you adjust w_1, w_2 and b you cannot separate these points
  • Again, this can be done by apparently creating a video from python itself. You can ask Harish (check with Ananya) to do this

 

Inference

How do you put this model to use ?

(c) One Fourth Labs

1. Show small training matrix here

2. Show humans with rules in his head

3. Show show one test instance here

4. Show human's output here

5 - now replace human with perceptron model and

 

6 - now replace human's output with model equations and compute the output

Loss Function

What is the loss function that you use for this model ?

(c) One Fourth Labs

First write it as this,

L = 0 if y = \hat{y}

   = 1 if y != \hat{y} 

 

Now write it more compactly as 

\indicator_{y - \hat{y}}

1. Show small training matrix here

2. Show the loss function as if-else

3. Show the loss function as indicator variable

4. Now add a column for y_hat and compute the loss

5. Now show the pink box with the QA

 

Q. What is the purpose of the loss function ?

A. To tell the model that some correction needs to be done!

Q. How ?

A. We will see soon

Loss Function

How is this different from the squared error loss function ?

(c) One Fourth Labs

First write it as this,

L = 0 if y = \hat{y}

   = 1 if y != \hat{y} 

 

Now write it more compactly as 

\indicator_{y - \hat{y}}

1. Show small training matrix here

2. Show the loss function as if-else

3. Show the loss function as indicator variable

4. Now add a column for y_hat and compute the loss

5. Now show the pink box with the QA

 

Q. What is the purpose of the loss function ?

A. To tell the model that some correction needs to be done!

Q. How ?

A. We will see soon

Loss Function

How is this different from the squared error loss function ?

(c) One Fourth Labs

1.

Show small training matrix here

Show output of model

2. squared error loss and perceptron loss formula on LHS

3. Add two columns to compute these losses one row at a time the QA

4 Show the pink box

 

 

Squared error loss is equivalent to perceptron loss when the outputs are boolean

Loss Function

Can we plot the loss function ?

(c) One Fourth Labs

- Show single variable data on LHS so that there are only two parameters w,b 

- Show model below it

- Now show a 3d-plot with w,b,error

- Substitute different values of w,b and compute output (additional column in the matrix) and loss (additional column in the matrix)

- Show how the error changes as you change the value of w,b

 

Learning Algorithm

 

What is the typical recipe for learning parameters of a model ?

(c) One Fourth Labs

Initialise 

\(w_1, w_2, b \)

Iterate over data:

\( \mathscr{L}  = compute\_loss(x_i) \)

\( update(w_1, w_2, b, \mathscr{L}) \)

till satisfied

\(\mathbf{w} = [w_1, w_2] \)

Weight Screen size Like
0.19 0.64 1
0.63 0.87 1
0.33 0.67 0
1 0.88 0

Learning Algorithm

 

What does the perceptron learning algorithm look like ?

Initialize w randomly
    while !convergence do
        Pick random x ∈ P U N
	    if y_i == 1 and w.x < b then
	         w = w + x 
	         b = b + 1
	    end
	    if y_i == 0 and w.x ≥ b then
		 w = w − x 
		 b = b - 1
	    end
    end
/*the algorithm converges when all the
inputs are classified correctly */
\hat{y}=\sum_{i=1}^n w_i x_i \geq b
\hat{y}= 1 \text{ (if } \vec{x}.\vec{w} \geq b)
\hat{y}= 0 \text{ (otherwise)}

X is also a vector!

[0.19, 0.67]

Learning Algorithm

 

Can we see this algorithm in action ?

(c) One Fourth Labs

Initialize w randomly
    while !convergence do
        Pick random x ∈ P U N
	    if y_i == 1 and w.x < b then
	         w = w + x 
	         b = b + 1
	    end
	    if y_i == 0 and w.x ≥ b then
		 w = w − x 
		 b = b - 1
	    end
    end
/*the algorithm converges when all the
inputs are classified correctly */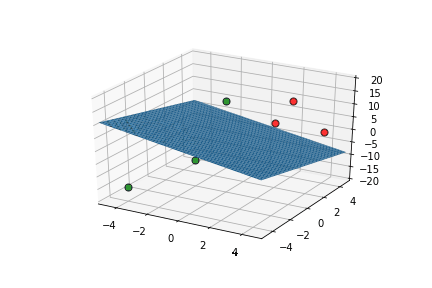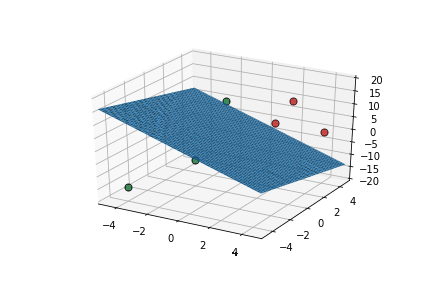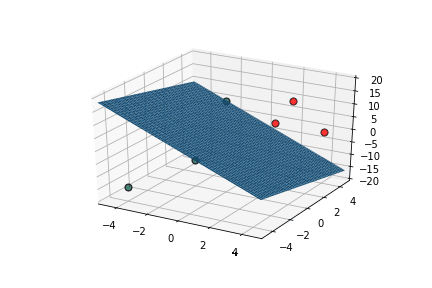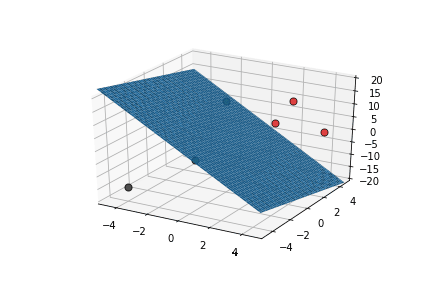
x1 x2 x3
2 2 5 10 1 1
2 4 10 17 1 1
4 4 0 11 1 1
0 0 15 14 1 0
-4 -4 -15 -15 0 0
-2 0 -10 -26 0 0
\vec{x}.\vec{w}-b
\hat{y}
y

This triggers learning!

\hat{y}= 1 \text{ (if } \vec{x}.\vec{w} \geq b)
\hat{y}= 0 \text{ (otherwise)}

Learning Algorithm

 

What is the geometric interpretation of this ?

\hat{y}=\sum_{i=1}^n w_i x_i \geq b

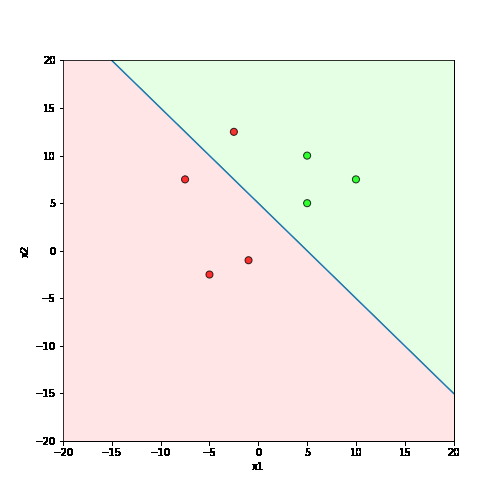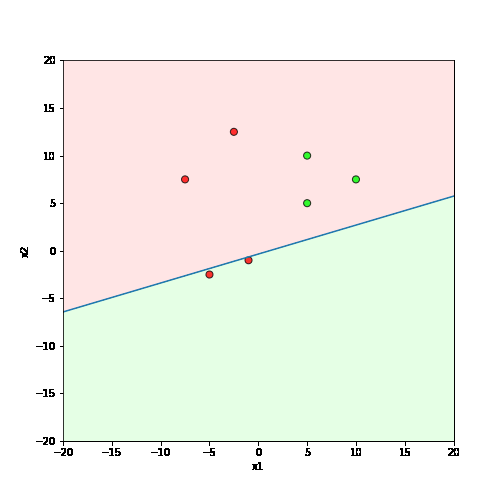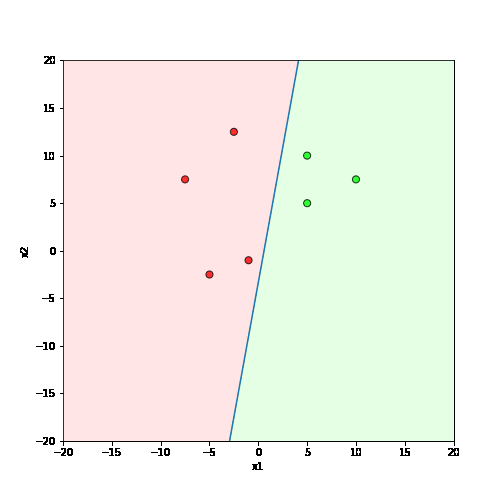
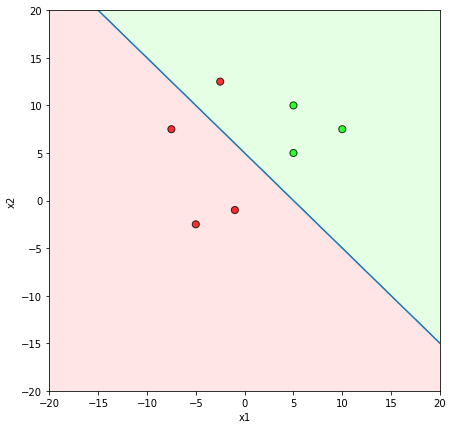
Misclassified

Let's learn!

Initialize w randomly
    while !convergence do
        Pick random x ∈ P U N
	    if y_i == 1 and w.x < b then
	         w = w + x 
	         b = b + 1
	    end
	    if y_i == 0 and w.x ≥ b then
		 w = w − x 
		 b = b - 1
	    end
    end
/*the algorithm converges when all the
inputs are classified correctly */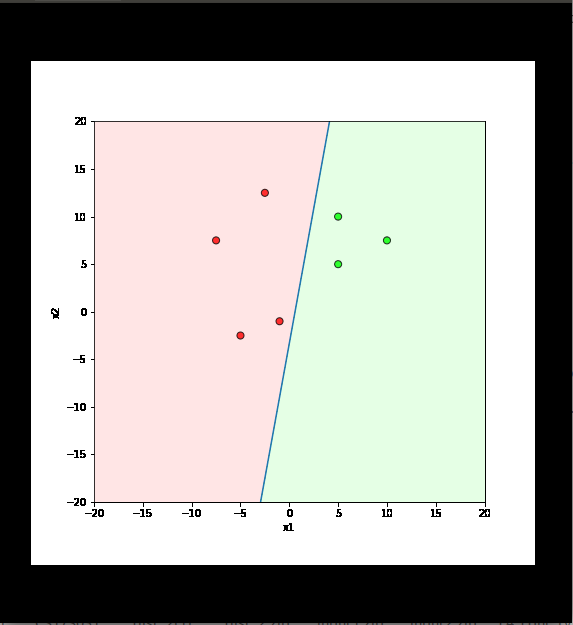

Learning Algorithm

 

What does "till satisfied" mean ?

(c) One Fourth Labs

Initialise 

\(w_1, w_2, b \)

Iterate over data:

\( \mathscr{L}  = compute\_loss(x_i) \)

\( update(w_1, w_2, b, \mathscr{L}) \)

till satisfied

\( total\_loss  = 0 \)

\( total\_loss  += \mathscr{L} \)

till total loss becomes 0

till total loss becomes < \( \epsilon \)

till number of iterations exceeds k (say 100)

Evaluation

 

How do you check the performance of the perceptron model?

(c) One Fourth Labs

Same slide as that in MP neuron

Take-aways

So will you use MP neuron?

(c) One Fourth Labs

\( \in \mathbb{R} \)

Boolean

Loss

Model

Data

Task

Evaluation

Learning

loss = \sum_i (y_i-\hat{y_i})^2
Accuracy=\frac{\text{Number of correct predictions}}{\text{Total number of predictions}}

An Eye on the Capstone project

How is perceptron related to the capstone project ?

(c) One Fourth Labs

Show the 6 jars at the top (again can be small)

 

\( \{0, 1\} \)

\( \in \mathbb{R} \)

 

Show that the signboard image can be represented as real numbers

Boolean

 

text/no-text

Show a plot with all text images on one side and non-text on another

show squared error loss

show perceptronlearning algorithm

show accuracy formula

and show a small matrix below with some ticks and crossed and show how accuracy will be calculated

The simplest model for binary classification

An Eye on the Capstone project

How is perceptron related to the capstone project ?

(c) One Fourth Labs

Show the 6 jars at the top (again can be small)

 

\( \{0, 1\} \)

\( \in \mathbb{R} \)

 

Show that the signboard image can be represented as real numbers

Boolean

 

text/no-text

Show a plot with all text images on one side and non-text on another

show squared error loss

show perceptronlearning algorithm

show accuracy formula

and show a small matrix below with some ticks and crossed and show how accuracy will be calculated

The simplest model for binary classification

\( \{0, 1\} \)

Boolean

loss = \sum_i (y_i-\hat{y_i})^2
Accuracy=\frac{\text{Number of correct predictions}}{\text{Total number of predictions}}

Loss

Model

Data

Task

Evaluation

Learning

Linear

Only one parameter, b

Real inputs

Boolean output

Brute force

Boolean inputs

loss = \sum_i max(0,1-y_i*\hat{y_i})

Our 1st learning algorithm

Weights for every input

Assignments

 

How do you view the learning process ?

(c) One Fourth Labs

Assignment: Give some data including negative values and ask them to standardize it

Made with Slides.com