Computational Geometry
基本(2D)计算几何
点/向量的定义
struct Vec{
db x,y; Vec(){} Vec(db _x, db _y){x=_x,y=_y;}
inline Vec operator + (Vec b){return Vec(x+b.x,y+b.y);}
inline Vec operator - (Vec b){return Vec(x-b.x,y-b.y);}
inline Vec operator - (){return Vec(-x,-y);}
inline db operator * (Vec b){return x*b.x+y*b.y;}
inline db operator % (Vec b){return x*b.y-b.x*y;}
inline db operator ~ (){return x*x+y*y;}
inline bool operator ==(Vec b){return fabs(x-b.x) <= EPS && fabs(y-b.y) <= EPS;}
inline bool operator !=(Vec b){return fabs(x-b.x) > EPS || fabs(y-b.y) > EPS;}
inline Vec Unit(){static db _; return _ = sqrt(x*x+y*y), Vec( x/_,y/_);}
inline Vec Norm(){static db _; return _ = sqrt(x*x+y*y), Vec(-y/_,x/_);}
inline bool Quad(){return y > EPS || (fabs(y) <= EPS && x >= -EPS);}
inline bool operator < (Vec b){return fabs(y-b.y) <= EPS ? x < b.x : y < b.y;}
}; typedef Vec Pt;
inline Vec operator / (Vec a, db k){return Vec(a.x/k,a.y/k);}
inline Vec operator * (db k, Vec a){return Vec(k*a.x,k*a.y);}
inline Vec operator * (Vec a, db k){return Vec(k*a.x,k*a.y);}
inline bool Para(Vec a, Vec b){return fabs(a%b) <= EPS;}
inline bool ToLeft(Vec a, Vec b){return b%a > EPS;}
inline void O(Pt a, char c = ' '){printf("(%.3f,%.3f)%c",a.x,a.y,c);}点积和叉积似乎不太需要讲?
向量旋转
直线/线段的定义
struct Line{
Pt p[2]; Line(){} Line(Pt a, Pt b){p[0]=a,p[1]=b;}
inline Pt& operator[](int i){return p[i];}
inline Vec v(){return p[1]-p[0];}
};
inline bool cmpang(Vec a, Vec b){return a.Quad()^b.Quad() ? a.Quad() < b.Quad() : ToLeft(b,a);}
inline bool operator < (Line a, Line b){
return Para(a.v(),b.v()) && a.v()*b.v() > EPS ? ToLeft(a[0]-b[0],b.v()) : cmpang(a.v(),b.v());
}点斜式
两点式
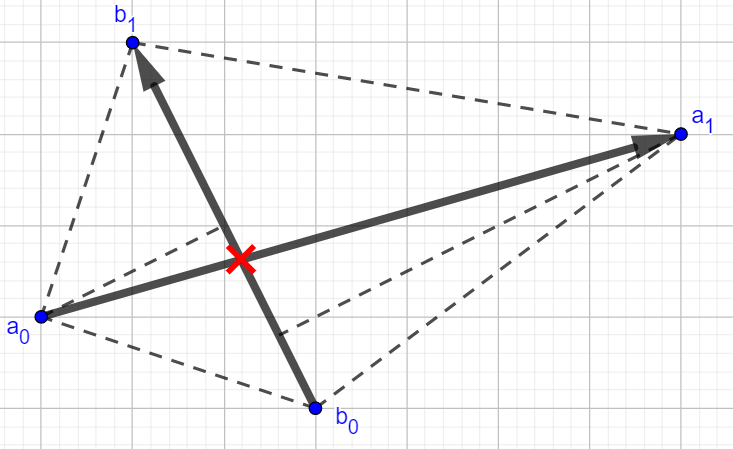
假 · 直线相交
inline Pt Cross(Line a, Line b){
static db _1, _2;
_1 = (b[0]-a[0])%(b[1]-a[0]), _2 = (b[1]-a[1])%(b[0]-a[1]);
return a[0]+_1/(_1+_2)*a.v();
}
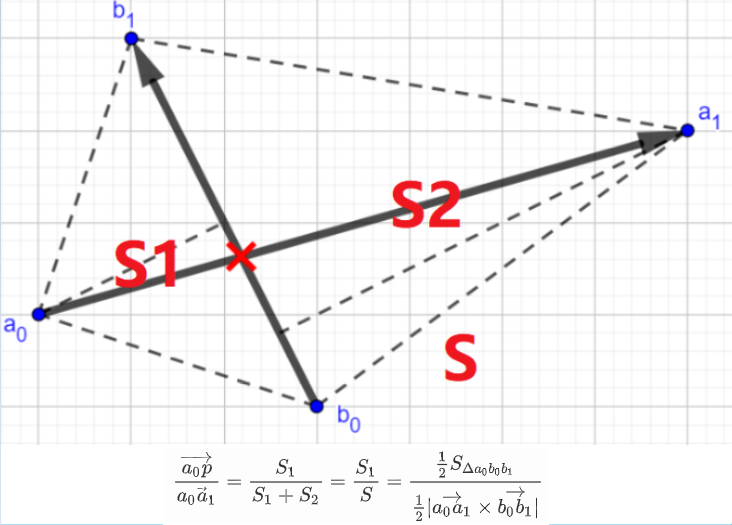
真 · 直线相交
inline Pt Cross(Line a, Line b){
return a[0]+(b.v()%(a[0]-b[0])/(a.v()%b.v()))*a.v();
}
多边形的定义
struct Poly{
Pt p[MAXN+5]; int n;
inline void clear(){n=0;}
inline Pt& operator[](int i){return p[i];}
inline Pt& back(){return p[n];}
inline void push(Pt o){p[++n] = o;}
inline void pop(){--n;}
db Area(){
if(n<3) return 0; static db _; _ = 0;
p[n+1] = p[1]; for(rint i = 1; i <= n; _ = _+p[i]%p[i+1], i++);
return fabs(_)/2;
}
};注意多边形顶点必须逆时针序存放
假·凸多边形
多边形的定义
真·凸多边形
typedef vector<Pt> Poly;
注意多边形顶点必须逆时针序存放
基本(2D)解析几何
直线相交
任意曲线相交
联立求交点
关于直线的对称点
点到直线的有向距离
解析几何的基本结论
正弦定理
余弦定理
解析几何的基本结论
海伦公式
解析几何的基本结论
射影定理
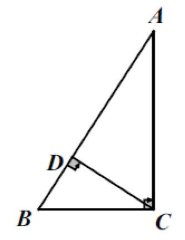
角度的计算
atan2(y,x)圆
| Situation | #Common Tangents |
|---|---|
| 0 | |
| 1 | |
| 2 | |
| 3 | |
| 4 |
进阶(2D)计算几何
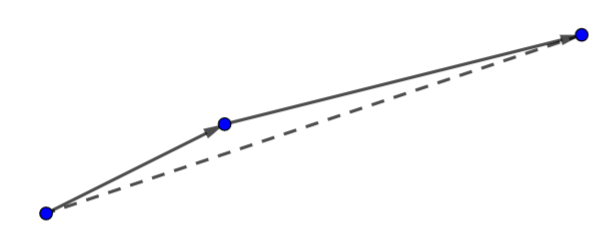
角度的比较
inline bool Para(Vec a, Vec b){return fabs(a%b) <= EPS;}
inline bool ToLeft(Vec a, Vec b){return b%a > EPS;}
inline bool cmpang(Vec a, Vec b){return a.Quad()^b.Quad() ? a.Quad() < b.Quad() : ToLeft(b,a);}
inline bool operator < (Line a, Line b){
return Para(a.v(),b.v()) && a.v()*b.v() > EPS ? ToLeft(a[0]-b[0],b.v()) : cmpang(a.v(),b.v());
}
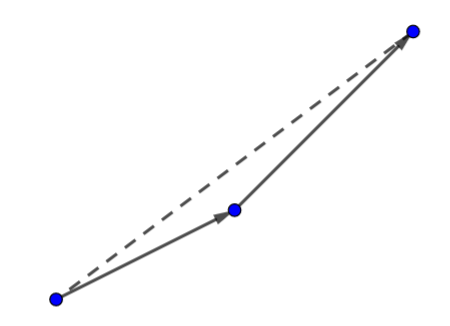
Convex-Up
Concave-Up
求凸包

求凸包

求凸包

求凸包
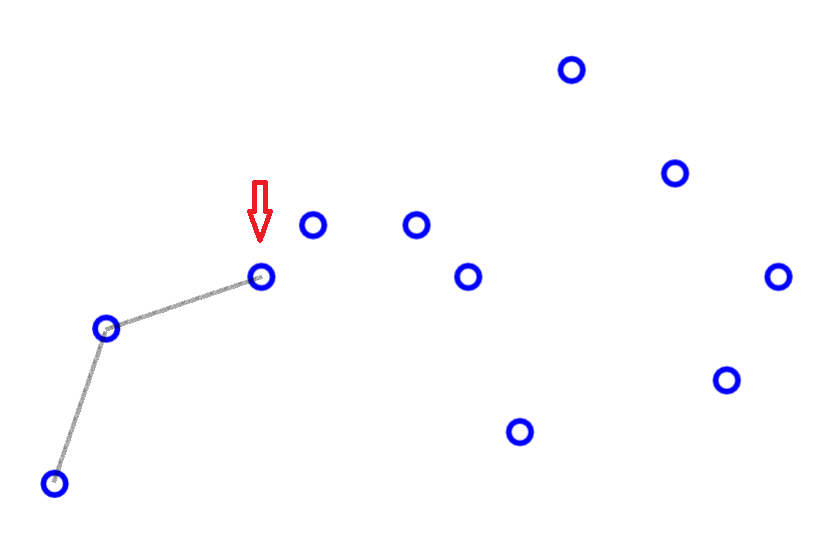
求凸包
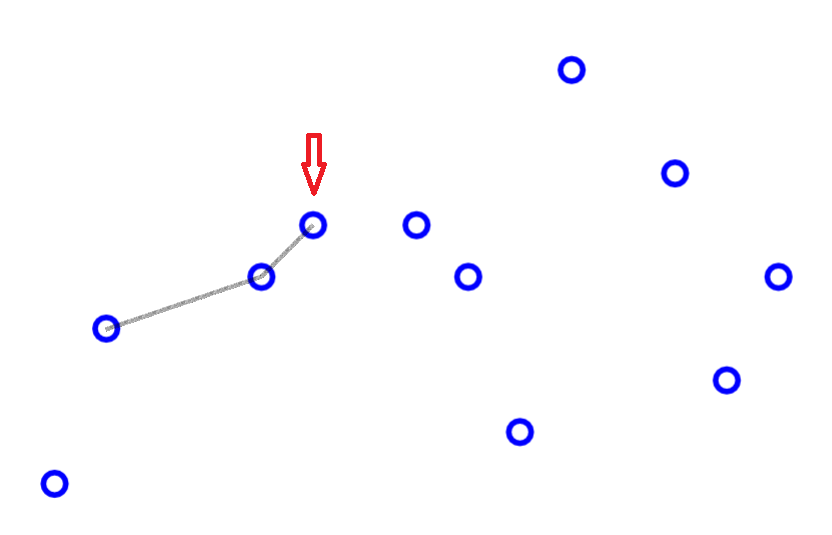
求凸包
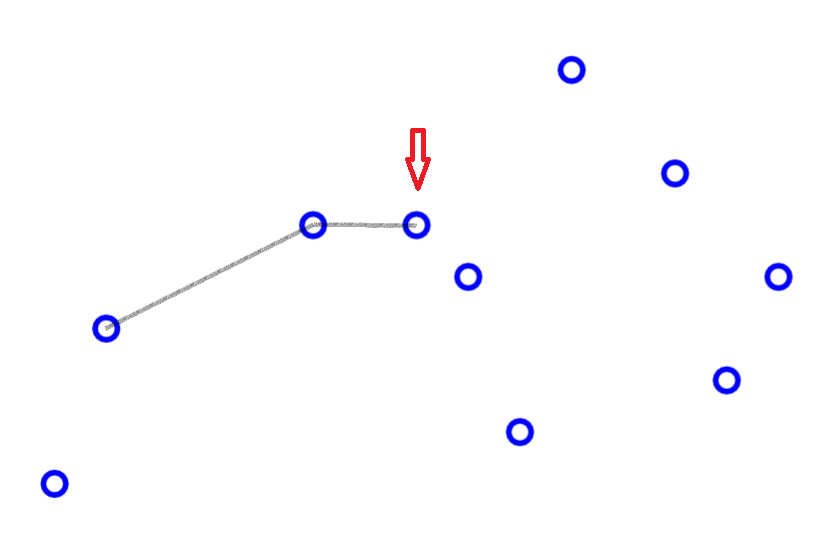
求凸包
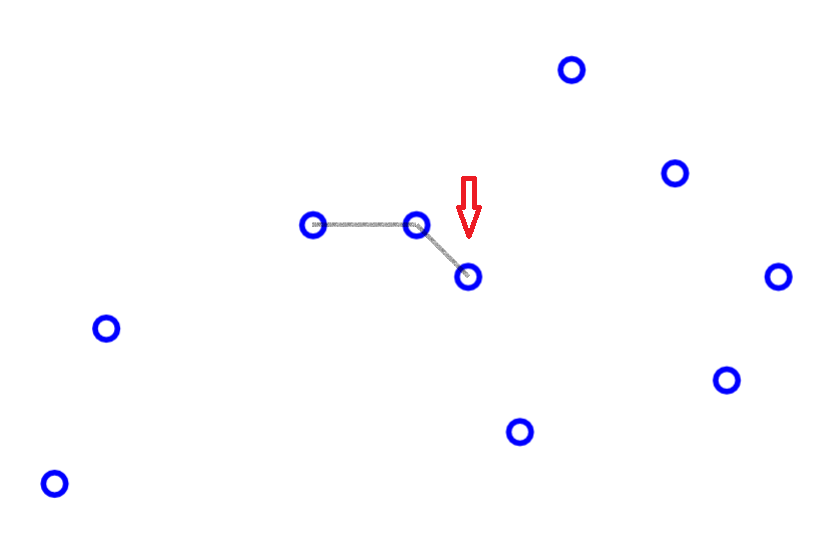
求凸包
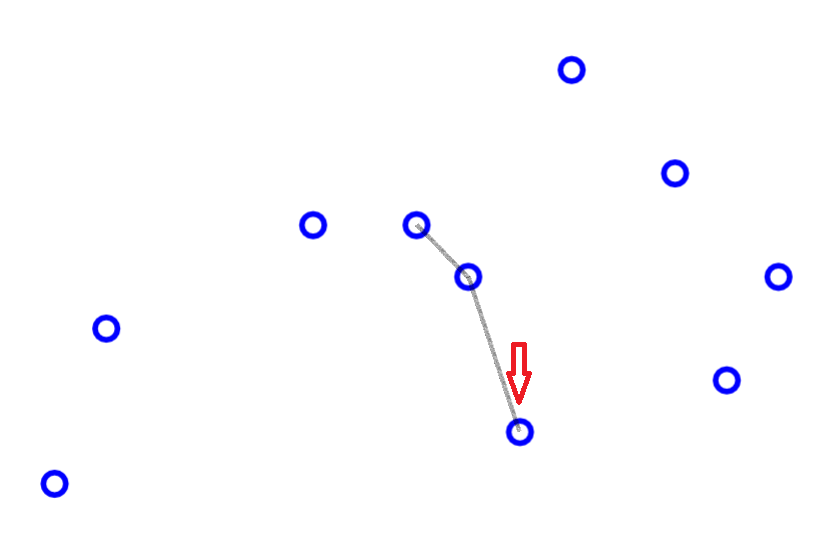
求凸包
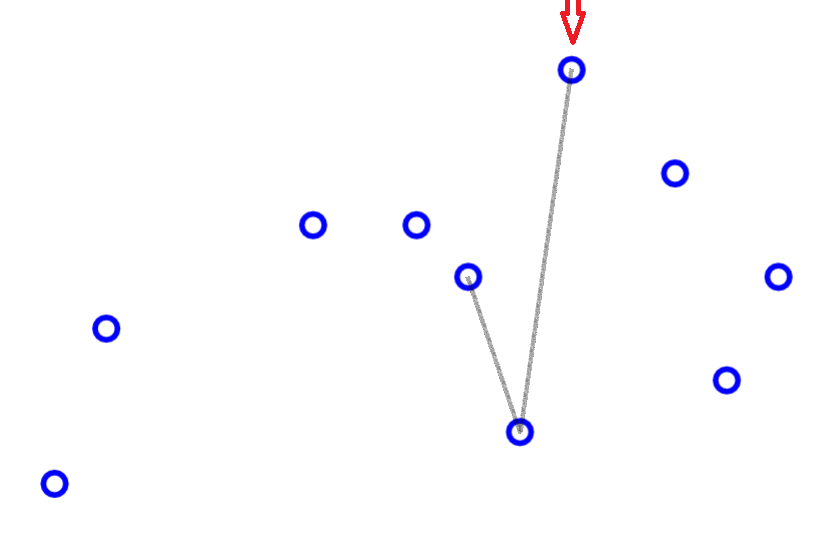
求凸包
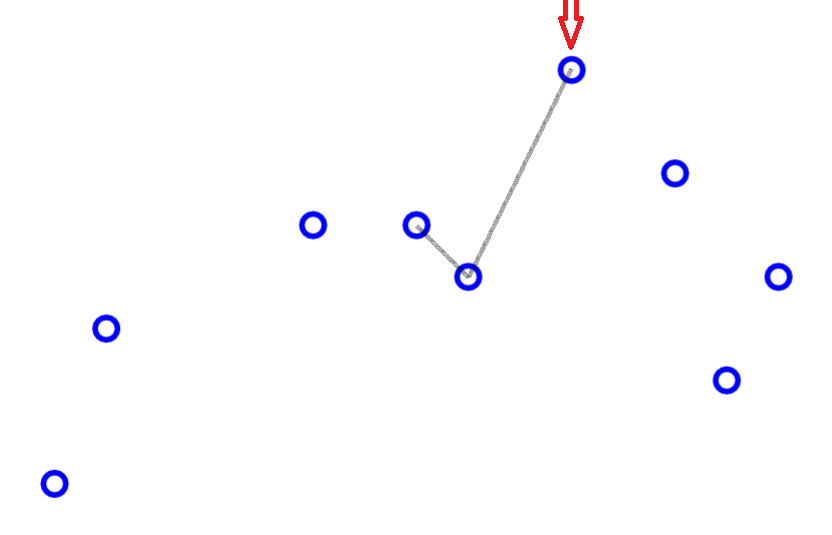
求凸包
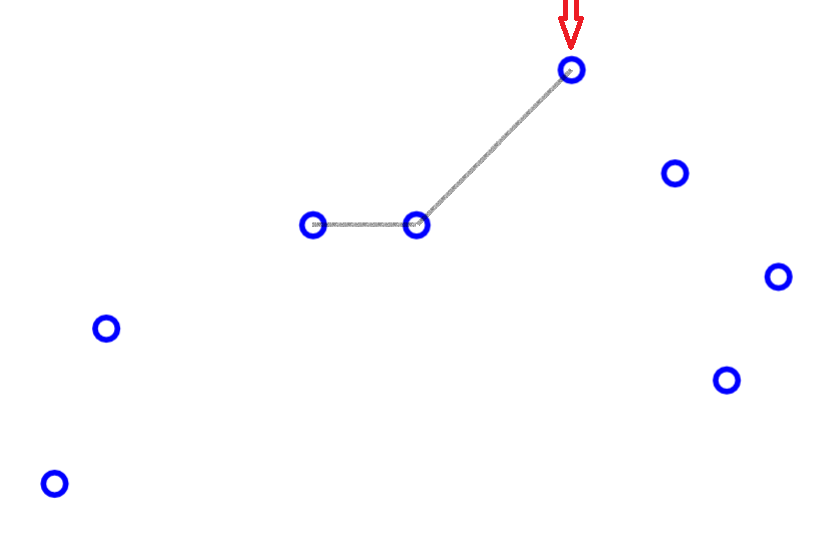
求凸包
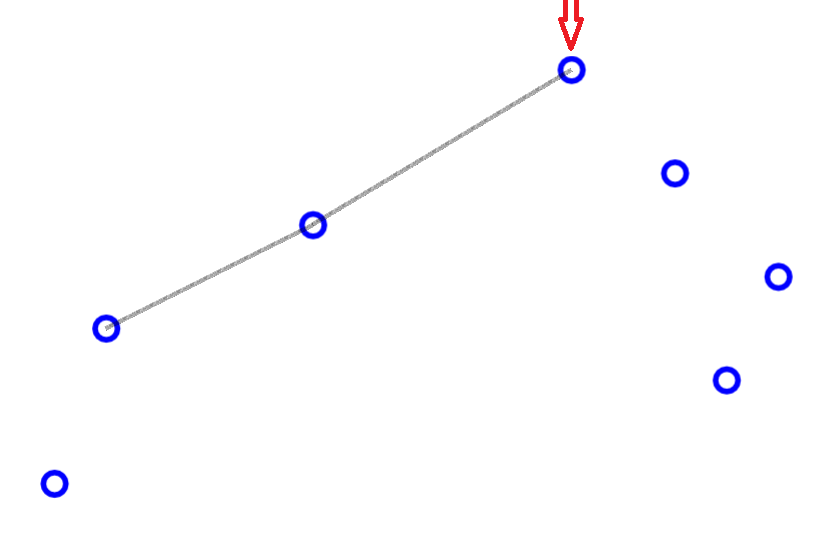
求凸包
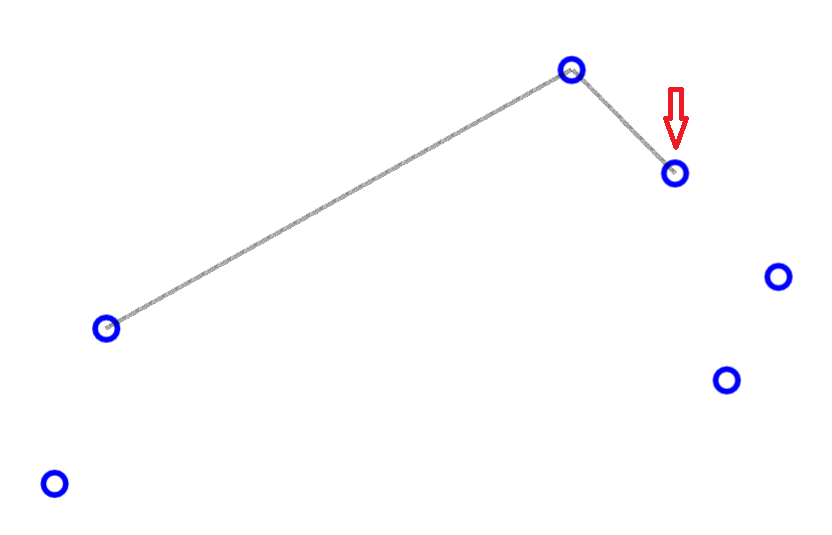
求凸包
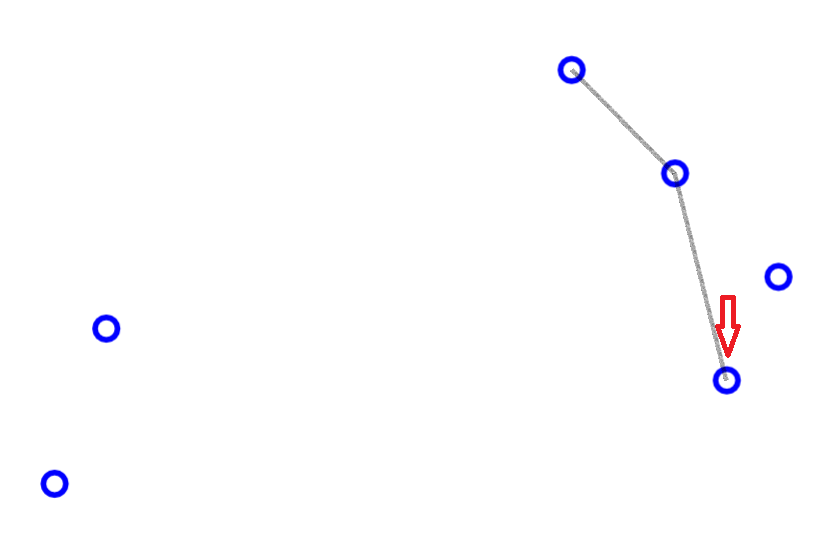
求凸包

求凸包
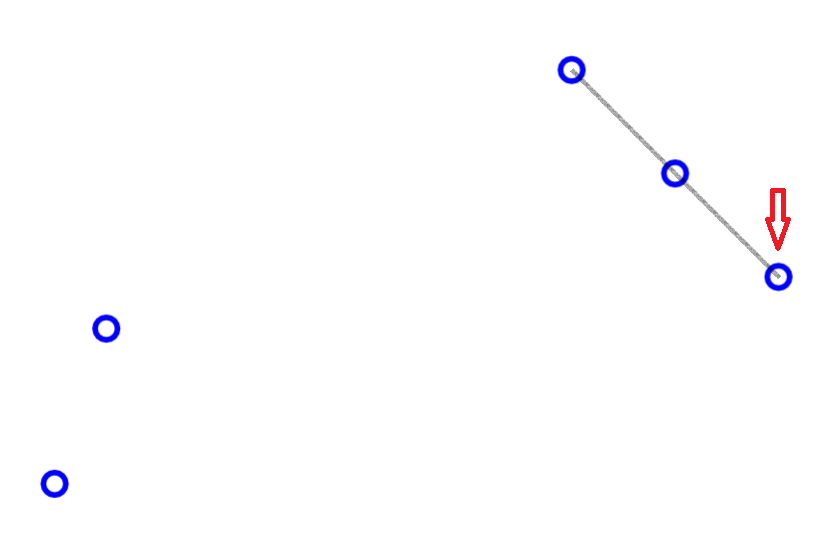
求凸包
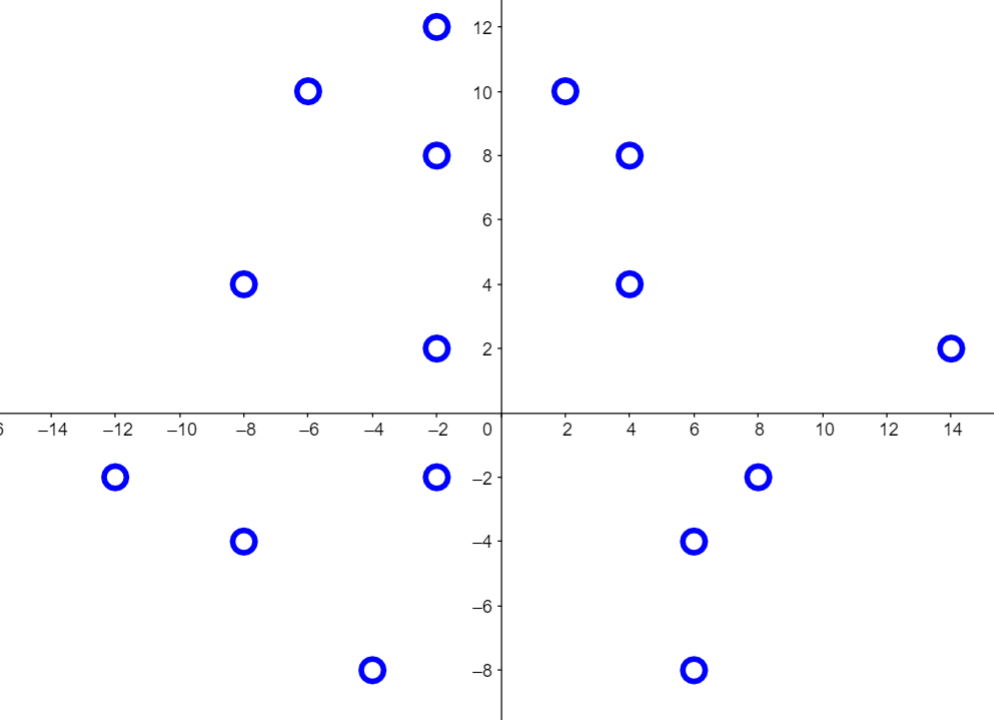
求凸包
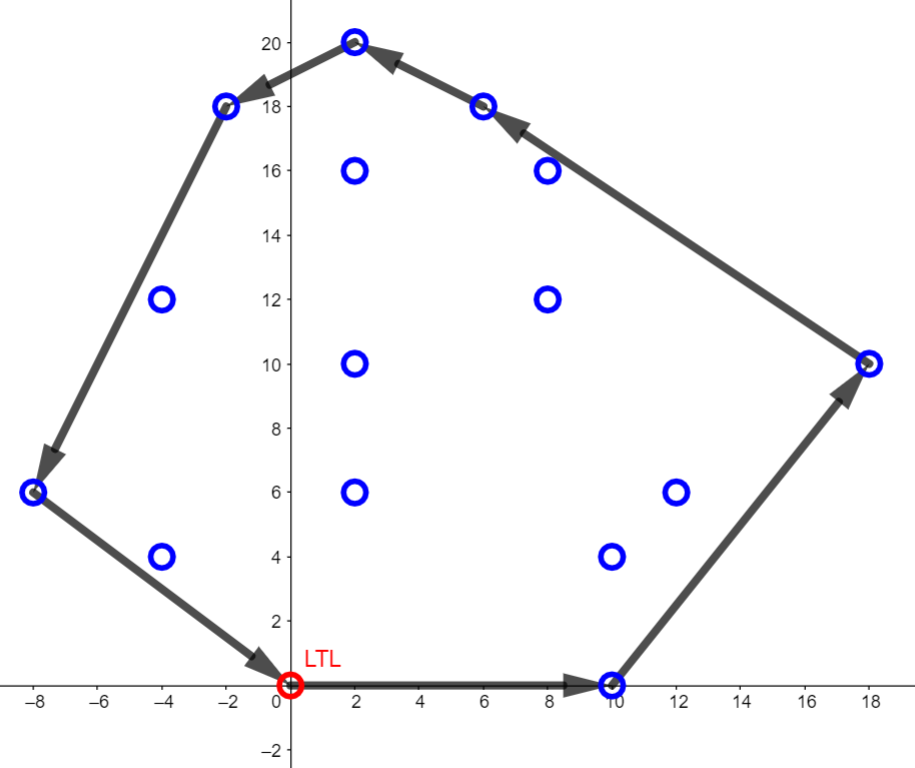
求凸包
struct Vec{
//...
inline bool operator < (Vec b){return fabs(y-b.y) <= EPS ? x < b.x : y < b.y;}
}; typedef Vec Pt;
// Unstrict <==> Strict
// !ToLeft(yyy,xxx) ToLeft(xxx,yyy)
// (Unstrict) ConvexHull, return a CCW CH
// Pt on edge won't be considered part of the CH, uses function "cmpltl" and Pt "LTL"
Pt LTL; inline bool cmpltl(Pt a, Pt b){return Para(a=a-LTL,b=b-LTL) ? ~a < ~b : ToLeft(b,a);}
void CH(Pt p[], int m, Poly &R){
R.clear(), LTL = *min_element(p+1,p+m+1), sort(p+1,p+m+1,cmpltl);
for(rint i = 1; i <= m; R.push(p[i++]))
for(; R.n>1 && !ToLeft(p[i]-R[R.n-1],R[R.n]-R[R.n-1]); R.pop());
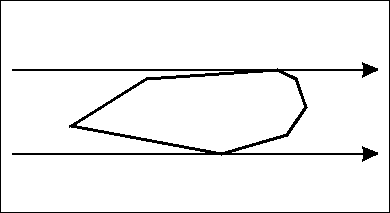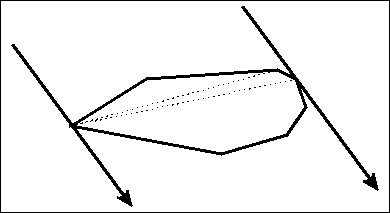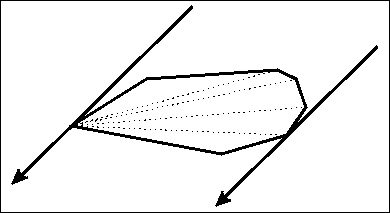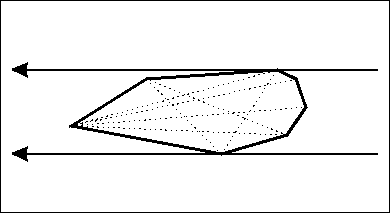
}旋转卡壳
db RC(Poly &R, db Ans=0){
for(rint i = (R[R.n+1] = R[1], 1), j = 2; i <= R.n; Ans = max(Ans,~(R[j]-R[i])), i++)
for(; (R[i+1]-R[i])%(R[j]-R[i]) < (R[i+1]-R[i])%(R[j+1]-R[i]); j = j%R.n+1); return sqrt(Ans);
}
Minkowski和
// Notice that the indices are 0-based
void Minkowski(Poly &A, Poly &B, Poly &R){
rint i = 0, j = 0; R.clear(), R.push_back(A[0]+B[0]);
for(; ;){
p = ToLeft(A[-~i%A.size()]-A[i],B[-~j%B.size()]-B[j]) ?
A[i]+B[++j%=B.size()]
:
A[++i%=A.size()]+B[j];
R.size()>1&&Para(p-R.back(),R.back()-R[R.size()-2]) ?
R.pop_back(),0 : 0;
R.push_back(p); if(!i&&!j) break;
} R.pop_back();
}注意求Minkowski和之前要进行标准化
rotate(p+1,min_element(p+1,p+n+1),p+n+1);另外,严格来说,求出的并非Minkowski和(其是一个有无限个点的集合),而是Minkowski和的凸包。
点与多边形位置关系
单组查询:可能为凹多边形
// Angle ∠AKB
inline db Angle(Pt A, Pt B, Pt K){
static db _; B = B-K, A = A-K, _ = atan2(B.y,B.x)-atan2(A.y,A.x),
_<=-PI-EPS?_+=2*PI:0, _>=PI+EPS?_-=2*PI:0; return _;
}
inline db SumAngle(Poly &R, Pt p){
static db _; _ = 0;
for(rint i = 0; i < R.size(); _ += Angle(R[i],R[-~i%n],p), i++);
return _;
}
// ...
puts(fabs(SumAngle(R,p))>=EPS?"Yes":"No"));点与多边形位置关系
// Pt on edge would be considered part of the CH
bool Q(Poly &E, Pt p){
int _ = lower_bound(E.begin(),E.end()-1,p,cmpltl)-E.begin();
return !ToLeft(E[_]-E[~-_],p-E[~-_]);
}
// ...
puts(LTL==p||(LTL<p&&Q(R,p))?"Yes":"No"));多组查询
注意凸包结尾追加了LTL来避免边界情况
半平面交
inline bool cmpang(Vec a, Vec b){return a.Quad()^b.Quad() ? a.Quad() < b.Quad() : ToLeft(b,a);}
inline bool operator < (Line a, Line b){
return Para(a.v(),b.v()) && a.v()*b.v() > EPS ? ToLeft(a[0]-b[0],b.v()) : cmpang(a.v(),b.v());
}
// ...
// (StrictLeft) HalfPlaneIntersection, return a CCW CH
// L[] should be sorted (with Line's operator < ) before passing in
void HPI(Line L[], int m, Poly &R){
static Line q[MAXN+5]; static int head, tail; R.clear(), head = 1, q[tail=1] = L[1];
for(rint i = 2; i <= m; i++){
if(!cmpang(q[tail].v(),L[i].v())) continue;
for(; head<tail && ToLeft(L[i].v(),Cross(q[tail-1],q[tail])-L[i][0]); --tail);
for(; head<tail && ToLeft(L[i].v(),Cross(q[head+1],q[head])-L[i][0]); ++head);
q[++tail] = L[i];
}
for(; head<tail && ToLeft(q[head].v(),Cross(q[tail-1],q[tail])-q[head][0]); --tail);
for(; head<tail && ToLeft(q[tail].v(),Cross(q[head+1],q[head])-q[tail][0]); ++head);
q[tail+1] = q[head]; for(rint i = head; i <= tail; R.push(Cross(q[i],q[i+1])), i++);
}KD树
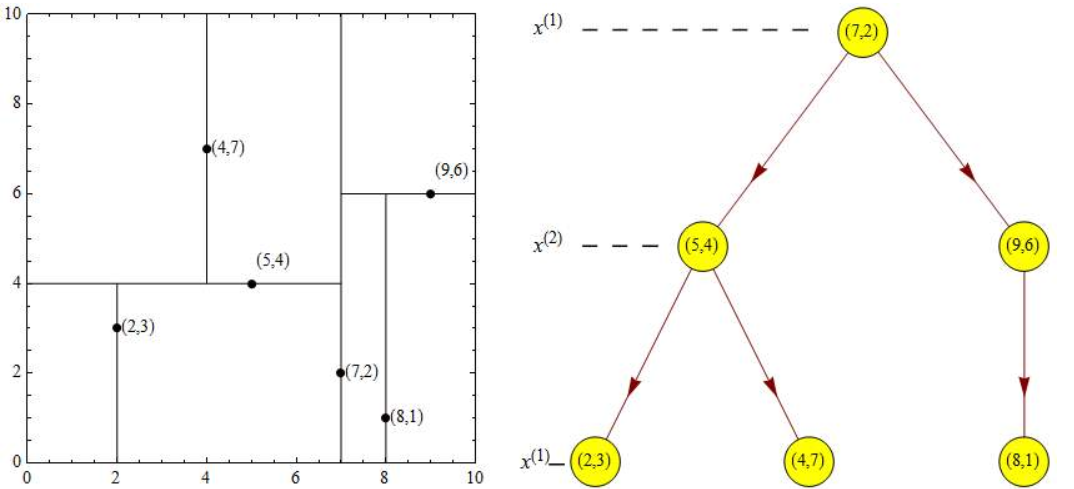
KD树
#define f(x,c) t[x].c
#define lc(x) t[x].c[0]
#define rc(x) t[x].c[1]
#define c(x,y) t[x].c[y]
struct O{int x[2];}dat[MAXN+5];
struct Node{int l, d, r, u, c[2];}t[MAXN+5]; bool kd; int n, rt, mn, mx, ans;
#define dis(a,b) (abs(a.x[0]-b.x[0])+abs(a.x[1]-b.x[1])) // Manhattan Distance
inline bool cmp(O a, O b){return a.x[kd]-b.x[kd] ? a.x[kd]<b.x[kd] : a.x[!kd]<b.x[!kd];}
inline void Push(int p){
for(rint k = 0; k < 2; k++) if(c(p,k))
f(p,l) = min(f(p,l),f(c(p,k),l)), f(p,d) = min(f(p,d),f(c(p,k),d)),
f(p,r) = max(f(p,r),f(c(p,k),r)), f(p,u) = max(f(p,u),f(c(p,k),u));
}
inline int Build(int lef, int rig, int dep){
if(lef > rig) return 0; int mid = lef+rig>>1;
kd = dep&1, nth_element(dat+lef,dat+mid,dat+rig+1,cmp);
lc(mid) = Build(lef,mid-1,dep+1), rc(mid) = Build(mid+1,rig,dep+1);
f(mid,l) = f(mid,r) = dat[mid].x[0], f(mid,d) = f(mid,u) = dat[mid].x[1]; Push(mid); return mid;
}
inline int Maxdis(int p, O a){
return max(abs(a.x[0]-f(p,l)),abs(a.x[0]-f(p,r)))+max(abs(a.x[1]-f(p,d)),abs(a.x[1]-f(p,u)));
}
inline int Mindis(int p, O a){
return max(f(p,l)-a.x[0],0)+max(a.x[0]-f(p,r),0)+max(f(p,d)-a.x[1],0)+max(a.x[1]-f(p,u),0);
}
inline void QMax(int p, O a){
if(!p) return; mx = max(mx,dis(dat[p],a));
int lv = Maxdis(lc(p),a), rv = Maxdis(rc(p),a);
if(lv > rv) lv > mx ? QMax(lc(p),a),0 : 0, rv > mx ? QMax(rc(p),a),0 : 0;
else rv > mx ? QMax(rc(p),a),0 : 0, lv > mx ? QMax(lc(p),a),0 : 0;
}2D树(曼哈顿距离)
KD树
struct O{int x[5];}dat[MAXN+5], o; struct Node{int c[2];}t[MAXN+5];
typedef pair<int,int> pii; priority_queue<pii> q; int K, rt, kd;
inline int dis2(O a, O b, rint ans=0){
for(rint d = 0; d < K; ans += sqr(a.x[d]-b.x[d]), d++); return ans;
}
inline bool cmp(O a, O b){return a.x[kd]-b.x[kd] ? a.x[kd]<b.x[kd] : a.x[!kd]<b.x[!kd];}
inline int Build(int lef, int rig, int dep){
if(lef > rig) return 0; int mid = lef+rig>>1;
kd = dep%K, nth_element(dat+lef,dat+mid,dat+rig+1,cmp);
lc(mid) = Build(lef,mid-1,dep+1), rc(mid) = Build(mid+1,rig,dep+1); return mid;
}
inline void Query(int p, O &a, int dep){
if(!p) return; kd = dep%K; int v = dis2(dat[p],a), r = cmp(dat[p],a); Query(c(p,r),a,dep+1);
if(q.size()<M) q.push(pii(v,p)); else if(v<q.top().first) q.pop(), q.push(pii(v,p));
kd = dep%K; if(q.size()<M||sqr(dat[p].x[kd]-a.x[kd])<q.top().first) Query(c(p,!r),a,dep+1);
}KD树(欧几里得距离)
没有什么卵用但是加上总比不加要好的KD树各种剪枝优化.jpg
进阶(2D)解析几何
圆的(外)公切线
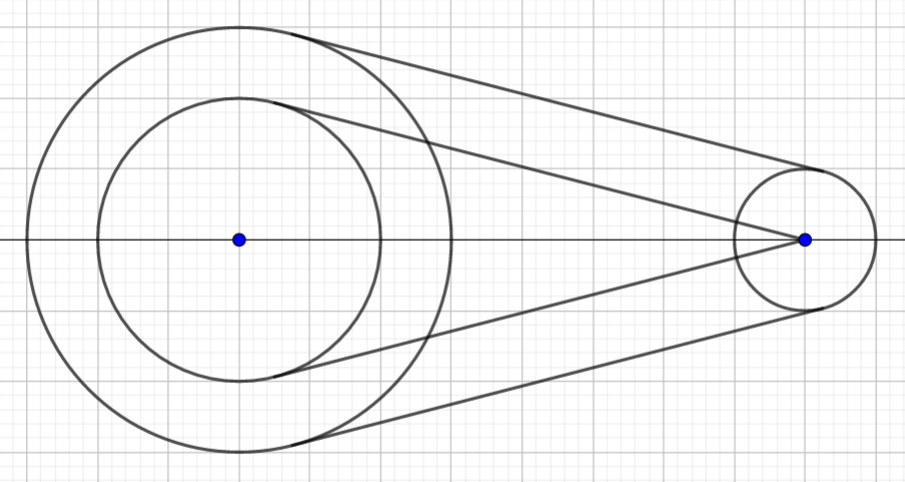
圆反演
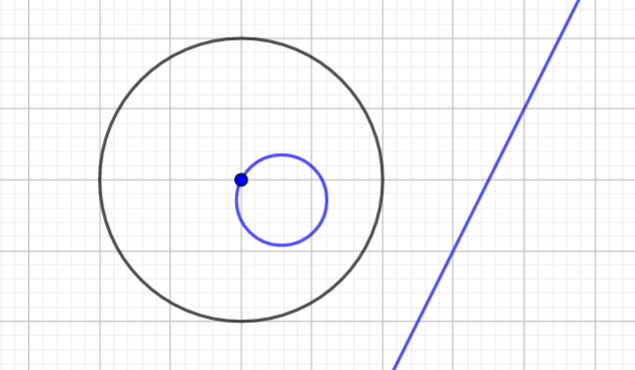
反演是可逆双射
不过反演中心的直线
过反演中心的圆
不过反演中心的圆
不过反演中心的圆
(且半径之比等于到反演圆心距离之比)
反演不改变相切性
(自适应)辛普森积分
inline db Integ(db l, db r){
static db m; m = (l+r)/2;
return (r-l)/6*(F(l)+4*F(m)+F(r));
}
inline db Simpson(db l, db r, db S){
db m = (l+r)/2, a = Integ(l,m), b = Integ(m,r);
return fabs(a+b-S)<=EPS ? S+(a+b-S)/15 : Simpson(l,m,a)+Simpson(m,r,b);
}(自适应)辛普森积分
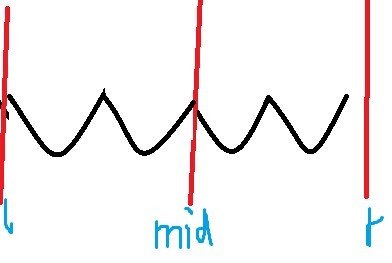
(第一次手动随机划分子区间/区间端点做微小扰动)
(3D)计算几何
混合积
空间体体积
a,b,c三个向量构成的平行六面体有向体积为
若a,b,c构成右手系则有向体积为正, 左手系则有向体积为负
空间向量方向
空间平面法向量
b,c两个向量确定的平面法向量为
空间三角形面积
或海伦公式
Fun Problem Time!
题目顺序是随机的
POJ 2242
求三角形外接圆周长
POJ 2242
正弦定理:
BZOJ 1502
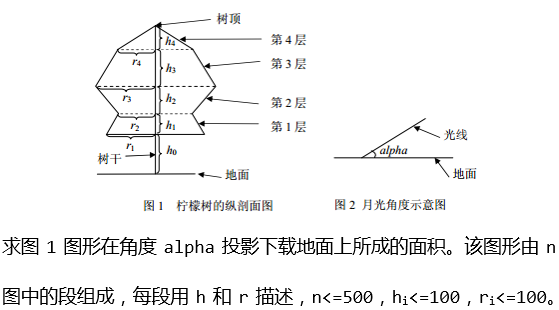
BZOJ 1502

投影后圆心的位置:
BZOJ 1502

投影后圆心的位置:
投影后圆半径不变
BZOJ 1502

投影后圆心的位置:
投影后圆半径不变
求出公切线后整个函数图像就确定了,要求函数面积
BZOJ 1502

投影后圆心的位置:
投影后圆半径不变
求出公切线后整个函数图像就确定了,要求函数面积
BZOJ 5317
BZOJ 5317
题目等价于:
BZOJ 5317
题目等价于:
BZOJ 5317
题目等价于:
Minkowski和
BZOJ 5317
题目等价于:
Minkowski和
判断一个点位置?
BZOJ 5317
题目等价于:
Minkowski和
判断一个点位置?
极角排序+二分
POJ 3301
正方形旋转角度未知,但是具有周期性
POJ 3301
在一个周期内答案是单峰的
三分枚举旋转角即可
\(n\)特别小,可以随便乱搞
UOJ 326
显然只有在极角\(OP_i\)到\(OP_j\)范围内的点是有用的
UOJ 326
显然只有在极角\(OP_i\)到\(OP_j\)范围内的点是有用的
UOJ 326
进一步,只需要记录极角序最小的即可
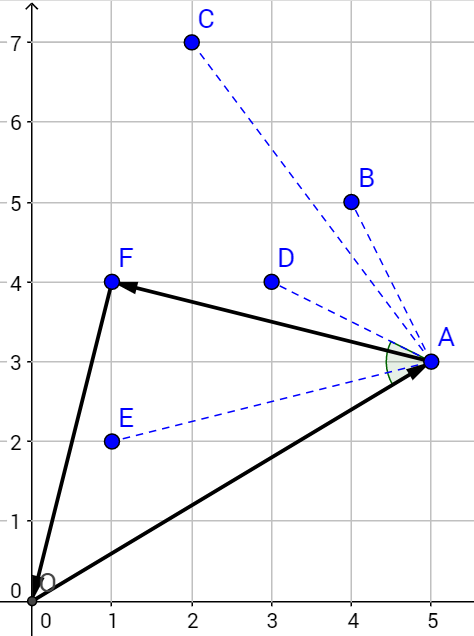
Codeforces 889D
要求投影点到某直线投影关于一点中心对称,即所有点关于直线的垂线中心对称。
Codeforces 889D
要求投影点到某直线投影关于一点中心对称,即所有点关于直线的垂线中心对称。
Codeforces 889D
要求投影点到某直线投影关于一点中心对称,即所有点关于直线的垂线中心对称。
因此答案一定过某两点的中点。
两点确定一条直线。\(O(n^5 \log n)\)
Codeforces 889D
注意到在旋转后目标直线一定满足\(\sum x_i=\sum y_i=0\)
而旋转本身不影响加和的比例,故目标直线一定过整个点集的重心。
只需要枚举一个中点加上重心即可。\(O(n^3 \log n)\)
Codeforces 889D
注意到每个点都要配对,只需要考虑一号点的匹配对象
枚举一号点的匹配,加上重心。\(O(n^2 \log n)\)
等价于判断是否整个回路上所有点都严格在大圆的同一侧。
等价于判断是否整个回路上所有点都严格在大圆的同一侧。
对于一个确定的大圆,枚举每个点,三维混合积判断即可。
枚举大圆?
等价于判断是否整个回路上所有点都严格在大圆的同一侧。
对于一个确定的大圆,枚举每个点,三维混合积判断即可。
枚举大圆?
枚举两个点,其与圆心确定的平面作为大圆的可能选择
等价于判断是否整个回路上所有点都严格在大圆的同一侧。
对于一个确定的大圆,枚举每个点,三维混合积判断即可。
枚举大圆?
枚举两个点,其与圆心确定的平面作为大圆的可能选择
random_shuffle(p+1,p+n+1)等价于判断是否整个回路上所有点都严格在大圆的同一侧。
对于一个确定的大圆,枚举每个点,三维混合积判断即可。
枚举大圆?
枚举两个点,其与圆心确定的平面作为大圆的可能选择
random_shuffle(p+1,p+n+1)接触也合法,可以把大圆沿法向量翻转一个小角度
TopCoder 10308
考虑贡献法
TopCoder 10308
考虑贡献法
TopCoder 10308
考虑贡献法
TopCoder 10308
枚举点和 做中垂线,所有中垂线靠近 一侧的半平面交就是所有最远点是 的点的集合。
考虑贡献法
TopCoder 10308
枚举点和 做中垂线,所有中垂线靠近 一侧的半平面交就是所有最远点是 的点的集合。
然后算出经过 的角度,再和 边界取交即可
TopCoder 10308
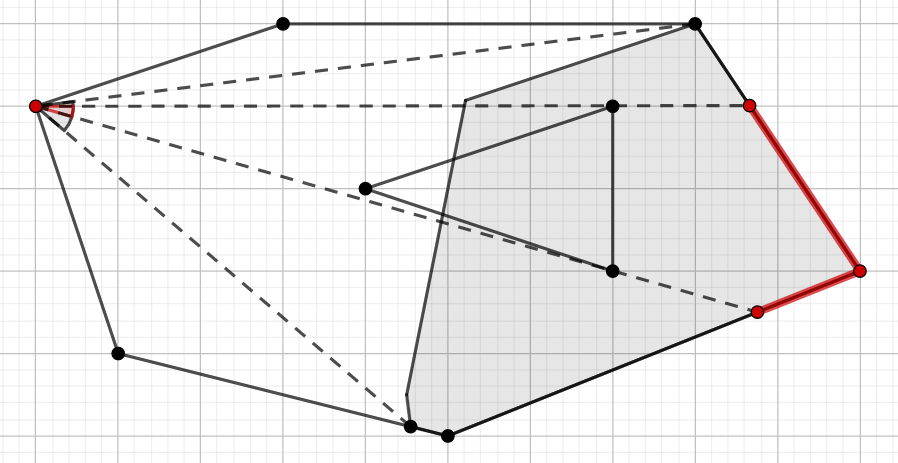
ZROJ 76
二分答案(第二近邻距离),那么答案点必然在圆弧上
ZROJ 76
二分答案(第二近邻距离),那么答案点必然在圆弧上
ZROJ 76
这个点是第二近邻,当且仅当其在另一个圆内(或圆上)
二分答案(第二近邻距离),那么答案点必然在圆弧上
ZROJ 76
这个点是第二近邻,当且仅当其在另一个圆内(或圆上)
也就是判断是否存在一段圆弧是否被其他圆覆盖恰好一次
二分答案(第二近邻距离),那么答案点必然在圆弧上
ZROJ 76
这个点是第二近邻,当且仅当其在另一个圆内(或圆上)
也就是判断是否存在一段圆弧是否被其他圆覆盖恰好一次
圆求交、圆弧求交(由于等半径,所以圆求交很好做)
二分答案(第二近邻距离),那么答案点必然在圆弧上
ZROJ 76
这个点是第二近邻,当且仅当其在另一个圆内(或圆上)
也就是判断是否存在一段圆弧是否被其他圆覆盖恰好一次
圆求交、圆弧求交(由于等半径,所以圆求交很好做)
事实上小于等于一次即可,如果一个点是最近邻,第二近邻一定更远
注意圆还要和矩形边界求交
BZOJ 1069
显然这四个点都在凸包上
BZOJ 1069
显然这四个点都在凸包上
BZOJ 1069
枚举对角线上两个点,两侧都要求面积最大的三角形
显然这四个点都在凸包上
BZOJ 1069
枚举对角线上两个点,两侧都要求面积最大的三角形
枚举左端点,一边枚举右端点一边旋转卡壳
BZOJ 1069
db RC(Polygon &R, db Ans=0){
for(rint l = (R[R.n+1] = R[1], 1), r, i, j; l <= R.n; l++)
for(i = l%R.n+1, r = l+2, j = r%R.n+1; r <= R.n; r++){
for(; i%R.n+1!=r && (R[i]-R[l])%(R[r]-R[l]) < (R[i+1]-R[l])%(R[r]-R[l]); i = i%R.n+1);
for(; j%R.n+1!=l && (R[j]-R[r])%(R[l]-R[r]) < (R[j+1]-R[r])%(R[l]-R[r]); j = j%R.n+1);
Ans = max(Ans,(R[i]-R[l])%(R[r]-R[l])+(R[j]-R[r])%(R[l]-R[r]));
} return Ans/2.;
}HDU 4773
当然只能是圆反演了
HDU 4773
当然只能是圆反演了
HDU 4773
对点O做反演,原来的两个圆都会边长位似圆,现在要求的答案也就是外公切线了。
当然只能是圆反演了
HDU 4773
对点O做反演,原来的两个圆都会边长位似圆,现在要求的答案也就是外公切线了。
怎么判断外公切线和内公切线?
当然只能是圆反演了
HDU 4773
对点O做反演,原来的两个圆都会边长位似圆,现在要求的答案也就是外公切线了。
怎么判断外公切线和内公切线?
其实本来就是只有外公切线
Codeforces 975E
只需要维护重心以及重心到每个点的向量即可。每次重力作用相当于是将某个重心到点的向量旋转为竖直向上。
Codeforces 975E
向量旋转
计算角度
多边形重心
只需要维护重心以及重心到每个点的向量即可。每次重力作用相当于是将某个重心到点的向量旋转为竖直向上。
Codeforces 975E
向量旋转
计算角度
多边形重心
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
BZOJ 2732
BZOJ 2732
考虑线段(x,[l,r]):
BZOJ 2732
考虑线段(x,[l,r]):
(a,b)点集的半平面交
ZROJ 144
ZROJ 144
三角形重心
ZROJ 144
三角形重心
ZROJ 144
三角形重心
Minkowski和
ZROJ 144
三角形重心
Minkowski和
判断一个点位置?
极角排序+二分
(似曾相识)
BZOJ 1100
Mix
BZOJ 1100
Mix
将一个多边形哈希成一个字符串(例如「叉积+边长」序列)
BZOJ 1100
Mix
将一个多边形哈希成一个字符串(例如「叉积+边长」序列)
轴对称
倍长串的最长回文子串长度
SGU 198
Mix
SGU 198
Mix
可以将这个圆的半径加到其他圆上,这个圆变为一个点。
SGU 198
Mix
可以将这个圆的半径加到其他圆上,这个圆变为一个点。
相交的圆之间连一条边,问题就是是否存在一个闭合区域(多边形)包含了当前点。
SGU 198
Mix
可以将这个圆的半径加到其他圆上,这个圆变为一个点。
相交的圆之间连一条边,问题就是是否存在一个闭合区域(多边形)包含了当前点。
如果点在多边形内和为2π或-2π,否则和为0。那么问题就相当于求是否所有环的有向夹角和都为0。
SGU 198
Mix
可以将这个圆的半径加到其他圆上,这个圆变为一个点。
相交的圆之间连一条边,问题就是是否存在一个闭合区域(多边形)包含了当前点。
如果点在多边形内和为2π或-2π,否则和为0。那么问题就相当于求是否所有环的有向夹角和都为0。
注意到对于一对反向的边,其有向夹角相反,存在和为X的环就一定存在和为-X的环。问题就转化为求是否有负环。
SGU 198
Mix
可以将这个圆的半径加到其他圆上,这个圆变为一个点。
相交的圆之间连一条边,问题就是是否存在一个闭合区域(多边形)包含了当前点。
如果点在多边形内和为2π或-2π,否则和为0。那么问题就相当于求是否所有环的有向夹角和都为0。
注意到对于一对反向的边,其有向夹角相反,存在和为X的环就一定存在和为-X的环。问题就转化为求是否有负环。
SPFA判负环
Codeforces 704E
Mix
Codeforces 704E
Mix
考虑链上问题,将时间看成x轴,下标看成y轴,所求的是最左侧的线段交点。
Codeforces 704E
Mix
考虑链上问题,将时间看成x轴,下标看成y轴,所求的是最左侧的线段交点。
这有一个神奇的特点: 在发现这个交点之前,线段是无交的。换言之,是存在良序定义的。
Codeforces 704E
Mix
考虑链上问题,将时间看成x轴,下标看成y轴,所求的是最左侧的线段交点。
这有一个神奇的特点: 在发现这个交点之前,线段是无交的。换言之,是存在良序定义的。
用 维护。
std::setCodeforces 704E
Mix
考虑链上问题,将时间看成x轴,下标看成y轴,所求的是最左侧的线段交点。
这有一个神奇的特点: 在发现这个交点之前,线段是无交的。换言之,是存在良序定义的。
用 维护。
std::set树上问题?
Codeforces 704E
Mix
考虑链上问题,将时间看成x轴,下标看成y轴,所求的是最左侧的线段交点。
这有一个神奇的特点: 在发现这个交点之前,线段是无交的。换言之,是存在良序定义的。
用 维护。
std::set树上问题?
树链剖分,把所有线段分解到DFS序区间上
BZOJ 2391
Mix
三角剖分
BZOJ 2391
Mix
三角剖分
BZOJ 2391
每个小三角形怎么统计点数?
Mix
三角剖分
BZOJ 2391
每个小三角形怎么统计点数?
类似于Range Tree的思想,不过是暴力Range Tree
Mix
UOJ 326 ++
三角剖分
BZOJ 2391
每个小三角形怎么统计点数?
类似于Range Tree的思想,不过是暴力Range Tree
n棵平衡树
Mix
UOJ 326 ++
BZOJ 5316
Mix
BZOJ 5316
Mix
二分答案,然后求出每个点能到达的圆的圆弧(的辐角区间),然后枚举角度看是否存在二分图完备匹配即可。
枚举角度?
BZOJ 5316
Mix
二分答案,然后求出每个点能到达的圆的圆弧(的辐角区间),然后枚举角度看是否存在二分图完备匹配即可。
枚举角度?
一定存在一种方案使得某个点卡在端点上。因此只有 个旋转角。
BZOJ 5316
Mix
二分答案,然后求出每个点能到达的圆的圆弧(的辐角区间),然后枚举角度看是否存在二分图完备匹配即可。
枚举角度?
一定存在一种方案使得某个点卡在端点上。因此只有 个旋转角。
二分图匹配Dinic复杂度 ,总复杂度约为
BZOJ 5316
Mix
二分答案,然后求出每个点能到达的圆的圆弧(的辐角区间),然后枚举角度看是否存在二分图完备匹配即可。
网络流退流
一定存在一种方案使得某个点卡在端点上。因此只有 个旋转角。
二分图匹配Dinic复杂度 ,总复杂度约为
枚举角度?
BZOJ 5328
Mix

Mix
旋转一下
BZOJ 5328
Mix
旋转一下
BZOJ 5328
扫描线
Mix
旋转一下
BZOJ 5328
然后李超树随便一个什么数据结构维护一下就可以了
扫描线
Mix
旋转一下
BZOJ 5328
然后李超树随便一个什么数据结构维护一下就可以了
扫描线
(推荐手写尝试)
SGU 303
Mix
SGU 303
Mix
实际上就是在求平面图最小割
SGU 303
Mix
实际上就是在求平面图最小割
= 对偶图最短路
SGU 303
Mix
实际上就是在求平面图最小割
= 对偶图最短路
最小左转法建对偶图
THUWC 2019 D2T3
Mix
Mix
THUWC 2019 D2T3
凸多边形面积当然是要拆开每条边算了(经典操作)
Mix
THUWC 2019 D2T3
凸多边形面积当然是要拆开每条边算了(经典操作)
方差当然也是要拆开了(经典操作)
(即:方差 = 平方的期望 - 期望的平方)
Mix
THUWC 2019 D2T3
于是只需要维护方案数(0次方期望),面积(1次方期望),面积平方和(2次方期望)即可。
Mix
THUWC 2019 D2T3
于是只需要维护方案数(0次方期望),面积(1次方期望),面积平方和(2次方期望)即可。
Mix
THUWC 2019 D2T3
于是只需要维护方案数(0次方期望),面积(1次方期望),面积平方和(2次方期望)即可。
注意到(b,c)和(c,d)需要满足极角序单调关系,可以前缀和优化。
Mix
Mix
三角剖分
Mix
三角剖分
考虑将旋转多边形,改为旋转点集
Mix
三角剖分
考虑将旋转多边形,改为旋转点集
就是圆和三角形求交
Mix
三角剖分
考虑将旋转多边形,改为旋转点集
就是圆和三角形求交
圆线求交与圆弧交
Mix
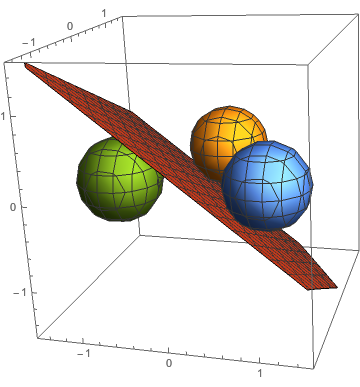
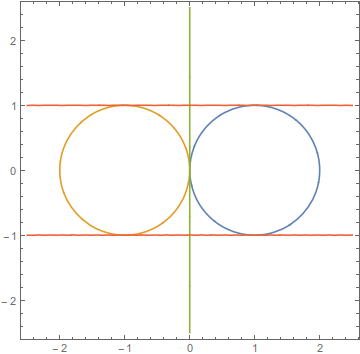
Mix
点到直线距离公式·高维版
Mix
点到直线距离公式·高维版
高斯消元
Mix
点到直线距离公式·高维版
高斯消元
n个方程,n+1个变量?
Mix
点到直线距离公式·高维版
高斯消元
n个方程,n+1个变量?
其实无所谓,设成是个定值
Thank You
