Double-bracket quantum algorithms for diagonalization
Marek Gluza
NTU Singapore
slides.com/marekgluza

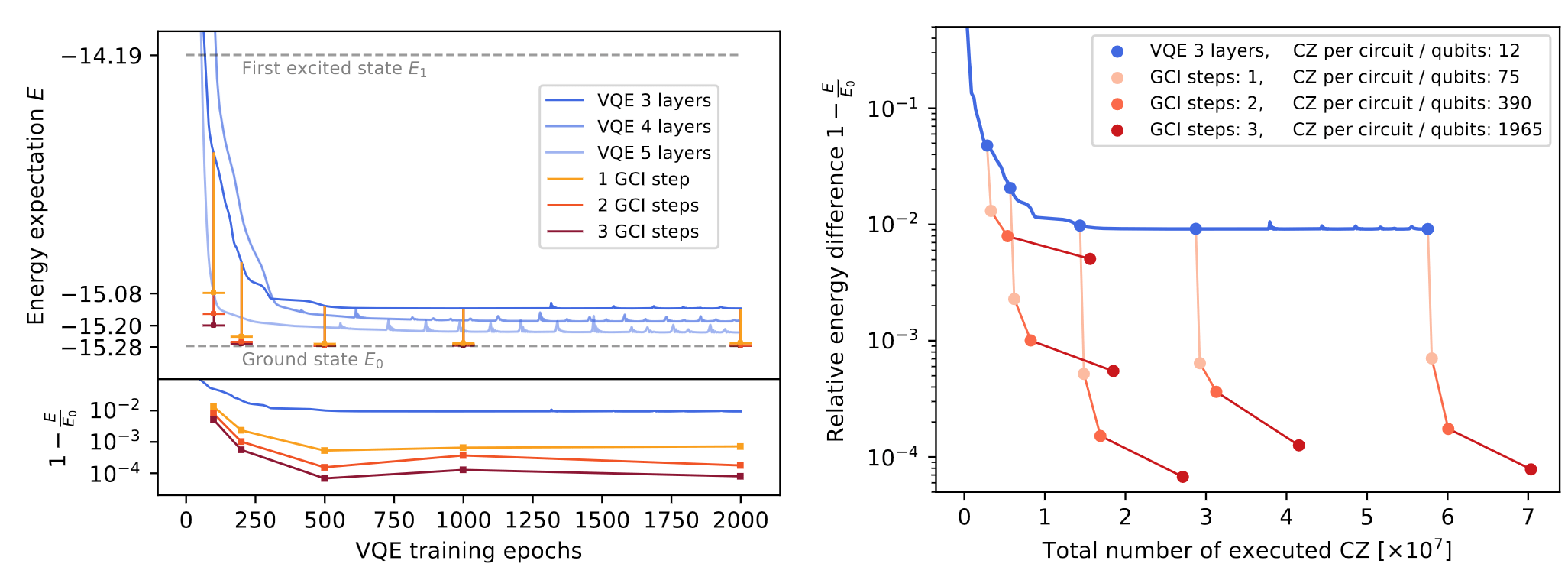
Gate count after VQE warm-start:
Why double a bracket?
Why double a bracket?
2 qubit unitary
Canonical
Double-bracket quantum algorithms
are inspired by double-bracket flows
and allow for quantum compiling of short-depth circuits which approximate grounds states
Inspired by double-bracket flows we compiled quantum circuits which yield quantum states relevant for material science

2 qubit unitary
Canonical
Double-bracket rotation ansatz
antihermitian
Rotation generator:
Input:
Unitary rotation:
Double-bracket rotation:
Double-bracket rotation ansatz
Rotation generator:
Input:
Unitary rotation:
Double-bracket rotation:
Key point: If \(\hat D_0\) is diagonal then
\(\hat H_1\) should be "more" diagonal than \(\hat H_0\)
Double-bracket rotation ansatz
Rotation generator:
Input:
Double-bracket rotation:
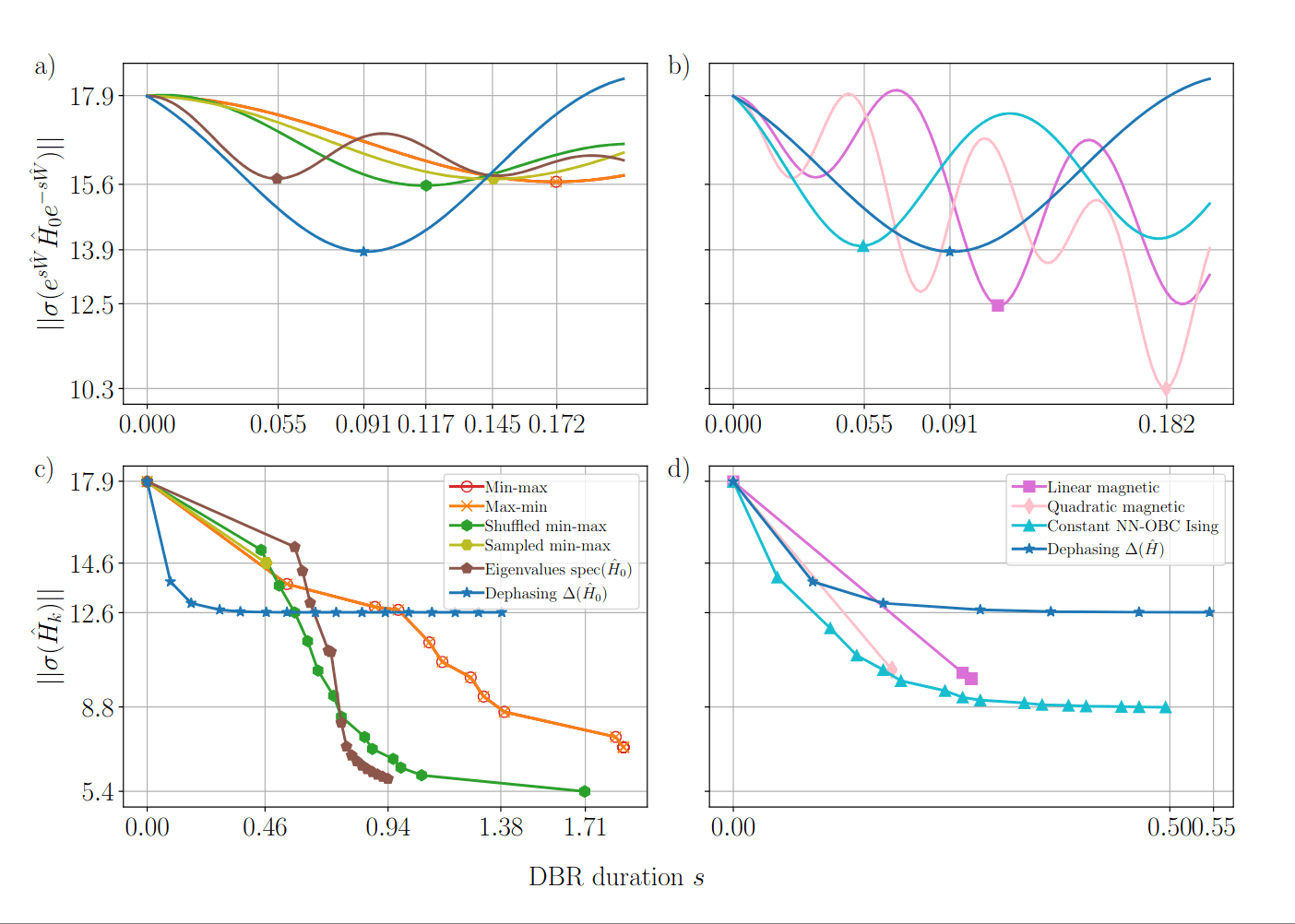
Restriction to off-diagonal
Lemma:
Proof: Taylor expand, shuffle around (fun!)
Double-bracket rotation ansatz
Rotation generator:
Input:
Double-bracket rotation:
Restriction to off-diagonal
Lemma:
Proof: Taylor expand, shuffle around (fun!)
A new approach to diagonalization on a quantum computer

Double-bracket iteration


Głazek-Wilson-Wegner flow
Restriction to off-diagonal
Restriction to diagonal
as a quantum algorithm
(addendo: where it's coming from)
Głazek-Wilson-Wegner flow
as a quantum algorithm
(addendo: where it's coming from)
New quantum algorithm for diagonalization
0
0
0
0

1) Dephasing
2) Group commutator
3) Frame shifting

Fun but painful because probably not possible efficiently
What about other methods?
0
0
0
0
Universal gate set:
single qubit rotations + generic 2 qubit gate
Universal gate set can approximate any unitary
What is a universal quantum computer?
quantum compiling approximates unitaries with circuits
Quantum compiling
2x2 unitary matrix - use Euler angles
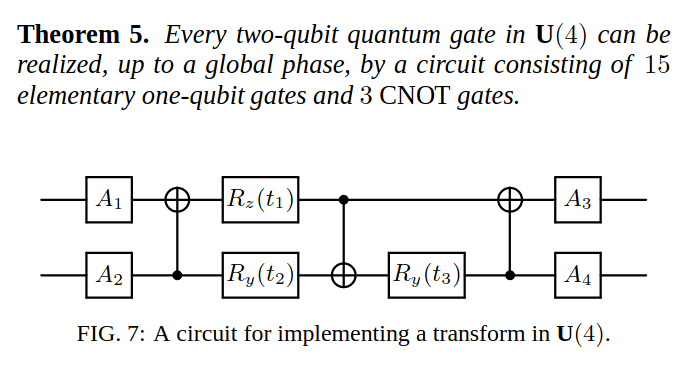
4x4 unitary matrix - use KAK decomposition + 3x CNOT formula
2 qubit unitary
Canonical
KAK decomposition, Brockett's work etc
=
2 qubit unitaries modulo single qubit unitaries are a 3 dimensional torus
Quantum compiling
\(2\) qubits - \(4\times 4\) unitary matrix - use KAK decomposition + \(3\) CNOT formula

Quantum compiling
\(1\) qubit - \(2\times 2\) unitary matrix - use Euler angles
\(n\) qubits - \(2^n\) unitary matrix - use quantum Shannon decomposition + \(O(4^n)\) CNOT formula
Variational quantum eigensolver
0
0
0
0
+
+
+
+
+
This works but is inefficient
This is efficient but doesn't work
Open: fill this gap!
Double-bracket iteration
Rotation durations:
Input:
Diagonal generators:
A new approach to diagonalization on a quantum computer
Great: we can diagonalize
How to quantum compile?
How to quantum?
Group commutator
0
0
0
0

Want
New bound
Group commutator during iteration
0
0
0
0

Group commutator during iteration
0
0
0
0

Double-bracket iteration
Rotation durations:
Input:
Diagonal generators:
A new approach to diagonalization on a quantum computer
Great: we can diagonalize
How to quantum compile?
Replace by the group commutator
Group commutator iteration
Double-bracket iteration
Double-bracket iteration
Transition from theory to QPUs
How well does it work?

Variational flow example
Notice the steady increase of diagonal dominance.


Variational vs. GWW flow


Notice that degeneracies limit GWW diagonalization but variational brackets can lift them.

GWW for 9 qubits
Notice the spectrum is almost converged.



GWW for 9 qubits
Notice that some of them are essentially eigenstates!
How does it work after warm-start?
10 qubit, 50 layers of CNOT - 99.5% ground state fidelity
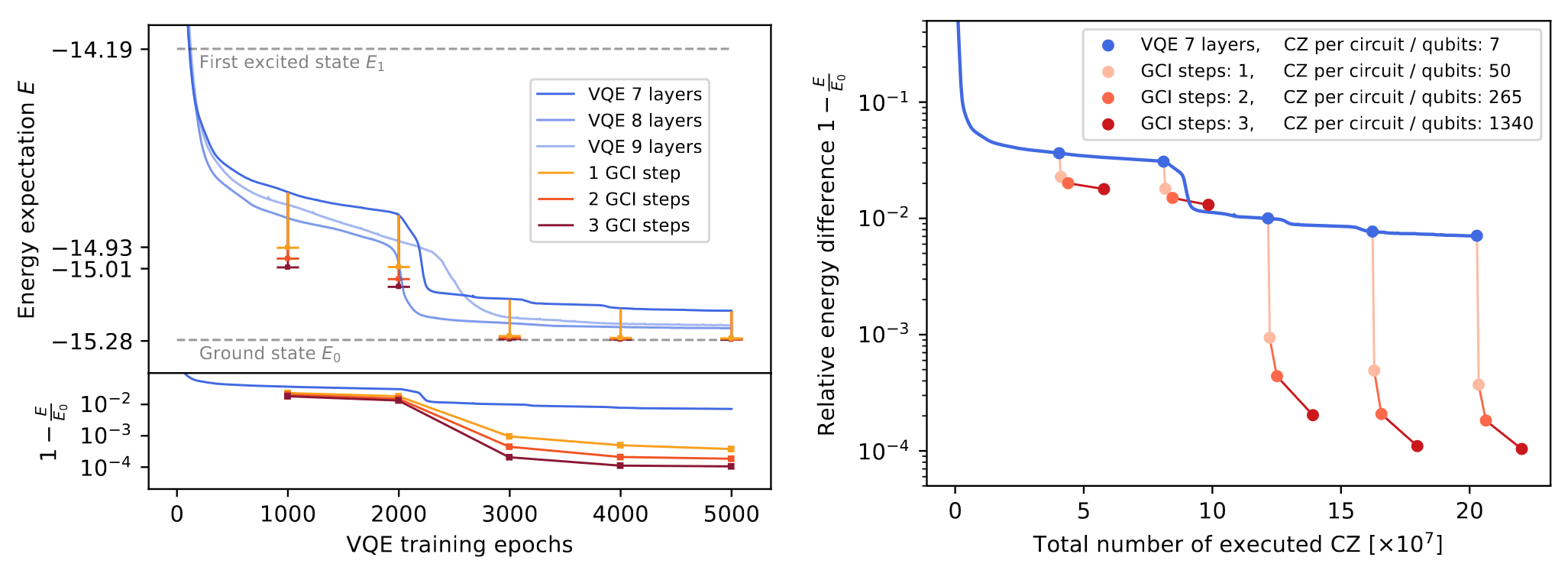
This both works and is efficient
How to interface VQE and DBQA?
Quantum Dynamic Programming


with J. Son, R. Takagi and N. Ng
QDP code structure


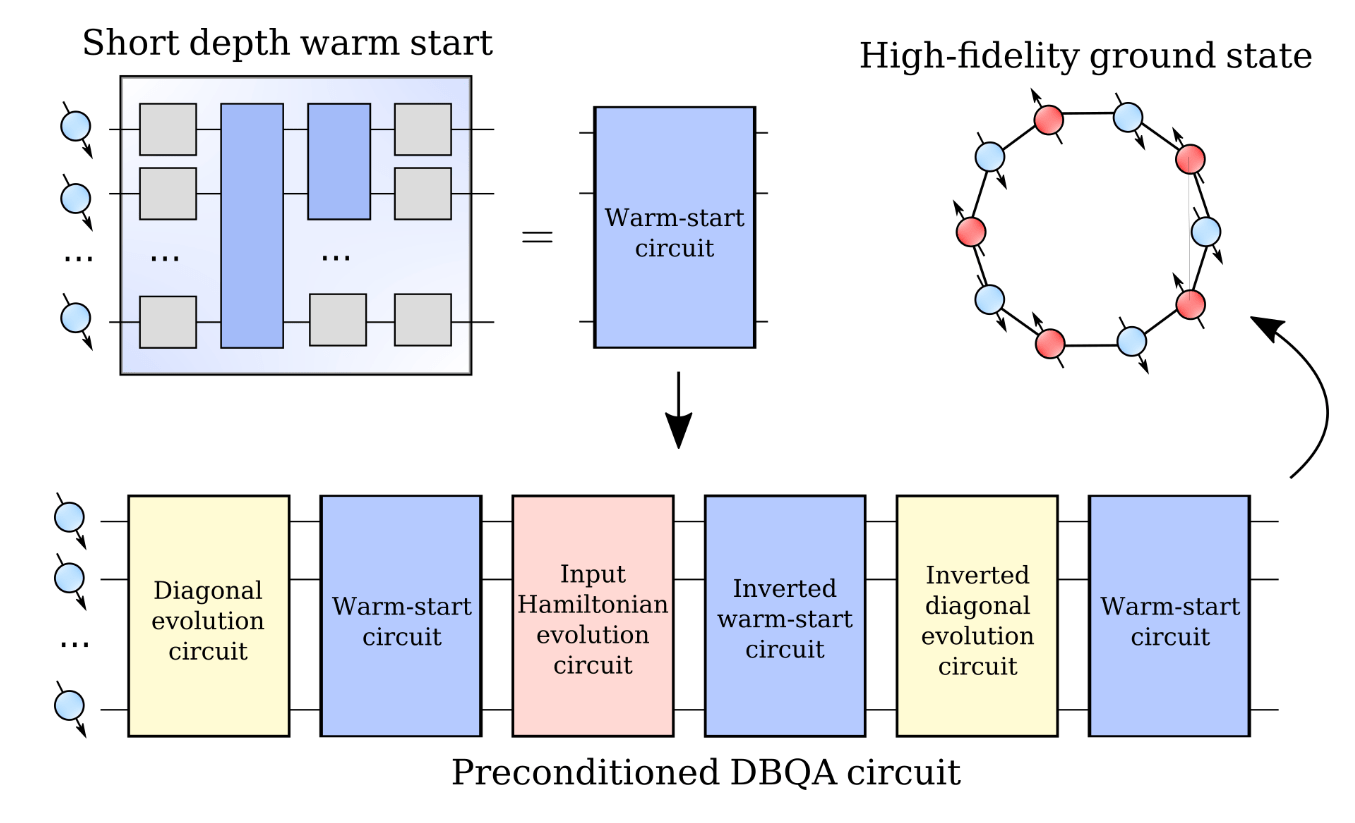
Warm-start unitary from variational quantum eigensolver
0
0
0
0
+
+
+
+
+
DBQA input with warmstart
Use unitarity and get circuit VQE insertions

10 qubit, 50 layers of CNOT - 99.5% ground state fidelity

2 qubit unitary
Canonical
Canonical
For quantum compiling we use:
- higher-order group commutators
- higher-order Trotter-Suzuki decomposition
- 3-CNOT formulas
New quantum algorithm for diagonalization
no qubit overheads
no controlled-unitaries
0
0
0
0
C
0
0
0
0
Simple
=
Easy
Doesn't spark joy :(
Double-bracket quantum algorithm for diagonalization
new approach to preparing useful states
0
0
0
0




What else is there?
Linear programming
Matching optimization
Diagonalization
Sorting
QR decomposition
Toda flow
Double-bracket flow
Runtime-boosting heuristics
Analytical convergence analysis
Group commutator bound
Hasting's conjecture
Relation to other quantum algorithms
Code is available on Github
0
0
0
0
C

Double-bracket quantum algorithms for diagonalization

with J. Son, R. Takagi and N. Ng
Quantum dynamic programming
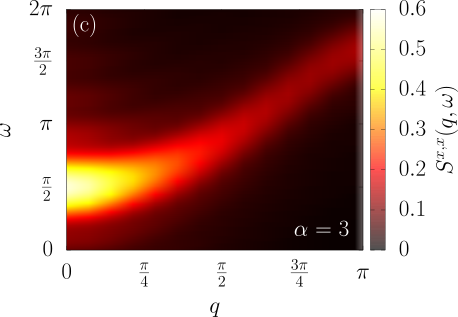
Material science?
0
0
0
0
C


How to dynamically quantum?
Group commutator
0
0
0
0

Want
New bound
Group commutator
0
0
0
0

Want
How to get ?





Phase flip unitaries
N
S
N
S
N
S
N
S











N
S
N
S
N
S
Phase flip unitaries
Evolution under dephased generators
0
0
0
0

We can make it efficient:
Use unitarity
and repeat many times
New quantum algorithm for diagonalization
0
0
0
0

1) Dephasing
2) Group commutator
3) Frame shifting