Double-bracket quantum algorithms for diagonalization
Marek Gluza
NTU Singapore
slides.com/marekgluza
New quantum algorithm for diagonalization
\hat H \mapsto \hat \mathcal H_\ell = \hat \mathcal U_\ell^\dagger \hat H \hat\mathcal U_\ell
\partial_\ell \hat \mathcal H_\ell = [[A(\hat \mathcal H_\ell),B(\hat \mathcal H_\ell)], \hat \mathcal H_\ell]
no qubit overheads
no controlled-unitaries
0
0
0
0
C
0
0
0
0
Simple
=
Easy
Doesn't spark joy :(
New quantum algorithm for diagonalization
\hat H \mapsto \hat H_\ell = \hat U_\ell^\dagger \hat H \hat U_\ell
\partial_\ell \hat H_\ell = [[A(\hat H_\ell),B(\hat H_\ell)], \hat H_\ell]
building useful quantum algorithms
new approach to preparing useful states
building useful variational circuits
tons of fun maths in the appendix
no qubit overheads
no controlled-unitaries
0
0
0
0
Why double a bracket?
\partial_t \hat A(t) = i [ \hat H(t), \hat A(t)]
\partial_t \hat A(t) = [ \hat H(t), [\hat H(t), \hat A(t)]]
\hat H_1 = e^{s_0 \hat W_0} \hat H_0 e^{-s_0 \hat W_0}
\hat W_0
= [\hat D_0,\hat H_0]
Double-bracket rotation ansatz
antihermitian
\left(i\hat H\right)^\dagger = -i \hat H
Rotation generator:
Input:
Unitary rotation:
e^{s \hat W_0}
\hat H_0
Double-bracket rotation:
\partial_s \hat H_0(s) = [\hat W_0, \hat H_0]
\Leftrightarrow
= [[\hat D_0, \hat H_0], \hat H_0(s)]
\hat H_1 = e^{s_0 \hat W_0} \hat H_0 e^{-s_0 \hat W_0}
\hat W_0
= [\hat D_0,\hat H_0]
Double-bracket rotation ansatz
Rotation generator:
Input:
Unitary rotation:
e^{s \hat W_0}
\hat H_0
Double-bracket rotation:
\hat D_0
- diagonal operator
today: how to choose it to diagonalize and not get stuck?
\hat H_1 = e^{s_0 \hat W_0} \hat H_0 e^{-s_0 \hat W_0}
\hat W_0
= [\hat D_0,\hat H_0]
Double-bracket rotation ansatz
Rotation generator:
Input:
Unitary rotation:
e^{s \hat W_0}
\hat H_0
Double-bracket rotation:
\hat H_\text{TFIM} = \sum_{i=1}^{L-1}\hat X_i\hat X_{i+1}+\sum_{i=1}^L \hat Z_i
\hat H(s) = e^{s \hat W_0} \hat H_0 e^{-s \hat W_0}
\hat W_0
= [\hat D_0,\hat H_0]
Double-bracket rotation ansatz
Rotation generator:
Input:
\hat H_0
Double-bracket rotation:
\sigma(\hat H_\ell)
Restriction to off-diagonal
\partial_s \|\sigma(\hat H_0(s))\|_{\text{HS}}^2 = -2\langle \hat W_0,[\hat H_0, \sigma(\hat H_0)]\rangle_{\text{HS}}
Lemma:
Proof: Taylor expand, shuffle around (fun!)
\hat H(s) = e^{s \hat W_0} \hat H_0 e^{-s \hat W_0}
\hat W_0
= [\hat D_0,\hat H_0]
Double-bracket rotation ansatz
Rotation generator:
Input:
\hat H_0
Double-bracket rotation:
\sigma(\hat H_\ell)
Restriction to off-diagonal
\partial_s \|\sigma(\hat H_0(s))\|_{\text{HS}}^2 = -2\langle \hat W_0,[\hat H_0, \sigma(\hat H_0)]\rangle_{\text{HS}}
Lemma:
Proof: Taylor expand, shuffle around (fun!)
A new approach to diagonalization on a quantum computer
\hat H_1 = e^{s \hat W_1} \hat H e^{-s \hat W_1}
\hat W_k = [D_{k-1},\hat H_{k-1}]
\hat H_k = e^{s \hat W_k} \hat H_{k-1} e^{-s \hat W_k}
\hat H_\text{TFIM} = \sum_{i=1}^{L-1}\hat X_i\hat X_{i+1}+\sum_{i=1}^L \hat Z_i
Double-bracket iteration
\hat W_1 = [\hat D_0,\hat H_0]
\partial_\ell \hat H_\ell = [\hat W_\ell, \hat H_\ell]
\hat W_\ell = [\Delta(\hat H_\ell),\sigma(\hat H_\ell)]
\Delta(\hat H_\ell)
\sigma(\hat H_\ell)
Głazek-Wilson-Wegner flow
Restriction to off-diagonal
Restriction to diagonal
\partial_\ell \|\sigma(\hat H_\ell)\|_{\text{HS}}^2 = -2\|\hat W_\ell\|_{\text{HS}}^2 \le 0
as a quantum algorithm
(addendo: where it's coming from)
\text{Unitary } \hat U_\ell \text{ such that }
\hat W_\ell = [\Delta(\hat H_\ell),\sigma(\hat H_\ell)]
Głazek-Wilson-Wegner flow
\partial_\ell \|\sigma(\hat H_\ell)\|_{\text{HS}}^2 = -2\|\hat W_\ell\|_{\text{HS}}^2 \le 0
as a quantum algorithm
\hat H_\ell = \hat U_\ell \hat H_0 \hat U_\ell^\dagger
\partial_\ell \hat H_\ell = [\hat W_\ell, \hat H_\ell]
(addendo: where it's coming from)
New quantum algorithm for diagonalization
\hat H \mapsto \hat \mathcal H_\ell = \hat \mathcal U_\ell^\dagger \hat H \hat\mathcal U_\ell
\partial_\ell \hat \mathcal H_\ell = [[A(\hat \mathcal H_\ell),B(\hat \mathcal H_\ell)], \hat \mathcal H_\ell]
0
0
0
0
\hat D_s(\hat J) = \prod_{\mu\in\{0,1\}^{\times L}} \hat Z_\mu e^{-i s \hat J/D} \hat Z_\mu
\hat C_s(\hat J) = \left( \hat D_{\sqrt{s/K}}(\hat J)^\dagger \;e^{i\sqrt{s/K}\hat J}\;\hat D_{\sqrt{s/K}}(\hat J)\;e^{-i\sqrt{s/K}\hat J}\right)^K
1) Dephasing
2) Group commutator
3) Frame shifting
\partial_\ell \hat \mathcal H_\ell = [[A(\hat \mathcal H_\ell),B(\hat \mathcal H_\ell)], \hat \mathcal H_\ell]
\hat V_k = \hat C_s(\hat J_{1})\; \hat C_s(\hat J_{2})\ldots \hat C_s(\hat J_{k-1}) \approx e^{-s \hat W_1}\;e^{-s \hat W_2}\ldots e^{-s \hat W_{k-1}}
How to understand the continuous flow?
\hat H_1 = e^{s \hat W_1} \hat H e^{-s \hat W_1}
\hat W_1 = [\hat H,\sigma(\hat H)]
\hat W_k = [\hat H_{k-1},\sigma(\hat H_{k-1})]
\hat H_k = e^{s \hat W_k} \hat H_{k-1} e^{-s \hat W_k}
\hat H_\text{TFIM} = \sum_{i=1}^{L-1}\hat X_i\hat X_{i+1}+\sum_{i=1}^L \hat Z_i
Piece-wise constant GWW flow discretization
antihermitian
unitary
\left(i\hat H\right)^\dagger = -i \hat H
\hat W_k = [\hat D_{k-1},\hat H_{k-1}]
\hat H_k = e^{s_k \hat W_k} \hat H_{k-1} e^{-s_k \hat W_k}
Double-bracket iteration
s_k
Rotation durations:
Input:
\hat H_0
\hat D_k
Diagonal generators:
A new approach to diagonalization on a quantum computer
Great: we can diagonalize
How to quantum compile?
How to quantum?
Group commutator
\hat H \mapsto \hat \mathcal H_\ell = \hat \mathcal U_\ell^\dagger \hat H \hat\mathcal U_\ell
0
0
0
0
Want
\hat H_{k+1} = e^{s \hat W_k} \hat H_k e^{-s \hat W_k}
\hat W_k = [\hat D_k, \hat H_k]
e^{i\sqrt{s_k}\hat D_k}e^{i\sqrt{s_k}\hat H_k}e^{-i\sqrt{s_k}\hat D_k}e^{-i\sqrt{s_k}\hat H_k}= e^{-s[\hat D_k,\hat H_k]} +\hat E^\text{(GC)}
New bound
\|\hat E^\text{(GC)}\| \le 4\|\hat H_0\|\,\|[\hat D_k, \hat H_k]\| s^3
Group commutator
0
0
0
0
Frame shifting:
\hat H_{k} = \hat U_k^\dagger \hat H_0 \hat U_k
V_0 = e^{i\sqrt{s_0}\hat D_0}e^{i\sqrt{s_0}\hat H_0}e^{-i\sqrt{s_0}\hat D_0}e^{-i\sqrt{s_0}\hat H_0}
e^{-it \hat H_{k} } = e^{-t \hat U_k^\dagger \hat H_0 \hat U_k}= \hat U_k^\dagger e^{-t \hat H_0} \hat U_k
V_1 = e^{i\sqrt{s_1}\hat D_1}\hat V_{0}^\dagger e^{i\sqrt{s_1}\hat H_{0}}\hat V_0 e^{-i\sqrt{s_1}\hat D_1}V_{0}^\dagger e^{-i\sqrt{s_1}\hat H_{0}}\hat V_0
U_k = V_0 V_1 \ldots V_k
V_k = e^{i\sqrt{s_k}\hat D_k}\hat U_{k-1}^\dagger e^{i\sqrt{s_k}\hat H_{0}}\hat U_{k-1} e^{-i\sqrt{s_k}\hat D_k}\hat U_{k-1}^\dagger
e^{-i\sqrt{s_k}\hat H_{0}}\hat U_{k-1}
We get a recursive quantum algorithm:
the Hamiltonian tells us how to diagonalize itself
\hat W_k = [\hat D_{k-1},\hat H_{k-1}]
\hat H_k = e^{s_k \hat W_k} \hat H_{k-1} e^{-s_k \hat W_k}
Double-bracket iteration
s_k
Rotation durations:
Input:
\hat H_0
\hat D_k
Diagonal generators:
A new approach to diagonalization on a quantum computer
Great: we can diagonalize
How to quantum compile?
Replace by the group commutator
e^{-s[\hat D_k,\hat H_k]}\approx e^{i\sqrt{s}\hat D_k}e^{i\sqrt{s}\hat H_k}e^{-i\sqrt{s}\hat D_k}e^{-i\sqrt{s}\hat H_k}
Group commutator iteration
\hat V_k = e^{i\sqrt{s_k}\hat D_k}e^{i\sqrt{s_k}\hat H_k}e^{-i\sqrt{s_k}\hat D_k}e^{-i\sqrt{s_k}\hat H_k}
\hat H_{k+1} = \hat V_{k}^\dagger\hat H_{k} \hat V_k
\hat V_{k} = e^{-s[\hat D_{k},\hat H_{k}]}
Double-bracket iteration
Double-bracket iteration
Transition from theory to QPUs
How well does it work?
Variational flow example
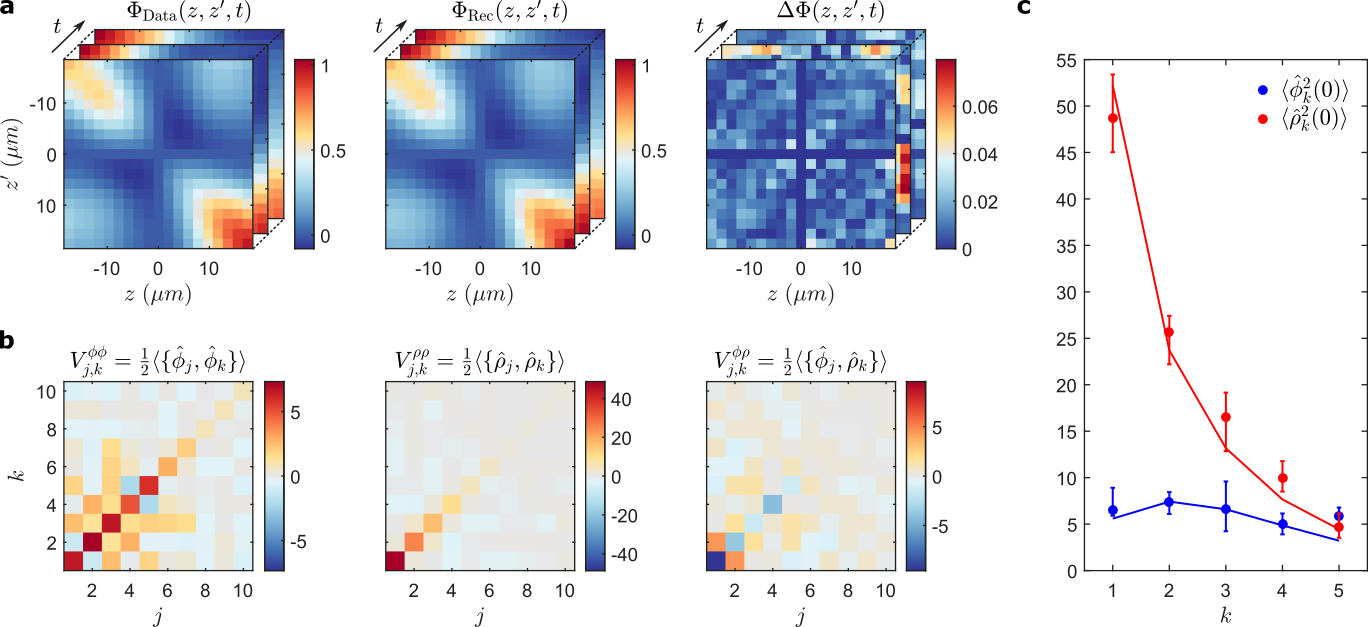
Notice the steady increase of diagonal dominance.
Variational vs. GWW flow
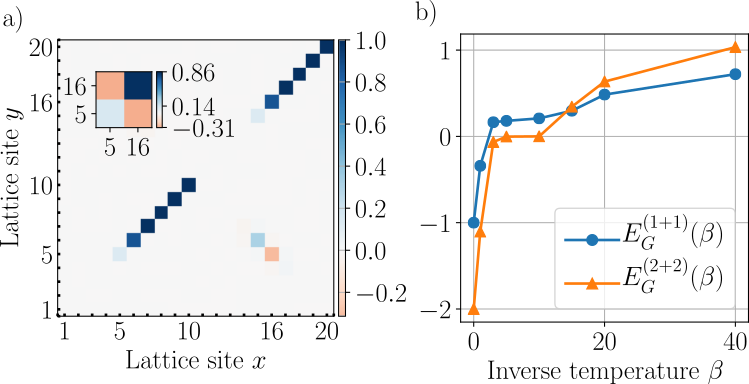
Notice that degeneracies limit GWW diagonalization but variational brackets can lift them.
GWW for 9 qubits
Notice the spectrum is almost converged.
How does it work again?
GWW for 9 qubits
Notice that some of them are essentially eigenstates!
How to dynamically program quantum?
Classical recursion
f_{k+1} = f_k+f_{k-1}
|\psi_{k+1}\rangle = U^{(\psi_k)} |\psi_k\rangle
For example:
U^{(\psi)} = 1 -2|\psi\rangle\langle \psi|
or
U^{(\psi )} = e^{is D} e^{is \hat \psi} e^{-is D}
Quantum recursion
Group commutator iterations
diagonalizing \(\hat \psi\)
are in this form
Quantum Dynamic Programming
- Memory usage query: trace out (consume) an instruction state
- Memory usage query: Repeat this procedure M times
\mathcal{E}_s^{(N,\rho)}(\sigma) = Tr_\rho [e^{-iNs} (\rho\otimes\sigma) e^{iNs}]
E^{(\mathcal{N},\rho)}(\sigma) = e^{i\mathcal{N}(\rho)} \sigma e^{-i\mathcal{N}(\rho)}
\mathcal{E}^{(\mathcal{N},\rho,M)}_{QDP} \coloneqq (\mathcal{E}^{(\mathcal{N},\rho)}_{1/M})^M = E^{(\mathcal{N},\rho)} + O(1/M)
Quantum recursion
|\psi_{k+1}\rangle = U^{(\psi_k)} |\psi_k\rangle
U^{(\psi_k)} = e^{i\mathcal{N}(\rho)}
- What we want memory call unitary:
- QDP does this by using memory usage query:
here \(N\) is the partial transpose of the Choi matrix of \(\mathcal N\)
Quantum Dynamic Programming
with J. Son, R. Takagi and N. Ng
QDP code structure
Talk on Tuesday
What's going on?
Double-bracket flow
Unitary
Satisfies a generalization of the Heisenberg equation
\hat H_\ell = \hat U_\ell^\dagger \hat H \hat U_\ell
\partial_\ell \hat H_\ell = [[A(\hat H_\ell),B(\hat H_\ell)], \hat H_\ell]
\hat U_\ell
GWW is a particular example
\partial_\ell \hat H_\ell = [[\Delta(\hat H_\ell),\sigma(\hat H_\ell)], \hat H_\ell]
transformation of
\hat H
\hat H_s = e^{s \hat W^{(Z)}} \hat H e^{-s \hat W^{(Z)}}
\hat W^{(Z)} = [\Delta^{(Z)}(\hat H), \hat H ],
\partial_s \|\sigma(\hat H_s)\|_{\text{HS}}^2 = -2\langle \hat W^{(Z)},\hat W\rangle_{\text{HS}}
\Delta^{(Z)}(\hat H) \text{ - diagonal}
Variational double-bracket flows
that are diagonalizing
\partial_\ell \|\sigma(\hat H_\ell)\|_{\text{HS}}^2 = -2\|\hat W_\ell\|_{\text{HS}}^2 \le 0
\hat J_0 = U_\theta^\dagger \hat H_0 U_\theta
Variational quantum circuits
boosted by
Variational double-bracket algorithms
with M. Robbiati, A. Pasquale,
E. Pedicillo, X. Li, A. Wright,
J. Son, K. U. Giang, S. T. Goh, J. Knörzer, J. Y. Khoo, N. Ng,
S. Carrazza
What else is there?
Linear programming
Matching optimization
Diagonalization
Sorting
QR decomposition
Toda flow
\partial_\ell \hat H_\ell = [[A(\hat H_\ell), B(\hat H_\ell)] , \hat H_\ell]
Double-bracket flow
Runtime-boosting heuristics
Analytical convergence analysis
Group commutator bound
Hasting's conjecture
Relation to other quantum algorithms
Code is available on Github
0
0
0
0
C
Double-bracket quantum algorithms for diagonalization
with J. Son, R. Takagi and N. Ng
\mathcal{E}^{(\mathcal{N},\rho,M)}_{QDP} \coloneqq (\mathcal{E}^{(\mathcal{N},\rho)}_{1/M})^M
Quantum dynamic programming
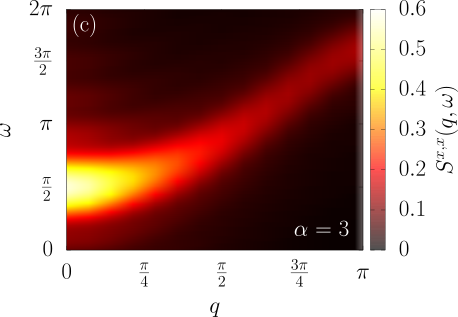
Material science?
0
0
0
0
C
How to dynamically quantum?
Group commutator
\hat H \mapsto \hat \mathcal H_\ell = \hat \mathcal U_\ell^\dagger \hat H \hat\mathcal U_\ell
\partial_\ell \hat \mathcal H_\ell = [[A(\hat \mathcal H_\ell),B(\hat \mathcal H_\ell)], \hat \mathcal H_\ell]
0
0
0
0
Want
\hat H_1 = e^{s \hat W_1} \hat H e^{-s \hat W_1}
\hat W_1 = [\Delta(\hat H),\sigma(\hat H)]
e^{is\Delta(\hat H)}e^{is\hat H}e^{-is\Delta(\hat H)}e^{-is\hat H}= e^{-s^2[\Delta(\hat H),\sigma(\hat H)]} +\hat E^\text{(GC)}
New bound
\|\hat E^\text{(GC)}\| \le 4\|\hat H\|\,\|[\Delta(\hat H),\sigma(\hat H)]\| s^3
Group commutator
\hat H \mapsto \hat \mathcal H_\ell = \hat \mathcal U_\ell^\dagger \hat H \hat\mathcal U_\ell
\partial_\ell \hat \mathcal H_\ell = [[A(\hat \mathcal H_\ell),B(\hat \mathcal H_\ell)], \hat \mathcal H_\ell]
0
0
0
0
Want
\hat H_1 = e^{s \hat W_1} \hat H e^{-s \hat W_1}
\hat W_1 = [\Delta(\hat H),\sigma(\hat H)]
e^{is\Delta(\hat H)}e^{is\hat H}e^{-is\Delta(\hat H)}e^{-is\hat H}= e^{- s^2[\Delta(\hat H),\sigma(\hat H)]} +\hat E^\text{(GC)}
How to get ?
\hat D_s(\hat H) \approx e^{is\Delta(\hat H)}
\hat C_s(\hat J) = \hat D_{\sqrt{s}}(\hat J)^\dagger \; e^{i\sqrt{s}\hat J}\; \hat D_{\sqrt{s}}(\hat J)\; e^{-i\sqrt{s}\hat J}
\approx e^{-s \hat W(\hat J)}
1,
1,
1,
1,
0,
0,
0,
0
Phase flip unitaries
\mu = (
)
N
S
N
S
N
S
N
S
\hat Z
\mathbb 1
\mathbb 1
\otimes
\otimes
\otimes
\otimes
\otimes
\otimes
\otimes
\hat Z
\hat Z
\hat Z
\mathbb 1
\mathbb 1
0,
1,
0,
1,
0,
0,
0,
1
\mu = (
)
1
\otimes
\mathbb 1
\otimes
\mathbb 1
\otimes
\hat Z
\otimes
1
\otimes
\mathbb 1
\otimes
\hat Z
\otimes
\hat Z
N
S
N
S
N
S
Phase flip unitaries
Evolution under dephased generators
\hat H \mapsto \hat H_\ell = \hat U_\ell^\dagger \hat H \hat U_\ell
\partial_\ell \hat H_\ell = [[A(\hat H_\ell),B(\hat H_\ell)], \hat H_\ell]
0
0
0
0
\hat Z_\mu e^{-i s \hat J} \hat Z_\mu = e^{-is \hat Z_\mu \hat J\hat Z_\mu}
\hat D_s(\hat J) \approx \prod_{\mu\in R} \hat Z_\mu e^{-i s \hat J/D} \hat Z_\mu
We can make it efficient:
\Delta(\hat J)= \frac 1 {\dim (\hat J)} \sum_{\mu\in\{0,1\}^{\times L}} \hat Z_\mu \hat J \hat Z_\mu
R \subseteq \{0,1\}^{\times L}
Use unitarity
and repeat many times
New quantum algorithm for diagonalization
\hat H \mapsto \hat \mathcal H_\ell = \hat \mathcal U_\ell^\dagger \hat H \hat\mathcal U_\ell
\partial_\ell \hat \mathcal H_\ell = [[A(\hat \mathcal H_\ell),B(\hat \mathcal H_\ell)], \hat \mathcal H_\ell]
0
0
0
0
\hat D_s(\hat J) = \prod_{\mu\in\{0,1\}^{\times L}} \hat Z_\mu e^{-i s \hat J/D} \hat Z_\mu
\hat C_s(\hat J) = \left( \hat D_{\sqrt{2s/K}}(\hat J)^\dagger \;e^{i\sqrt{2s/K}\hat J}\;\hat D_{\sqrt{2s/K}}(\hat J)\;e^{-i\sqrt{2s/K}\hat J}\right)^K
\hat V_k = \hat V_{k-1}\hat C_s(\hat J_{k-1})
\hat J_{k-1} = \hat V_{k-1}^\dagger \hat H \hat V_{k-1}
1) Dephasing
2) Group commutator
3) Frame shifting
\partial_\ell \hat \mathcal H_\ell = [[A(\hat \mathcal H_\ell),B(\hat \mathcal H_\ell)], \hat \mathcal H_\ell]
\hat V_k = \hat C_s(\hat J_{1})\; \hat C_s(\hat J_{2})\ldots \hat C_s(\hat J_{k-1}) \approx e^{-s \hat W_1}\;e^{-s \hat W_2}\ldots e^{-s \hat W_{k-1}}