Lecture:
Quantum compiling
Marek Gluza
NTU Singapore
slides.com/marekgluza

*Explanation of the background explanation: It's a wall built from primitive bricks - there is a similarity to how a quantum circuit is built from gates and how in an experiment these gates can be quite clumsy!

Scan QR code or use the URL to load these slides - there will be lot's of links!
What is our quantum computer?
What is a universal quantum computer?
1 qubit
2 qubits
3 qubits
4 qubits
And you get the idea lah
we will approximate via circuits
It's all about the group of unitary matrices
What is a quantum algorithm?
0
0
0
0
C
What is a quantum computer?
It's an experimental setup A which includes a quantum system B and that setup A allows to manipulate the quantum state of B.

What is a quantum algorithm?
0
0
0
0
C
What is a universal quantum computer?
It's an experimental setup which includes a quantum system and that setup allows to manipulate its quantum state.
It's an experimental setup which includes few-level quantum systems and that setup allows to manipulate the quantum state using gates.
These gates form a universal gate set which means that if you apply sufficiently many you will be able to reach any desired quantum state.
What are quantum gates?
What are quantum gates?

Useful notation
Exercise: By evaluating the determinant, prove that it's impossible to apply Z in the lab
What are quantum gates?
Use the quantum computer to transform
into
Trivial quantum algorithm solves it:
Apply the Haddamard gate
0
What are all single qubit quantum gates?
What are 2 qubit quantum gates?
Use the quantum computer to transform
into
Apply the Haddamard gate on each qubit
0
0
What are quantum gates?
Use the quantum computer to transform
into
Apply the Haddamard gate on each qubit
and then apply the controlled-not gate
0
0

Universal gate set "Ising + single qubit"
0
0
0
0
Universal gate set #2
Universal gate set #3: Surface code
About CZ
About CZ
Exercise: derive this using the Hilbert-Schmidt scalar product.
Implementing CZ
0
0
0
0
Exercise: Use commutation relations and BCH formula to implement CZ with the Ising gate set
All 2 qubit operations
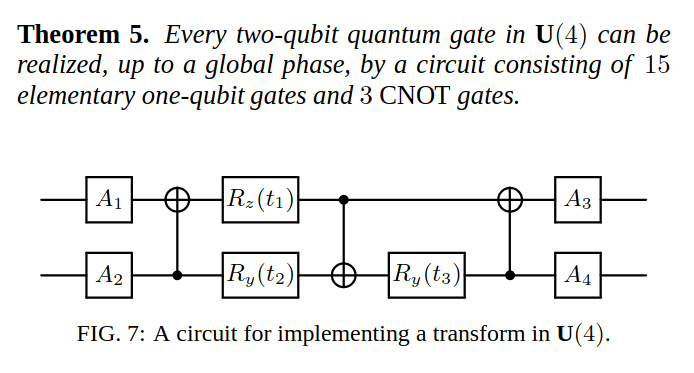
About CNOT
+
Swap gate from CNOT

Universality is generic:
Universal gate set "Ising + single qubit"
0
0
0
0
How can we use it to implement any unitary?
Universal quantum computation
How can we use it to implement any unitary?
Implement its Hamiltonian

Implementing Hamiltonians
Hermitian matrices are a vector space
Is a basis
Orthonormal
expansion

In the exam* you will prove
Is a basis
How to get

* This is super important, so what if it was on some exam? Could you prove it?

In the exam you will prove
Is a basis
How to get
Universal quantum computation

Universal quantum computation
Trotter-Suzuki decomposition
0
0
0
0
Trotter-Suzuki decomposition
Why does it work?
BCH formula
Conclusion: For short evolution time we're happy
How to implement Trotter-Suzuki?
Use Solovay-Kitaev algorithm to compile these gates but usually they are the primitive gates
0
0
0
0
Exercise: Local error bound
Exercise: Non-commutative identity
cf.:
Application to physics:
Universal quantum computation
Constructive quantum compilation
How to get
Clifford circuits
For every
There exists
Such that
Super crucial exam formula
Super crucial exclam formula
Super cool exciting formula

Super cool exclam formula
In this (insane) model: all we ever do is make infinitesimally small rotations on qubit 1 and then distribute that onto all the other qubits using Clifford operations
Surely, there must be better ways?!

Addendum: Clifford circuits
For every
There exists
Such that

Addendum: formal definition Clifford circuits
This is called the Pauli group
Addendum: formal definition Clifford circuits
Pauli operators have essentially the same spectrum
There must be unitary operators mapping them to each other
Addendum: formal definition Clifford circuits
All you need is single qubit and CNOTs

How to compute it on a laptop?
How to compute it on a quantum computer?
Hamiltonian simulation
How to compute it on a laptop?
For qubits, your laptop can do ~13 spins at finite temperature and ~25 spins for a pure state (use sparsity)
At the end of the day:
Workarounds:
Hamiltonian simulation
How to compute it on a quantum computer?
Use quantum algorithms 'Hamiltonian simulation'
Trotter-Suzuki
Linear combination of unitaries
Qubitization
Randomized compiler
Hamiltonian simulation
Truncated series

P: Runs easily
BPP: Often runs easily
BQP: Often quantums easily
NP: Optimizes easily


QMA

P: Runs easily
BPP: Often runs easily
BQP: Often quantums easily
NP: Optimizes easily
Key idea for post-Trotter methods
Step 1: Show that it's unitary
Key idea for post-Trotter methods
Step 2: Apply to flag qubit in superposition
Key idea for post-Trotter methods
Step 3: Consider what happens if applied to superposition:
Key idea for post-Trotter methods
Step 4: Assume flag is measured with outcome 1 and discard it
Conclusion: We can (probabilistically) apply (normalized) sums of unitary operators
Key idea for reliable post-Trotter methods
Grover reflector
Step 1: Show that it's unitary
Key idea for reliable post-Trotter methods
Grover reflector
Step 2: Consider applying it to a state overlapping with it
Key idea for reliable post-Trotter methods
Grover reflector
Step 3: Reflect around the linear combination of unitaries
This is also called oblivious amplitude amplification, and the crux is in making this efficiently and obliviously i.e. without knowing or destroying the reflector state
Gaussian quantum simulators
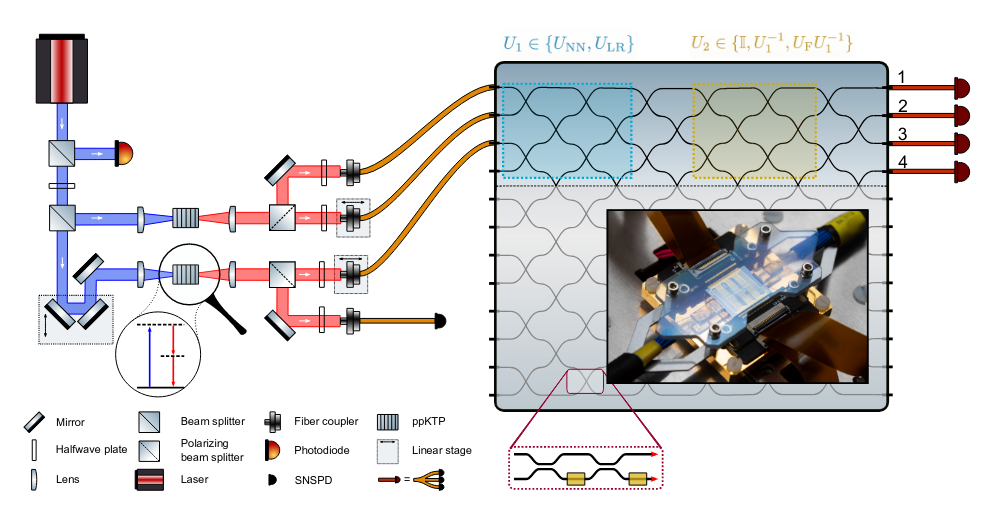










How?




Ultra-cold 1d gases





Inside: atoms
Outside: wavepackets
hydrodynamics



Energy of phonons




Tomonaga-Luttinger liquid


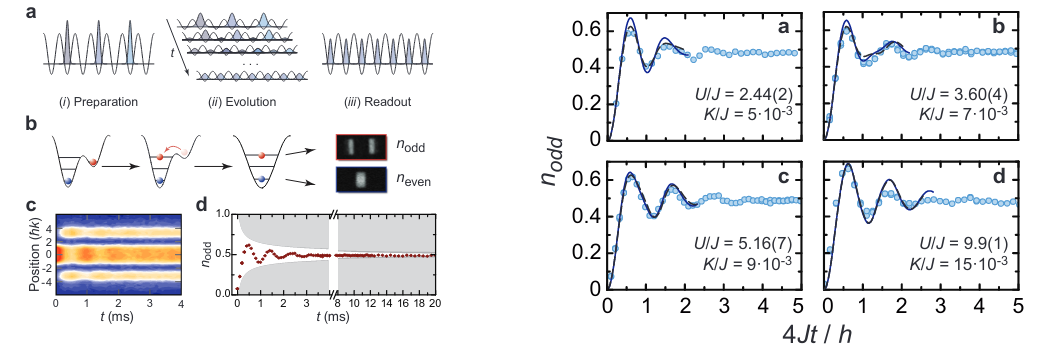
Quantum field refrigerators in the TLL model:
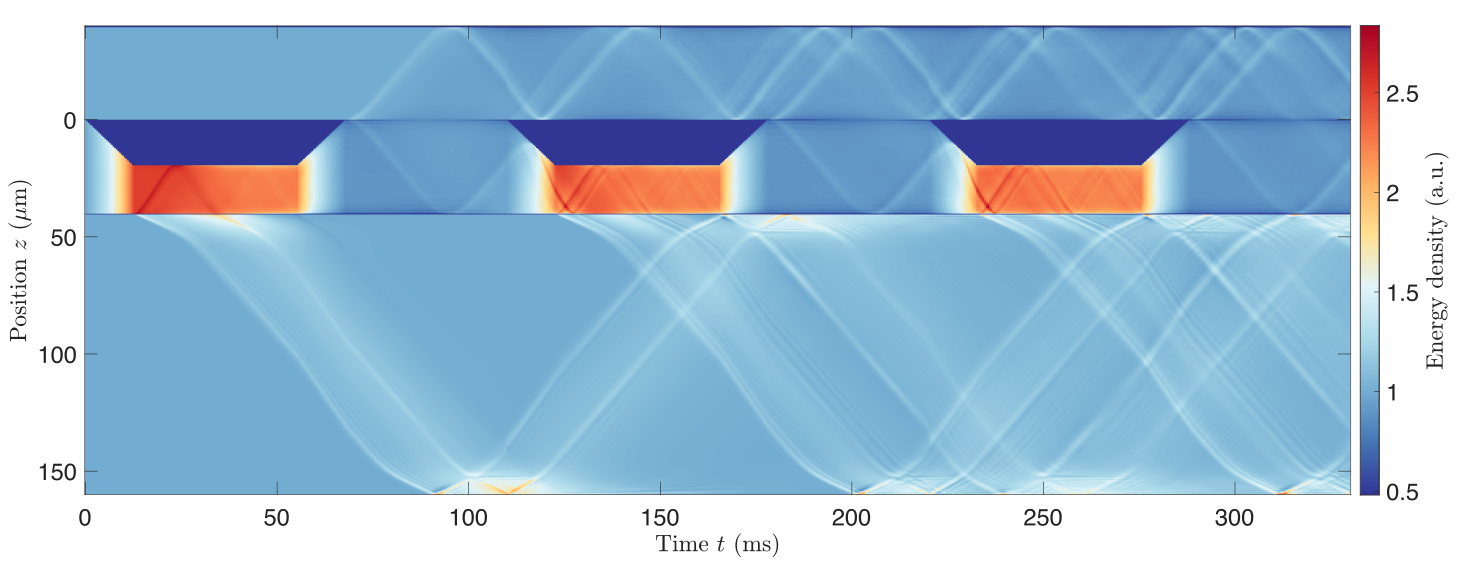
System
Piston
Bath
Bath with excitations
System cooled down
Breaking of the Huygens-Fresnel principle
in the inhomogenous TLL model:
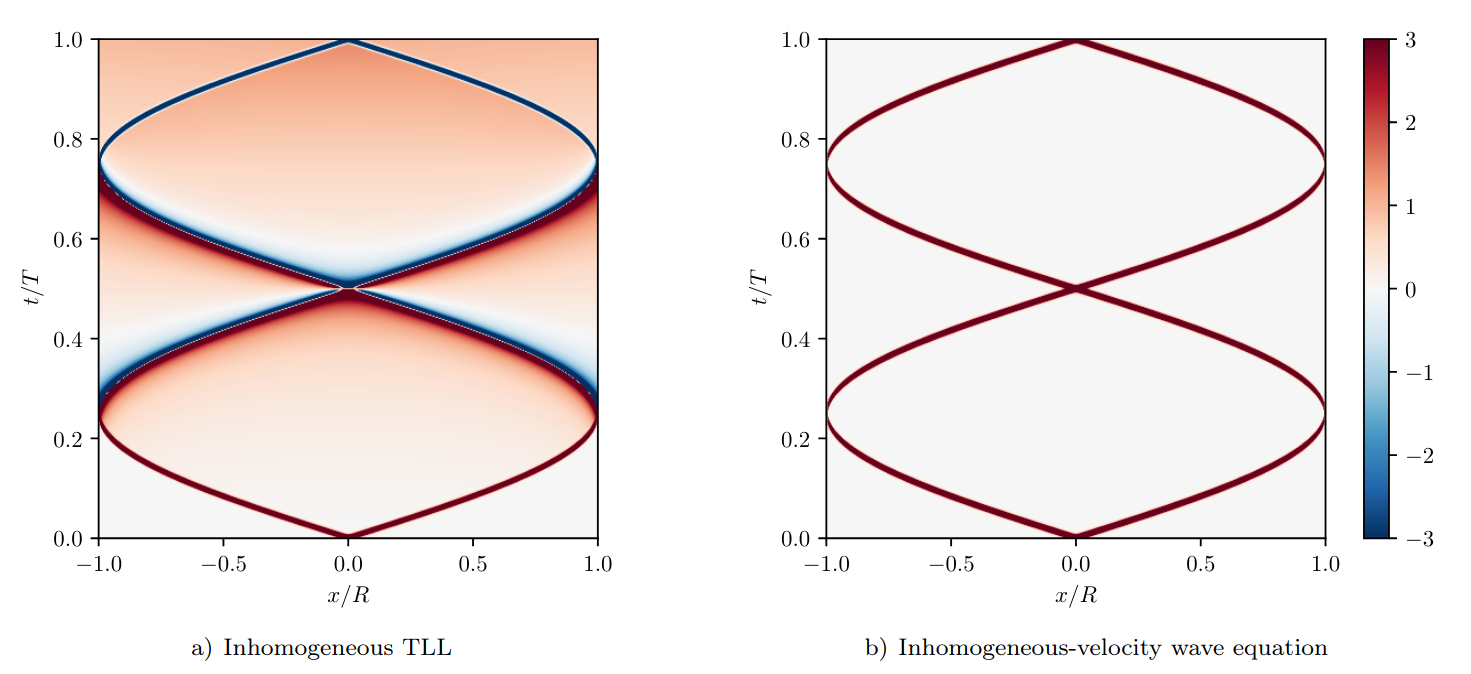

Why?
Why develop continuous field
quantum simulators?
- Representation theory: Quantum information?
- Continuum limits: BQP and QMA or more?
- Are nanowires computationally hard to simulate?
What do we know is difficult?



SM
Fundamental
Universal
Effective


Why develop continuous field
quantum simulators?
- Representation theory: Quantum information?
- Continuum limits: BQP and QMA or more?
- Are nanowires computationally hard to simulate?
What do we know is difficult?



SM
Fundamental
Universal
Effective

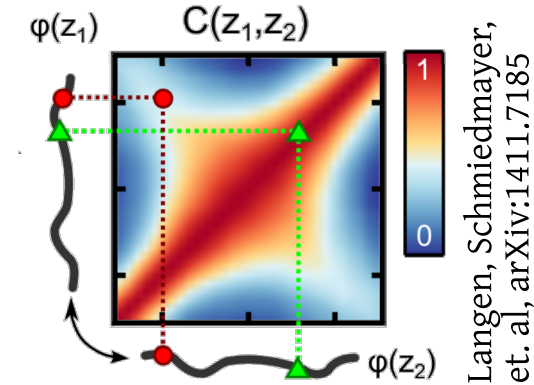
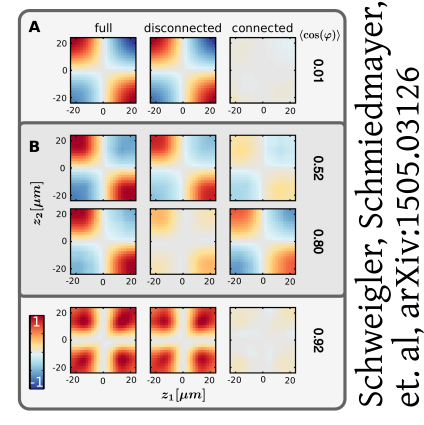
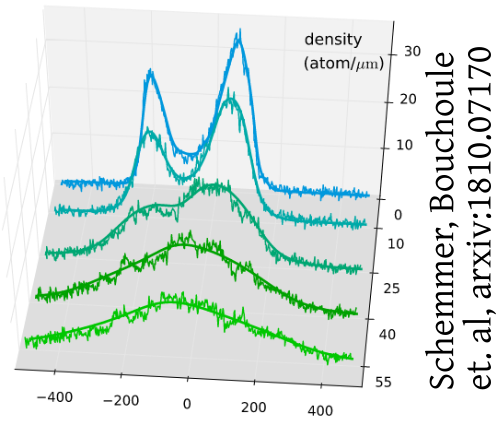
Non-thermal
steady states
Sine-Gordon
thermal states
Atomtronics
Generalized hydrodynamics
Recurrences
Some highlights:
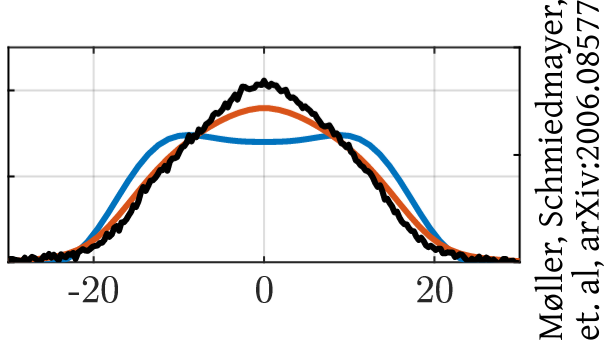
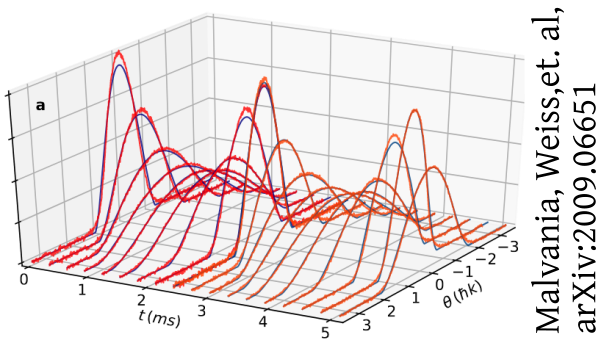
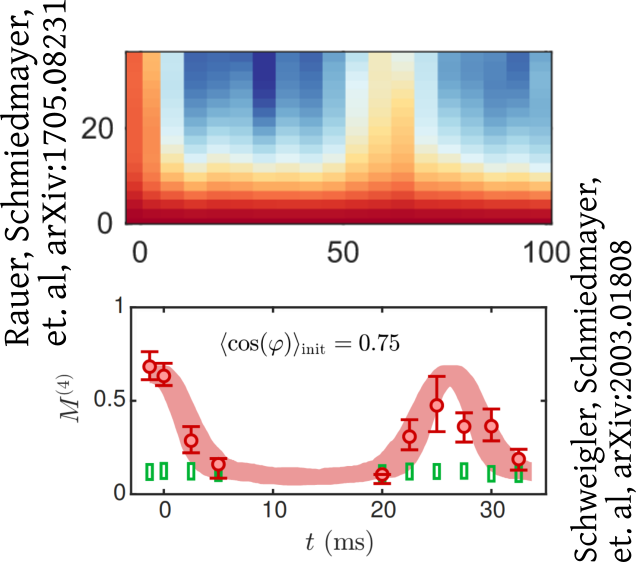
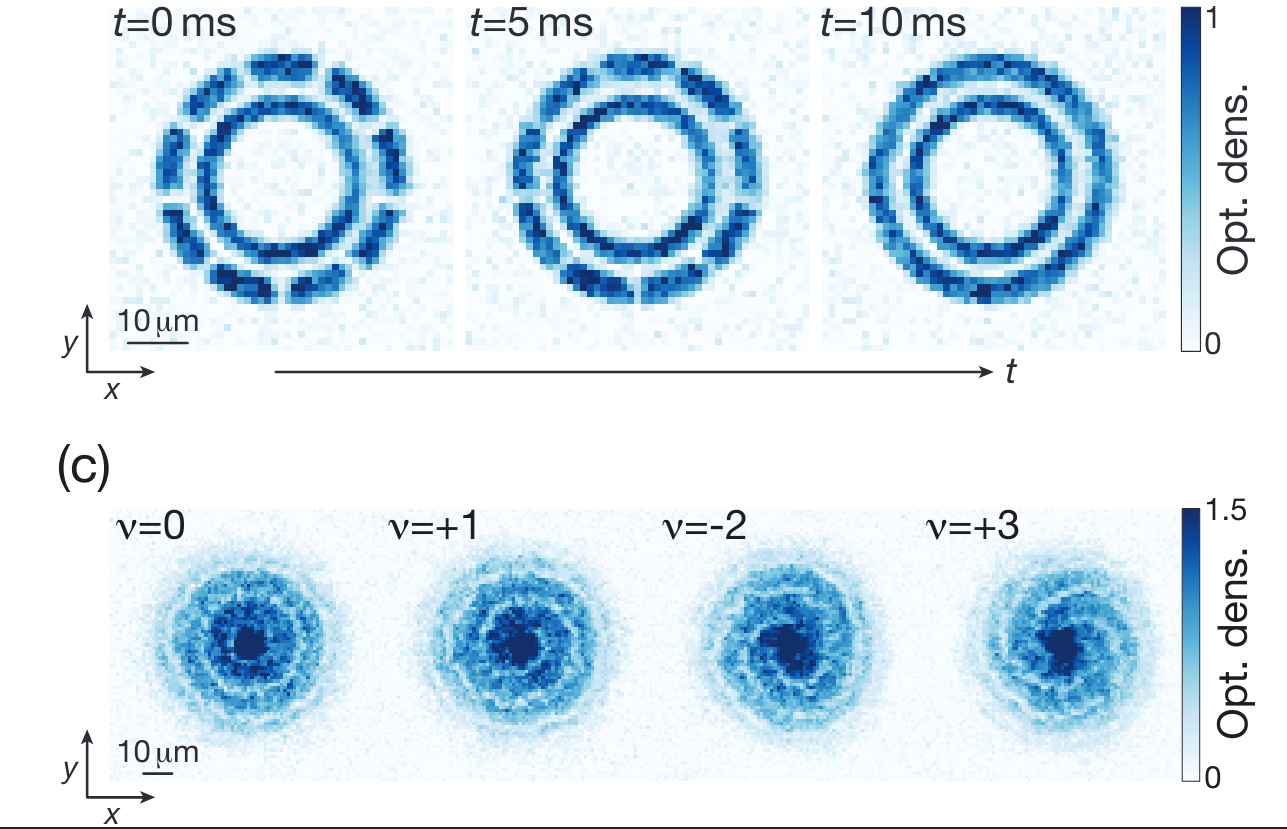

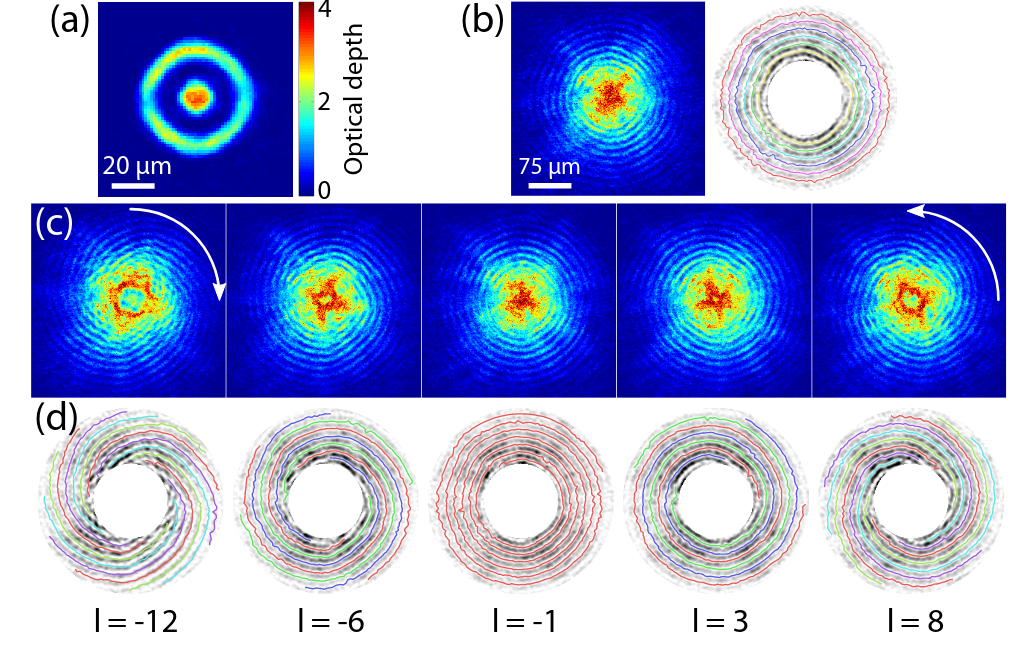
Interferometry measures velocities

van Nieuwkerk, Schmiedmayer, Essler, arXiv:1806.02626
Schumm, Schmiedmayer, Kruger, et al., arXiv:quant-ph/0507047
Tomography
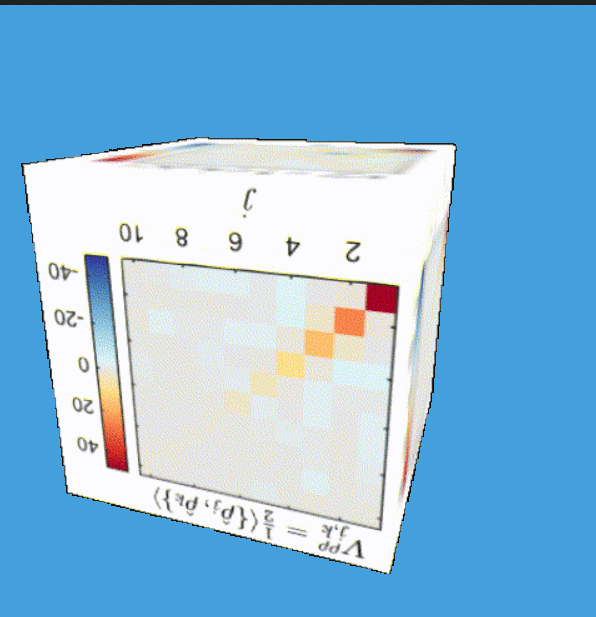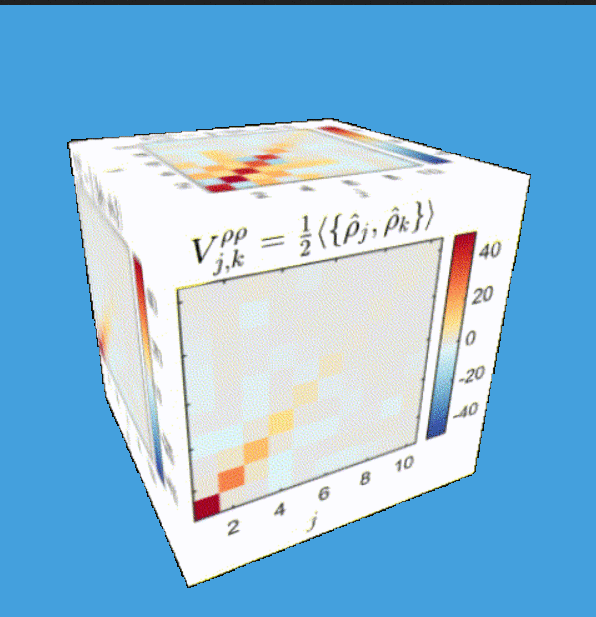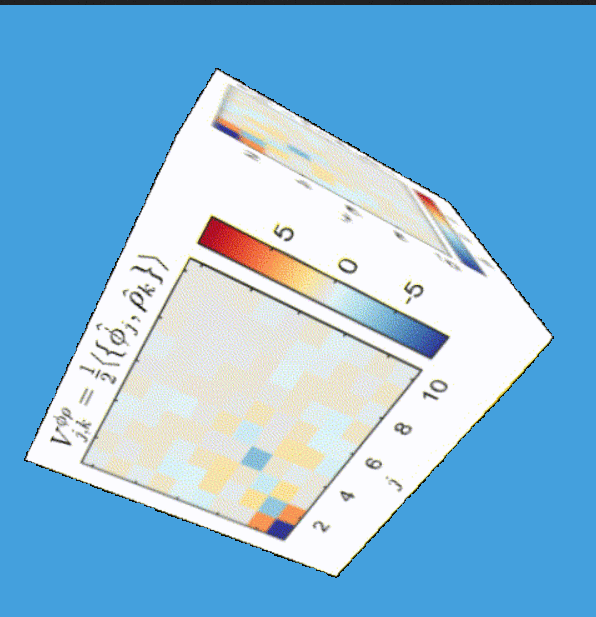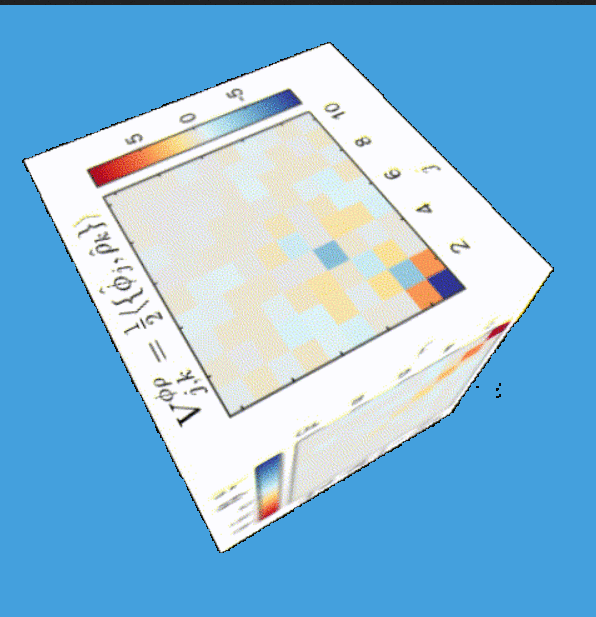
Tomography for phonons

Tomography for phonons

What are eigenmodes?
Transmutation

Tomography
(This formalism: Tomography for many modes)

Tomography Klein-Gordon thermal state after quench
Extracting physical properties
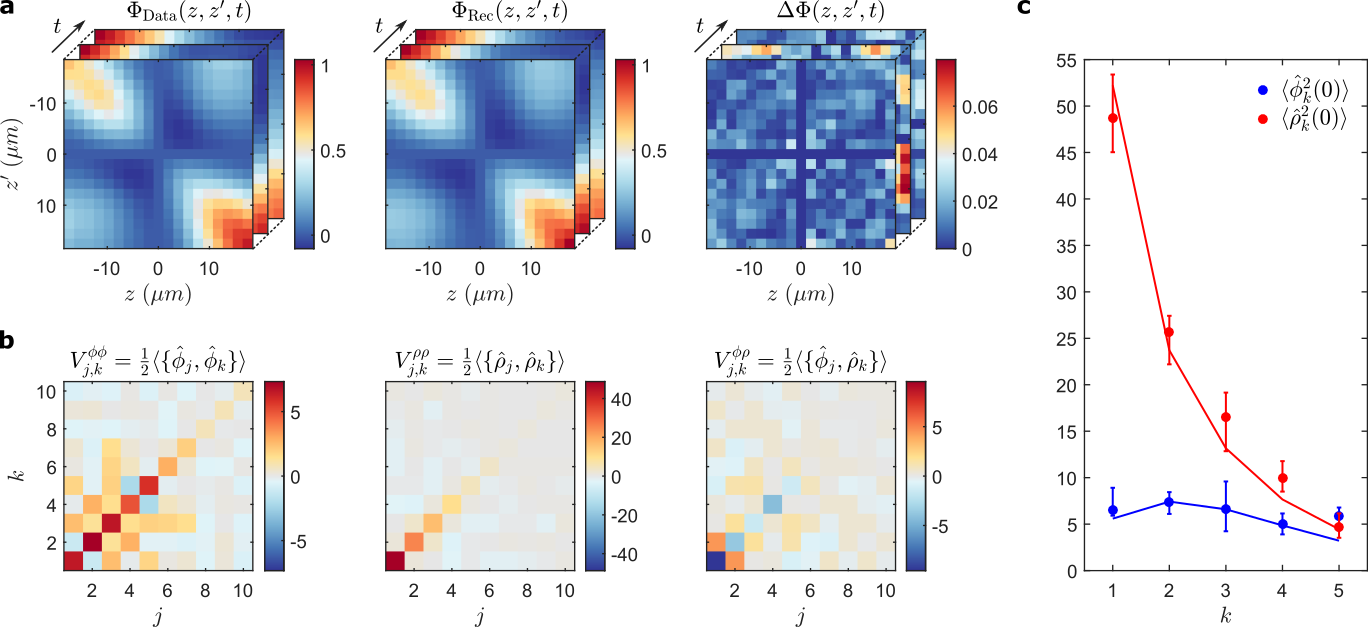
Extracting physical properties
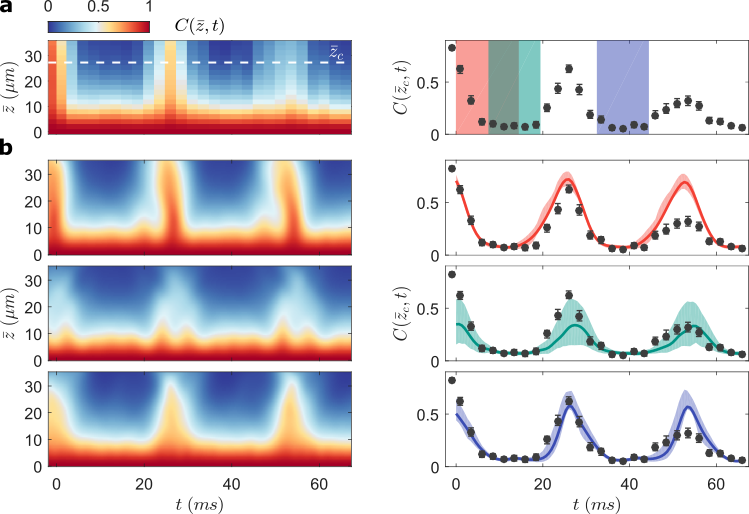
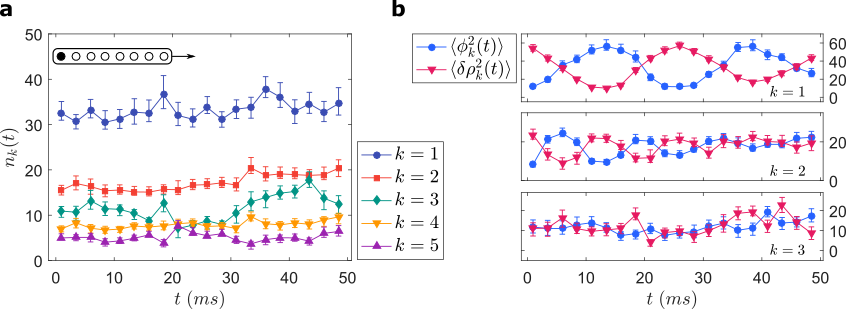
Extracting physical properties
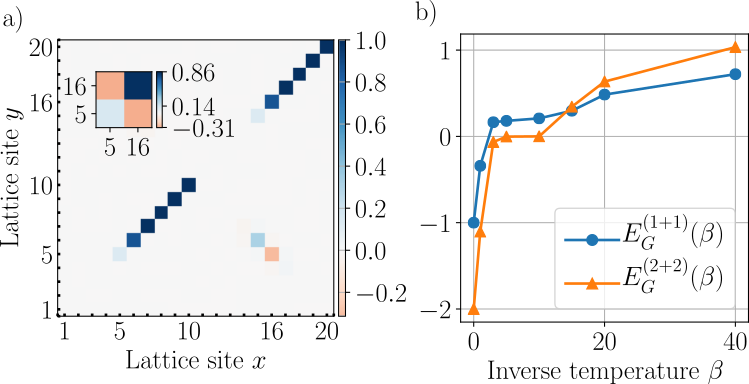
Tomography for optical lattices








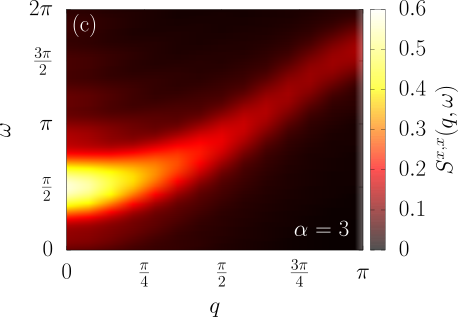
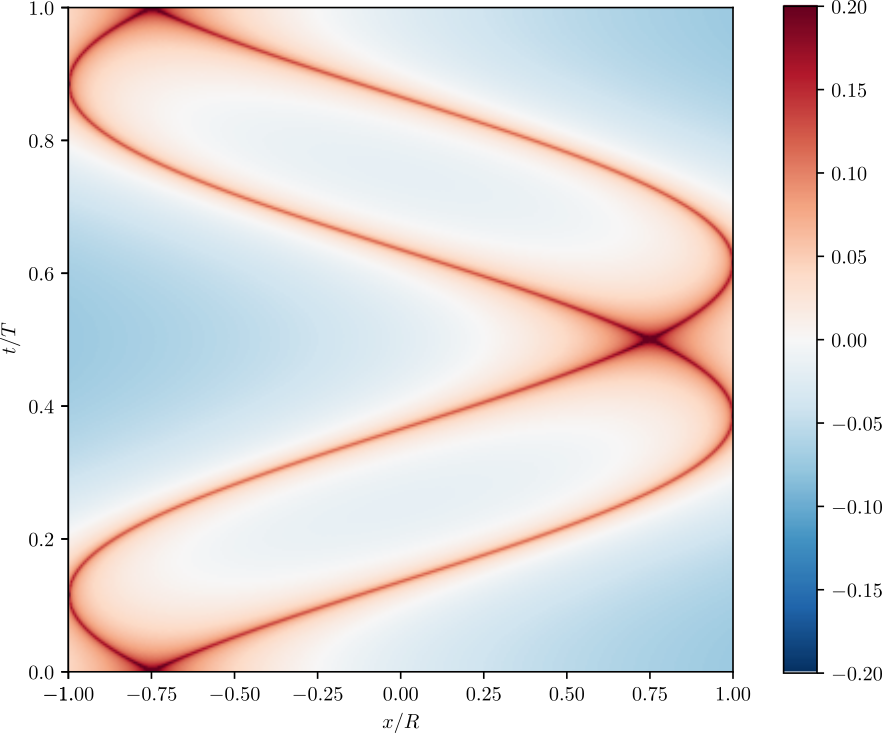
Material science?
0
0
0
0
C


Diagonalization quantum algorithm
DSF of Rydberg arrays
Phonon tomography
Optical lattice tomography







Ask me anytime:
0
0
0
0
C

Fidelity witnesses
Tomography optical lattices
Tomography phonons
Proving statistical mechanics
Quantum simulating DSF
Holography in tensor networks
PEPS contraction average #P-hard
Quantum field machine
MBL l-bits
(click links at slides.com/marekgluza