Quantum algorithms tutorial using QIBO

Marek Gluza

NTU Singapore

slides.com/marekgluza

Quantum algorithms tutorial using QIBO

Marek Gluza

NTU Singapore

slides.com/marekgluza

What is a quantum algorithm?

\hat H \mapsto \hat \mathcal H_\ell = \hat \mathcal U_\ell^\dagger \hat H \hat\mathcal U_\ell
\partial_\ell \hat \mathcal H_\ell = [[A(\hat \mathcal H_\ell),B(\hat \mathcal H_\ell)], \hat \mathcal H_\ell]

0

0

0

0

C

What is a quantum computer?

It's an experimental setup A which includes a quantum system B and that setup A allows to manipulate the quantum state of B.

What is a quantum algorithm?

\hat H \mapsto \hat \mathcal H_\ell = \hat \mathcal U_\ell^\dagger \hat H \hat\mathcal U_\ell
\partial_\ell \hat \mathcal H_\ell = [[A(\hat \mathcal H_\ell),B(\hat \mathcal H_\ell)], \hat \mathcal H_\ell]

0

0

0

0

C

What is a universal quantum computer?

It's an experimental setup which includes a quantum system and that setup allows to manipulate its quantum state.

It's an experimental setup which includes few-level quantum systems and that setup allows to manipulate the quantum state using gates.

These gates form a universal gate set which means that if you apply sufficiently many you will be able to reach any desired quantum state.

What is our quantum computer?

\hat H \mapsto \hat \mathcal H_\ell = \hat \mathcal U_\ell^\dagger \hat H \hat\mathcal U_\ell
\partial_\ell \hat \mathcal H_\ell = [[A(\hat \mathcal H_\ell),B(\hat \mathcal H_\ell)], \hat \mathcal H_\ell]

What is a universal quantum computer?

|\psi\rangle = a | 0 \rangle + b | 1\rangle
|\psi\rangle = a | 00 \rangle + b | 10\rangle+c | 01 \rangle + b | 11\rangle
|\psi\rangle = a | 000 \rangle + b | 100\rangle+c | 010 \rangle + d | 100\rangle+ e | 011 \rangle + f | 101\rangle+g | 110 \rangle +h | 111\rangle
|\psi\rangle = a | 0000 \rangle + b | 1000\rangle+c | 0100 \rangle + d | 1000\rangle+ e | 0011 \rangle + f | 0101\rangle+g | 1010 \rangle +h | 1100\rangle + \ldots

1 qubit

2 qubits

3 qubits

4 qubits

And you get the idea lah

In the circuit model we will apply gates. Today we will see some special examples.

What are quantum gates?

|\psi\rangle = a | 0 \rangle + b | 1\rangle
|+\rangle = \frac 1 {\sqrt 2} (| 0 \rangle + | 1\rangle)

How to quantum?

What are quantum gates?

|\psi\rangle = | 0 \rangle
Z|0\rangle = | 0\rangle

How does it work again?

What are quantum gates?

|\psi\rangle = | 0 \rangle
|+\rangle = \frac 1 {\sqrt 2} (| 0 \rangle + | 1\rangle)

Use the quantum computer to transform

into

Trivial quantum algorithm solves it:

Apply the Haddamard gate

H = \frac 1 {\sqrt 2} \begin{pmatrix} 1 & 1 \\ 1 &- 1\end{pmatrix}

0

H

1 qubit is boring, 10 qubits are challenging, 100 qubits are worth

the buzz

What are quantum gates?

|\psi\rangle = | 0 \rangle \otimes |0\rangle
|+\rangle \otimes |+\rangle = \frac 1 { 2} (| 0 0\rangle + | 01\rangle+|10\rangle + | 11\rangle)

Use the quantum computer to transform

into

Apply the Haddamard gate on each qubit

H\otimes H

0

H

0

H

What are quantum gates?

|\psi\rangle = | 0 \rangle \otimes |0\rangle
|\Phi\rangle = \frac 1 { \sqrt 2} (| 0 0\rangle + | 11\rangle)

Use the quantum computer to transform

into

Apply the Haddamard gate on each qubit

H\otimes 1

and then apply the controlled-not gate

\text{CNOT} = |0\rangle\langle 0|\otimes 1 + |1\rangle\langle1 |\otimes X
H

0

0

+

What else is there?

What are quantum algorithms?

|\psi\rangle
|\langle \phi |\psi\rangle|^2

Use the quantum computer to transform

into their fidelity

|\phi\rangle

and

as an encoded in a measured expectation value

How well does it work?

What is quantum compiling?

Controlled-SWAP

Use the quantum computer to transform

into the

and

CNOT
Controlled-CNOT

https://quantumcomputing.stackexchange.com/questions/9342/how-to-implement-a-fredkin-gate-using-toffoli-and-cnots

New quantum algorithm for diagonalization

\hat H \mapsto \hat \mathcal H_\ell = \hat \mathcal U_\ell^\dagger \hat H \hat\mathcal U_\ell
\partial_\ell \hat \mathcal H_\ell = [[A(\hat \mathcal H_\ell),B(\hat \mathcal H_\ell)], \hat \mathcal H_\ell]

building useful quantum algorithms

new approach to preparing useful states

building useful variational circuits

tons of fun maths in the appendix

no qubit overheads

no controlled-unitaries

0

0

0

0

arXiv:2206.11772

Bridging the gap between theoretical quantum algorithms and experimental actualities

Next 2 years theory support for prof. Rainer Dumke as NTU PPF (super-conducting qubits, tomography zoo, proof-of-principle quantum algorithms...)

Student internships available,

I'm coordinating an undergrad study group and a graduate-level research seminar

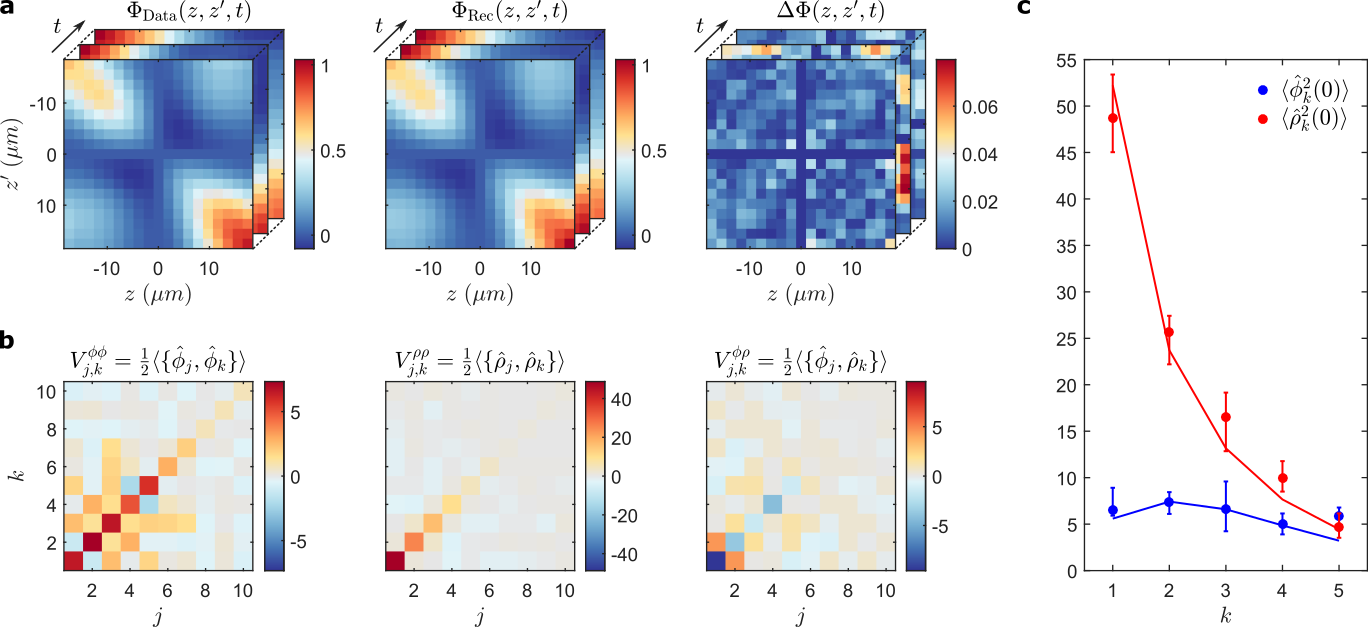
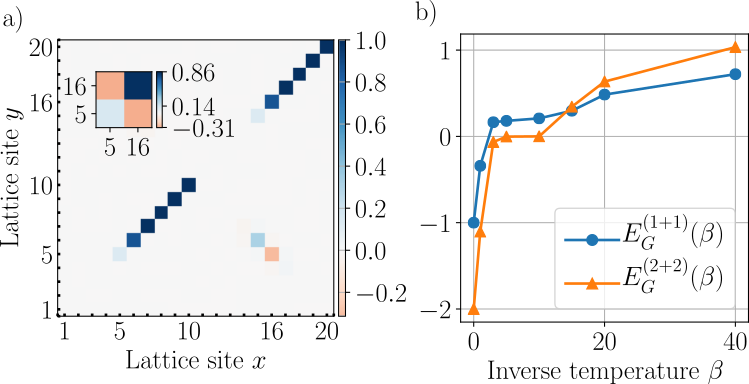
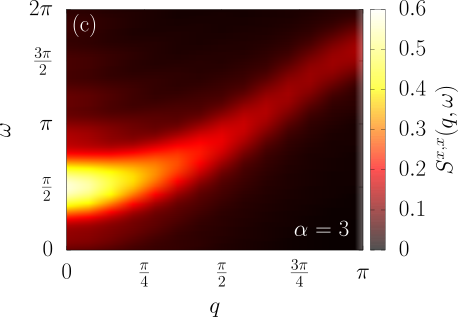
Material science?

0

0

0

0

C

arXiv:2206.11772

arxiv:1912.06076

arxiv:2005.09000

arxiv:1807.04567