Lecture:
Quantum
simulation
Marek Gluza
NTU Singapore
slides.com/marekgluza

How to compute it on a laptop?
How to compute it on a quantum computer?
Hamiltonian simulation
How to compute it on a laptop?
For qubits, your laptop can do ~13 spins at finite temperature and ~25 spins for a pure state (use sparsity)
At the end of the day:
Workarounds:
Hamiltonian simulation
How to compute it on a quantum computer?
Use quantum algorithms 'Hamiltonian simulation'
Trotter-Suzuki
Linear combination of unitaries
Qubitization
Randomized compiler
Hamiltonian simulation
Truncated series

P: Runs easily
BPP: Often runs easily
BQP: Often quantums easily
NP: Optimizes easily


QMA

P: Runs easily
BPP: Often runs easily
BQP: Often quantums easily
NP: Optimizes easily
Trotter-Suzuki decomposition
Trotter-Suzuki decomposition
Why does it work?
BCH formula
Conclusion: For short evolution time we're happy
How to implement Trotter-Suzuki?
Use Solovay-Kitaev algorithm to compile these gates but usually they are the primitive gates
0
0
0
0
Hamiltonian simulation
0
0
0
0
0
0
0
0
C
Most sophisticated theoretical methods use
controlled-unitary operations
Exercise: Local error bound
Exercise: Non-commutative identity
cf.:
Application to physics:
Key idea for post-Trotter methods
Step 1: Show that it's unitary
Key idea for post-Trotter methods
Step 2: Apply to flag qubit in superposition
Key idea for post-Trotter methods
Step 3: Consider what happens if applied to superposition:
Key idea for post-Trotter methods
Step 4: Assume flag is measured with outcome 1 and discard it
Conclusion: We can (probabilistically) apply (normalized) sums of unitary operators
Key idea for reliable post-Trotter methods
Grover reflector
Step 1: Show that it's unitary
Key idea for reliable post-Trotter methods
Grover reflector
Step 2: Consider applying it to a state overlapping with it
Key idea for reliable post-Trotter methods
Grover reflector
Step 3: Reflect around the linear combination of unitaries
This is also called oblivious amplitude amplification, and the crux is in making this efficiently and obliviously i.e. without knowing or destroying the reflector state
Gaussian quantum simulators
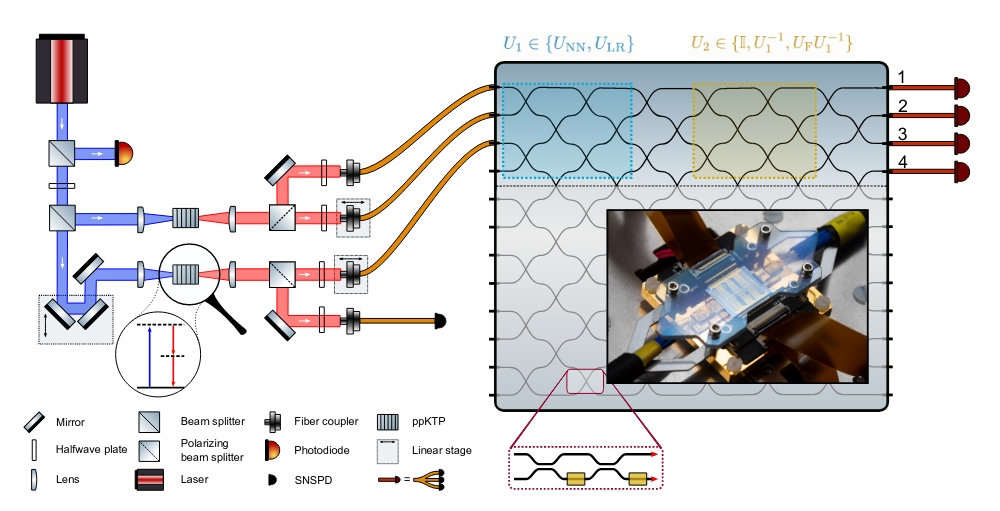










How?




Ultra-cold 1d gases





Inside: atoms
Outside: wavepackets
hydrodynamics



Energy of phonons




Tomonaga-Luttinger liquid


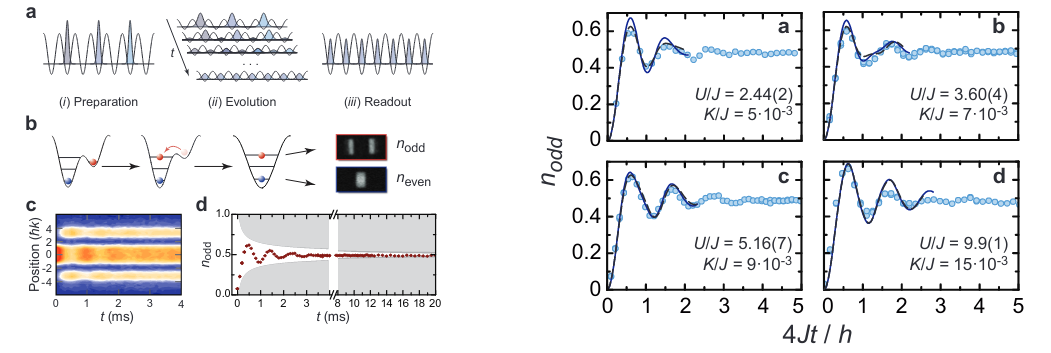
Quantum field refrigerators in the TLL model:
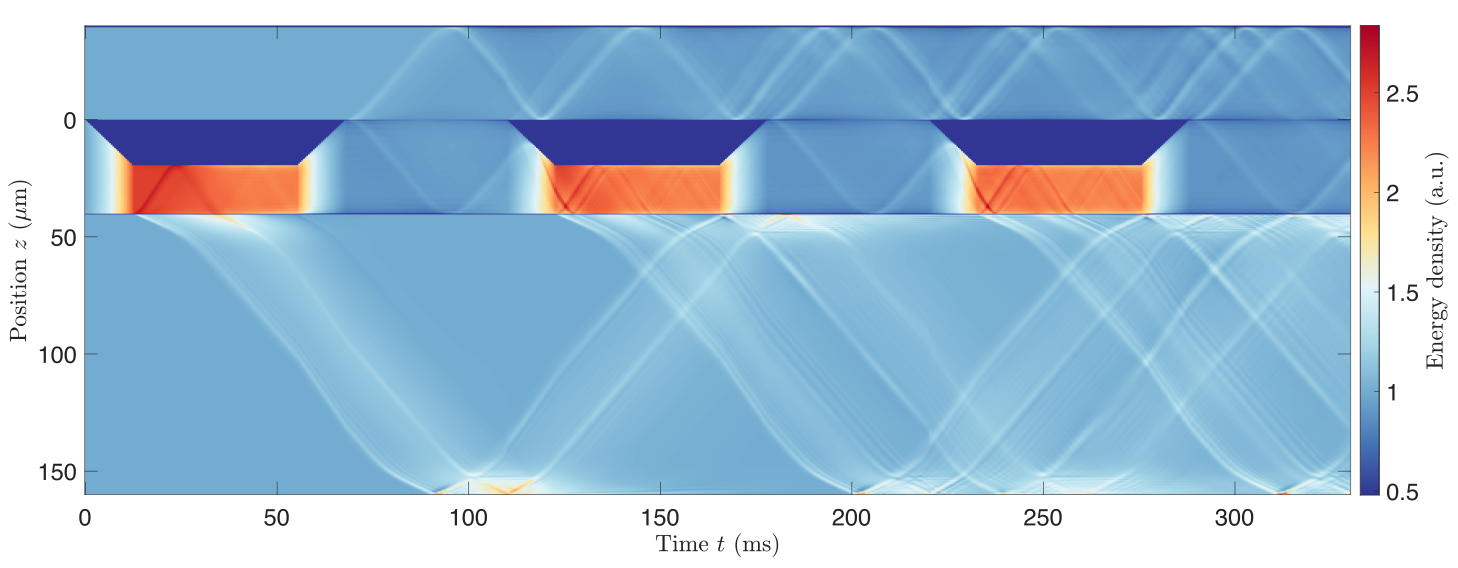
System
Piston
Bath
Bath with excitations
System cooled down
Breaking of the Huygens-Fresnel principle
in the inhomogenous TLL model:
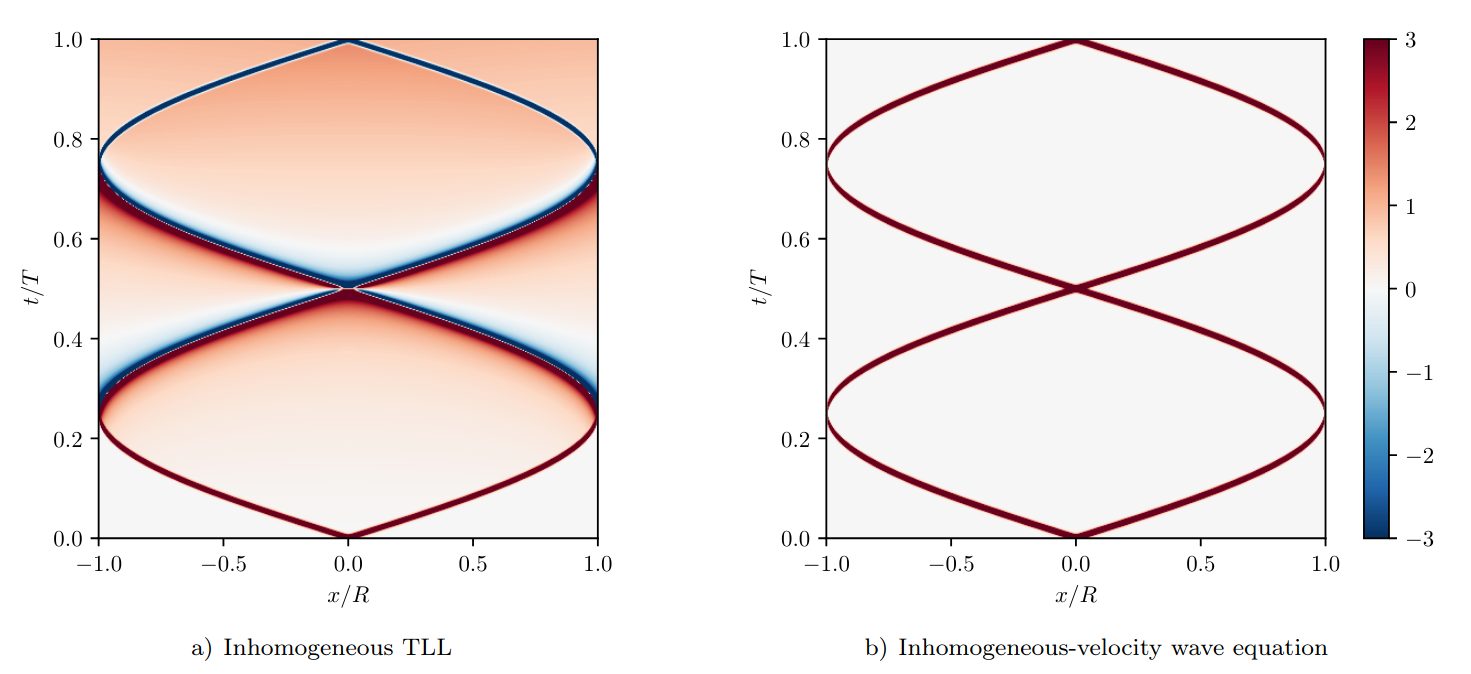

Why?
Why develop continuous field
quantum simulators?
- Representation theory: Quantum information?
- Continuum limits: BQP and QMA or more?
- Are nanowires computationally hard to simulate?
What do we know is difficult?



SM
Fundamental
Universal
Effective


Why develop continuous field
quantum simulators?
- Representation theory: Quantum information?
- Continuum limits: BQP and QMA or more?
- Are nanowires computationally hard to simulate?
What do we know is difficult?



SM
Fundamental
Universal
Effective

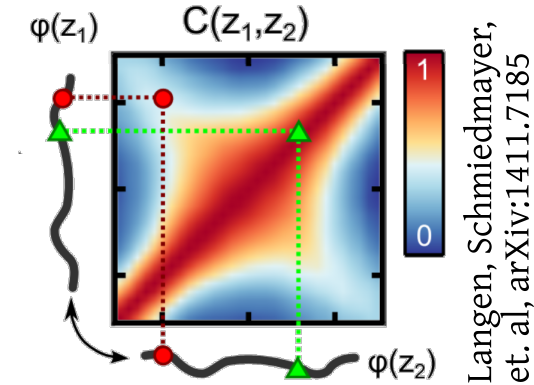
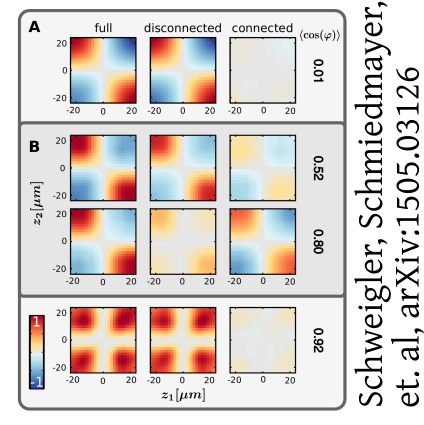
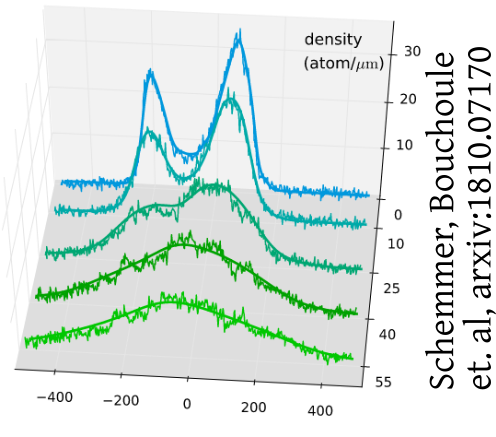
Non-thermal
steady states
Sine-Gordon
thermal states
Atomtronics
Generalized hydrodynamics
Recurrences
Some highlights:
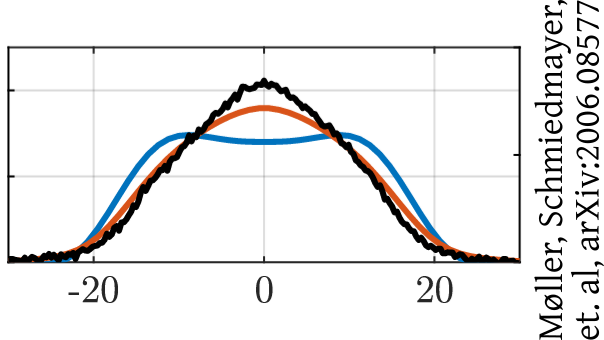
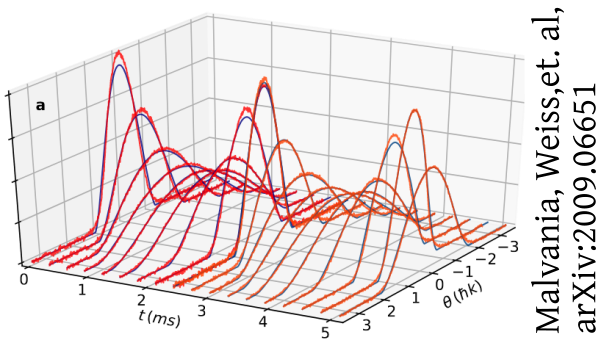
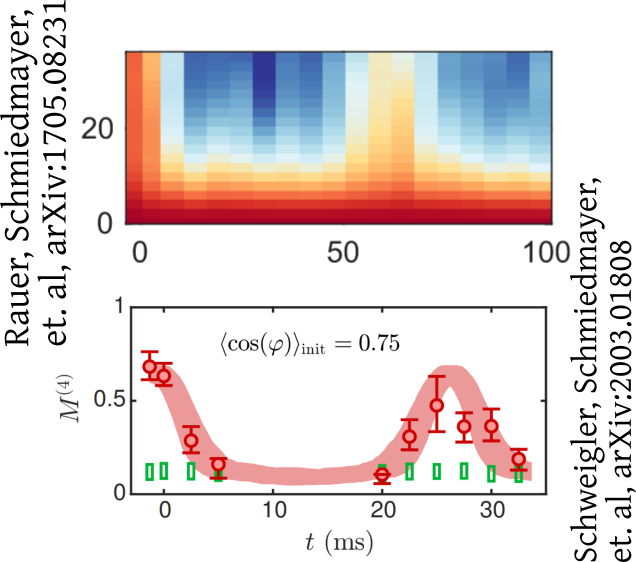
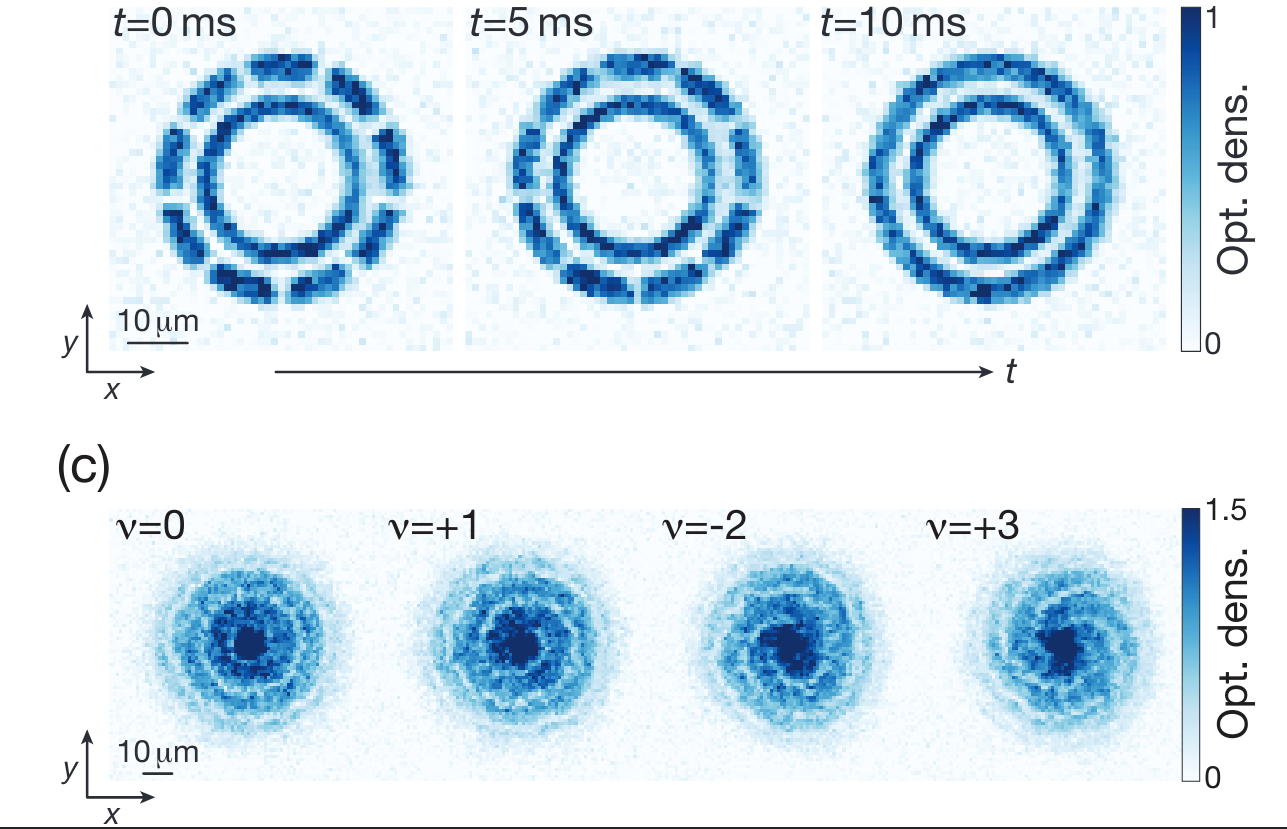

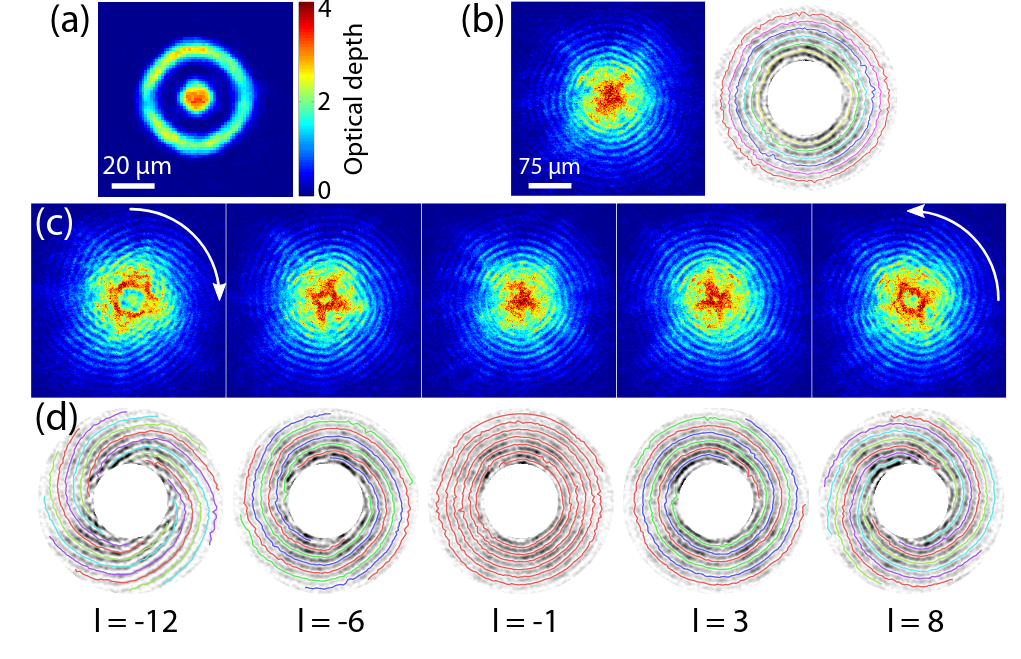
Interferometry measures velocities

van Nieuwkerk, Schmiedmayer, Essler, arXiv:1806.02626
Schumm, Schmiedmayer, Kruger, et al., arXiv:quant-ph/0507047
Tomography
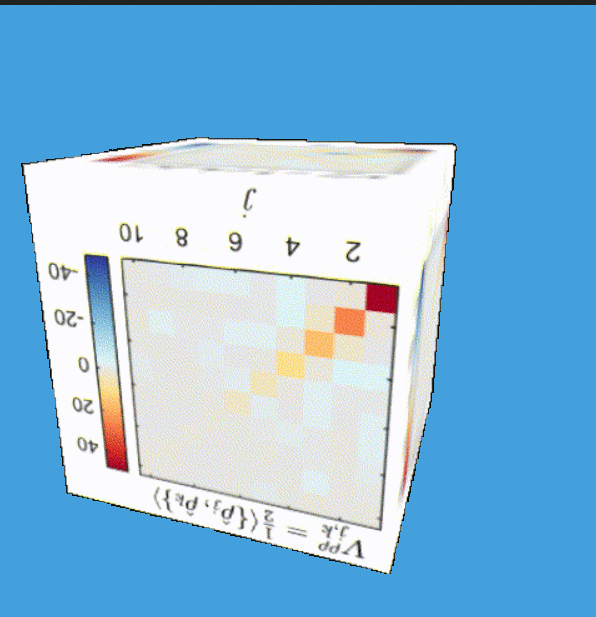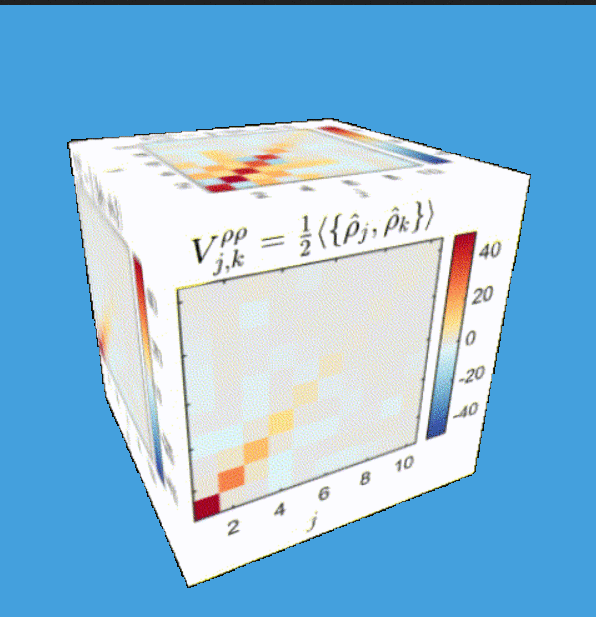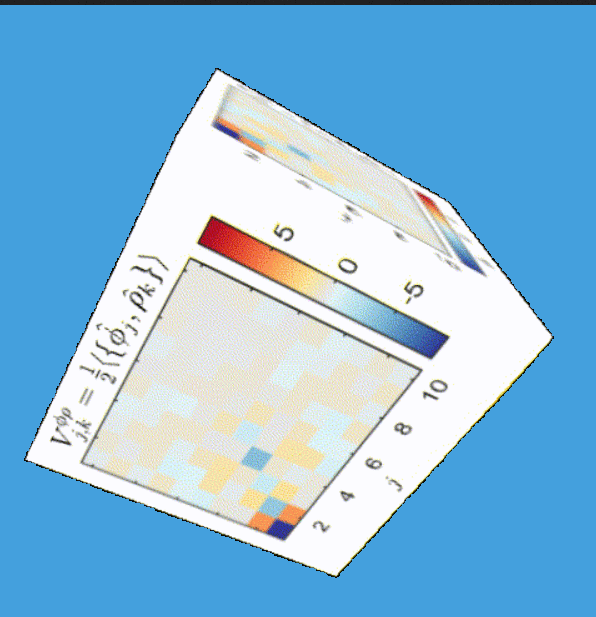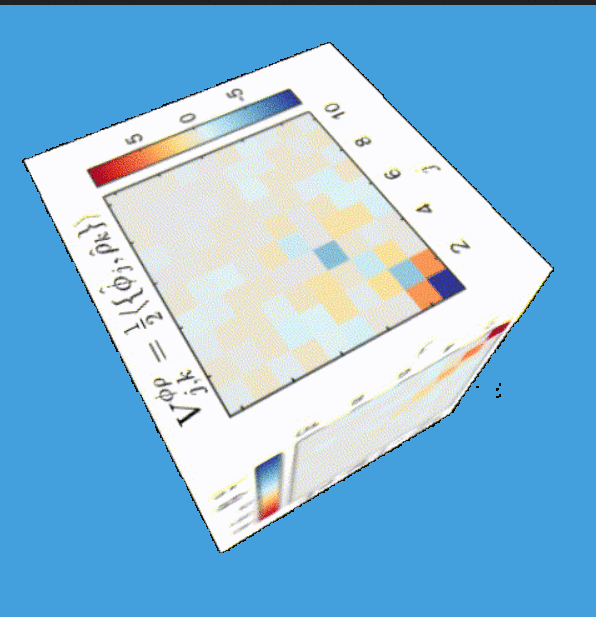
Tomography for phonons

Tomography for phonons

What are eigenmodes?
Transmutation

Tomography
(This formalism: Tomography for many modes)

Tomography Klein-Gordon thermal state after quench
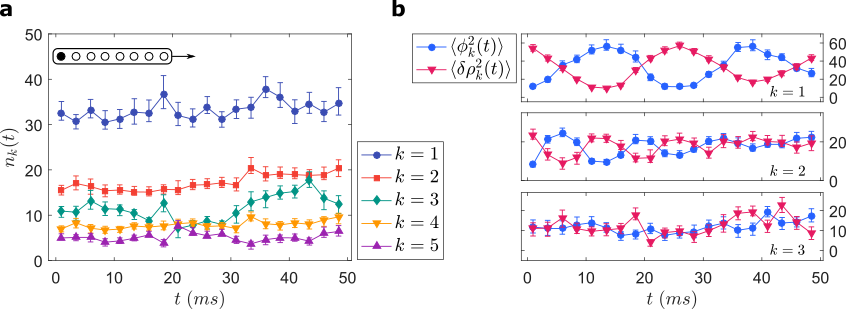
Extracting physical properties
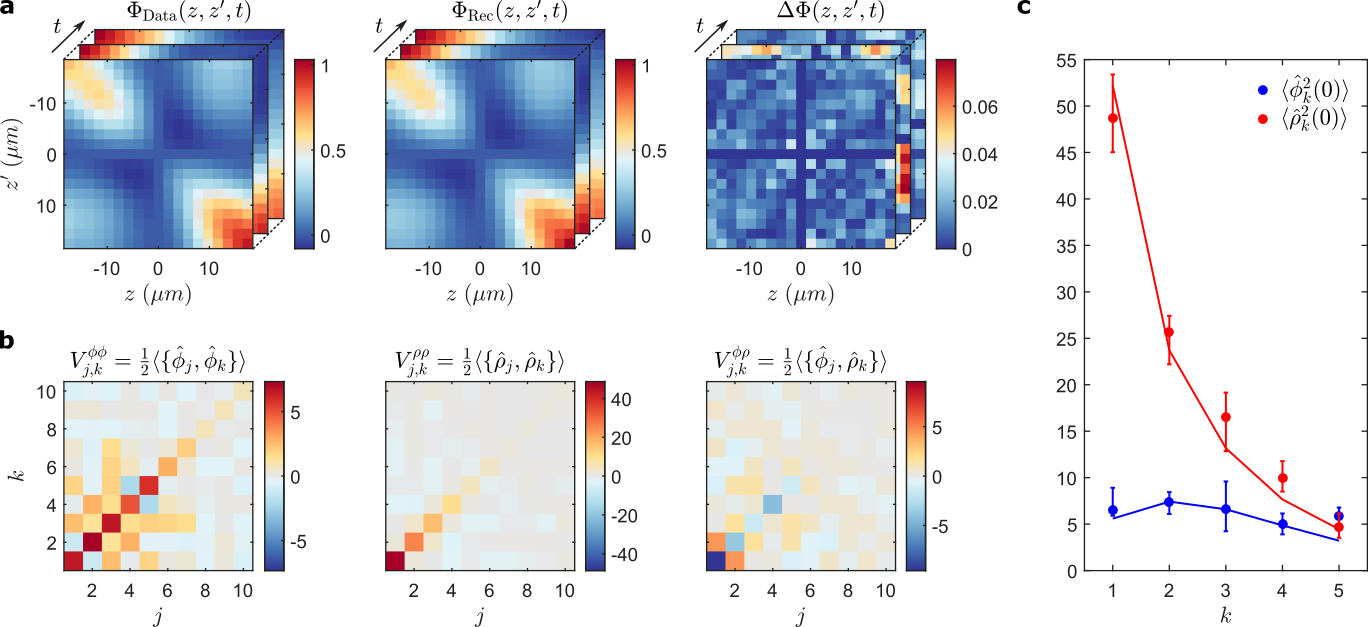
Extracting physical properties
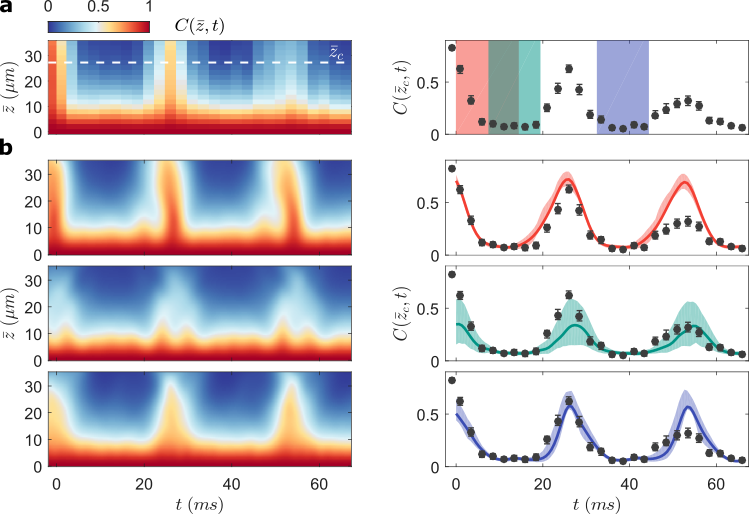
Extracting physical properties
Tomography for optical lattices

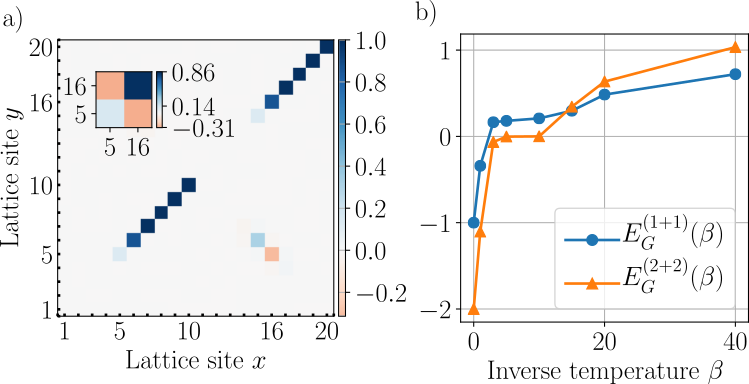







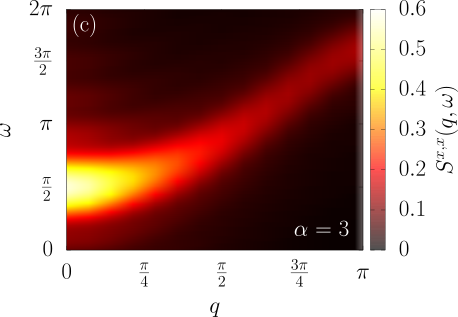
Material science?
0
0
0
0
C


Diagonalization quantum algorithm
DSF of Rydberg arrays
Phonon tomography
Optical lattice tomography







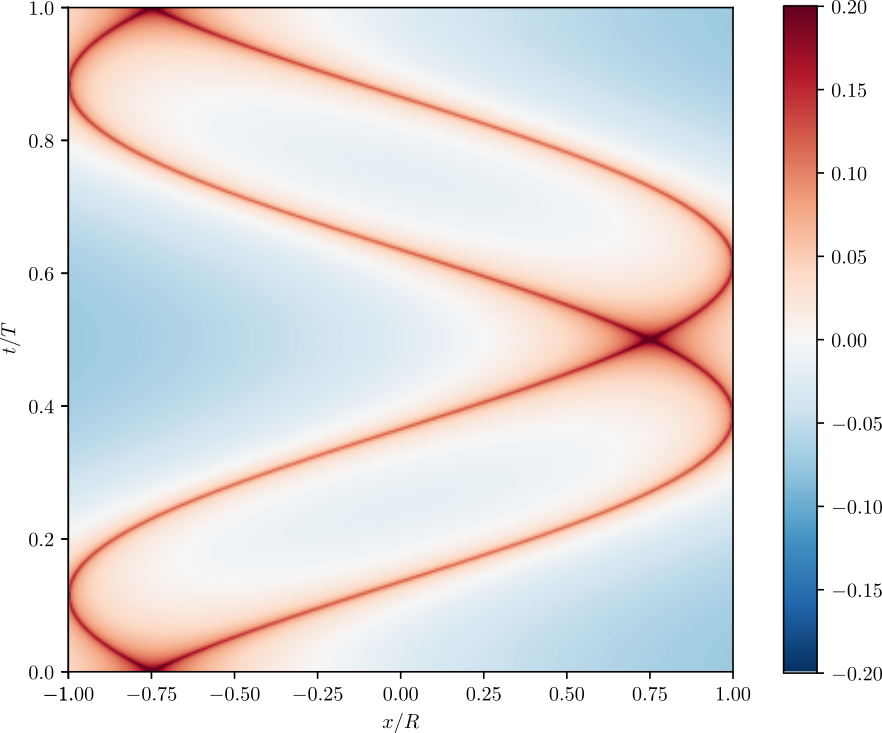
Ask me anytime:
0
0
0
0
C

Fidelity witnesses
Tomography optical lattices
Tomography phonons
Proving statistical mechanics
Quantum simulating DSF
Holography in tensor networks
PEPS contraction average #P-hard
Quantum field machine
MBL l-bits
(click links at slides.com/marekgluza