NTK evolution
First experiment
Architecture: wide resnet
Dataset: CIFAR10
archive 4% error (close to SOTA)
with 2 classes it archive 2.8% error
without
- batch normalization
- weight decay
- learning rate scheduler
- cross entropy (linear hinge instead)
it archive 6% error

-
binary classification (automobile, cat, dog, horse and truck vs the rest)
-
6k images
-
no batch normalization
-
no weight decay
-
no learning rate scheduler
-
linear hinge instead of cross entropy
it archive 20.7% error and 0 train loss
train with the frozen kernel (same dynamics)
\(\Theta\frac{P}{\|\Theta\|}\)

Kernel inflation

rem.: inflation of the kernel justifies learning rate decay
\(df = \partial_0 f dw + \partial_0^2 f dw^2 + \partial_0^3 f dw^3 + \mathcal{O}(dw^4)\)
\(1 \sim \alpha df \sim \alpha dw \Rightarrow dw \sim \alpha^{-1}\)
\(\Theta \sim (\partial f)^2 \sim (\partial_0 f + \partial_0^2 f dw + \partial_0^3 f dw^2 + \mathcal{O}(dw^3))^2 \sim \Theta_0 + \partial_0 f \partial_0^2 f dw + (\partial_0^2 f dw)^2 + \partial_0 f \partial_0^3 f dw^2 + \mathcal{O}(dw^3)\)
\(d\Theta \sim \alpha^{-2} \)
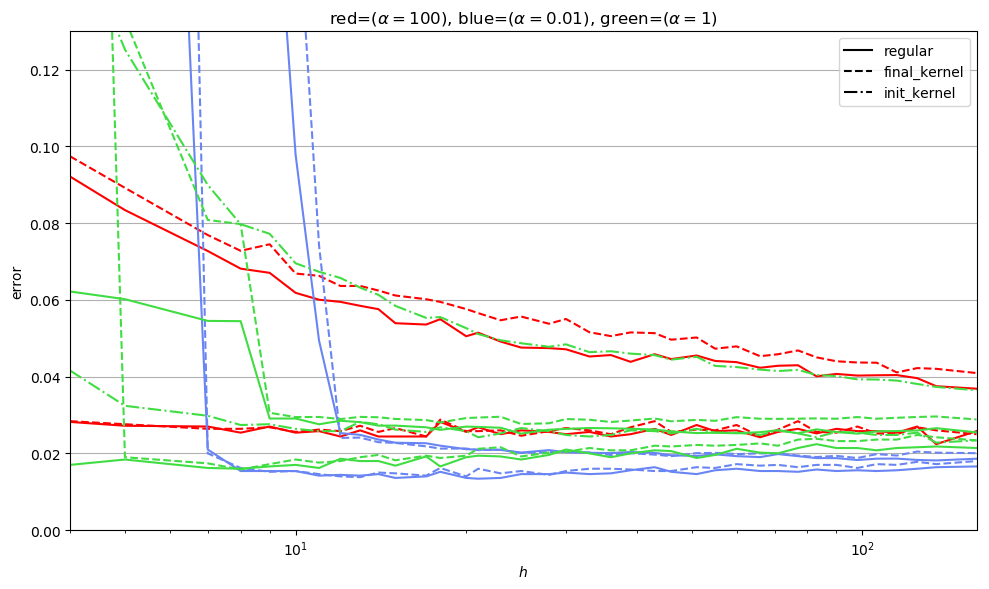
Training \(\alpha (f - f_0)\) allow to control the evolution of the kernel \((\partial f)^2\)
In the limit of small evolution of the parameters

\(\alpha \to \infty\) gives the initial kernel
Architecture: Fully connected
Dataset: 10 PCA of MNIST
\(\alpha (f - f_0)\)
too large LR
CNN