Changepoints in the wild

Martin Tveten

Norweigan Computing Center

IT system monitoring

IT system

Node1

Node2

Node3

Node999

Metric1

Metric2

Metric3

Metric4

Metric5

Metric6

Metric2345

Data

Metric2346

Metric2347

No training labels

!

Sampling rate: 1 minute

!

Stream processing

!

!

Many variables

!

Many systems

Node1

!

Trends and seasonality

!

Missing data

Node2

!

Discrete and continuous distributions

!

Noiseless signals

Node3

!

Outliers

!

Discrete and continuous distributions

Node4

?

!

Solution

1. Run streaming change detection

2. Anomaly detection on segment parameters

Change detector

test = CUSUM()
detector = WindowSegmentor(
  	test, 
  	min_window=4, 
  	max_window=50
)
cpts = []
for t, x in iter_pandas(df):
    detector.update(x)
    if detector.change_detected:
        cpts.append(t-detector.changepoints)
\text{test}_{s:e} = \underset{s \leq k < e}{\max} T(x_{s:k}, x_{k+1:e})

Fang, X., Li, J., & Siegmund, D. (2020). Segmentation and estimation of change-point models: false positive control and confidence regions. The Annals of Statistics, 48(3), 1615-1647.
 

Anomalous segment parameters

Overheating detection in ship engines

Problem

Challenges:

  1. A single observed fault

  2. A lot of data

  3. Continuous monitoring

  4. Simple implementation

  5. False alarms costly 

 

Question:

Can overheating events be timely and reliably be predicted?

Data

12 engines with sampling rate every second over 80-294 days.

Solution

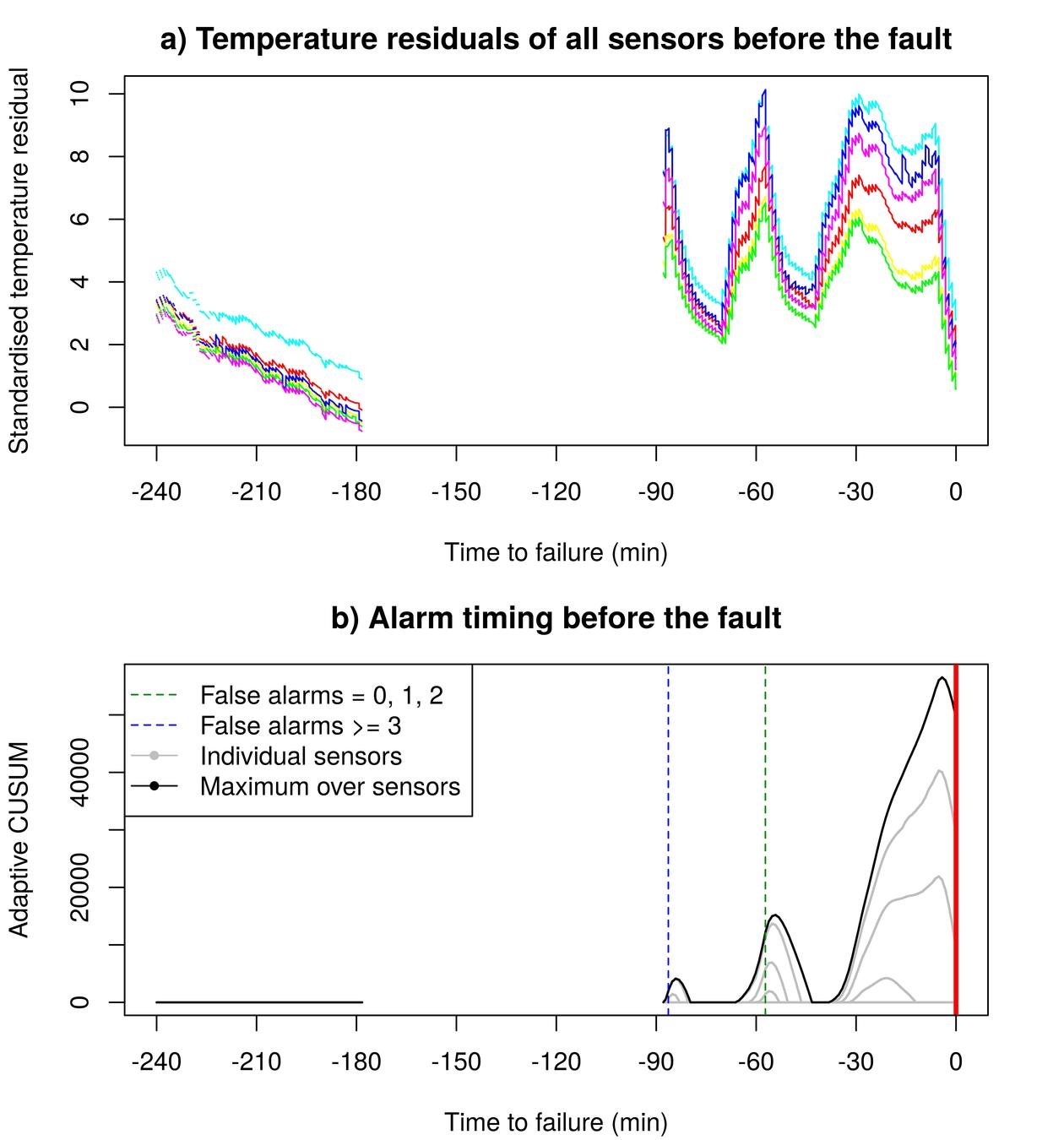
1. Predict temperature from operational variables.

2. Monitor six series of residuals for large positive changes in the mean.

Details?

An adaptive Page-CUSUM test

Lorden and Pollak (2008); Liu, Zhang and Mei (2017)​

1) O(1) computation per step.

2) Only positive changes.

3) Adapts to size of change.

4) Filters out uninterstingly small changes.

\max_j z_{j, t} > b
z_{j, t} = \max \left(0, z_{j, t-1} + \hat{\mu}_{j, t}e_{j, t} - \frac{1}{2}\hat{\mu}_{j, t}^2\right)
\hat{\mu}_{j, t} = \max \left( \frac{s_{j, t}}{n_{j, t}}, \rho \right), \; s_{j, t} = s_{j, t-1} + e_{j, t-1} \text{ if } z_{j, t-1} > 0 \text{ else } 0

Alarm

Test per sensor

Recursive mean

Properties

Tuning

\hat{\rho}(m) = \min \Big\{\rho : \underset{\rho > 0}{\max} \{T(\rho, m)\} - T(\rho, m) \leq \delta \Big\}
b(\hat{\rho}, m)

Number of false alarms in training data

Alarm timing before the true fault

Tolerated loss in detection speed

Extra challenge: Model drift

Anomaly detection in hydro (and wind) power plants

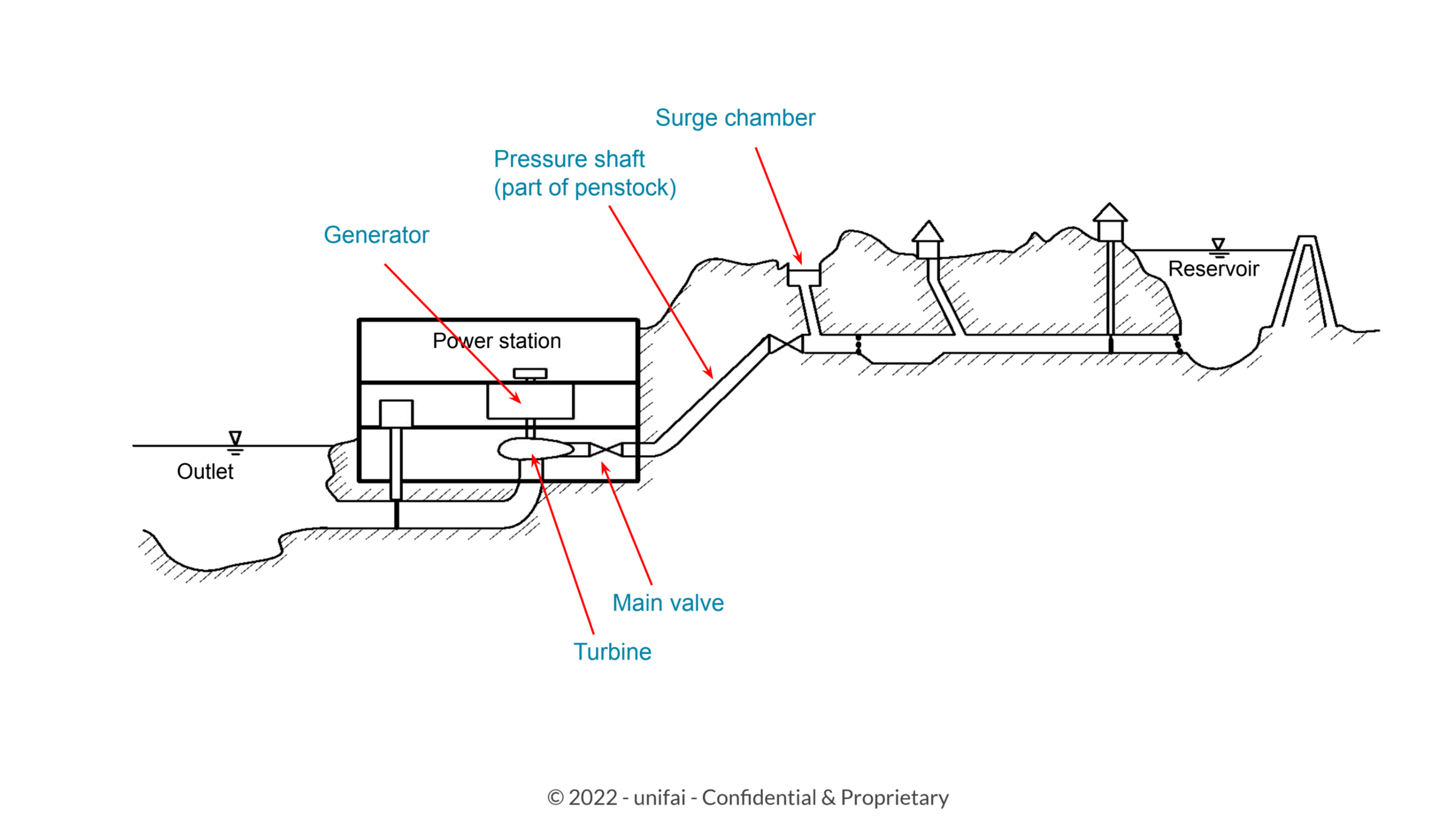
Challenges

1. Data size: 100s of GB.

2. Sampling rate: 5 seconds.

3. Uneven spacing.

4. Missing data.

5. What is the signature of an anomaly?

6. Are there unforeseen data or model drifts?

7. Getting labels to validate methods.

Initial solution: Same procedure

1. Predict variables of interest from operational variables.

2. Monitor residuals for changes = anomalies.

Monitoring technical rooms by sound sensors

Challenges

1. Robust model of what is "normal sound".

2. What is "normal" changes over time.

    a) Have all operational modes been observed?

    b) How should normal model be updated                 while not masking true anomalies?

3. ... <Long list of practical challenges>.

Initial solution: Same framework??

1. Predict variables of interest from operational variables.

2. Monitor residuals for changes = anomalies.

Conclusion

Change detection in streaming data = very useful

Changepoints in the wild

Martin Tveten

Norweigan Computing Center

Made with Slides.com