圖論
基礎名詞解釋
什麼是圖 ?

什麼是圖 ?

什麼是圖 ?
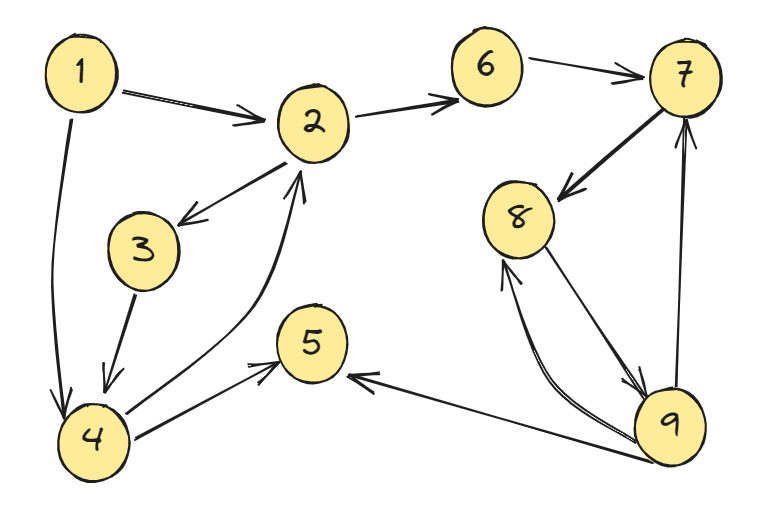
由點(vertices)與邊(edge)構成
好多名詞
點
邊
無向圖
有向圖
帶權圖
無權圖
環
自環
重邊
簡單圖
連通塊
DAG(有向無環圖)
好多名詞
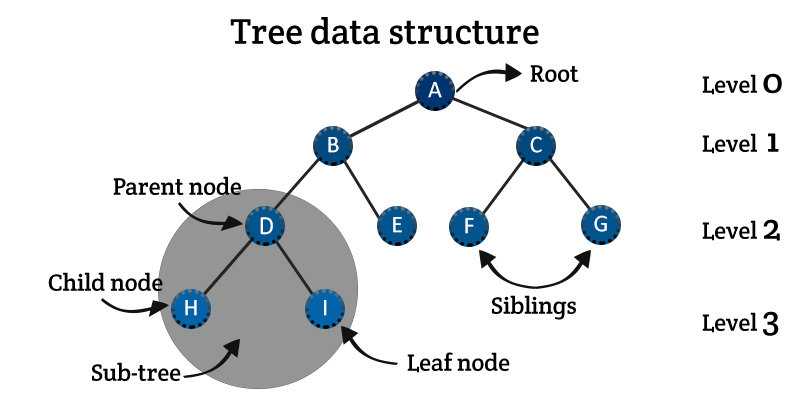
tree : 無向無環圖
如何存一張圖 ?
方法一 鄰接矩陣
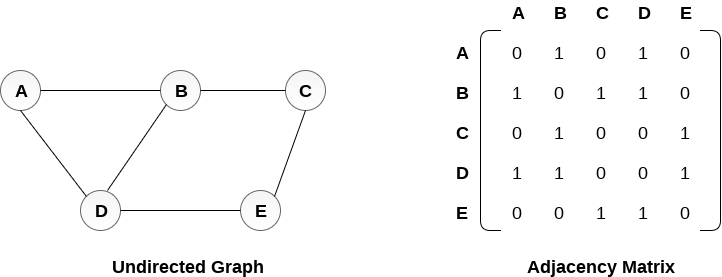
用一個矩陣來存邊
若 (i,j) 為 1 ,則有一條邊連接i、j兩點
優點:
適合存很稠密的圖,可以直接查詢是否有此邊
方法一 鄰接矩陣
缺點:
花費 O(n^2) 的空間
如果圖很稀疏,空間幾乎都是白開
bool E[maxn][maxn];
for(int i=1;i<=m;++i){
int u,v; cin>>u>>v;
E[u][v] = 1;
E[v][u] = 1;
}方法二 鄰接陣列
用一陣列存一個點連接到的所有點
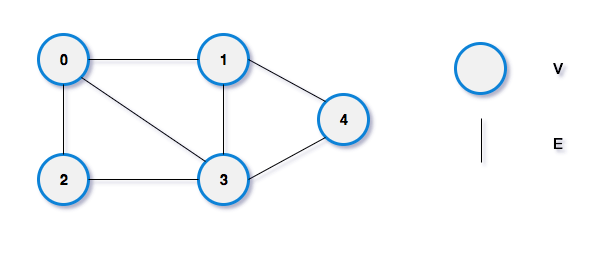
E[0] : {1,2,3}
E[1] : {0,3,4}
E[2] : {0,3}
E[3] : {1,2,4}
E[4] : {1,3}
E[i] : 點 i 連到的所有點
方法二 鄰接陣列
優點 :
花費的空間複雜度是 O(E) (E = 邊數)
方法二 鄰接陣列
優點 :
花費的空間複雜度是 O(E) (E = 邊數)
Text
用鄰接陣列 !
vector<int> E[maxn];
for(int i=1;i<=m;++i){
int u,v; cin>>u>>v;
E[u].push_back(v);
E[v].push_back(u);
} vector<int> E[maxn];
for(int i=1;i<=m;++i){
int u,v; cin>>u>>v;
E[u].push_back(v);
} vector<pair<int,int>> E[maxn];
for(int i=1;i<=m;++i){
int u,v,w; cin>>u>>v>>w;
E[a].push_back({b,w});
} vector<pair<int,int>> E[maxn];
for(int i=1;i<=m;++i){
int u,v,w; cin>>u>>v>>w;
E[a].push_back({b,w});
E[b].push_back({a,w});
}無向無權
有向無權
有向有權
無向有權
BFS
廣度優先搜尋法
BFS是一種可以遍歷整張圖的方法
然後是以廣度優先
也就是他會走得比較,廣



實作
會用一個 queue 來實作
因為 queue 的性質是先進先出
實作
會用一個 queue 來實作
因為 queue 的性質是先進先出
先將起點放入queue中
實作
會用一個 queue 來實作
因為 queue 的性質是先進先出
先將起點放入queue中
接下來每次取出一點,並延伸將所有未造訪節點加入queue
BFS 可以在無權圖中找最短路徑
BFS 可以在無權圖中找最短路徑
因為每次拿出的點,一定是目前可延伸的點中
距離原點最短的那個
code : 無向無權圖
void bfs(int s){
for(int i=1;i<=n;++i) dis[i] = inf;
dis[s] = 0;
queue<int> Q; Q.push(s);
while(!Q.empty()){
int x = Q.front(); Q.pop();
for(int i:E[x]){
if(dis[i] != inf) continue;
Q.push(i);
dis[i] = dis[x] + 1;
}
}
}
DFS
深度優先搜尋法
DFS也是一種可以遍歷整張圖的方法
然後是以深度優先
DFS也是一種可以遍歷整張圖的方法
然後是以深度優先
可以想像成是一走就要走到底為止












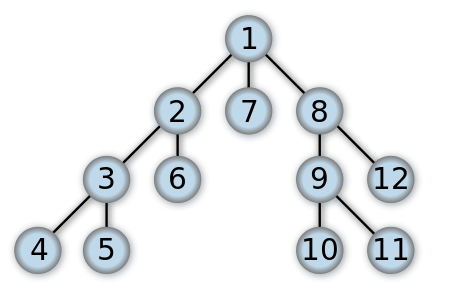
然後有時候我們會記錄下來dfs走到每個點的時間,叫做dfs序
然後有時候我們會記錄下來dfs走到每個點的時間,叫做dfs序
前序就是紀錄進入這個點的時間
後序就是紀錄離開這個點的時間

想這張圖的點編號剛好就是前序
int vi[maxn],dfn[maxn],timer;
vector<int> E[maxn];
void dfs(int x){
dfn[x] = ++timer;
vi[x] = 1;
for(int i:E[x]){
if(!vi[x]) dfs(i);
}
}可以幹嘛?
可以幹嘛?
遍歷一張連通圖、比BFS好寫
可以幹嘛?
遍歷一張連通圖、比BFS好寫
基礎DFS+BFS例題
給一張網格圖,有空地跟牆壁,問有幾塊空地
(連通的空地)
########
#..#...#
####.#.#
#..#...#
########給一張網格圖,有空地跟牆壁,問有幾塊空地
(連通的空地)
########
#..#...#
####.#.#
#..#...#
########有三塊空地
這題BFS、DFS都可以做,只需要可以遍歷一張連通圖即可
code
#include<bits/stdc++.h>
using namespace std;
#define maxn 1005
int n,m,g[maxn][maxn],as;
char c;
void dfs(int x,int y){
if(g[x+1][y]) {g[x+1][y] = 0; dfs(x+1,y);}
if(g[x-1][y]) {g[x-1][y] = 0; dfs(x-1,y);}
if(g[x][y+1]) {g[x][y+1] = 0; dfs(x,y+1);}
if(g[x][y-1]) {g[x][y-1] = 0; dfs(x,y-1);}
}
int main(){
cin>>n>>m;
for(int i=1;i<=n;++i){
for(int k=1;k<=m;++k){
cin>>c;
if(c=='#') g[i][k] = 0;
else g[i][k] = 1;
}
}
for(int i=1;i<=n;++i)for(int k=1;k<=m;++k){
if(g[i][k]) {as++;dfs(i,k);}
}
cout<<as;
return 0;
}給一張網格圖,有空地跟牆壁,以及一起點一終點
求出最短路徑長度、一個解(走法)
給一張網格圖,有空地跟牆壁,以及一起點一終點
求出最短路徑長度、一個解(走法),或是輸出無解
########
#.A#...#
#.##.#B#
#......#
########
9
LDDRRRRRU沒有邊權的最短路徑,就要想到BFS !
因此最短路徑長度就解決了!
那要如何求出一組解呢 ?
如何求出一組解 ?
紀錄一個pre陣列,記錄一個點是從哪裡走來的
ex :
########
#.A#...#
#.##.#B#
#......#
########
pre[2][2] = {2,3}
pre[3][2] = {3,2}
如何求出一組解 ?
紀錄一個pre陣列,記錄一個點是從哪裡走來的
有了這個陣列後,我們就可以從中點,
一步一步回朔回起點
code
#include<bits/stdc++.h>
using namespace std;
#define maxn 1005
int n,m,g[maxn][maxn],d[maxn][maxn],di[2][4] = {{-1,+1,0,0},{0,0,-1,1}};
queue<pair<int,int>> Q;
pair<int,int> start,endd,pre[maxn][maxn];
char c;
bool flag;
void bfs(){
while(!Q.empty()){
auto node = Q.front(); Q.pop();
int x = node.first,y = node.second;
if(x==endd.first&&y==endd.second) {flag=true;break;}
for(int i=0;i<4;++i){
if(d[x+di[0][i]][y+di[1][i]]==1e9) {
Q.push({x+di[0][i],y+di[1][i]});
d[x+di[0][i]][y+di[1][i]] = d[x][y]+1;
pre[x+di[0][i]][y+di[1][i]] = {x,y};
}
}
}
}
void print(int x,int y){
if(pre[x][y]!=start) print(pre[x][y].first,pre[x][y].second);
if(x==pre[x][y].first+1) cout<<'D';
if(x==pre[x][y].first-1) cout<<'U';
if(y==pre[x][y].second+1)cout<<'R';
if(y==pre[x][y].second-1)cout<<'L';
}
int main(){
cin>>n>>m;
for(int i=1;i<=n;++i)for(int k=1;k<=m;++k){
d[i][k] = 1e9;
cin>>c;
if(c=='#') {g[i][k] = 1;d[i][k] = 1e8;}
else g[i][k] = 0;
if(c=='A') start = {i,k};
if(c=='B') endd = {i,k};
}
d[start.first][start.second] = 0;
Q.push({start.first,start.second});
bfs();
if(!flag) cout<<"NO"<<endl;
else{
cout<<"YES"<<endl;
cout<<d[endd.first][endd.second]<<endl;
print(endd.first,endd.second);
}
return 0;
}給一張n點m邊的無向圖
要求最少需要多連幾條邊
才可讓整張圖連通
以及輸出一組解
所以只需要知道有哪些連通快,
再把他們接起來即可
code
#include<bits/stdc++.h>
using namespace std;
#define maxn 100005
int n,m,cc[maxn],t;
vector<int> E[maxn];
vector<int> as;
bool vi[maxn],vicc[maxn];
void dfs(int x){
cc[x] = t;
vi[x] = true;
for(auto i:E[x]){
if(vi[i])continue;
dfs(i);
}
}
int main(){
cin>>n>>m;
for(int i=0;i<m;++i){
int v,u; cin>>v>>u;
E[u].push_back(v);
E[v].push_back(u);
}
for(int i=1;i<=n;++i)if(!vi[i]){t++;dfs(i);}
cout<<t-1<<endl;
for(int i=1;i<=n;++i){
if(!vicc[cc[i]]){
vicc[cc[i]] = 1;
as.push_back(i);
}
}
for(int i=0;i<as.size()-1;++i)cout<<as[i]<<' '<<as[i+1]<<endl;
return 0;
}
一張網格地圖中,有牆壁、空地、很多隻怪獸,
以及一個起點
目的是要走到邊界
每一個時間點,你都可以走一步,每隻怪獸也都可以走一步
不能被怪獸吃到 (存在同一個格子)
求出一組解
一張網格地圖中,有牆壁、空地、很多隻怪獸,
以及一個起點
目的是要走到邊界
每一個時間點,你都可以走一步,每隻怪獸也都可以走一步
########
#M..A..#
#.#.M#.#
#M#..#..
#.######5
RRDDR觀察一下會發現,我只需要知道對於每個點
我走到它的最短路長度
以及所有怪物走到它的最短路長度
觀察一下會發現,我只需要知道對於每個點
我走到它的最短路長度
以及所有怪物走到它的最短路長度
我到每一個點的最短路
直接BFS就好
觀察一下會發現,我只需要知道對於每個點
我走到它的最短路長度
以及所有怪物走到它的最短路長度
所有怪獸的最短路徑可以用
多點源BFS
就是一開始把很多個起都放到queue中
#include<bits/stdc++.h>
using namespace std;
#define maxn 1005
#define inf 1000000009
int md[maxn][maxn],n,m,G[maxn][maxn],ad[maxn][maxn];
bool vi[maxn][maxn];
pair<int,int> start,pre[maxn][maxn];
vector<pair<int,int>> vp;
queue<pair<int,int>> Q;
vector<char> vc;
void Mexplor(int x,int y,int d){
if(!vi[x][y]&&x<=n&&x>=1&&y<=m&&y>=1){
vi[x][y] = true;
md[x][y] = d+1;
Q.push({x,y});
}
}
void Mbfs(){
while(!Q.empty()){
auto pos = Q.front(); Q.pop();
int x = pos.first,y = pos.second;
Mexplor(x+1,y,md[x][y]);
Mexplor(x-1,y,md[x][y]);
Mexplor(x,y+1,md[x][y]);
Mexplor(x,y-1,md[x][y]);
}
}
void trace(int x,int y){
if(x==start.first&&y==start.second){
return;
}else{
trace(pre[x][y].first,pre[x][y].second);
}
int dx = x-pre[x][y].first, dy = y-pre[x][y].second;
if(dx==1) vc.push_back('D');
if(dx==-1)vc.push_back('U');
if(dy==1)vc.push_back('R');
if(dy==-1)vc.push_back('L');
}
void Aexplor(int px,int py,int x,int y,int d){
if(!vi[x][y]&&x<=n&&x>=1&&y<=m&&y>=1&&(d+1)<md[x][y]){
vi[x][y] = true;
ad[x][y] = d+1;
pre[x][y] = {px,py};
Q.push({x,y});
}
}
void Abfs(){
while(!Q.empty()){
auto pos = Q.front(); Q.pop();
int x = pos.first, y = pos.second;
Aexplor(x,y,x+1,y,ad[x][y]);
Aexplor(x,y,x-1,y,ad[x][y]);
Aexplor(x,y,x,y+1,ad[x][y]);
Aexplor(x,y,x,y-1,ad[x][y]);
}
}
int main(){
cin>>n>>m;
for(int i=1;i<=n;++i){for(int k=1;k<=m;++k){
md[i][k] = ad[i][k] = inf;
char c; cin>>c;
if(c=='.') G[i][k] = 1;
else if(c=='#'){
G[i][k] = 2;
vi[i][k] = true;
}
else if(c=='A'){
ad[i][k] = 0;
start = {i,k};
G[i][k] = 3;
}
else if(c=='M'){
vi[i][k] = true;
G[i][k] = 3;
Q.push({i,k});
md[i][k] = 0;
}
}
}
Mbfs();
for(int i=1;i<=n;++i){ for(int k=1;k<=m;++k){
vi[i][k] = false;
if(G[i][k]==2||G[i][k]==3) vi[i][k] = true;
}
}
Q.push(start);
Abfs();
// cout<<"A"<<endl;
pair<int,int> gl;
bool possible = false;
for(int i=1;i<=n;++i) if(ad[i][1]!=inf) {possible = true; gl = {i,1};}
for(int i=1;i<=n;++i) if(ad[i][m]!=inf) {possible = true; gl = {i,m};}
for(int i=1;i<=m;++i) if(ad[1][i]!=inf) {possible = true; gl = {1,i};}
for(int i=1;i<=m;++i) if(ad[n][i]!=inf) {possible = true; gl = {n,i};}
if(!possible) cout<<"NO"<<endl;
else{
// cout<<gl.first<<' '<<gl.second<<endl;
trace(gl.first,gl.second);
cout<<"YES"<<endl;
cout<<ad[gl.first][gl.second]<<endl;
for(int i=0;i<vc.size();++i) cout<<vc[i];
cout<<endl;
}
return 0;
}並查集
DSU
一開始有 n 個集合 ,有兩種操作
- 合併a , b 元素所在的集合
- 詢問a, b 是否在同一個集合
對於每一個詢問輸出 YES/NO
我們今天要講的並查集
就可以解決這個問題
我們今天要講的並查集
就可以解決這個問題
最基礎的DSU有兩種功能
1 : 合併兩個集合
2 : 查詢元素所在的集合
我們想像一個集合有一個老大
他是集合的代表
一開始所有人都是自己的老大
(用箭頭指向老大)
合併
當我們想要合併兩個集合
假設是1號所在、2號所在集合
合併
當我們想要合併兩個集合
假設是1號所在、2號所在集合
我們就將1號點的老大
指到2號點的老大
合併
合併
然後可以觀察到指向自己的人,就是老大
假設還要合併
1號所在、4號所在集合
就將1號點的老大
指到4號點的老大
合併
查詢
當我們要查詢一個元素所在的集合(問老大是誰)
我們就從他開始一直走~~到老大的位置
查詢
當我們要查詢一個元素所在的集合(問老大是誰)
我們就從他開始一直走~~到老大的位置
但聰明的你們應該會發現
這樣不是超慢嗎~~
但聰明的你們應該會發現
這樣不是超慢嗎~~
確實,這樣如果他是一條鍊,每次詢問複雜度為O(n)
優化一 : 啟發式合併
我們每次要將a,b兩集合合併時
都將小的集合併入大的集合
優化一 : 啟發式合併
我們每次要將a,b兩集合合併時
都將小的集合併入大的集合
也就是小的集合的老大,指向大的集合的老大
優化一 : 啟發式合併
我們每次要將a,b兩集合合併時
都將小的集合併入大的集合
也就是小的集合的老大,指向大的集合的老大
但 , 這樣能快多少 ?
優化一 : 啟發式合併
我們每次要將a,b兩集合合併時
都將小的集合併入大的集合
也就是小的集合的老大,指向大的集合的老大
但 , 這樣能快多少 ?
詢問的複雜度直接變成 O(log n) !!
優化一 : 啟發式合併
每次將小集合併入大集合
優化一 : 啟發式合併
每次將小集合併入大集合
設 sza 為大集合大小 , szb為小集合大小
有一個性質為 :
優化一 : 啟發式合併
每次將小集合併入大集合
設 sza 為大集合大小 , szb為小集合大小
有一個性質為 :
優化一 : 啟發式合併
詢問的複雜度就是 ds[] 所形成的樹的樹高
優化一 : 啟發式合併
詢問的複雜度就是 ds[] 所形成的樹的樹高
定義 sz[i] 是 i 點的子樹大小
優化一 : 啟發式合併
詢問的複雜度就是 ds[] 所形成的樹的樹高
定義 sz[i] 是 i 點的子樹大小
由於上述性質
我們從根結點,每往上走一步
sz 都至少會是原來的兩倍以上
優化一 : 啟發式合併
詢問的複雜度就是 ds[] 所形成的樹的樹高
定義 sz[i] 是 i 點的子樹大小
由於上述性質
我們從根結點,每往上走一步
sz 都至少會是原來的兩倍以上
因此樹高就會是 O(log n)
優化一 : 路徑壓縮
每次查詢時,我們走過的每一個點
其實他們的老大跟我是一樣的
優化一 : 路徑壓縮
每次查詢時,我們走過的每一個點
其實他們的老大跟我是一樣的
我們不妨在求完老大後
把路徑上的所有人都直接指向老大
優化一 : 路徑壓縮
這樣做後,複雜度會均攤為每次 O(log n)
證明很難,我不會
DSU + 路徑壓縮 -> O(log n)
DSU + 啟發式合併 -> O(log n)
DSU + 啟發式合併 + 路徑壓縮 -> ??
DSU + 路徑壓縮 -> O(log n)
DSU + 啟發式合併 -> O(log n)
DSU + 啟發式合併 + 路徑壓縮 -> O(α n)
實作
實作上,因為所有點都只有一個出度
所以可以直接用一個陣列存
ds[i] = i 點的老大
實作
code
int sz[maxn],n,ds[maxn],m;
void init(){
for(int i=1;i<=n;++i){
ds[i] = i;
sz[i] = 1;
}
}
int findroot(int x){
if(ds[x] == x) return x;
return ds[x] = findroot(ds[x]);
}
void add(int a,int b){
a = findroot(a), b = findroot(b);
if(sz[b] > sz[a]) swap(a,b);
sz[a] += sz[b];
ds[b] = a;
}
最小生成樹
minimum spanning tree
什麼是最小生成樹 ?
生成樹 ?
生成樹是對於一個連通的無向圖
n 點 m 邊
一個邊的子集 E
符合 |E| = n-1
並且不存在環
生成樹 ?
生成樹是對於一個連通的無向圖
n 點 m 邊
一個邊的子集 E
符合 |E| = n-1
並且不存在環
這樣就會是棵連通整個圖的
生成樹
生成樹 ?
簡單講就是保留一些邊
讓剩下來的邊形成一棵n點的樹
最小生成樹 ?
在所有的生成樹中,所選邊權總和最小的
就是最小生成樹 MST
最小生成樹 ?
最小生成樹不一定唯一
最小生成樹 ?
最小生成樹不一定唯一
所有邊權皆不同 -> 唯一
有邊權相同 -> 可能唯一
最小生成樹有幾個性質 :
1 : 一個環上的最大值,必不屬於MST
最小生成樹有幾個性質 :
1 : 一個環上的邊權最大值,必不屬於MST
2 : 一個cut上的最小邊權必屬於MST
要如何求出最小生成樹呢?
要如何求出最小生成樹呢?
最常用的方法是 Kruskal
還有 prim
Kruskal Algorithm
我們利用剛剛所提到的第一個性質:
環上最大邊,必不屬於MST
Kruskal Algorithm
我們將所有邊按照邊權由小排到大
並依序加入至圖中 (一開始圖只有點)
Kruskal Algorithm
我們將所有邊按照邊權由小排到大
並依序加入至圖中 (一開始圖只有點)
接下來分成兩種情況 :
Kruskal Algorithm
case 1:
當這條邊加進圖後,沒有形成環
Kruskal Algorithm
case 1:
當這條邊加進圖後,沒有形成環
直接加入圖中
Kruskal Algorithm
case 1:
當這條邊加進圖後,沒有形成環
直接加入圖中
case 2:
當這條邊加進圖後,形成環
跳過
Kruskal Algorithm
如何判斷case ?
Kruskal Algorithm
如何判斷case ?
並查集!
Kruskal Algorithm
所有邊跑完過後,加入圖的邊就會形成最小生成樹了 !
簡單吧 :)
Kruskal Algorithm
所有邊跑完過後,加入圖的邊就會形成最小生成樹了 !
簡單吧 :)
但...為什麼?
Kruskal Algorithm
由於邊權從小排大,當有一條邊是 case 1 時
我是連接兩點連通塊的最小邊
符合第二個性質
Kruskal Algorithm
由於邊權從小排大,當有一條邊是 case 2 時
他也是那個環中的最大邊
因此我不加入他,符合第一個性質
由於邊權從小排大,當有一條邊是 case 1 時
我是連接兩點連通塊的最小邊
符合第二個性質
Kruskal Algorithm
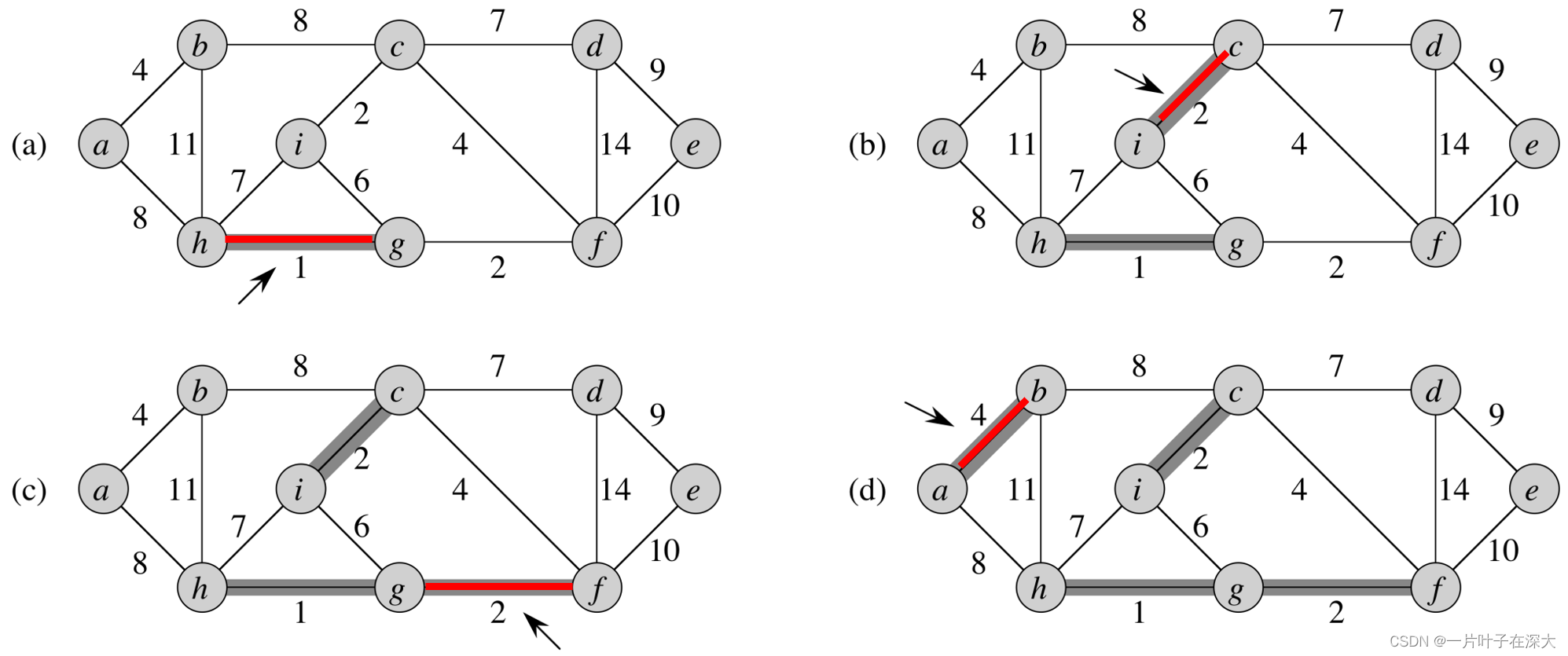
Kruskal Algorithm
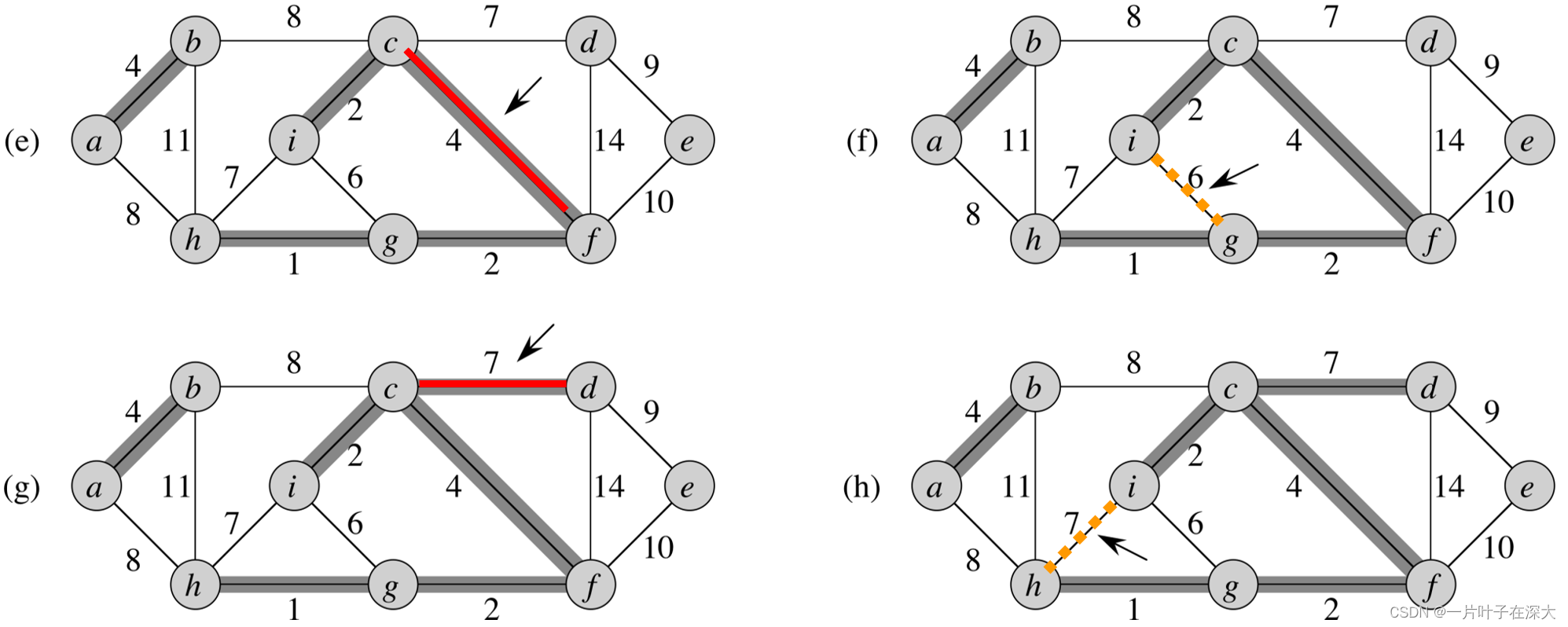
Kruskal Algorithm
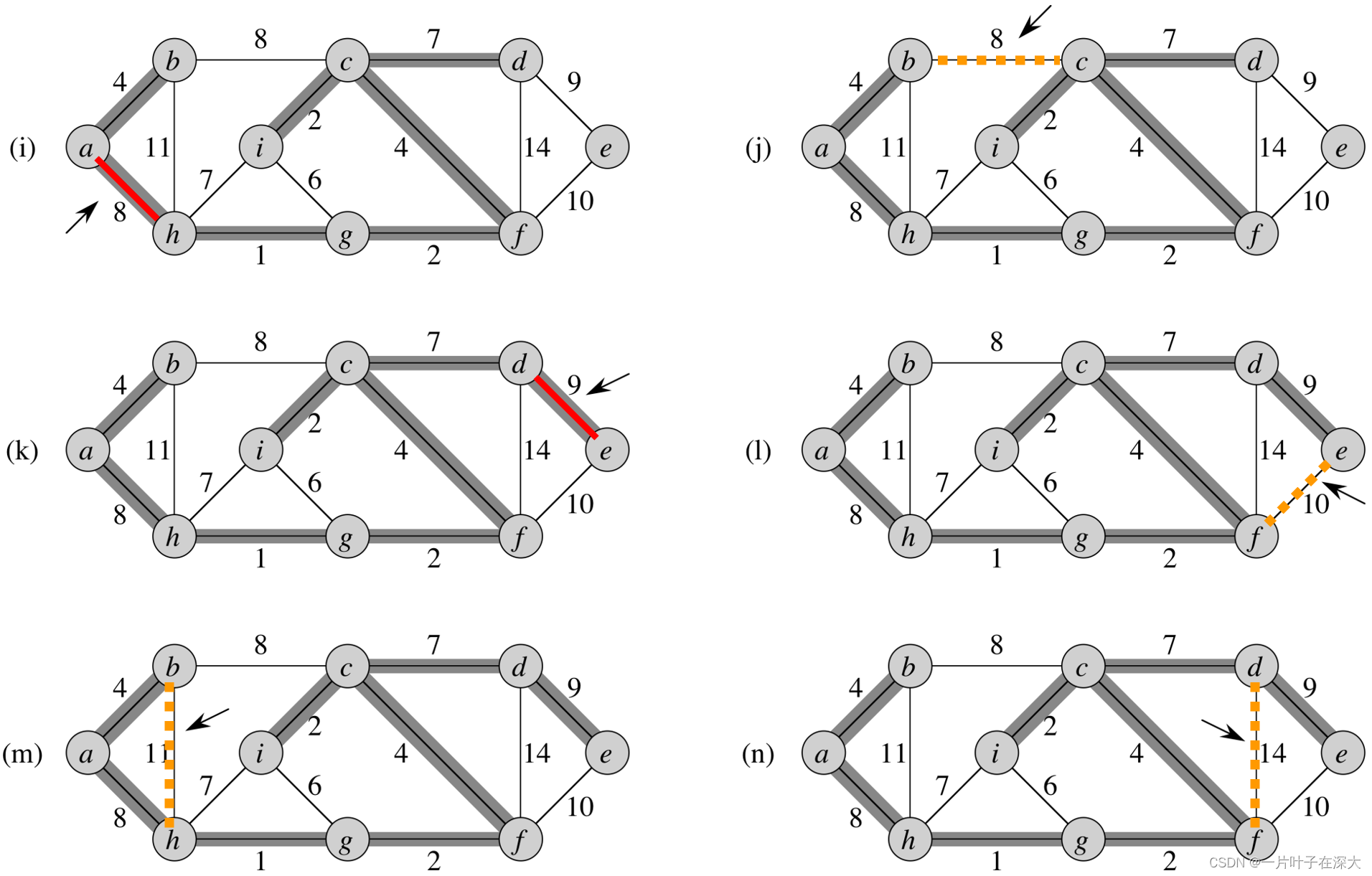
Kruskal Algorithm
時間複雜度:
O(Eα(V))
Kruskal Algorithm
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define maxn 10004
struct ed{
int u,v,w;
};
vector<ed> E;
int ds[maxn];
bool comp(ed a,ed b){
return b.w > a.w;
}
int findroot(int x){
if(ds[x]==x) return x;
return ds[x] = findroot(ds[x]);
}
void add(int a,int b){
ds[findroot(b)] = findroot(a);
}
int n,m;
main(){
cin>>n>>m;
E.clear();
for(int i=0;i<m;++i){
int a,b,c; cin>>a>>b>>c;
E.push_back({a,b,c});
}
for(int i=1;i<=n;++i) ds[i] = i;
sort(E.begin(),E.end(),comp);
int as = 0;
for(int i=0;i<m;++i){
if(findroot(E[i].u) != findroot(E[i].v)){
as += E[i].w;
add(E[i].u,E[i].v);
}
}
cout<<as<<endl;
}prim's Algorithm
我們換個角度來建這棵MST
考慮從一個點開始將MST往外擴張
每次加入一個點
prim's Algorithm
我們每次找到
目前所有MST的點,往外連的邊(連到非MST)中
邊權最小的那個,並將那條邊以及連到的點加入MST
prim's Algorithm
我們每次找到
目前所有MST的點,往外連的邊(連到非MST)中
邊權最小的那個,並將那條邊以及連到的點加入MST
擴張完成後就是最終MST 了
prim's Algorithm
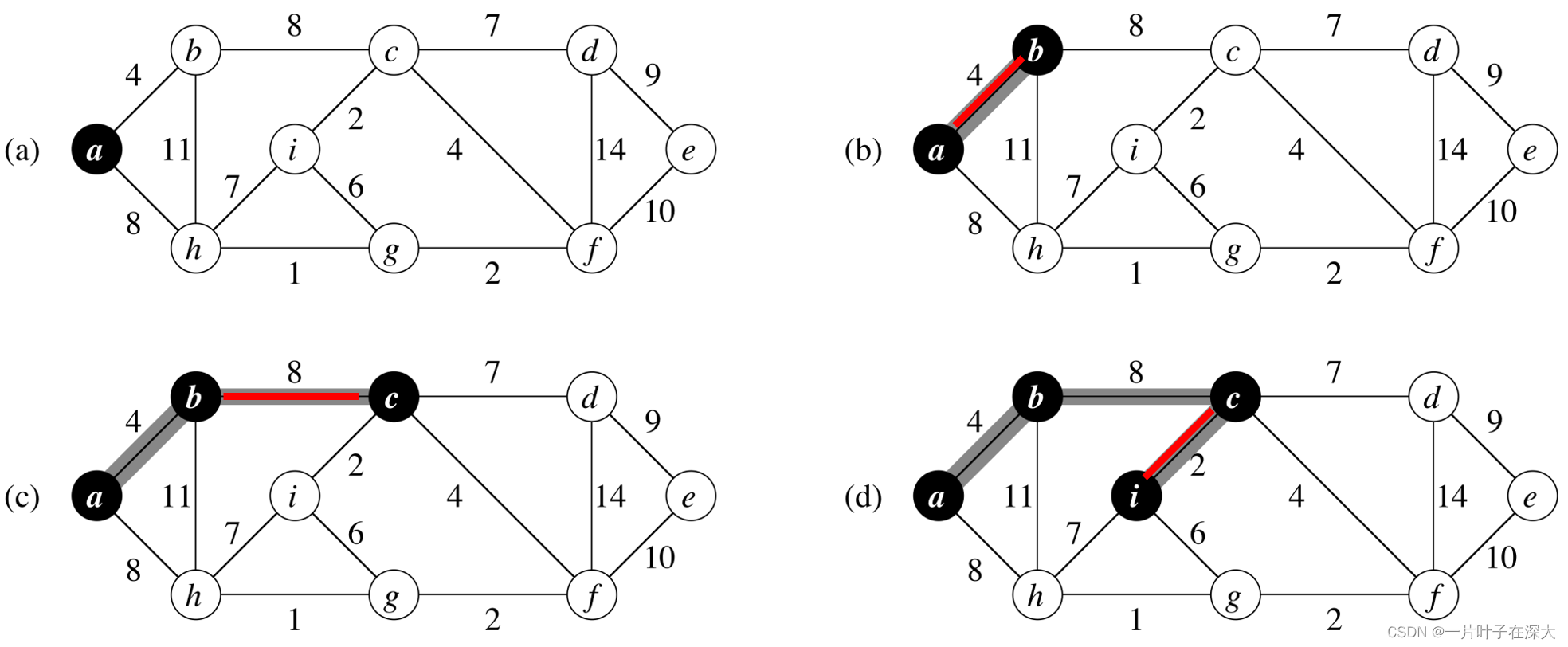
prim's Algorithm
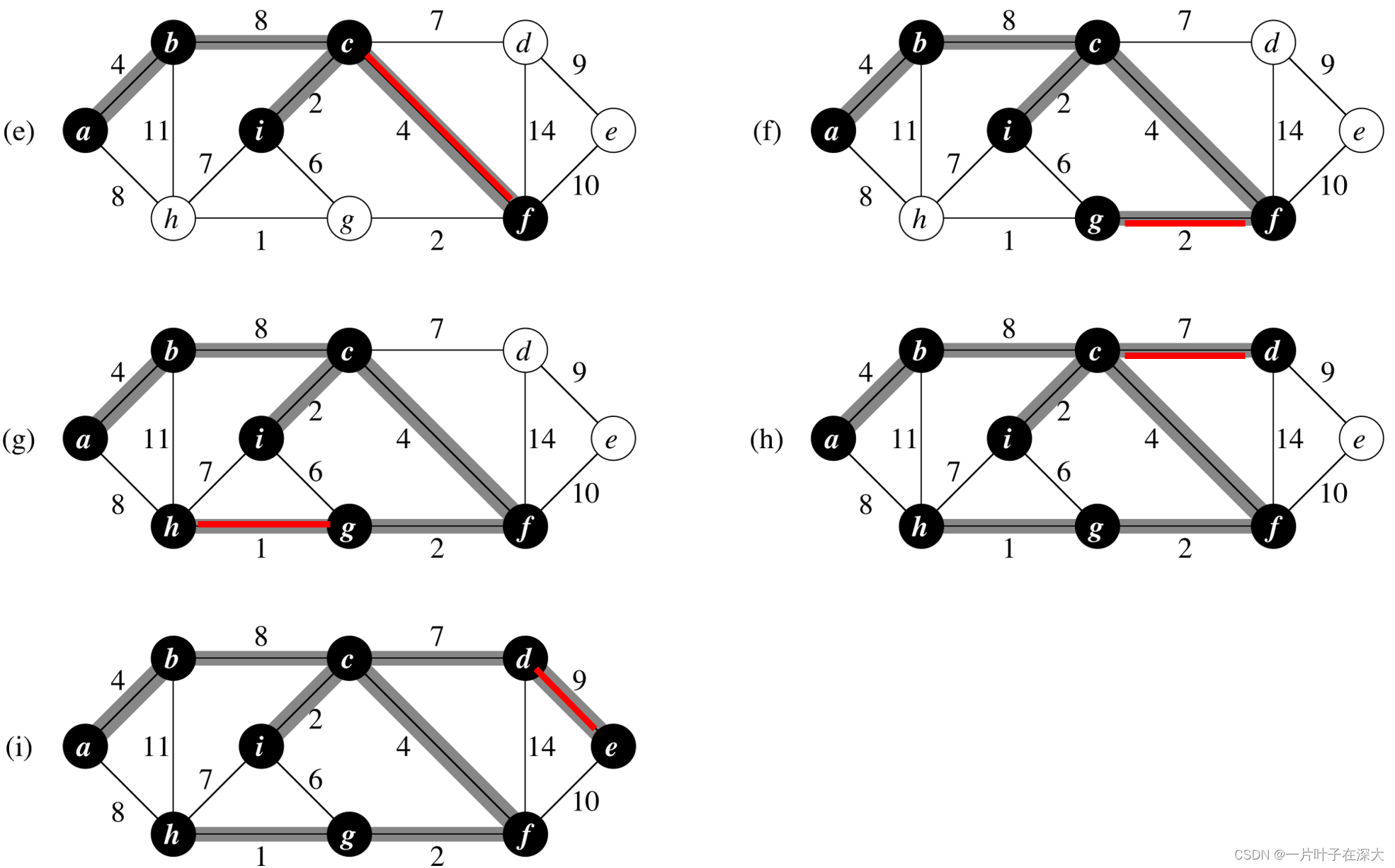
prim's Algorithm
為什麼這樣是對的 ?
prim's Algorithm
為什麼這樣是對的 ?
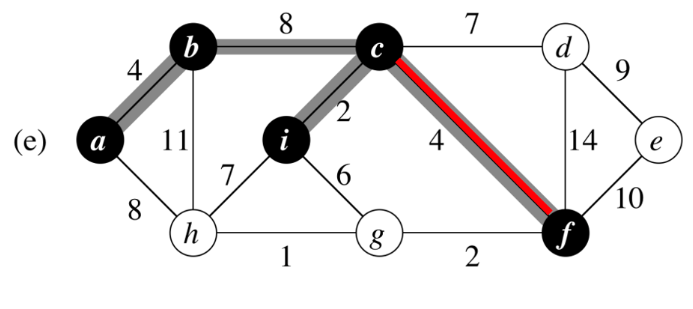
prim's Algorithm
為什麼這樣是對的 ?

性質2 : 一個cut上的最小邊權必屬於MST
prim's Algorithm
時間複雜度會根據實作方式不同而改變:
較常用的有兩種
O(V^2)
O(E + V log V)
prim's Algorithm ( O(E+VlogV) )
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
#define maxn 100005
#define inf 1e18
int n,m;
vector<pair<int,int>> E[maxn];
priority_queue<pair<int,int>,vector<pair<int,int>>,greater<pair<int,int>>> Q;
bitset<maxn> vi;
int primMST(int s){
vi.reset();
Q.push({0,s});
int sum = 0;
while(!Q.empty()){
auto x = Q.top(); Q.pop();
if(vi[x.second]) continue;
sum += x.first;
vi[x.second] = 1;
for(auto i:E[x.second]){
if(!vi[i.first]) Q.push({i.second,i.first});
}
}
if(vi.count() != n) return -1;
return sum;
}
main(){
ios::sync_with_stdio(0); cin.tie(0);
while(cin>>n>>m && n){
for(int i=1;i<=n;++i) E[i].clear();
for(int i=1;i<=m;++i){
int a,b,c; cin>>a>>b>>c;
E[a].push_back({b,c});
E[b].push_back({a,c});
}
cout<<primMST(1)<<endl;
}
}練習題 :
最短路徑
shortest path
這邊所講的最短路徑皆為有邊權的
(無權的直接BFS即可)
首先我們來定義一下最短路徑:
首先我們考慮的是一張簡單無向圖,邊有權重
(有向圖也可)
首先我們來定義一下最短路徑:
定義一條u~v的路徑為,有一長度為K的陣列
符合:
首先我們來定義一下最短路徑:
定義一條u~v的路徑為,有一長度為K的陣列
首先我們來定義一下最短路徑:
定義一條u~v的路徑為,有一長度為K的陣列
定義 u~v 的最短路徑為
所有 u~v 的路徑中,路徑長度最短者
首先我們來定義一下最短路徑:
如果有負環呢?
照樣不就可以一直刷分?
首先我們來定義一下最短路徑:
如果有負環呢?
照樣不就可以一直刷分?
因此我們考慮的圖通常都是沒有負環的
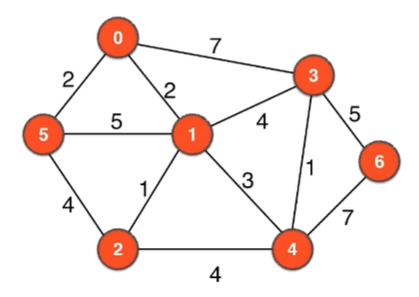
試試看自己手算最短路吧
以下會介紹三個最短路徑算法:
Dijkstra
Bellman-Ford
Floyd Warshall
Dijkstra
這個演算法是以一個 gready 的策略
每次抓出一個已經確定答案的點
來更新其他點
Dijkstra
這個演算法是以一個 gready 的策略
每次抓出一個已經確定答案的點
來更新其他點
這個算法可以求出單個起點至所有點的最短路
稱為單點源最短路
Dijkstra
這個演算法是以一個 gready 的策略
每次抓出一個已經確定答案的點
來更新其他點
此方法有個重要的前提為
沒有負邊
Dijkstra
首先我們定義 dis[i] 是從起點 st 到 i 的最短路徑
我們初始化 :
Dijkstra
我們先將點分成 確定/未確定
代表著 dis[i] 是否為真正的
起點到 i 的最短路徑長度
一開始全部未確定
Dijkstra
我們的策略為 :
- 從未確定中找出目前 dis[x] 最小的點 x
- 將 x 設為確定
- 以 dis[x] 來更新 x 所有鄰居的 dis
Dijkstra
我們的策略為 :
- 從未確定中找出目前 dis[x] 最小的點 x
- 將 x 設為確定
- 以 dis[x] 來更新 x 所有鄰居的 dis
Dijkstra
我們的策略為 :
- 從未確定中找出目前 dis[x] 最小的點 x
- 將 x 設為確定
- 以 dis[x] 來更新 x 所有鄰居的 dis
Dijkstra
我們的策略為 :
- 從未確定中找出目前 dis[x] 最小的點 x
- 將 x 設為確定
- 以 dis[x] 來更新 x 所有鄰居的 dis
以上操作重複 n 輪
所有節點都會變成確定
整張 dis 都會是正確的最短路距離 !
Dijkstra
上面的方法要正確
要必需先證明
從未確定中找出目前 dis[x] 最小的點 x
為什麼貪心地
時 dis[x] 會是正確的
(才能從未確定改成確定)
Dijkstra
當我們選出點 x 時,可以確定
1 : 所有確定點的 dis 都 <= dis[x]
2 : 所有確定點的 dis 都 >= dis[x]
Dijkstra
當我們選出點 x 時,可以確定
1 : 所有確定點的 dis 都 <= dis[x]
2 : 所有確定點的 dis 都 >= dis[x]
在真正的最短路徑中,一定是從某個點走到 x
Dijkstra
當我們選出點 x 時,可以確定
1 : 所有確定點的 dis 都 <= dis[x]
2 : 所有確定點的 dis 都 >= dis[x]
在真正的最短路徑中,一定是從某個點走到 x
如果某點在確定中,則 dis[x] 已經是正確的了
Dijkstra
當我們選出點 x 時,可以確定
1 : 所有確定點的 dis 都 <= dis[x]
2 : 所有確定點的 dis 都 >= dis[x]
在真正的最短路徑中,一定是從某個點走到 x
如果某點在確定中,則 dis[x] 已經是正確的了
如果某點在未確定,則從其走到 x ,更新的距離還是 >= dis[x]
Dijkstra
當我們選出點 x 時,可以確定
1 : 所有確定點的 dis 都 <= dis[x]
2 : 所有確定點的 dis 都 >= dis[x]
在真正的最短路徑中,一定是從某個點走到 x
如果某點在確定中,則 dis[x] 已經是正確的了
如果某點在未確定,則從其走到 x ,更新的距離還是 >= dis[x]
因為沒有負邊!!!!!!
Dijkstra
時間複雜度的部分會因為用不同方式實作
而有不同,這次介紹最常用的
Dijkstra
時間複雜度的部分會因為用不同方式實作
而有不同,這次介紹最常用的
我們將每次從未確定中找出目前 dis[x] 最小的點 x時,使用 priority_queue加速
總時間複雜度為 :
struct comp{
bool operator()(const pair<int,int>&a,const pair<int,int>&b){
return a.second > b.second;
}
};
priority_queue<pair<int,int>,vector<pair<int,int>>,comp> Q;
vector<pair<int,int>> E[maxn];
bitset<maxn> vi;
void dij(int s,int dis[]){
for(int i=1;i<=n;++i) dis[i] = inf;
dis[s] = 0;
Q.push({s,0});
vi.reset();
while(!Q.empty()){
auto x = Q.top(); Q.pop();
if(vi[x.first]) continue;
vi[x.first] = 1;
for(auto i:E[x.first]){
if(vi[i.first]) continue;
if(dis[i.first] > dis[x.first]+i.second){
dis[i.first] = dis[x.first] + i.second;
Q.push({i.first,dis[i.first]});
}
}
}
}這個演算法應該算是最常用的
但在有負邊權時不能用
這個演算法應該算是最常用的
但在有負邊權時不能用
接下來要介紹的都適用負邊
這個算法可以在 O(EV) 時間內找出
單點源最短路
是在有負邊的情況下最快的
這個算法可以在 O(EV) 時間內找出
單點源最短路
是在有負邊的情況下最快的
但他還有一個非常重要的功能是偵測負環
這個算法的核心概念為 :
最短路徑所經過的邊數,最多為 V-1 條
這個算法的核心概念為 :
最短路徑所經過的邊數,最多為 V-1 條
因為如果走了 V 條以上的邊
那一定會出現環,這樣一定是浪費的
(都要最短路了,還繞路)
我們一樣定義 dis[i] 為從起點到 i 的最短距離
並且定義一個操作叫做 relax
我們一樣定義 dis[i] 為從起點到 i 的最短距離
並且定義一個操作叫做 relax
我們對一條從 u 到 v ,邊權為 w 的邊 RELAX :
整個算法的流程就是
每輪操作我們都將所有邊 relax 一次
總共做 V-1 輪,就做完了,耶!!
整個算法的流程就是
每輪操作我們都將所有邊 relax 一次
總共做 V-1 輪,就做完了,耶!!
Text
為什麼這樣是對的?
Text
可以把每一輪操作 (最所有邊 relax)
先假想有一條真正的最短路徑(廢話)
Text
看成是將那條最短路增加一條以上的邊
Text
Text
- 黃色 : 邊權
- 粉紅 : 邊的編號(relax順序)
- 橘色數字 : dis[i]
我們要找從1~5的最短路
Text
Text
- 黃色 : 邊權
- 粉紅 : 邊的編號(relax順序)
- 橘色數字 : dis[i]
經過第一輪relax :
Text
Text
- 黃色 : 邊權
- 粉紅 : 邊的編號(relax順序)
- 橘色數字 : dis[i]
經過第二輪relax :
Text
Text
- 黃色 : 邊權
- 粉紅 : 邊的編號(relax順序)
- 橘色數字 : dis[i]
經過第三輪relax :
接下來不管跑幾輪dis都不會變,就不演示了
Text
Text
每次至少延伸最短路徑中的一條邊:
每次至少延伸最短路徑中的一條邊:
Text
Text
每次至少延伸最短路徑中的一條邊:
Text
Text
每次至少延伸最短路徑中的一條邊:
耶,走到了
Text
Text
如何偵測負環?
如果我們做到第 V 輪relax時,還有某個dis[i] 變小呢
Text
Text
如何偵測負環?
如果我們做到第 V 輪relax時,還有某個dis[i] 變小呢
代表有某條路徑走了某個環之後,
最短路更短了!
Text
Text
for(int i=1;i<=n;++i) d[i] = inf;
d[1]=0;
bool flag,nag = 0;
for(int i=1;i<=n;++i){
flag = false;
for(int k=0;k<m;++k){
if(d[E[k].b] > d[E[k].a] + E[k].x){
flag =true;
d[E[k].b] = d[E[k].a] + E[k].x;
}
}
if(!flag)break;
if(i==n&&flag) nag = true;
}
if(nag) cout<<"有負環 !"<<endl;
else cout<<d[n]<<endl;floyd warshall
Text
Text
這個算法能在 O(V^3) 找出全點對最短路
並且可以有負邊
會用到DP的概念
floyd warshall
Text
Text
大概的想法是,每次多考慮一個點
floyd warshall
Text
Text
大概的想法是,每次多考慮一個點
定義 為從點 i 到點 j,除了這兩點之外,只走 1~ k號點
的最短路
floyd warshall
Text
Text
我們可以列出一個轉移式 :
floyd warshall
我們可以列出一個轉移式 :
將 k 當作中繼點,更新 i 到 j 的距離
每次多考慮一個可以經過的點 (k)
floyd warshall
Text
Text
因此寫成程式大概會長這樣 :
for(int k=1;k<=n;++k){
for(int i=1;i<=n;++i){
for(int j=1;j<=n;++j){
dis[k][i][j] =
min(dis[k][i][j],dis[k-1][i][k]+dis[k-1][k][j]);
}
}
}floyd warshall
Text
Text
然後可以發現空間上可以壓掉一層dp狀態 :
for(int k=1;k<=n;++k){
for(int i=1;i<=n;++i){
for(int j=1;j<=n;++j){
dis[i][j] =
min(dis[i][j],dis[i][k]+dis[k][j]);
}
}
}floyd warshall
跑完這三層迴圈後,整張表格就是全點對最短路了 !
for(int k=1;k<=n;++k){
for(int i=1;i<=n;++i){
for(int j=1;j<=n;++j){
dis[i][j] =
min(dis[i][j],dis[i][k]+dis[k][j]);
}
}
}#include<bits/stdc++.h>
using namespace std;
#define inf 1e18
#define maxn 501
long long n,m,q,dp[maxn][maxn];
int main(){
cin>>n>>m>>q;
for(int i=1;i<=n;++i)for(int k=1;k<=n;++k)if(k!=i)dp[i][k] = inf;
for(int i=0;i<m;++i){
long long u,v,w; cin>>u>>v>>w;
dp[u][v] = min(w,dp[u][v]);
dp[v][u] = min(w,dp[v][u]);
}
for(int k=1;k<=n;++k)for(int i=1;i<=n;++i)for(int j=1;j<=n;++j)
dp[i][j] = min(dp[i][j],dp[i][k]+dp[k][j]);
for(int i=0;i<q;++i){
int u,v; cin>>u>>v;
cout<<((dp[u][v]==inf)?-1:dp[u][v])<<endl;
}
return 0;
}
總結 :
| Dijkstra | Bellman-Ford | Floyd Warshall | |
|---|---|---|---|
| 類型 | 單點源 | 單點源 | 全點對 |
| 時間複雜度(常用) | O((E+V)log(V)) | O(VE) | O(V^3) |
| 限制 | 不能有負邊 | 可以有負邊 | 可以有負邊 |
Bonus
一些額外技巧
什麼 ? Dijkstra的邊權可以亂搞 ?
有些時候,由於題目奇怪的規則,
邊權不是單純的一個數字,
但是其實只要好好的定義,就可以跑Dijkstra!
直接看例題 :)
什麼 ? Dijkstra的邊權可以亂搞 ?
什麼 ? Dijkstra的邊權可以亂搞 ?
邊的權重會隨著時間變化ㄟ,怎麼辦 ?
什麼 ? Dijkstra的邊權可以亂搞 ?
邊的權重會隨著時間變化ㄟ,怎麼辦 ?
但其實有個巧妙的性質
什麼 ? Dijkstra的邊權可以亂搞 ?
邊的權重會隨著時間變化ㄟ,怎麼辦 ?
但其實有個巧妙的性質
當我們專注於要從點 i 走某條邊到點 j
其實我只需要關注,我多快能到達 j
什麼 ? Dijkstra的邊權可以亂搞 ?
當我們專注於要從點 i 走某條邊到點 j
其實我只需要關注,我多快能到達 j
ex :
什麼 ? Dijkstra的邊權可以亂搞 ?
當我們專注於要從點 i 走某條邊到點 j
其實我只需要關注,我多快能到達 j
ex :
像這種情況,可以發現
等到 t=1 再走這條邊
到達 j 的時間是最早的
什麼 ? Dijkstra的邊權可以亂搞 ?
當我們專注於要從點 i 走某條邊到點 j
其實我只需要關注,我多快能到達 j
因此我們就發現可以在固定一點的情況下,
定義邊權為 :
走到這個點的最早時間
什麼 ? Dijkstra的邊權可以亂搞 ?
因此接下來的問題就只剩下
如何快速求出最佳的等待時間
什麼 ? Dijkstra的邊權可以亂搞 ?
我們要在固定 t , D
對於 a >= 0 (等待時間),最小化以下式子
什麼 ? Dijkstra的邊權可以亂搞 ?
先把常數拿掉
什麼 ? Dijkstra的邊權可以亂搞 ?
我們先拿掉下高斯(最後再處理),讓他變成連續的
令
什麼 ? Dijkstra的邊權可以亂搞 ?
因為他只有一個最低點 (凸的),所以可以求
一階導數,然後找到最低點位置
什麼 ? Dijkstra的邊權可以亂搞 ?
因為他只有一個最低點 (凸的),所以可以求
一階導數,然後找到最低點位置
什麼 ? Dijkstra的邊權可以亂搞 ?
令
什麼 ? Dijkstra的邊權可以亂搞 ?
以上的 a 就是最好的等待時間,
但我們將下高斯拿掉了
什麼 ? Dijkstra的邊權可以亂搞 ?
以上的 a 就是最好的等待時間,
但我們將下高斯拿掉了
所以我們就把這個 a 附近幾個數字
都試試看,再取最小即可
什麼 ? Dijkstra的邊權可以亂搞 ?
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define inf 1e18
#define maxn 200005
#define endl '\n'
#define double long double
struct EDG{
int v,c,d;
};
vector<EDG> E[maxn];
int n,m,dis[maxn];
bitset<maxn> vi;
int query(int t,int c,int d){
double tmp = sqrt(d)-1.;
if(tmp < t) return c+(d/(t+1))+t;
int res = inf;
for(int i=tmp-5;i<=tmp+5;++i){
if(i >= t) res = min(res,c+(d/(i+1))+i);
}
return res;
}
void dij(){
for(int i=1;i<=n;++i) dis[i] = inf;
priority_queue<pair<int,int>,vector<pair<int,int>>,greater<pair<int,int>>> Q;
Q.push({0,1});
dis[1] = 0;
while(!Q.empty()){
pair<int,int> x = Q.top(); Q.pop();
if(vi[x.second]) continue;
vi[x.second] = 1;
for(auto i:E[x.second]){
if(vi[i.v]) continue;
int w = query(dis[x.second],i.c,i.d);
if(dis[i.v] > w){
dis[i.v] = w;
Q.push({w,i.v});
}
}
}
}
main(){
ios::sync_with_stdio(0); cin.tie(0);
cin>>n>>m;
for(int i=1;i<=m;++i){
int a,b,c,d; cin>>a>>b>>c>>d;
E[a].push_back({b,c,d});
E[b].push_back({a,c,d});
}
dij();
cout<<(dis[n] == inf ? -1 : dis[n])<<endl;
}
好好利用Floyd Warshall的性質 !
注意到Floyd Warshall
是將可以走的點,從小大到加入考慮
如何利用 ?
好好利用Floyd Warshall的性質 !


好好利用Floyd Warshall的性質 !
才剛剛學過Floyd Warshall的你一下就發現,
當這兩個點連通的瞬間
路徑長就是對應的k !
(k 為目前所考慮到可以走的點)
好好利用Floyd Warshall的性質 !
但是 N = 2000 時
Floyd Warshall O(V^3) 會TLE ㄟ
好好利用Floyd Warshall的性質 !
但是 N = 2000 時
Floyd Warshall O(V^3) 會TLE ㄟ
注意到我們只在乎兩個點何時會連通
(更新到哪個k時)
好好利用Floyd Warshall的性質 !
但是 N = 2000 時
Floyd Warshall O(V^3) 會TLE ㄟ
注意到我們只在乎兩個點何時會連通
(更新到哪個k時)
因此可以 bitset 優化 !
作法直接看 code
好好利用Floyd Warshall的性質 !
#include<bits/stdc++.h>
using namespace std;
using LL = long long;
#define inf 1e18
#define maxn 2005
#define endl '\n'
int n,m,as[40005];
bitset<maxn> bt[maxn];
pair<int,int> p[40005];
main(){
ios::sync_with_stdio(0); cin.tie(0);
cin>>n>>m;
for(int i=1;i<=m;++i){
int a,b; cin>>a>>b;
bt[a][b] = 1;
}
int q; cin>>q;
for(int i=1;i<=q;++i){
int a,b; cin>>a>>b;
p[i] = {a,b};
as[i] = -1;
}
for(int k=1;k<=n;++k){
for(int i=1;i<=n;++i){
if(bt[i][k]) bt[i] |= bt[k];
}
for(int i=1;i<=q;++i){
if(as[i] == -1 && bt[p[i].first][p[i].second])
as[i] = max({p[i].second,p[i].first,k});
}
}
for(int i=1;i<=q;++i) cout<<as[i]<<endl;
}回家練習題 :