deck

枚舉

舉出所有可能一個一個檢查

但要聰明的枚舉，把時間壓到最小

範例

聰明的枚舉 : 找迴文

有一個長度為 n 的字串

請問其中有多少個迴文子字串

有一個長度為 n 的字串

請問其中有多少個迴文子字串

ex :
sdffdw

有一個長度為 n 的字串

請問其中有多少個迴文子字串

ex :
sdffdw

ans : 8個

比較笨的枚舉 :

窮舉所有L R ( 1 <= L < R <=n )

比較笨的枚舉 :

窮舉所有L R ( 1 <= L < R <=n )

對於一組L R，檢查是否為迴文

True : as++

比較笨的枚舉 :

窮舉所有L R ( 1 <= L < R <=n )

對於一組L R，檢查是否為迴文

True : as++

O(n^2)

O(n)

O(n^3)

沒那麼笨的枚舉

提示 : 利用迴文的特性

沒那麼笨的枚舉

提示 : 利用迴文的特性

枚舉回文中點 !!

沒那麼笨的枚舉

提示 : 利用回文的特性

枚舉回文中點 !!

abcddcba

枚舉這個(中心)

枚舉中點 : O(n)

每次擴大一格，最多擴大n/2次 : O(n)

O(n^2)

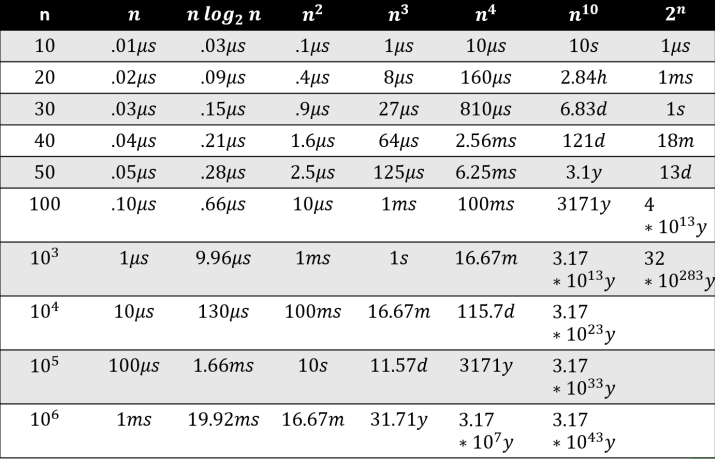
改變枚舉的方法，就可以省非常多時間

開始枚舉各種東西

遞迴枚舉 : Lotto

給你k個數字，印出所有大小為6的子集合

k <= 13

LOTTO

ex:

input : 
2
7 1 2 3 4 5 6 7


ans : 
1 2 3 4 5 6
1 2 3 4 5 7
1 2 3 4 6 7
1 2 3 5 6 7
1 2 4 5 6 7
1 3 4 5 6 7
2 3 4 5 6 7

遞迴枚舉 !

依序決定每個元素是否要拿(遞迴出兩個分支)，並記錄當前拿的數量

#include<bits/stdc++.h>
using namespace std;

int T,k,a;
vector<int> p,ch;
void dfs(int N,int t){
    if(t>6) return;
    if(N==k){
        if(t<6) return;
        for(int i=0;i<ch.size();++i)cout<<ch[i]<<' ';
		cout<<endl;
        return;
    }
    ch.push_back(p[N]);
    dfs(N+1,t+1);
    ch.pop_back();
    dfs(N+1,t);
}
int main(){
    ios::sync_with_stdio(0); cin.tie(0);
    cin>>T;
    while(T--){
        cin>>k;
        p.clear();
        for(int i=0;i<k;++i){
            cin>>a;
            p.push_back(a);
        }
        dfs(0,0);
    }
    return 0;
}

遞迴枚舉 : 八皇后

8 Queens

有一個 8*8的棋盤，有幾種方法能放8個皇后，

並且任兩皇后不可互相攻擊，

請印出所有可能的盤面

8 Queens

有一個 8*8的棋盤，有幾種方法能放8個皇后，

並且任兩皇后不可互相攻擊，

請印出所有可能的盤面

方法一:列出所有可能，一一檢查

方法一(無優化) : 列出所有可能，一一檢查

每個格子有兩種可能

2^64 * 64

方法一:列出所有可能，一一檢查

每個格子有兩種可能

2^64 * 64

TLE

永遠算不完

(檢查時間)

優化一

每橫排最多只能放一個，

因此每舉每橫排Queen的位置，最後檢查

優化一

每橫排最多只能放一個，

因此每舉每橫排Queen的位置，最後檢查

8^8 * 64 少了很多，但還是TLE

優化二

既然我已知我上面的皇后位置 (由上排枚舉至下排)，

那我不是可以不用枚舉上面已經用過的column

優化二

既然我已知我上面的皇后位置 (由上排枚舉至下排)，

那我不是可以不用枚舉上面已經用過的column

ex :

只有勾勾要枚舉

實作上可以用一個陣列紀錄那些column已經被用過

其實優化到這裡，已經可以快速跑完8皇后了 !!

實作上可以用一個陣列紀錄那些column已經被用過

其實優化到這裡，已經可以快速跑完8皇后了 !!

但這時就出現了 n 皇后問題

n <= 15

TLE

優化三

到目前為止，我們已經可以快速檢查column是否被占用，

但檢查斜排還是要花 O(n)時間

如何優化?

優化三

到目前為止，我們已經可以快速檢查column是否被占用，

但檢查斜排還是要花 O(n)時間

如何優化?

觀察看看斜排有什麼性質

只要是左上到右下的斜排，就是x-y相等(y-x也行)

右上到左下的斜排，就是x+y相等

因此也可以快速檢查斜排了 !!

實作可以用陣列，或set(比較慢)

code

(這裡用set，陣列留給你們當練習，記得處理負數)

#include<bits/stdc++.h>
using namespace std;
#define maxn 16

int as,y[maxn],n;
set<int> st1,st2;
void rec(int N){
    if(N==n+1){
        as++;
        return;
    }
    for(int i=1;i<=n;++i){
        if(y[i]) continue;
        if(st1.count(N-i)) continue;
        if(st2.count(N+i)) continue;
        y[i] = 1;
        st1.insert(N-i);
        st2.insert(N+i);
        rec(N+1);
        y[i] = 0;
        st1.erase(N-i);
        st2.erase(N+i);
    }
}
main(){
    cin>>n;
    rec(1);
    cout<<as<<endl;
}

練習題

有障礙的n 皇后問題

其實實作上幾乎一樣

枚舉所有排列

ex :

123

有

123

132

231

213

312

321

這些排法

可以用遞迴的

就是窮舉每一個位置要放誰，做上記號

但c++有內建好用的工具

可以用遞迴的

就是窮舉每一個位置要放誰，做上記號

但c++有內建好用的工具

next_permutation();

可以用遞迴的

就是窮舉每一個位置要放誰，做上記號

但c++有內建好用的工具

next_permutation();

這也是 do while語法唯一的用處

next_permutation(begin,end);

會把目標列迭代成下一個字典序，若已是最大字典序則回傳 false，因此一開始要sort

#include<bits/stdc++.h>
using namespace std;
#define int long long

vector<int> arr;
int n;
main(){
    cin>>n;
    for(int i=1;i<=n;++i){
        int a; cin>>a;
        arr.push_back(a);
    }
    sort(arr.begin(),arr.end());

    do{
        for(int i=0;i<n;++i) cout<<arr[i]<<' ';
        cout<<endl;
    }while(next_permutation(arr.begin(),arr.end()));
}