UNIDAD IV

Programación Funcional

Lenguajes de Programación
Ingeniería en Computación e Informática
Semestre 2019-1

Generadores y decoradores

Generadores

¿Que son los Generadores?

Son una clase especial de funciones que no generan una lista, sino una secuencia de valores sobre el que iterar.
Pueden ser:

Métodos generadores: incluyen la palabra “yield” y se declaran como funciones
Expresión generadora: se declara como listas por comprensión entre “()”

¿Para qué sirven los generadores?

Para generar secuencias en tiempo de ejecución.
Acelerar búsquedas y crear bucles más rápidos.
Mejorar la legibilidad de nuestro código

¿Cómo se construyen los generadores?

Para construir generadores sólo tenemos que usar la orden yield.
Esta orden devolverá un valor y además congelará la ejecución de la función hasta la próxima vez que le pidamos un valor.

Ejemplos (i)

def gen_basico():
    yield "uno"   
    yield "dos"
    yield "tres"


if __name__ == '__main__':
    
    # un bucle
    for g in gen_basico():
        print(g)

    # convertir la generacion en una lista
    print(list(g))

# ejecutar con python3
#~ python gen_1.py

Ejemplos (ii)

def pares():
    index = 1
    # En este caso definimos un bucle infinito
    while True:
        # Devolvemos un valor
        yield index*2
        index = index + 1


if __name__ == '__main__':
    
    # un bucle
    for par in pares():
        print(par)

        # cortamos el bucle para ejemplificar
        if par >= 50:
            break

# ejecutar con python3
#~ python gen_2.py

Ejemplos (iii)

def multiplos_de(n):
    index = 1
    while True:
        yield index*n
        index = index + 1


if __name__ == '__main__':

    # un bucle
    for multiplo in multiplos_de(3):
        print(multiplo)

        # cortamos el bucle para ejemplificar
        if multiplo >= 30:
            break

# ejecutar con python3
#~ python gen_3.py

Ejemplos (iv)

import random

def generador_ips(cantidad):
    for i in range(cantidad):
        a = random.randint(0,255)
        b = random.randint(0,255)
        c = random.randint(0,255)
        d = random.randint(0,255)
        
        yield '{0}.{1}.{2}.{3}' . format(a,b,c,d)


if __name__ == '__main__':
    
    # generar 5 ips
    ips =  generador_ips(5)
    print(list(ips))

# ejecutar con python3
#~ python gen_4.py

Ejercicios en clases

Ejercicio 1

Implementa un generador sucesos (probabilidad) que produce una secuencia infinita de valores booleanos pseudoaletoreos con probabilidad de que sean True. es decir, retornar true si el valor aleatorio es menor a 0.5 y false en caso contrario.

Hint: Utiliza la función random.random () para generar un número pseudo-aleatoreo entre 0.0 y 1.0.

Ejercicios en clases

Ejercicio 2

Implementa un generador de números primos que funcione de la siguiente forma:

for primo in generador_primos(10):
    print primo

Ejercicios en clases

Ejercicio 3

Implementa un generador fibonacci que produce los diferentes de la secuencia de Fibonacci, que tiene la forma:

0, 1, 1, 2, 3, 5, 8, 13, ...

Cuyos dos primeros valores son 0 y 1 por definición y el resto se calculan sumando los dos últimos valores de la sucesión.

Decoradores

¿Que son los decoradores?

Son funciones que reciben una función como parámetro y devuelve otra función.
Cambian el comportamiento de un función, método o clase sin modificar su código.
Crea un “envoltura” alrededor de la función a decorar, esta envoltura y la función original son la nueva función que obtenemos.

Ejemplos

def mi_decorador(funcion):
    def nueva(*args):
        print("Llamada a la funcion", funcion.__name__)
        retorno = funcion(*args)
        return retorno
    return nueva 

@mi_decorador
def mi_fn():
    print(" Hola Mundo ")


if __name__ == '__main__':
    mi_fn()

Patron Memoize

El término "memoization" o "memoize" fue introducido por Donald Michie en el año 1968
El patrón es una técnica utilizada en la computación para acelerar los programas
El patrón memoize consiste en almacenar las soluciones calculadas previamente, para evitar que sean recalculadas, con lo anterior se reduce el tiempo computacional de nuestros algoritmos.
El patrón "memoize" puede ser programada explícitamente por el desarrollador, pero algunos lenguajes de programación como Python proporcionan mecanismos para memorizar automáticamente las funciones (decoradores).

Ejemplo: función fibonacci sin memoize

# Función fibonacci recursiva


def fibonacci(n):
    if n < 2:
        return n
    return fibonacci(n - 1) + fibonacci(n - 2)


f = fibonacci(6)

Ejemplo: árbol de calculo

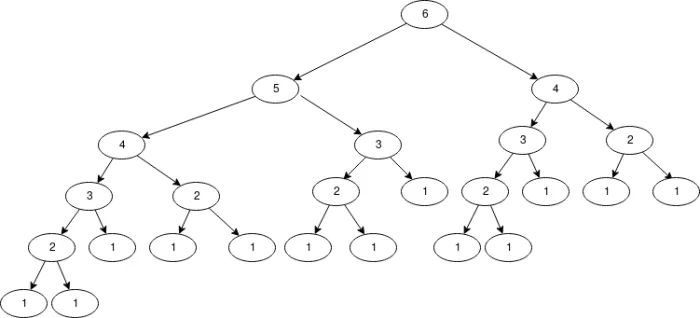
En el árbol de ejecución se producen situaciones donde se realiza el cálculo de algún valor n veces.

Ejemplo: Patrón Memoize

def memoize(f):
    memory = {}

    def wrapper(n):
        if n not in memory:
            memory[n] = f(n)
        return memory[n]
    return wrapper

Ejemplo: Fibonacci con patrón Memoize

def memoize(f):
    memory = {}

    def wrapper(n):
        if n not in memory:
            memory[n] = f(n)
        return memory[n]
    return wrapper



# Utilizando Memoize
@memoize
def fib_memoize(n):
    if n < 2:
        return n
    return fib_memoize(n - 1) + fib_memoize(n - 2)


if __name__ == '__main__':
    fib_memoize(6)

Ejemplo: Fibonacci con patrón Memoize

Se utiliza el decorador construido para utilizar fibonacci con memoización
El patrón a través de los decoradores puede ser aplicado a cualquier función o método de tu proyecto

Actividad en clases

Construya una función que permita calcular n! de forma recursiva. Aplique la memoización en su ejecución.

Solución

#!/usr/bin/env python
# -*- coding: utf-8 -*-


def memoize(f):
    memory = {}

    def wrapper(n):
        if n not in memory:
            memory[n] = f(n)
        return memory[n]
    return wrapper

@memoize
def factorial(k):
    if k < 2: return 1
    return k * factorial(k - 1)


if __name__ == '__main__':
    fact = factorial(5)
    print(fact)

Recursos

https://github.com/mcantillana/generadores_decoradores
https://www.python-course.eu/python3_memoization.php
http://nereida.deioc.ull.es/~lpp/perlexamples/node170.html