Statistical Computing
Instructor: Asst.Prof.Dr. Kürşad Tosun

Prostate Cancer Surgery
Mert Kahyaoğlu 1107090001
Müslüm Ersel Er 1107090003
May 11, 2016
About data
The prostate data frame has 97 rows and 9 columns. A study on 97 men with prostate cancer who were due to receive a radical prostatectomy.
| cavol | weight | age | svi | cp | gleason | pgg45 | bph | psa |
|---|---|---|---|---|---|---|---|---|
|
cancer volume |
prostate weight |
age |
seminal vesicle invasion |
capsular penetration |
Gleason score |
percentage Gleason scores 4 or 5 |
benign prostatic hyperplasia amount |
prostate specific antigen |
Prostate-specific antigen (PSA) is a protein produced by cells of the prostate gland. PSA level in men's blood helps doctors determine whether prostate cancer is present.
Aim of the project
The goal of our project is to determine significant predictor attributes for response value PSA and predict the PSA value for a patient according to given parameters.
Solution Aproach
To achieve our goal, we used several techniques such that;
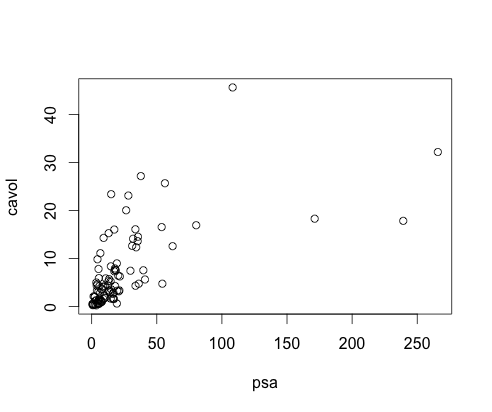
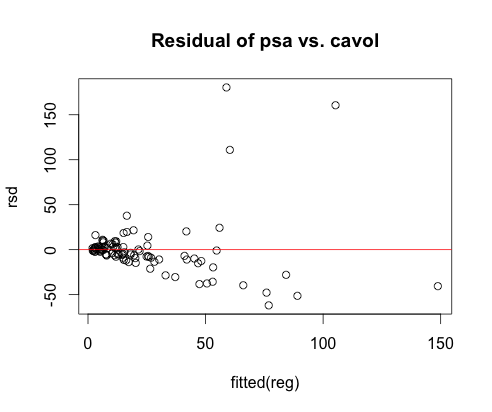
- Fitted a linear model and checked it using scatterplot for correlations and residual plot for linearity.
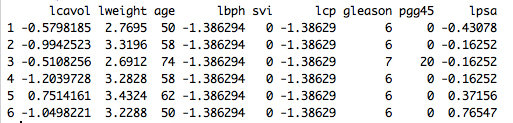
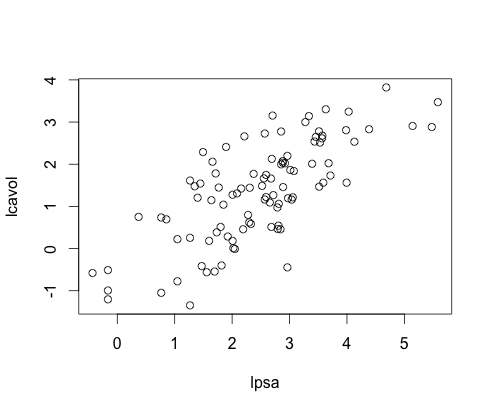
- Transformed our data to log format for better results
- Fitted a linear model and checked it
- Used F-test to specify associated variables
- Generated the least square equation for predictions
- Reduced our model and compared with the previous one using F-test
- Made new predictions and checked the results with the previous one.
Original Data

Logged Data
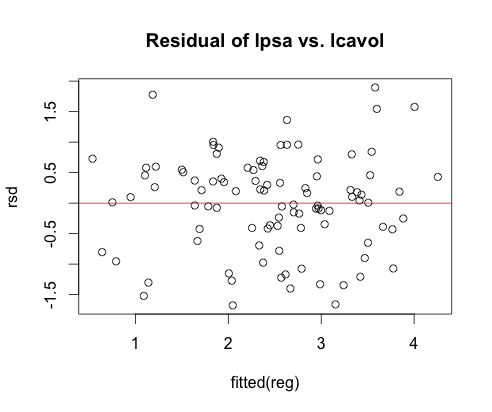
Linear Model (log - full model)

psa: response, others: predictor
Linear Model (Original)

Associated Variables (F-test)
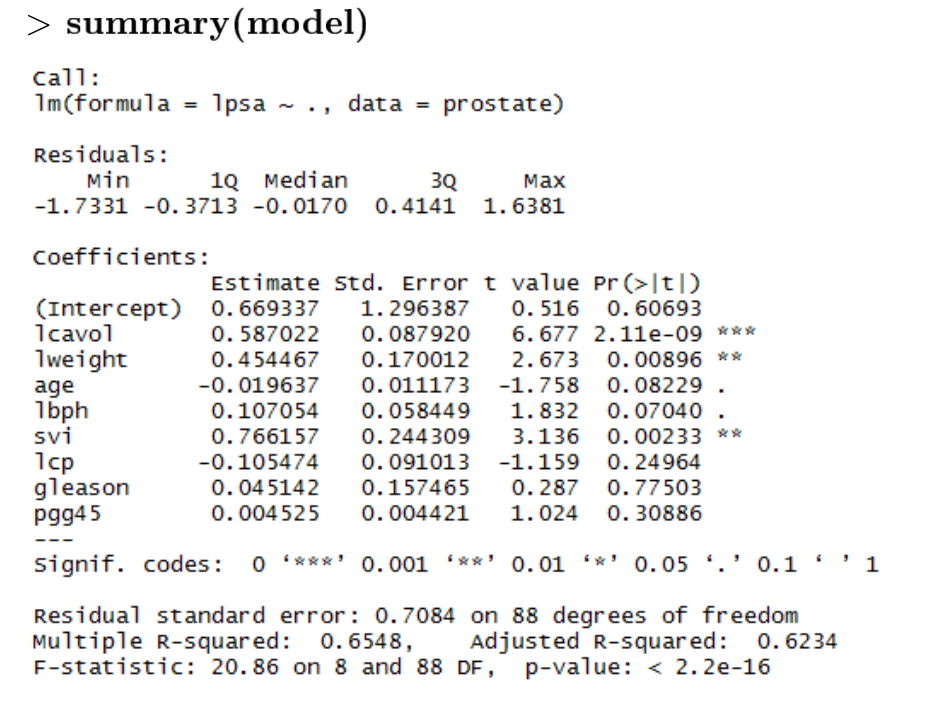
H0: coefficients = 0 means no association
HA: coefficients != 0
Since the p-value=2.2x10−16 < 0.05, reject H0. There is an association between lpsa and other variables which means the model is suitable.
Least Square Equation
By looking at our model, we can create regression equation as follow;
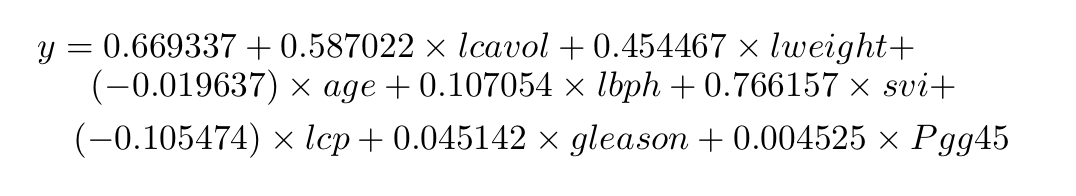

We will use this equation for predictions
Prediction Example
| cavol | weight | age | bph | svi | lcp | gleason | Pgg45 |
|---|---|---|---|---|---|---|---|
| 4.26 | 37.45 | 65 | 1.35 | 0 | 0.45 | 7 | 15 |

Reducing Our Model
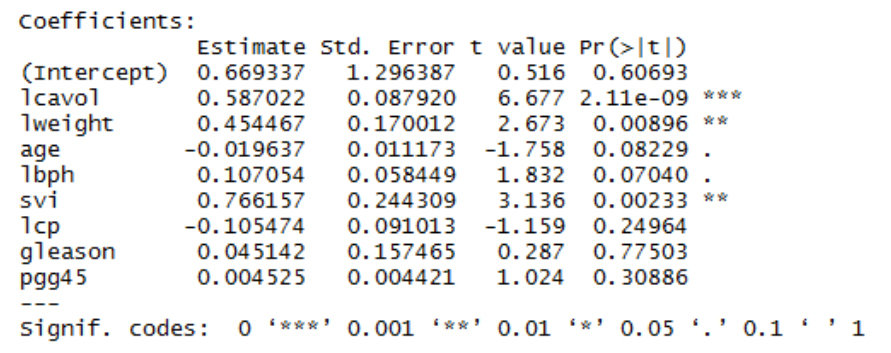
According to F-test, lcavol, lweight and svi are significant on lpsa, the others not. Therefore reduced model will be as follows:
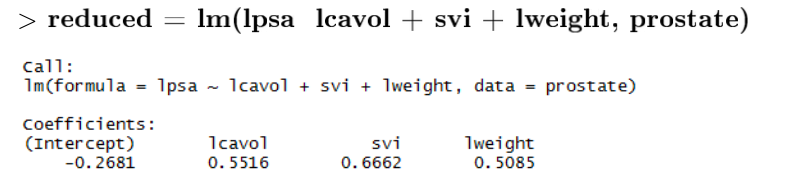
Check Reduced Model

Since p-value=0.2167 is greater than 0.05 we cannot reject the null hypothesis at the 5% level of significance. It appears that the variables age, lbph, lcp, gleason, pgg45 do not contribute significant information to psa.
Final Prediction with Reduced Model
Result is almost same as the full model, therefore reduced model can be used instead.
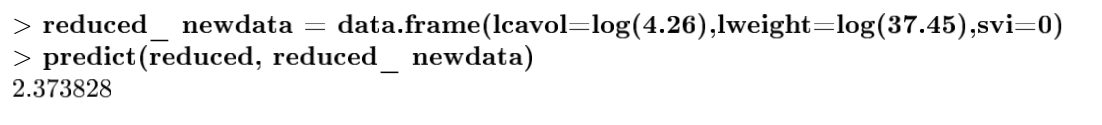
| cavol | weight | svi |
|---|---|---|
| 4.26 | 37.45 | 0 |