Зависимые запросы
и завышенная чувствительность

slabod@, 01.09.2017

Offline-тестирование

Q = (q_1, q_2, \ldots, q_n)
X = (x_1, x_2, \ldots, x_n)
Y = (y_1, y_2, \ldots, y_n)
p_{value}

1

2

3

4

F_X, F_Y

All queries

\frac{\overline{X} \;\; - \;\; \overline{Y}}{\sqrt{\ldots}}

1. Генерация корзины

2. Ранжирование

3. Рассчёт метрики

4. Стат-тест

Зависимость значений метрики

Q = (q_1, q_2, \ldots, q_n)
X = (x_1, x_2, \ldots, x_n)
Y = (y_1, y_2, \ldots, y_n)

1

2-3

All queries

(all possible \(x_i\) values)

\(q_i, q_j\) выбираются равномерно и попарно независимо

\Longrightarrow

Для всех \(i, j\) случайные величины \(x_i, x_j\) независимы

Зависимость \(p_{value}\)

Q_1

1

All queries

(all possible \(p_{value}\) )

В каждом эксперименте

генерируется новая корзина \(Q_i\)

\Longrightarrow

Все \(p_i, p_j\) попарно независимы

Q_2

2-3

X_1,Y_1
X_2,Y_2
p_1
p_2

4

Зависимость \(p_{value}\)

Q

1

2-3

All queries

(all possible \(p_{value}\) )

Реальная ситуация:

единственная корзина на набор экспериментов

\Longrightarrow

Зависимые  \(p_i, p_j\) ?

X_1,Y_1
X_2,Y_2
p_1
p_2

4

Зависимость запросов

Q = (q_1, \ldots, q_n)

1

2-3

All queries

(all possible \(p_{value}\) )

Пусть

\(q_1 = \) "vk.com"

\(q_2 = \) "моя страница"

\Longrightarrow

Значения \(x_1, x_2\) сильно зависимы

X_1,Y_1
X_2,Y_2

4

p_1
p_2

Пусть два эксперимента похоже изменяют качество на кластере "vk.com" и на нескольких других

Вердикт стат-теста про эти эксперименты похож

Нельзя считать значения \(p_i, p_j\) абсолютно независимыми:

\(p_i\) более зависимы, чем при отсутствии кластеров

\Longrightarrow
\Longrightarrow

Основная гипотеза:

Наличие в корзине похожих запросов повышает чувствительность метрик

Mean_{E}[-\ln p_{value}(E)] - 1

Напомним определение чувствительности:

Каждый эксперимент корректен сам по себе,

но их выводы зависимы между собой

Маленькое значение \(p_{value}\) вносит большой вклад в Sensitivity

Эксперименты \(E_1 \: \text{и} \: E_2\) похоже и значительно меняют качество на кластере
\(\Longrightarrow\) их значения \(p_{value}\) вносят большой вклад одновременно

План сравнения чувствительности

  1. Разбить запросы на корзины похожести
     
  2. Вычисление метрики в корзине
     
  3. Линеаризация:
    для каждой группы дополнение до одинакового размера средним значением
     
  4. Сравнение с некластеризованным случаем

Наивная кластеризация

Запросы в одном кластере \(\Longleftrightarrow\) 

у них есть общее слово длины хотя бы 4

Проблема: 

Запросы объединяются в длинные цепочки

\(q_1\) — \(q_2\) — \(\ldots\) — \(q_l\)

длиной до нескоких сотен.

Несколько очень больших групп и много маленьких, сильно падает чувствительность.

Модификация Kruskal's algorithm

Ограничиваем размер кластера!

  • Для всех \(n\) запросов вычисляем попарную похожесть через DSSM
    — скалярное произведение нормированных семантических векторов
  • Перебираем все пары \((q_1, q_2)\) и объединяем пару в один кластер, если размер кластера не превышает \(k\)
Q
d_1
d_2
d_3
d_4

Требование к кластеризации:
Запросы из разных групп должны быть независимы. 

Утверждение:
второй алгоритм минимизирует максимальную похожесть в паре из разных кластеров для всех разбиений с заданным размером кластера \(k\)

Результат кластеризации

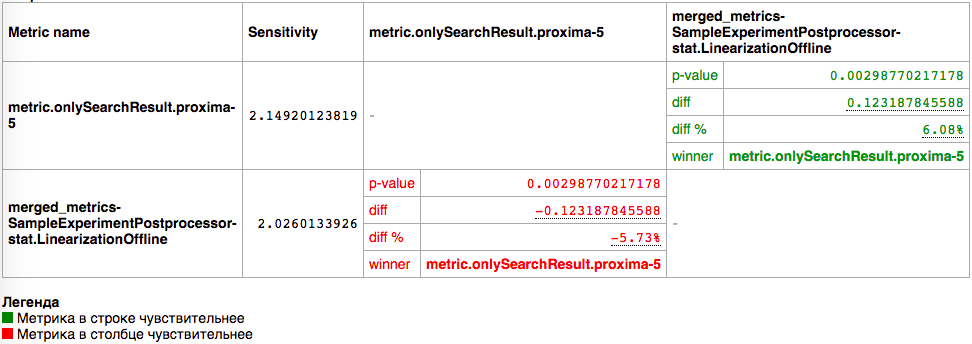
proxima-5

bucketized_
proxima-5

proxima-5

bucketized_
proxima-5

При разбиении на группы размера 0.02 величины корзины разница в чувствительности около 5%

Это статистически значимое падение

Проверка эффекта кластеризации
на чувствительность

  1. Сравнение кластеризации на основе зависимости
    и кластеризации со случайным разбиением
     
  2. Сравнение кластеризации на реальных экспериментах
    и на искусственно сгенерированных данных

Случайные группы

Несколько итераций разбиения запросов на случайные группы с тем же набором размеров, что группы зависимости.

Чувствительность падала статистически незначимо.

Нет оснований отвергнуть предположение "разбиение со случайными группами порождает такую же чувствительность, как отсутствие разбиения".

Синтетические данные

Дано:
\(c_1, c_2, \ldots, c_n\) — контроль
\(e_1, e_2, \ldots, e_n\) — эксперимент

Как сгенерировать синтетические данные, не заботясь о зависимости между \(c_i, e_i\)?

Сгенерируем массив разностей \(c_i - e_i\) !

\mathscr{N}(\mu, \delta) \rightarrow (d_1, d_2, \ldots, d_n)

Синтетические данные

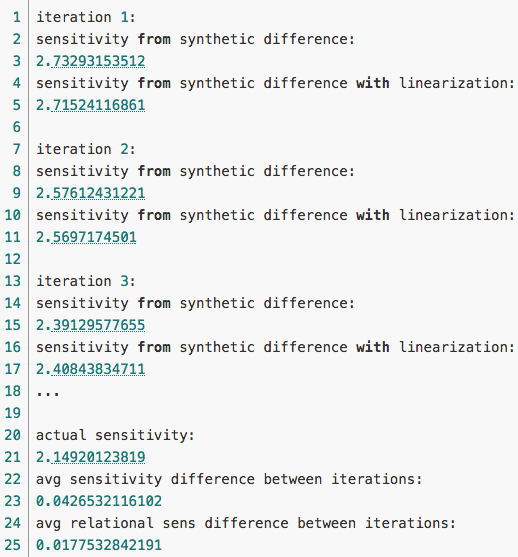
Для искусственных данных среднее относительное понижение чувствительности равно 0.0177

Для реальных данных относительное понижение чувствительности на единственной итерации равно 0.0573

Выводы

  • Разбиение реальных данных на корзины зависимости сильнее понижает чувствительность, чем разбиение сгенерированных синтетических данных
    \(\Longrightarrow\) Без     разбиения для искусственных данных вычисляется ненастоящая, "завышенная" чувствительность.
     
  • Разбиение реальных данных на случайные корзины зависимости не понижает чувствительности
    \(\Longrightarrow\) Mетод разбиения на корзины важен.

Спасибо за внимание! 

Подробности на вики-странице:
https://wiki.yandex-team.ru/users/slabod/dependent-queries/

Made with Slides.com