"Matching Auctions
for Search and Native Ads"
ACM EC’18
Cavallo, Sviridenko, Wilkens
slabod@
MEM-seminar, 02-09.04.2019
Анонс
- Аукционы рекламы
- allocation
- pricing
- Separability нереалистично
- Allocation curves
- SGP- и VCG-цены
- Эффективные алгоритмы
- Две части доклада
Часть 1,
мотивационная
slabod@
MEM-seminar, 02.04.2019
Введение

$$1$$
$$3$$
$$2$$
$$4$$
$$,p_{i_1}$$
$$,p_{i_2}$$
$$,p_{i_3}$$
$$,p_{i_4}$$
$$p_k \le b_k$$
Формализация
- Участники $$i \in $$
- Слоты $$j \in$$
- Вероятность клика
- Utility
- Ожидаемая польза
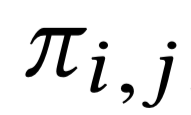
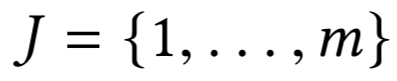
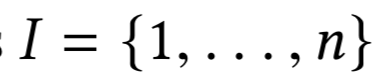
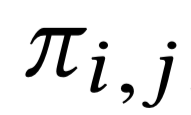
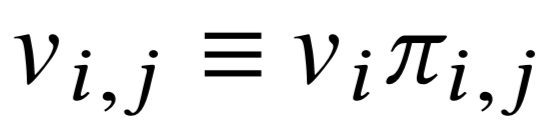
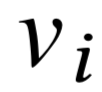
Задача платформы
- Принять ставки \( b_i \longleftrightarrow v_i \)
-
Разместить биддеров по слотам
- Максимизировать SW по \(\sigma:\)
\(\sum\limits_j v_{i, j} \;=\; \sum\limits_j b_{\sigma(j)} \pi_{\sigma(j), j}\) - Определить цены
\(\sigma: J \to I \)
\(\sigma(j) = i \)
Separability
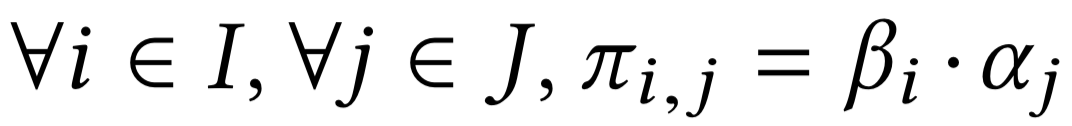


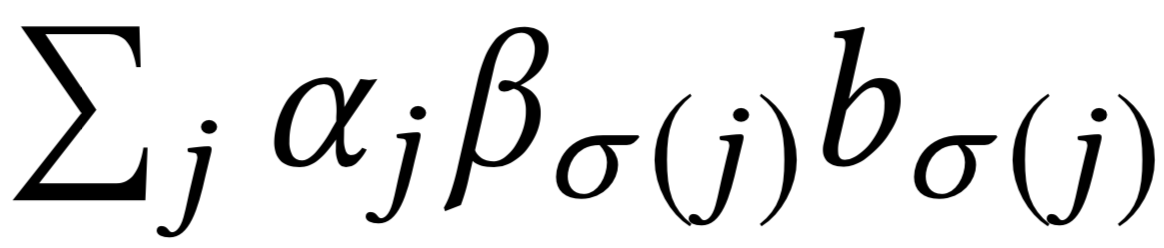

\(\sum_j \pi_{\sigma(j), j} b_{\sigma(j)} \;=\)
\(\sum_i x_i y_i \;\to\; \max\)
ранжирование:
GSP — generalized second price auction
ранжирование:
минимальная возможная для \(\sigma(j)\) для слота \(j\):
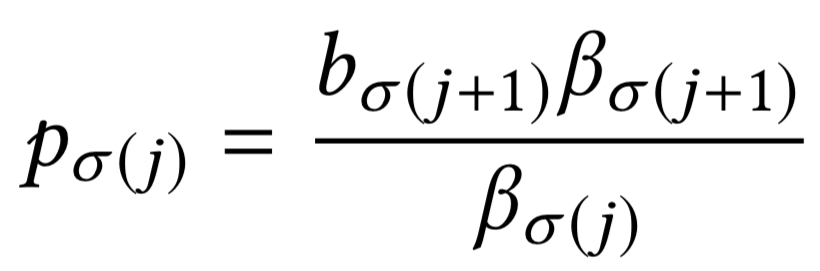
GSP — generalized second price auction
- Существование равновесия
- Легко анализируется и вычисляется
- Separability критична
Нереалистичность separability: native ads
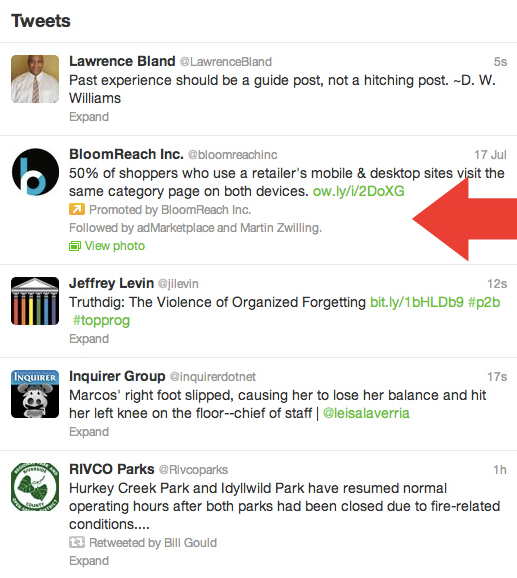
- Внутри контента
- 1 – 2 рекламы на экране
- \(\alpha_j\) — вероятность увидеть слот \(j\)
— уменьшается - \(\beta_i\) зависит от типа рекламы:
- CPM — per-impression, \(\beta_i = 1\)
- CPC — per click, \(\beta_i = Pr[click | view]\)
- conversion / app-installation, \(\beta_i = \,?\)
модель CPM сепарабельна:
\(\pi_{i, j} = \alpha_j\)
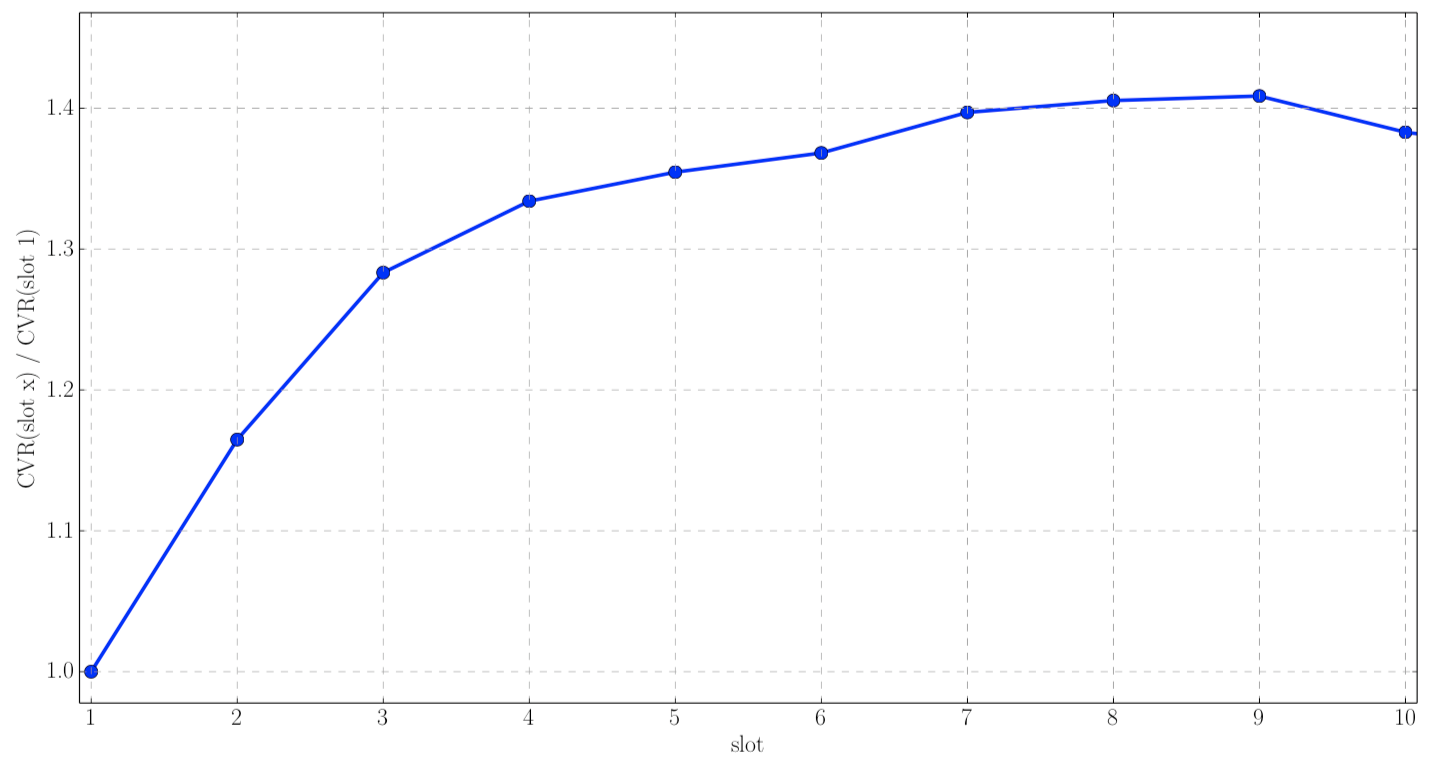
Нереалистичность separability: CPC
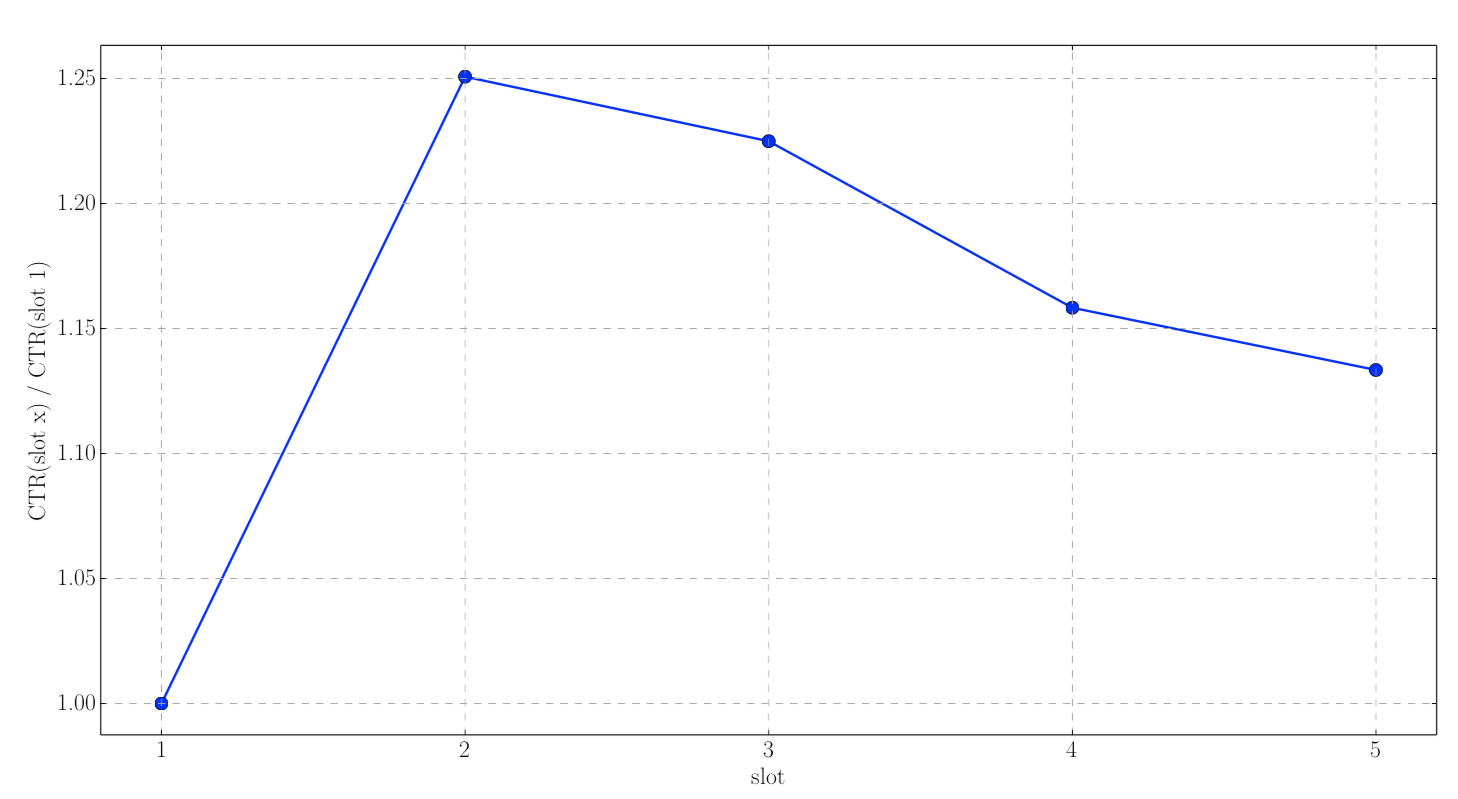
вероятность клика при условии просмотра: Yahoo Native Ads, 17m просмотров
другой смысл \(\alpha_i\), чем для CPM
Нереалистичность separability
- Разные векторы \(\alpha\) для разных моделей?
- Не работает для смешанных моделей
- Реклама в поиске по разному привлекает пользователя в зависимости от слота
Основные вопросы: allocation
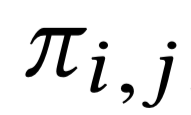
Как определить соответствие bidder — slot без отделимости?
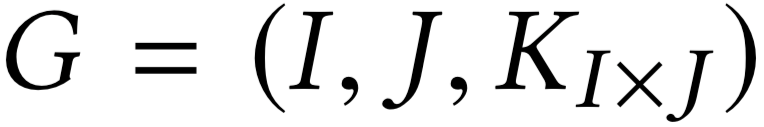
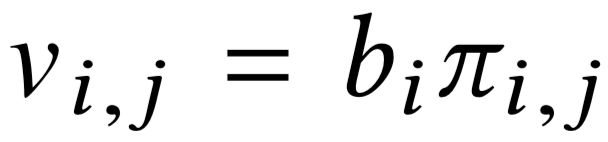
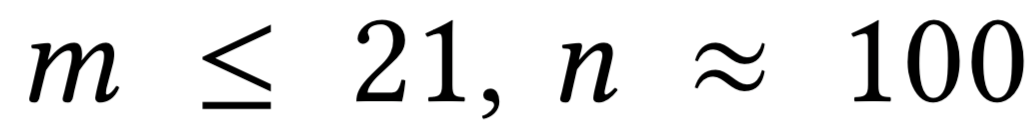
\(\sigma(.):\) \(\sum_j \pi_{\sigma(j), j} b_{\sigma(j)} \; \to \max\)
Hungarian method: \(O(nm^2)\)
time \(\le 1ms\)
Yahoo Native Ads:
Паросочетания!
\(\sigma: J \to I \)
\(\sigma(j) = i \)
Основные вопросы: pricing
Как назначать цены для максимального паросочетания?
- равновесны
- вычислимы
VCG: Vickrey-Clarke-Groves mechanism




VCG: prices
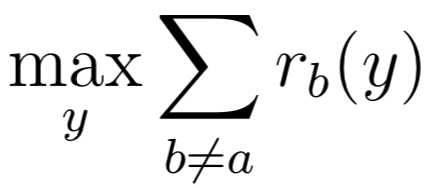
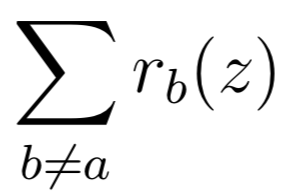
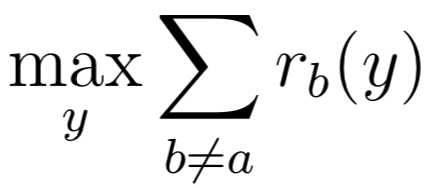
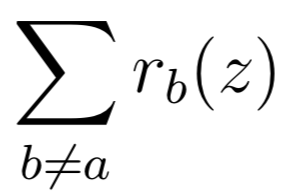

цена

выигрыш \(a:\)
VCG: truthfulness
1. Честный вариант


2. Нечестный вариант
сообщили \(r_a(.) = u_a(.)\)
сообщили \(r'_a(.) \neq u_a(.)\)
VCG
- Популярное решение без separability
-
Тяжело перейти с GSP
-
Yahoo: 20% ожидаемое падение выручки
-
Google Adwords
Allocation curves
Обобщения GSP?
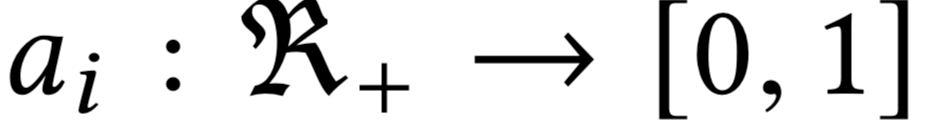
фиксируем \(b_{-i}\)
Allocation curves: преимущества
- Гибкость:
- подходит для разных механизмов цен
- можно вычислить GSP-пороги
- можно вычислить VCG-цены
- Прозрачность:
- прогнозы и проверки
- информация для биддеров
- анализ цен
Allocation curves: separability
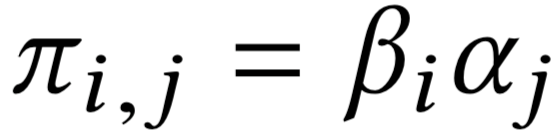
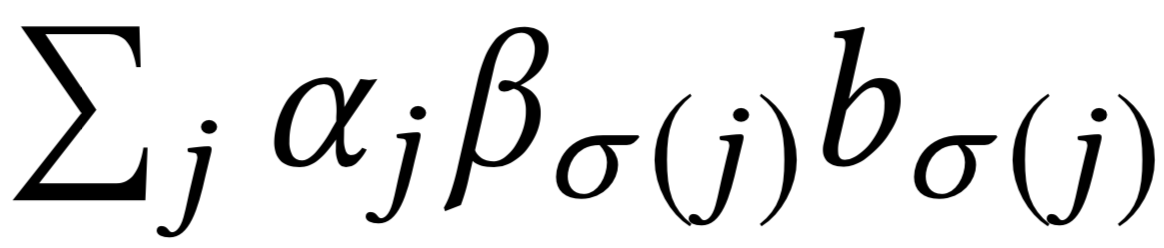
\(\sum_j \pi_{\sigma(j), j} b_{\sigma(j)} \;=\)
\(\max \; SW \)
Allocation curves: separability

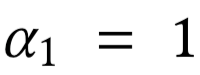
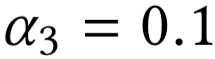
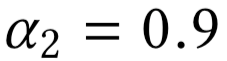

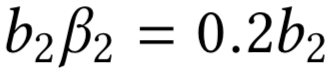

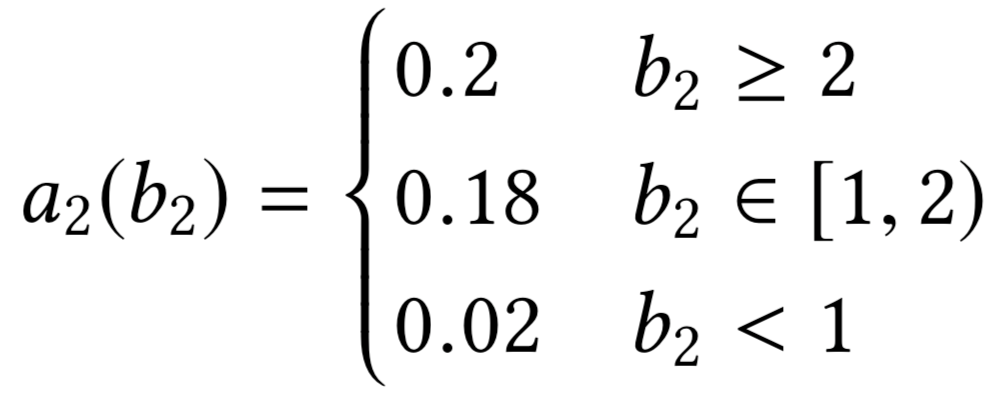
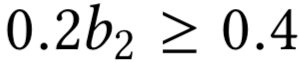
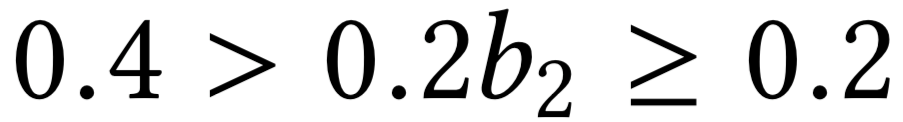
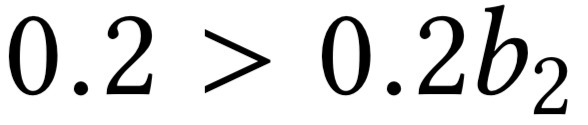
Allocation curves: non-separability
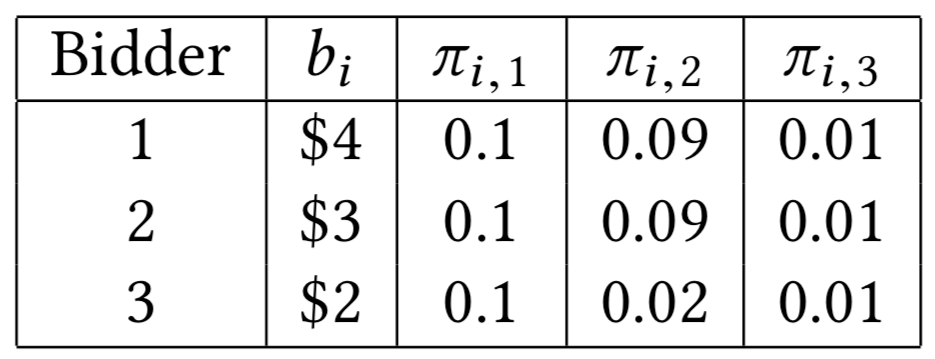
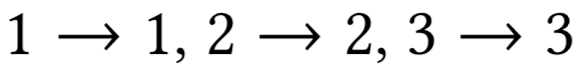
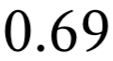
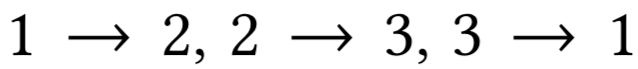
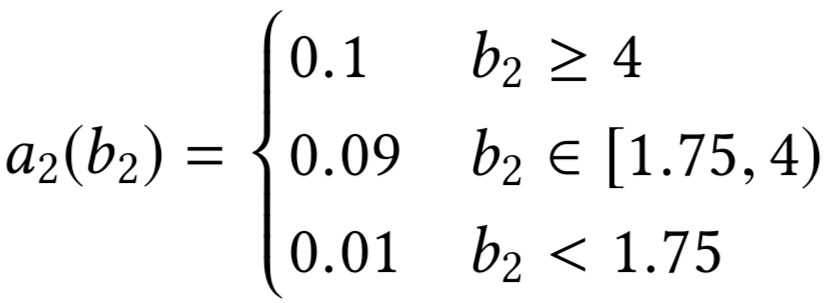
Наивный алгоритм
Пусть ставки сделаны с точностью до цента
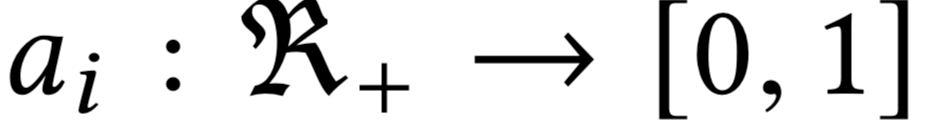
Для фиксированного \(i \in I\) найдём
- Для каждого слота \(j \in J\)
- Бинпоиск ставки за \(O(\log(100b_i))\)
- Поиск max паросочетания за \(O(nm^2)\)
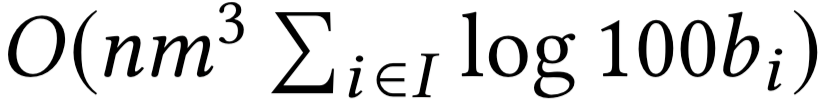
Мы найдём все \(a_i(.)\) за \(O(nm^2)\) !
Multi-dimensional bidding
Думаем про конверсии:
-
Покупка
-
Загрузка приложения
-
Создание аккаунта
-
Чтение сайта долгое время

Multi-dimensional bidding

Multi-dimensional bidding
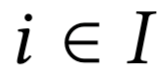
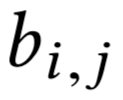
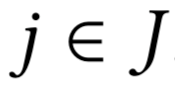
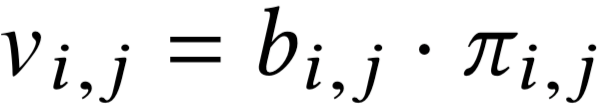

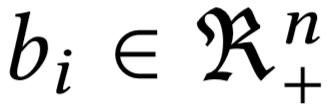
ожидаемая польза:
Мы снова найдём все \(f_i(.)\) за \(O(nm^2)\) !
Структура \(a_i(.)\)
Утверждение
\(a_i(b) = p_i\) возрастает с увеличением \(b\)
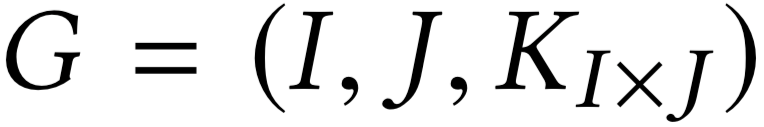
пусть не так:
Часть 2,
алгоритмическая
slabod@
MEM-seminar, 09.04.2019
Напоминание
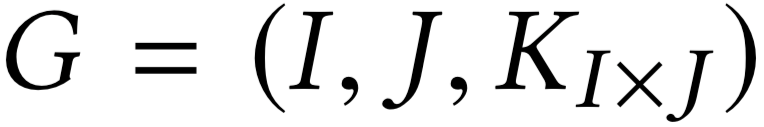
\(\sigma(.):\) \(V^{\sigma} \,= \, \sum_j \pi_{\sigma(j), j} b_{\sigma(j)} \; \to \max\)
\(\sigma: J' \to I \)
\(\sigma(j) = i \)
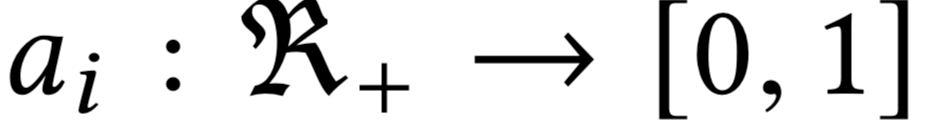
Напоминание
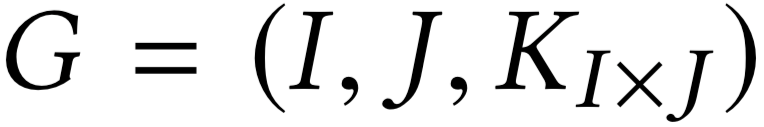
\(\sigma^* = \argmax(V^{\sigma})\)
\(\sigma^*(j) = j \)
\(\sigma^*\)
План
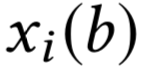

- Венгерский метод для максимального паросочетания
- Max паросочетание с \(\sigma(j) = i\)
— min путь в \(G\) между вершинами \(i, j\) - Floyd–Warshall \(\Rightarrow\) все пути \(\Rightarrow\) allocation curves
- Алгоритм 1 за \(O(n^3)\)
- Алгоритм 2 за \(O(nm^2)\)
Граф возможностей (augmentation graph)

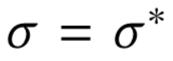
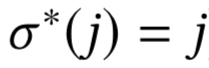
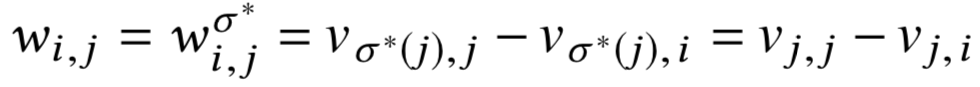

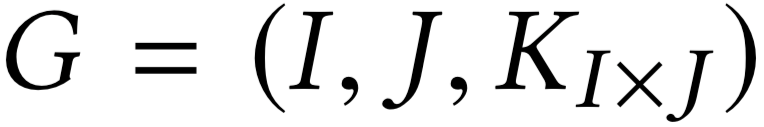

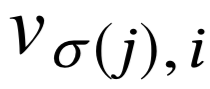
Граф изменений (augmentating subgraph)
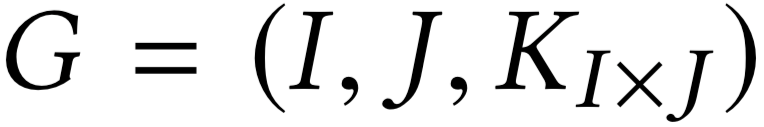
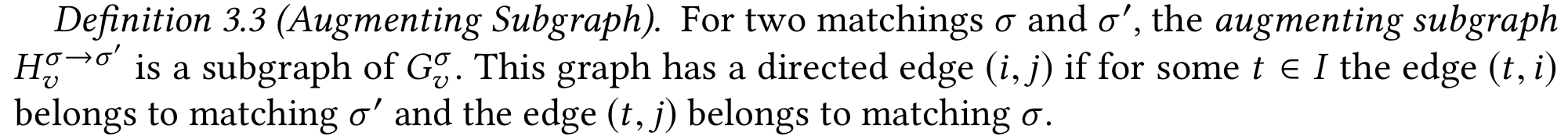
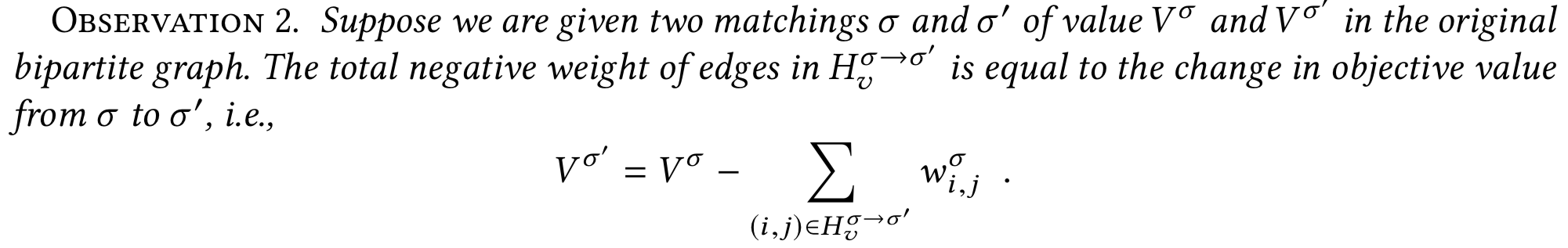
\(t\) единственно
Свойства \(H^{\sigma \to \sigma'}\): структура
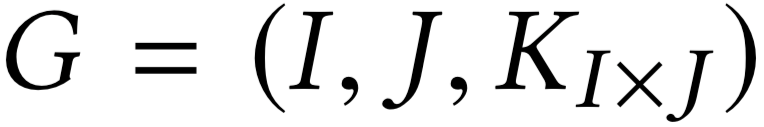

все входящие и исходящие степени
в \(H^{\sigma \to \sigma'}\) равны \(1\)
Свойства \(H^{\sigma \to \sigma'}\): циклы
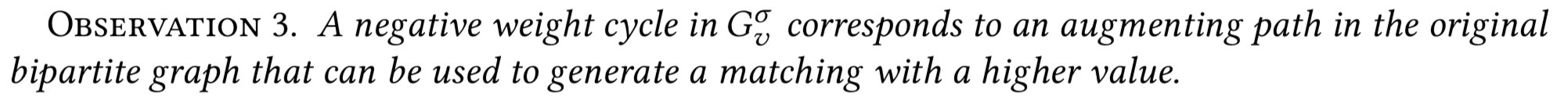
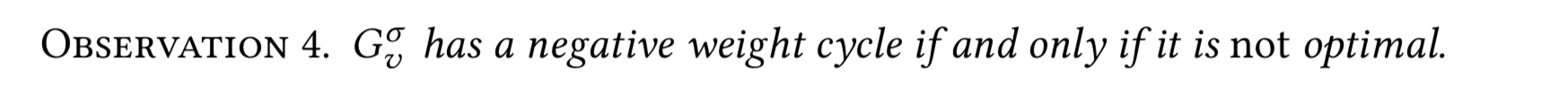
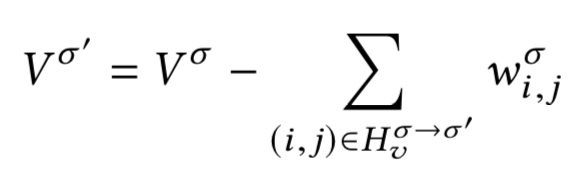
очевидно
\(H\) разбивается на циклы
Фиксирование \(\sigma(x) = y\)

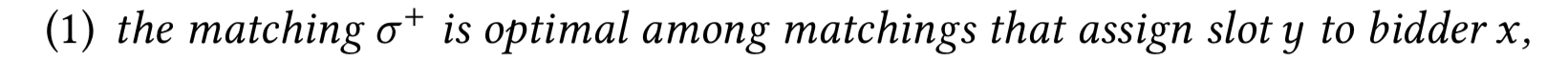

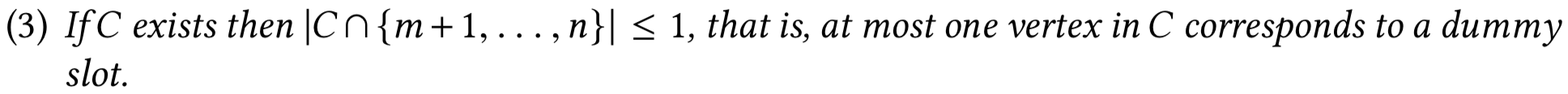
Фиксирование \(\sigma(x) = y\)



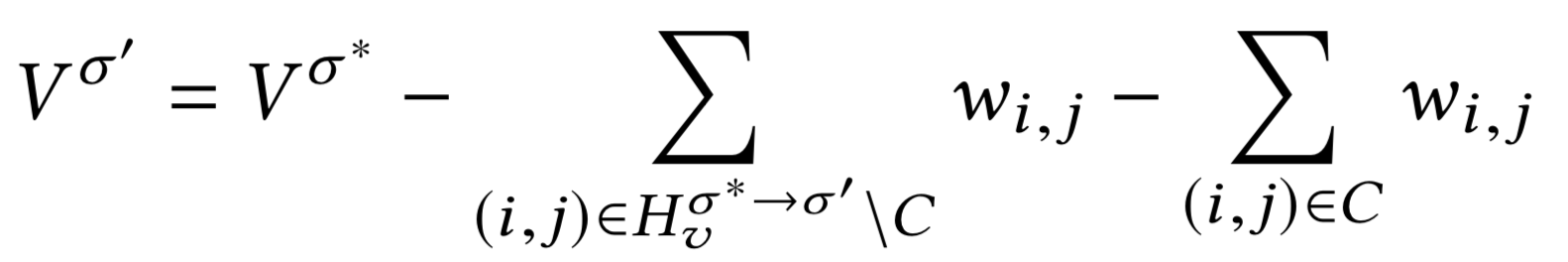
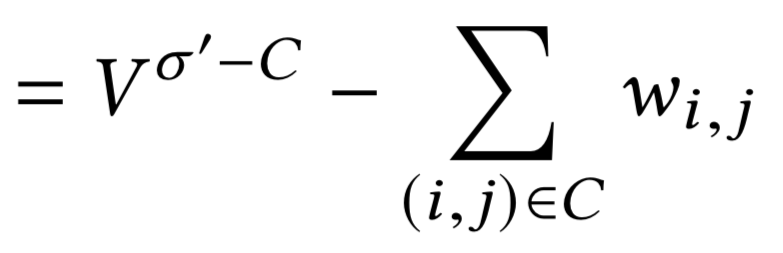


Фиксирование \(\sigma(x) = y\)

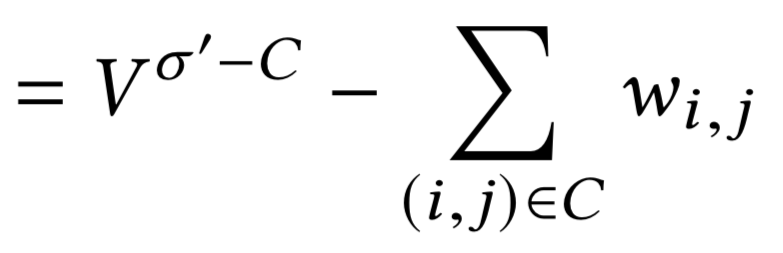

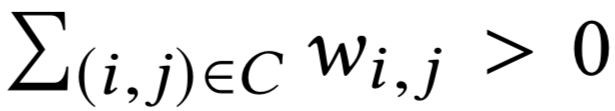
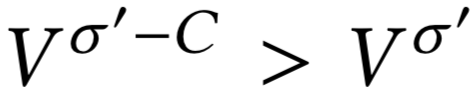
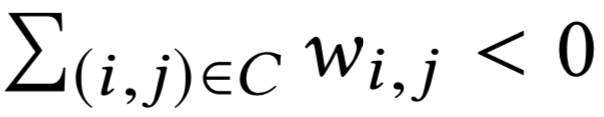

\(\sigma'\) не оптимально
отрицательный цикл в \(G_v\)
\(\sigma^*\) не оптимально
Фиксирование \(\sigma(x) = y\)
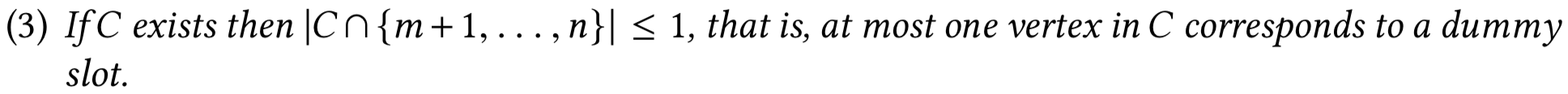
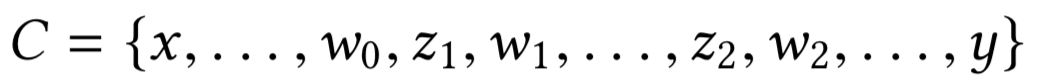
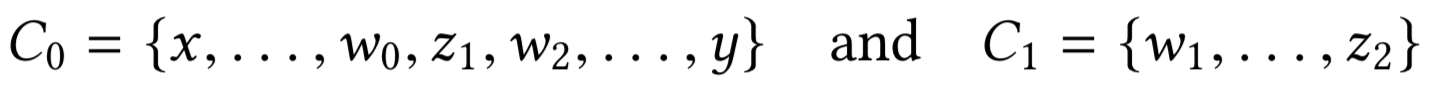

Кратчайшие пути


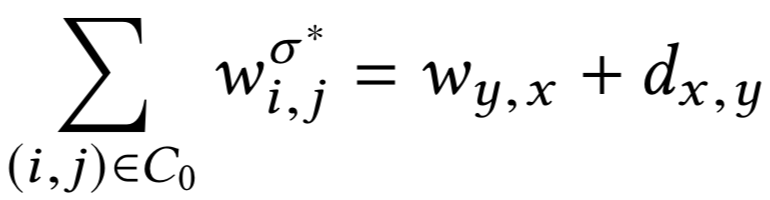
Обратная \(\sigma\)
\(\sigma: J' \to I \)
\(\sigma(j) = i \)
\(\sigma^{-1}: I \to J' \)
\(\sigma^{-1}(i) = j \)
\(V^{\sigma}_{-i} \,= \, V^{\sigma} - \pi_{i, \sigma^{-1}(i)} b_i\)
\(\pi_{\sigma(j), j} b_{\sigma(j)} \,=\, \pi_{i, \sigma^{-1}(i)} b_i\)
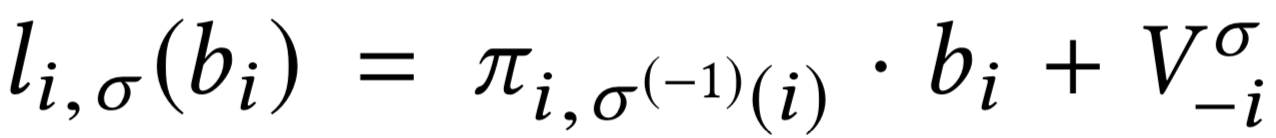
\(V^{\sigma} \,= \, V^{\sigma}_{-i} + \pi_{i, \sigma^{-1}(i)} b_i\)
для произвольной ставки \(b_i:\)
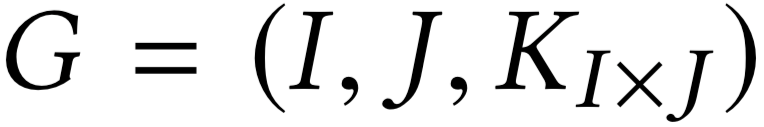
Configuration line
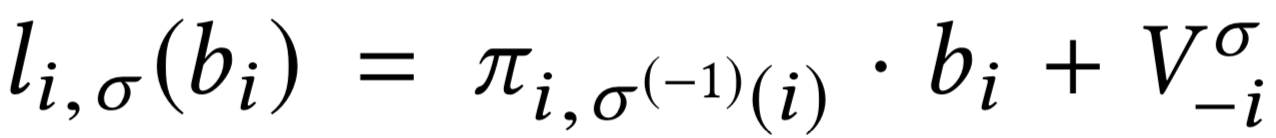
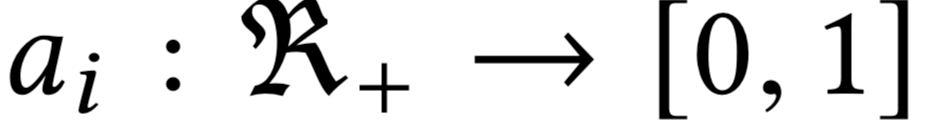
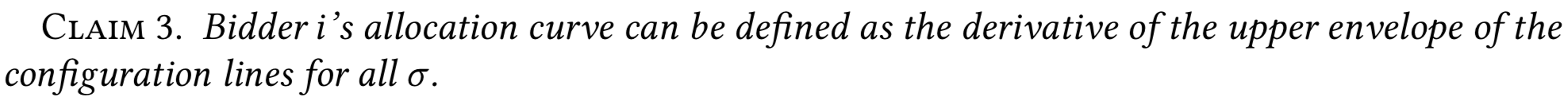
(здесь докладчик рисует картинки
и машет руками)
Нужные configuration line
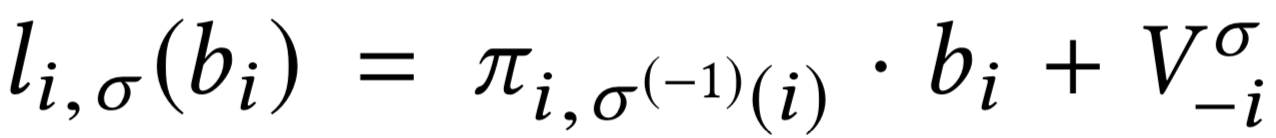


коэффициент \(\pi_{x, y}\) постоянен
максимизируем \(V^{\sigma}_{-x}\) по \(\sigma\)

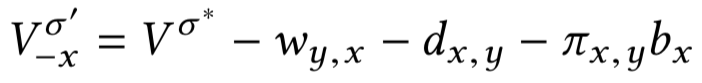
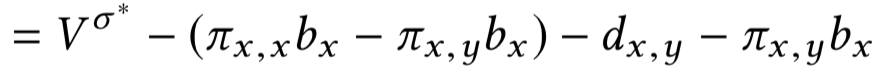
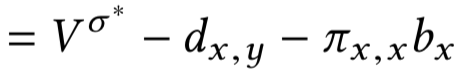


Upper envelope для \(m\) прямых за \(O(m^2)\)
- Пусть даны \(m\) прямых вида \(y = a_i x + b_i\)
- Добавляем прямые по очереди
- Для каждой сохраняем её отрезки максимальности
-
При добавлени:
- ищем \(\le m\) точек пересечения,
- \(\le 2\) из них максимальны
- Изменяем \(\le m\) отрезков максимальности
Спасибо за внимание!
