Shenfun - automating the spectral Galerkin method

Associate Professor Mikael Mortensen

Department of Mathematics

Division of Mechanics

University of Oslo

 

MekIT'17, Trondheim 11/5 - 2017

Spectral methods

what? why?  where?

  • Global basis (test) functions
  • Typically Chebyshev or Legendre polynomials or Fourier exponentials
  • Simple tensor product grids
  • Smooth solutions
u(x) = \displaystyle\sum_{k=0}^{N-1} \hat{u}_k \phi_k(x)

Solution

Expansion coefficients

(unknowns)

Test functions

Spectral methods

what? why? where?

  • Accuracy!
  • Efficiency! Fast Fourier transforms
  • and they're cool
u(x) = \displaystyle\sum_{k=0}^{N-1} \hat{u}_k \phi_k(x)

Solution

Expansion coefficients

(unknowns)

Test functions

Why not? Only simple cartesian domains unless you do spectral elements

Spectral methods

what? why? where?

3D + time and HUGE resolution

Serious number crunching - extreme computing

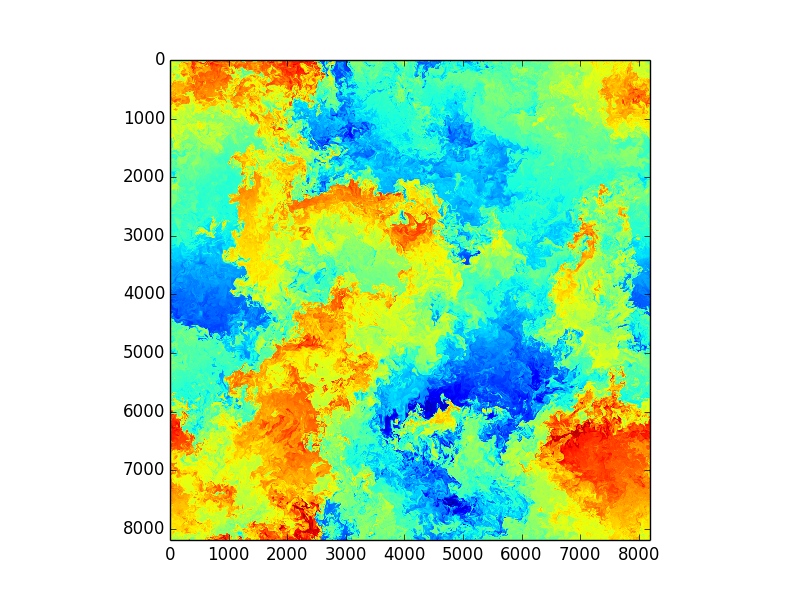
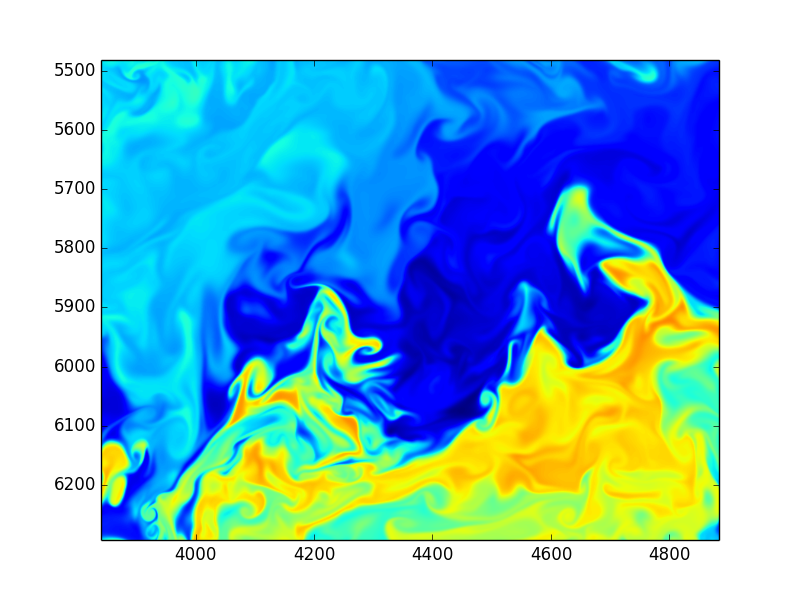
Images from huge spectral DNS simulations by S. de Bruyn Kops, UmassAmherst, College of Engineering

  • Direct Numerical Simulations (DNS)
  • Turbulent/transitional flows
  • Instabilities/perturbations
  • +++

DNS codes are usually written using low-level Fortran or C. Does it have to be this way?

Isn't it possible to do this just as well in a nice language like Python?

What does it really take to build a spectral DNS solver?

Numpy is designed around structured arrays that can be reshaped, resized, sliced, transposed, etc. 

Most array operations are performed in C and are very fast

  (1)  Structured grid

  (2)  3D parallel FFT

Numpy wraps FFTpack

pyFFTW wraps FFTW

No MPI

But mpi4py wraps almost  the entire MPI library and is as efficient as low-level C

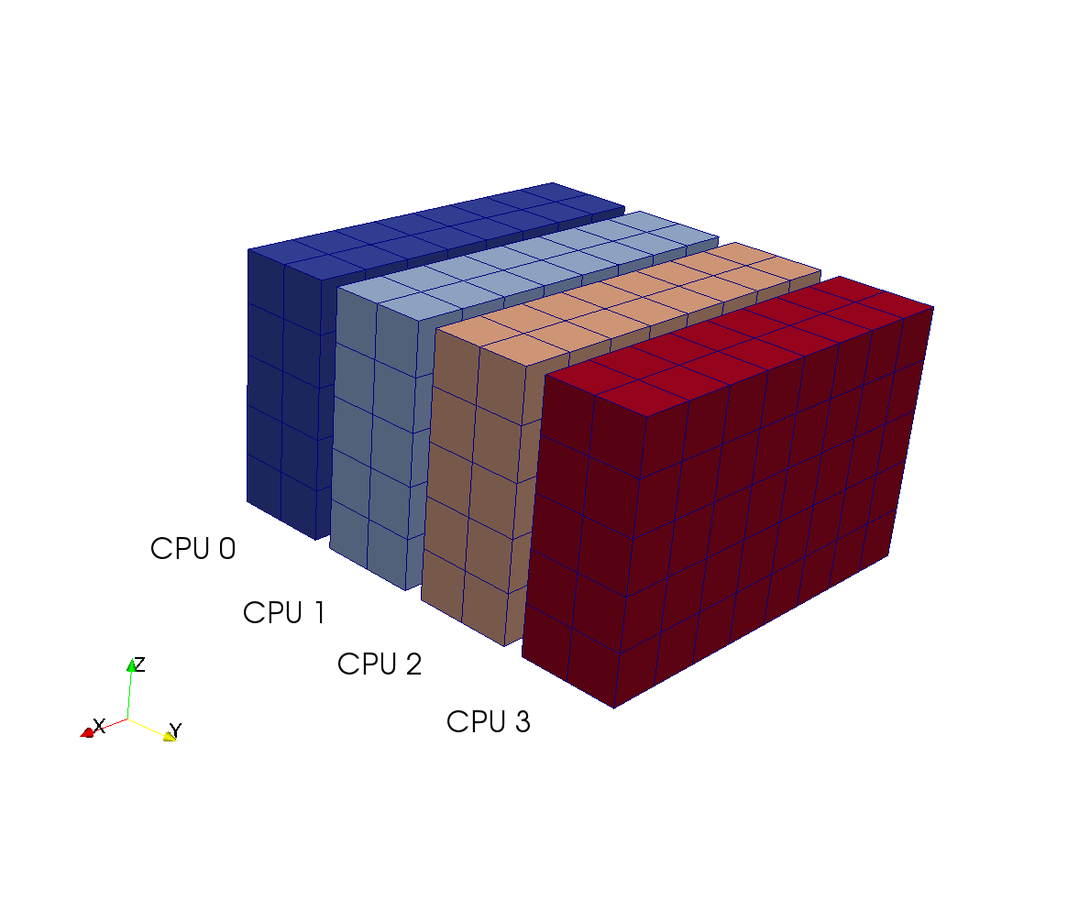
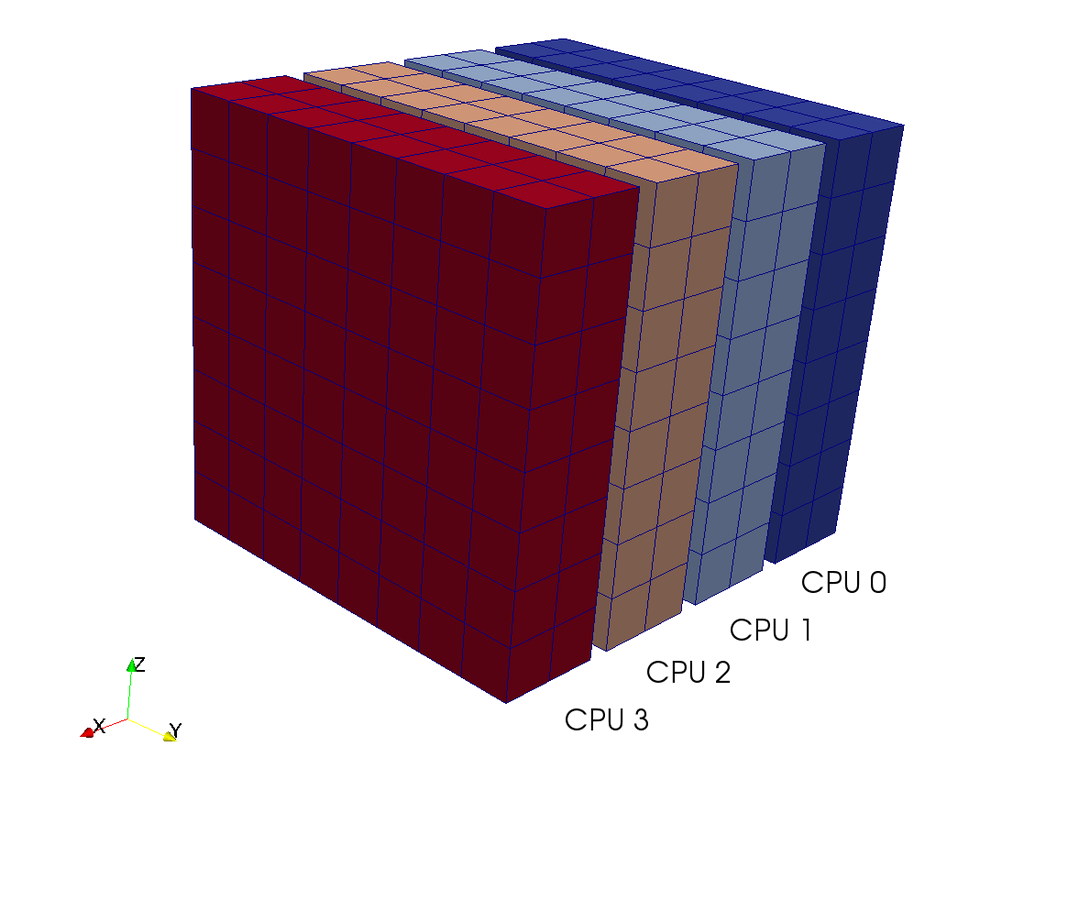
3D FFT with MPI

Slab decomposition (max N CPUs)

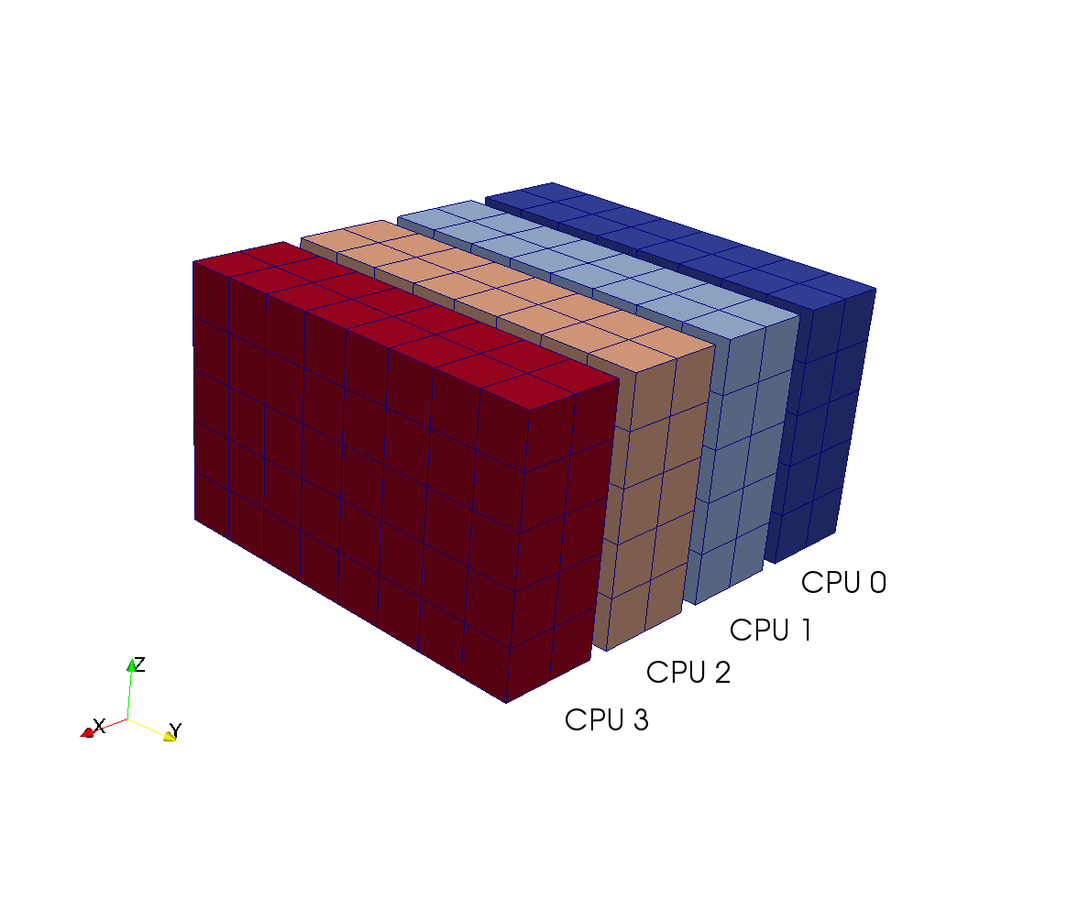
rfft2(a, axes=(0,1))

fft(a, axis=2)

Real space

Spectral space

4 processors - 4 colours

Do serial FFTs on local data

then transfer and realign datastructures

Do FFT in newly aligned direction

 

MPI.Alltoall

With now publicly available packages in

mpiFFT4py

https://github.com/spectralDNS/mpiFFT4py

mpi4py-fft

https://bitbucket.org/mpi4py/mpi4py-fft

With Licandro Dalcin at KAUST

Completely generic implementation - 500 lines of  Python code

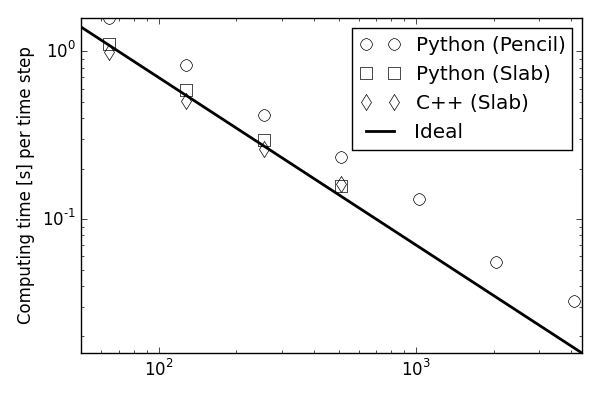
Both scaling very well on

thousands of CPUs

With parallel 3D FFT we may develop DNS solvers 

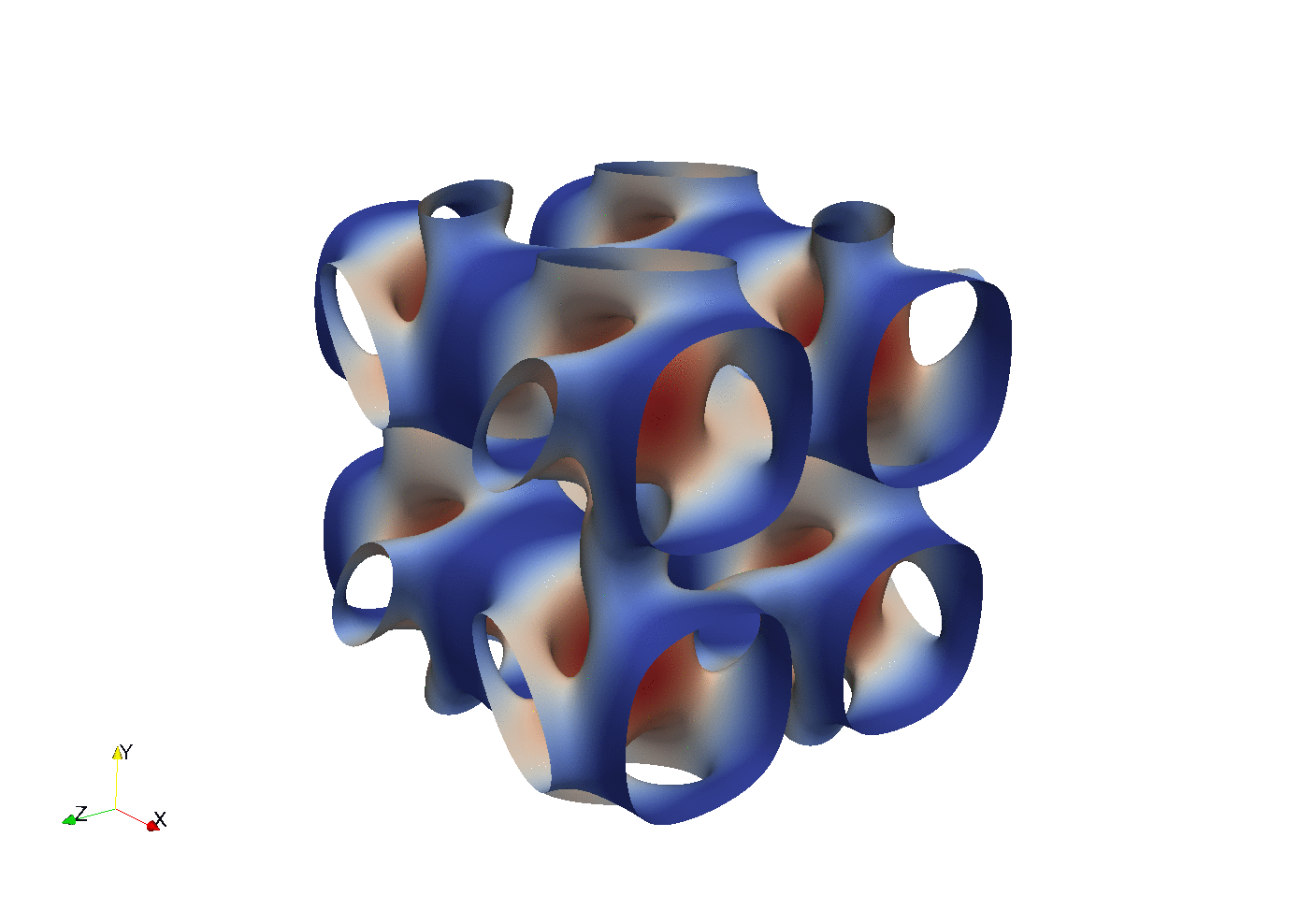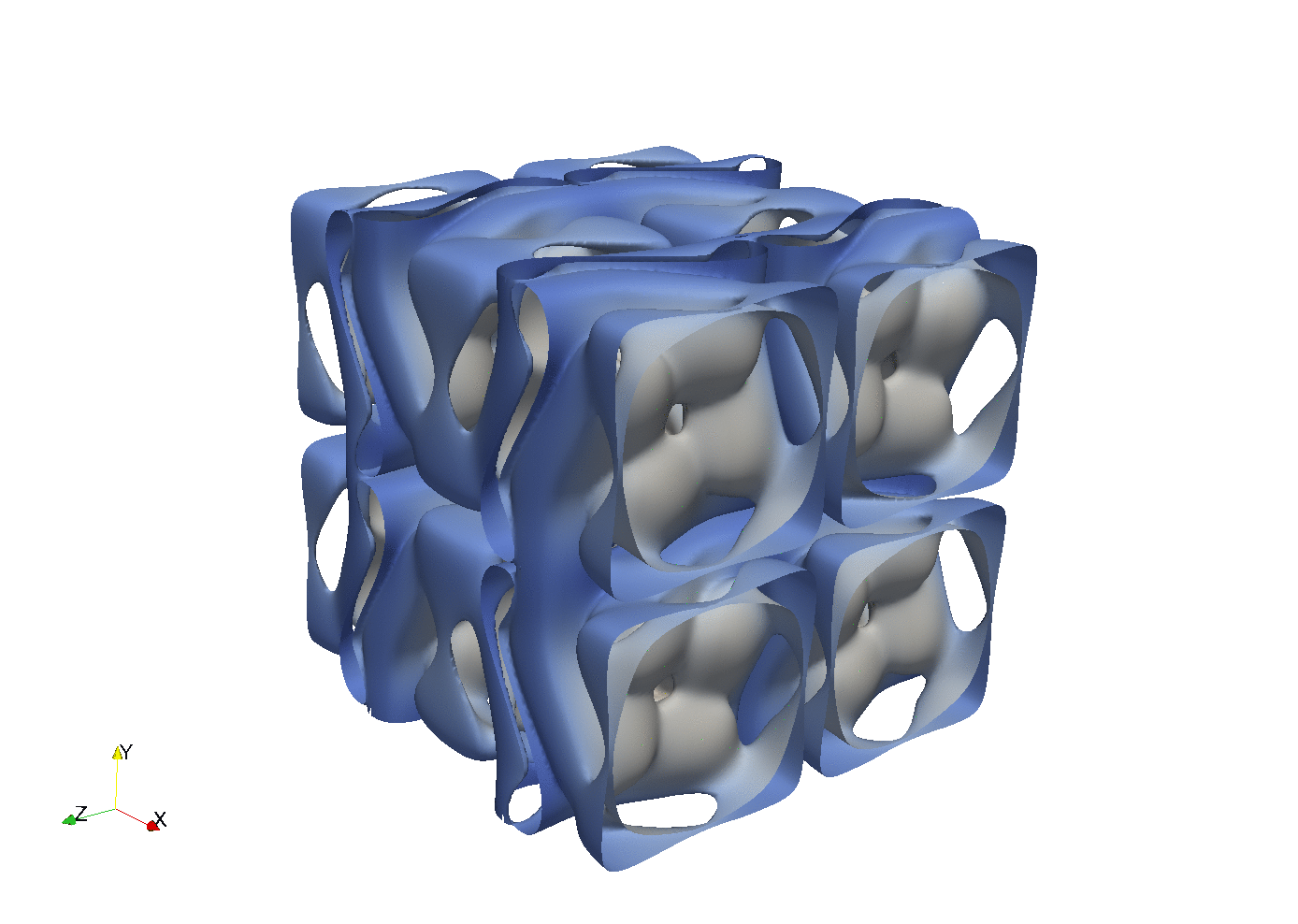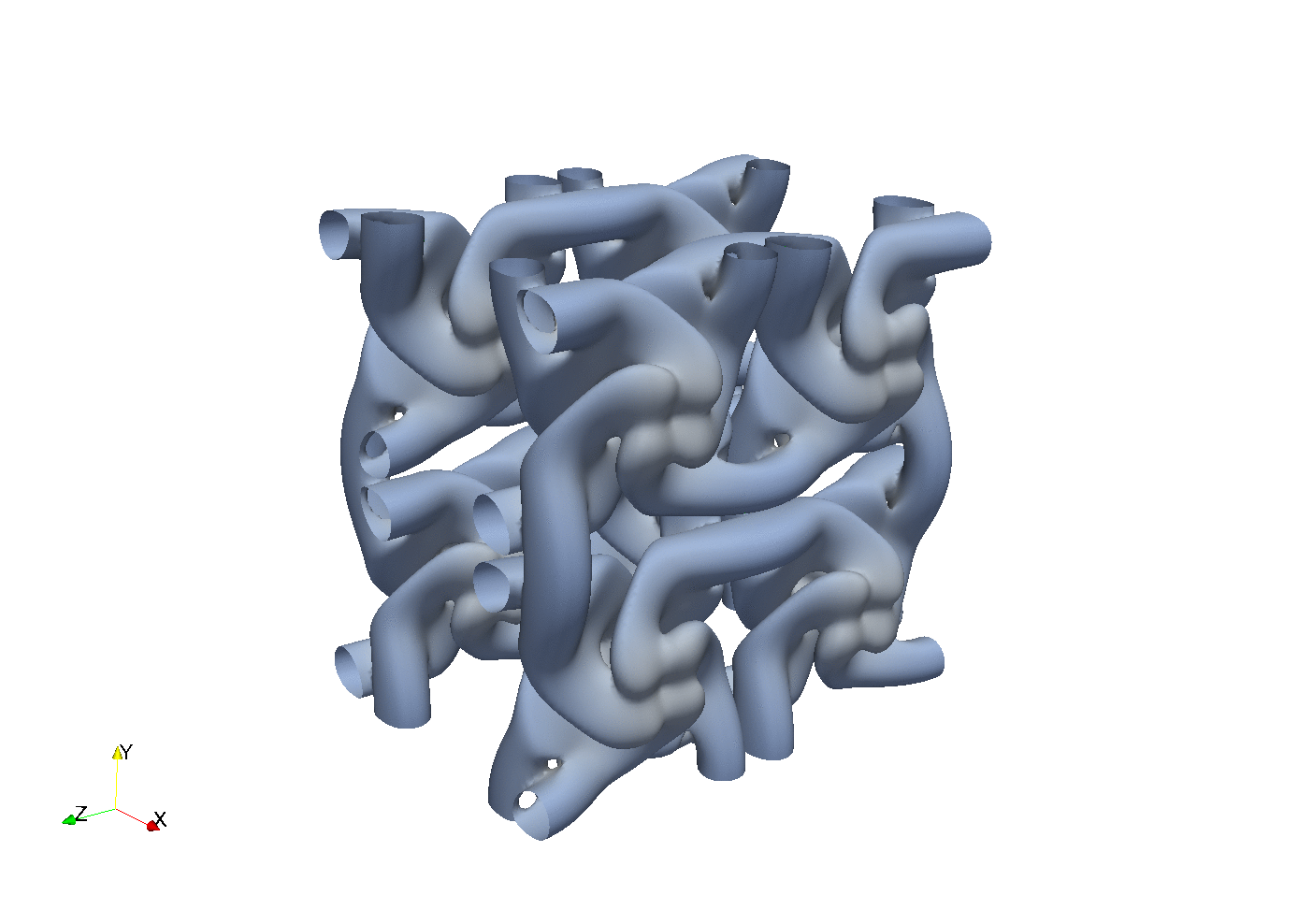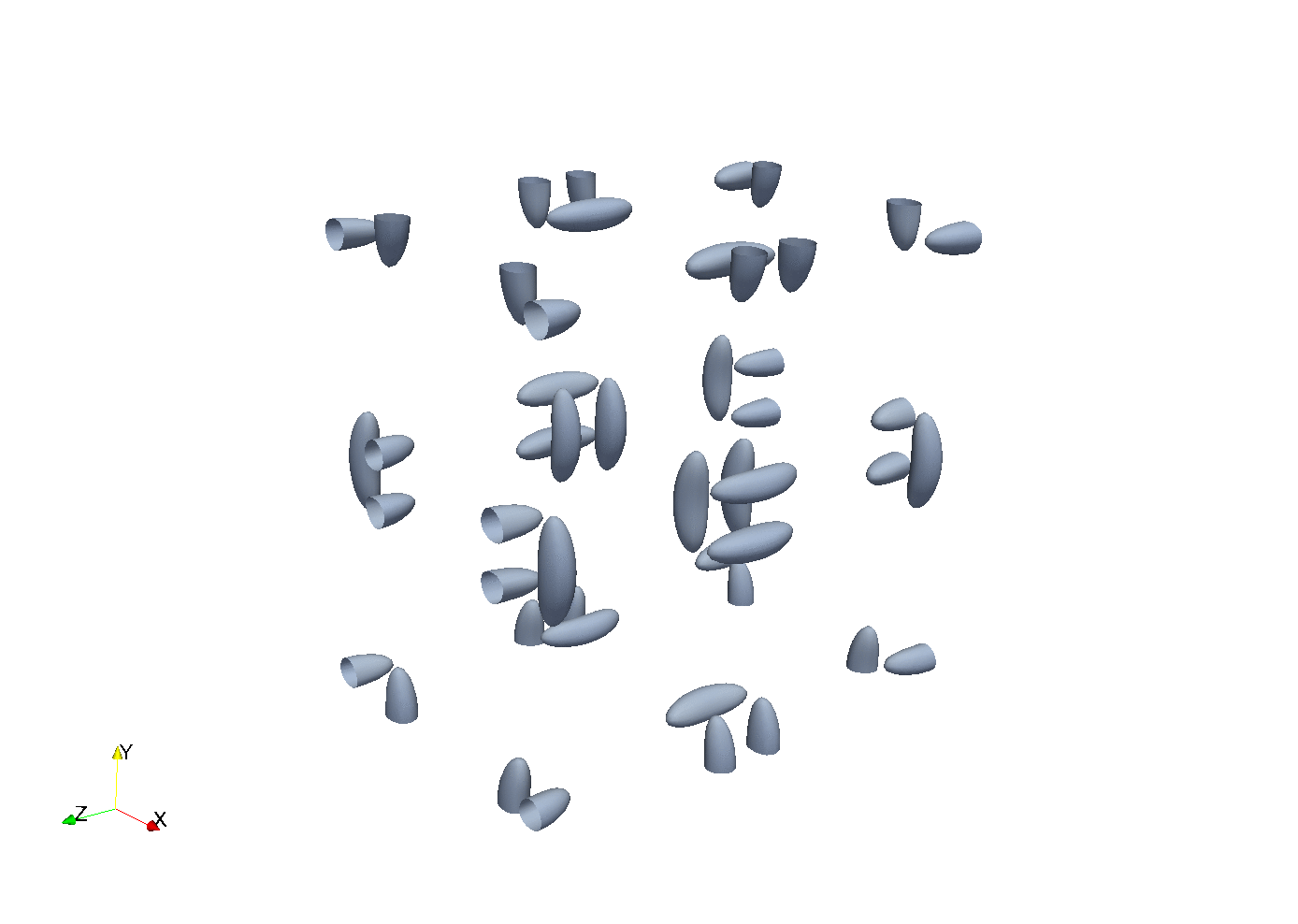
Enstrophy colored by pressure

which turns out to be very easy, and

100 lines of compact Python code is enough to implement

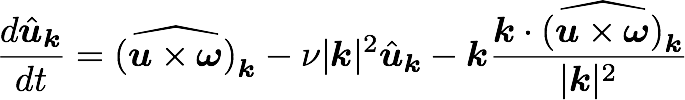
Approximately 30% slower than C

Easily optimized the last 30% using Cython

Using just Fourier

Navier-Stokes is easy, what about other PDEs? non-periodic BCs?

\phi_k(x) = T_k(x)-T_{k+2}(x)
\phi_k(x) = L_k(x) - L_{k+2}(x)

Chebyshev

Legendre

(1) Choose spectral basis functions satisfying boundary conditions, e.g.:

\phi_k(\pm 1) = 0

(2) Transform PDEs using the method of weighted residuals -> variational forms

Best answer: The Spectral Galerkin method

Sounds easy? - Let's automate!

shenfun

from fenics import *

mesh = UnitSquareMesh(8, 8)
V = FunctionSpace(mesh, 'CG', 1)

# Define variational problem
u = TrialFunction(V)
v = TestFunction(V)
f = Constant(-6.0)
a = inner(grad(u), grad(v))*dx
L = f*v*dx

Solve equations with code very similar to mathematics

However

  • Finite accuracy (not spectral)
  • Not optimal for simple tensor product grids or DNS

How to automate?

What do we know about

automating the solution

of PDE'S?

Shenfun

Python package for automating the spectral Galerkin method

for high performance computing on tensor product grids

A FEniCS like interface with a simple form language

Extremely fast solvers for Poisson, Helmholtz and Biharmonic problems

MPI - invisible to the user

Fourier - Chebyshev - Legendre

modified basis functions

What else is there?

Chebfun

Spectral collocation, MATLAB, structured, no MPI

Semtex 

Spectral element, MPI, C++/Fortran, 2D unstructured (1 Fourier)

Quite low-level, nowhere near as easily configured as FEniCS for new types of equations.

Very good for Navier-Stokes

Nek5000

Spectral element, Fortran, MPI, 3D unstructured

Nektar++

Spectral hp-element, C++, 3D unstructured

Nothing really for fast development of new spectral solvers aimed at high performance computing on supercomputers

Spectral Galerkin

Poisson example

\nabla^2 u(x) = f(x) \quad \text{for} \quad x \in [-1, 1]
u(\pm 1) = 0

Create a basis that satisfies boundary conditions, e.g.,

\phi_k(x) = T_k(x) - T_{k+2}(x) \quad V = \text{span}\{\phi_k\}_{k=0}^{N-3}
\displaystyle \int_{-1}^{1}v \nabla^2 u \, w dx = \int_{-1}^{1} vf w dx \quad \text{for all} \, v \in V
\text{Find } u \in V, \text{such that}
\text{where } w(x) \text{ is a weight function and } v \text{ is a test function}

Shenfun implementation

import numpy as np
from shenfun import TestFunction, TrialFunction, inner, div, grad, chebyshev

N = 20
V = chebyshev.ShenDirichletBasis(N, plan=True)
v = TestFunction(V)
u = TrialFunction(V)

# Assemble stiffness matrix
A = inner(v, div(grad(u)))

# Some consistent right hand side
f = Function(V, False)
f[:] = -2

# Assemble right hand side
f_hat = inner(v, f)

# Solve equations and transform spectral solution to real space
f_hat = A.solve(f_hat)
fj = V.backward(f_hat)

x = V.mesh(N)
assert np.allclose(fj, 1-x**2)

Very similar to FEniCS!

just with spectral accuracy

(1) Create basis

(2) Variational forms

2D/3D Tensor product spaces

Combinations of Fourier and Chebyshev/Legendre bases

u(x,y,z,t) = \displaystyle \sum_{k}\sum_{l}\sum_{m} \hat{u}_{k,l,m}(t) \phi_k(x)\phi_l(y)\phi_m(z)
W(x,y,z) = V(x) \times V(y) \times V(z)

Any combination of spaces (ultimately)

With solutions of the form:

Unknown expansion coefficients

2D/3D Tensor product spaces

Combinations of Fourier and Chebyshev/Legendre bases

from shenfun import *
from mpi4py import MPI

comm = MPI.COMM_WORLD
N = (20, 30)
V0 = chebyshev.ShenDirichletBasis(N[0])
V1 = fourier.R2CBasis(N[1])
T = TensorProductSpace(comm, (V0, V1))
v = TestFunction(T)
u = TrialFunction(T)

A = inner(v, div(grad(u)))

# Or 3D
V2 = fourier.C2CBasis(40)
T3 = TensorProductSpace(comm, (V0, V2, V1))
v = TestFunction(T3)
u = TrialFunction(T3)

A = inner(v, div(grad(u)))

MPI under the hood

using mpi4py-fft

on tensor product grids like:

A simple form language

to make implementation very similar to mathematics

Mathamatical operators act on test, trial, or functions with data 

V = TensorProductSpace(comm, (V0, V1, V2))

# Form arguments:
v = TestFunction(V)
u = TrialFunction(V)
u_ = Function(V, False)

# Forms
du = grad(u_)
d2u = div(du) 
cu = curl(du)
dudx = Dx(u_, 0)

Inner products and projections

A = inner(v, u)    # Bilinear form, assembles to matrices
f = inner(v, u_)   # Linear form, assembles to vector
project(div(grad(u_)), V)  # projection to V

Fast transforms

(not in FEniCS)

u_ = V.backward(u_hat, u_)

Any spectral function is defined as

u(x) = \displaystyle\sum_{k=0}^{N-1} \hat{u}_k \phi_k(x)
u(x,y,z) = \displaystyle\sum_{k=0}^{N-1} \sum_{l=0}^{N-1} \sum_{m=0}^{N-1} \hat{u}_{klm} \phi_k(x)\phi_l(y)\phi_m(z)

3D:

1D:

This is computed on the tensor product grid as a backwards transform,

e.g., a discrete Fast Fourier inverse transform

A non-periodic basis uses fast Chebyshev transforms

Fast forward transforms

by L2-projections

u_hat = V.forward(u_, u_hat)
(u_h, v_h) = (Iu, v_h)\quad \forall \, v_h \in V_h
\text{Find } u_h \in V_h, \text{such that}

which is achieved using a forward transform

Implemented with FFTs or fast Chebyshev transforms

Vector spaces

VectorTensorProductSpace

import numpy as np
from shenfun import *

N = 16
K0 = C2CBasis(N)
K1 = C2CBasis(N)
K2 = R2CBasis(N)
T = TensorProductSpace(comm, (K0, K1, K2))

# Scalar function u_
u_ = Function(T, False)
u_hat = Function(T)
u_[:] = np.random.random(u_.shape)
u_hat = T.forward(u_, u_hat)

# Now define vector space to allow computation of grad(u_)
TV = VectorTensorProductSpace([T]*3)
du_hat = project(grad(u_), TV, uh_hat=u_hat)

Nonlinearities

are all treated with pseudospectral techniques

\nabla u \times \nabla \times u
u \cdot u
u | u |^2

(1) Compute inverse

u = T.backward(u_hat)

with dealiasing using

3/2-rule (padding) or 2/3-rule

(3) Transform back to spectral space

w = u*u

(2) Compute nonlinearity

w_hat = T.forward(w)
T = TensorProductSpace(comm, (V0, V1, V2))

Complex Ginzburg-Landau

example

\frac{\partial u}{\partial t} = \nabla^2 u + u -(1+1.5i)u |u|^2


2D periodic (x, y) \( \in [-50, 50]^2 \)

Use Fourier in both directions

Weak form, only spatial discretization

\frac{\partial (v, u)^N}{\partial t} = -(\nabla v, \nabla u)^N + (v, u -(1+1.5i)u |u|^2)^N
(2\pi)^2\frac{\partial \hat{u}}{\partial t} = -(\nabla v, \nabla u)^N + (v, u -(1+1.5i)u |u|^2)^N

Complex Ginzburg-Landau

example

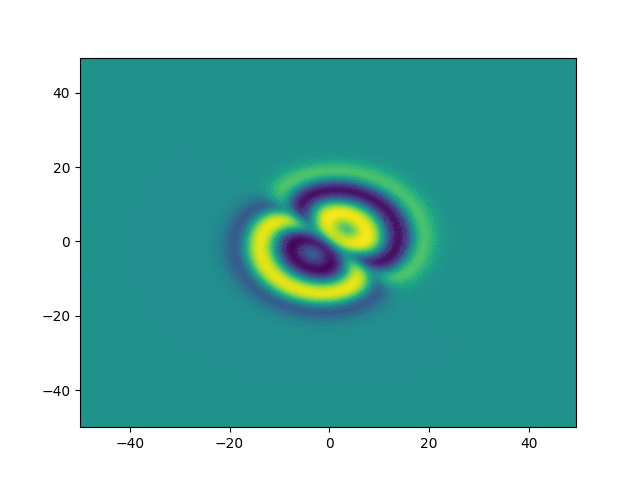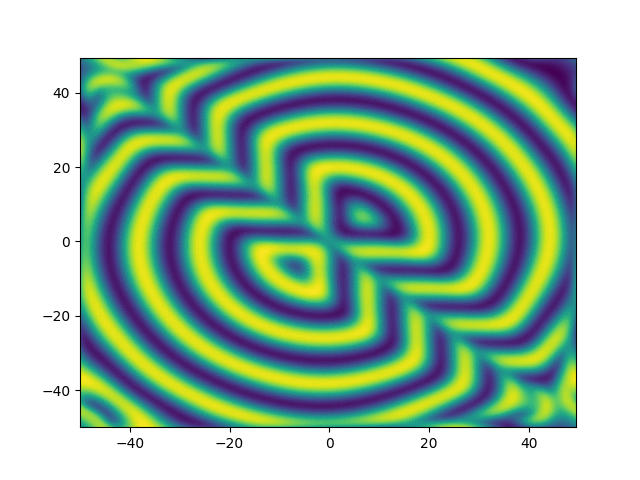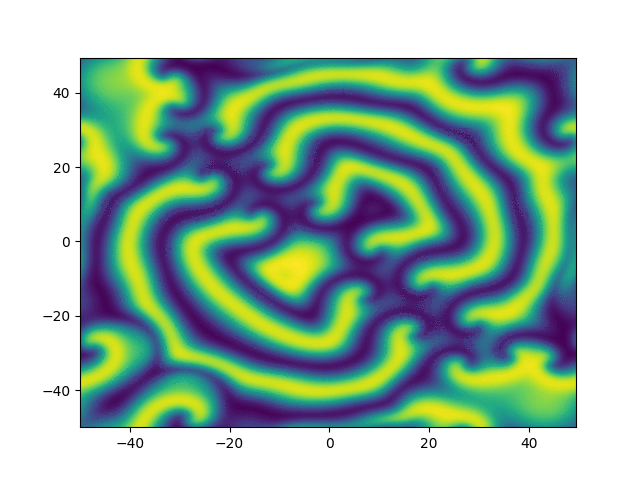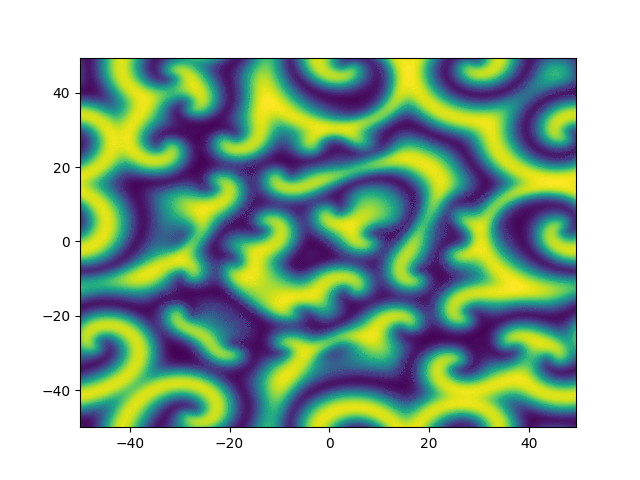
\frac{\partial u}{\partial t} = \nabla^2 u + u -(1+1.5i)u |u|^2


2D periodic (x, y) \( \in [-50, 50]^2 \)

import sympy
from shenfun.fourier.bases import R2CBasis, C2CBasis
from shenfun import inner, grad, TestFunction, TrialFunction, Function, \
    TensorProductSpace

# Use sympy to set up initial condition
x, y = sympy.symbols("x,y")
ue = (x + y)*sympy.exp(-0.03*(x**2+y**2))

N = (200, 200)
K0 = C2CBasis(N[0], domain=(-50., 50.))
K1 = C2CBasis(N[1], domain=(-50., 50.))
T = TensorProductSpace(comm, (K0, K1))
u = TrialFunction(T)
v = TestFunction(T)

def compute_rhs(rhs, u_hat, U, Up, T, Tp, w0):
    rhs.fill(0)
    rhs = inner(grad(v), -grad(U), output_array=rhs, uh_hat=u_hat)
    rhs /= (2*np.pi)**2
    rhs += u_hat
    rhs -= T.forward((1+1.5j)*U*abs(U)**2, w0)
    return rhs

# And, e.g., Runge-Kutta integrator
#
#

Key code:

Navier Stokes 

Turbulent channel flow

3D tensor product space

2 Fourier bases +

Modified Chebyshev bases for wall normal direction

Kim and Moin modified version of Navier-Stokes:

\mathcal{H}

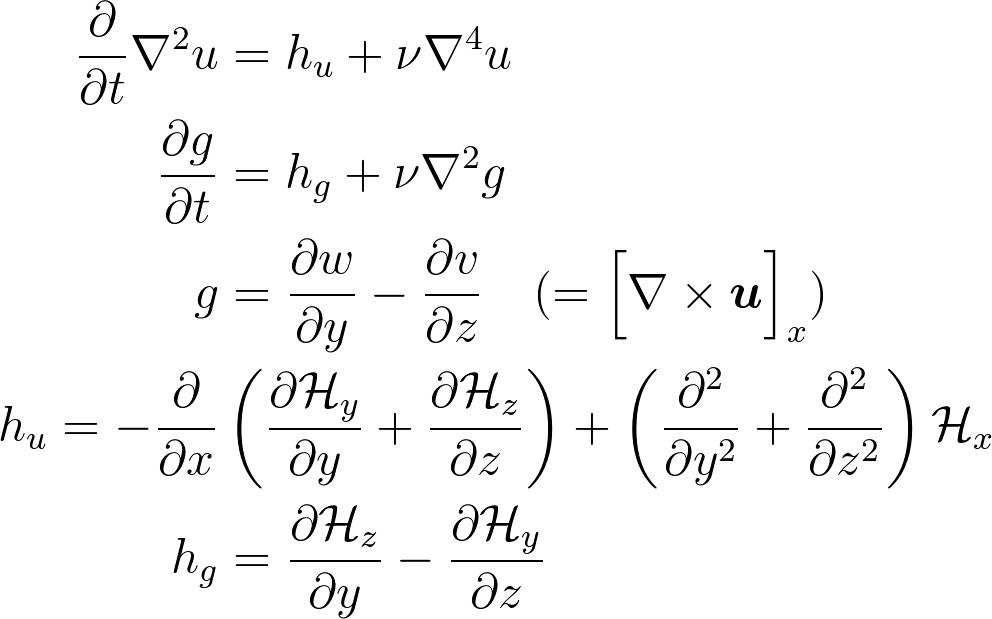
is convection

Wall normal velocity

Wall normal vorticity

Navier Stokes 

Turbulent channel flow

512\times 1024\times 1024

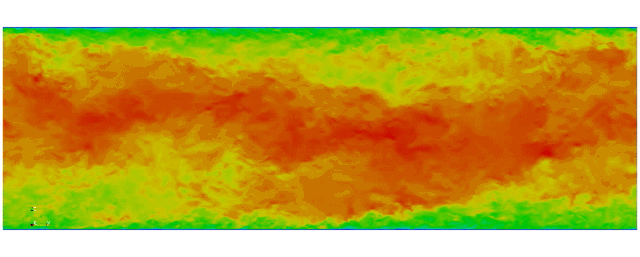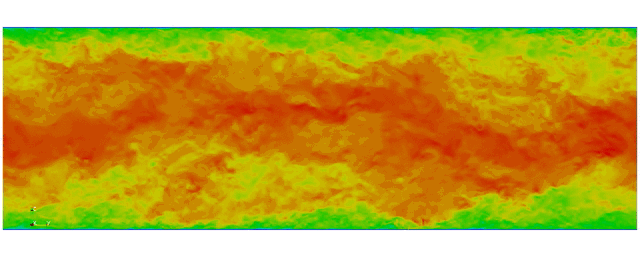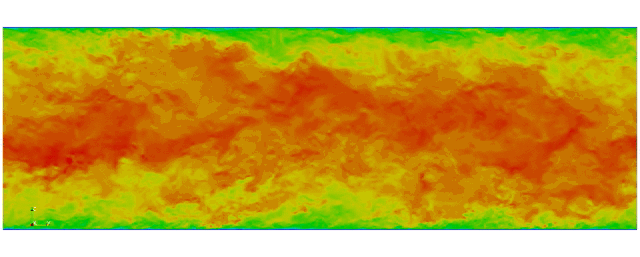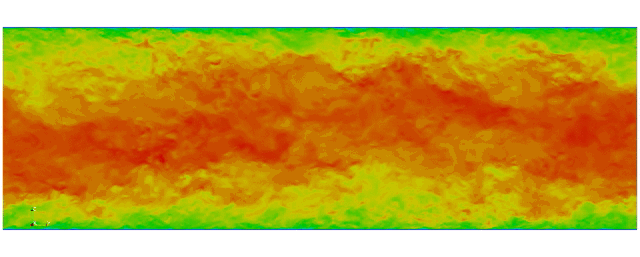
1 sec per time step on 512 cores

Tensor product mesh:

Shaheen II at KAUST

Thank you for your time! Questions?

http://github.com/spectralDNS

Made with Slides.com