The SpectralDNS project:

Shenfun - automating the spectral Galerkin method

Associate Professor Mikael Mortensen

Department of Mathematics, Division of Mechanics, University of Oslo

I3MS-seminar RWTH Aachen University 6/11 - 2017

Outline of talk

Python for high performance scientific computing

Shenfun

A software for automating the spectral Galerkin method

Github pushes by language (2017):

  • An extremely usable, high-level programming language
  • Very popular in the scientific computing community
  • Open source
  • Interpreted "scripting" language (no compilation)

Python vs Matlab

Python is often compared to Matlab, because a lot of the coding done in either is similar

  1. Python is a programming language, whereas Matlab is a numerical computing environment. Numpy+Scipy+Matplotlib is a numerical computing environment in Python.
  2. Python is open source and free, whereas Matlab is very expensive.
  3. Both have strong support for array manipulations and  vectorization/slicing of arrays.
  4. Both are interpreted scripting languages. No compilation
  5. Python is easy to extend with MPI - Matlab is not
Matlab Python/Numpy Operation
find(a>0.5) nonzero(a>0.5) find the indices where (a > 0.5)
zeros((3,4,5)) zeros(3,4,5) Create array of shape (3,4,5)
eye(3) eye(3) 3x3 identity matrix

Some similarities and differences:

Anaconda Python

If you want to get started with scientific computing in Python

Comes pre-loaded with (almost) everything needed to do scientific computing

  • Numpy - for array manipulations
  • Scipy - Scientific library
  • Matplotlib - for plotting
  • mpi4py - Wraps MPI
  • scikit-learn - machine learning and data mining
  • +++

More than 1,500,000 downloads

https://anaconda.org

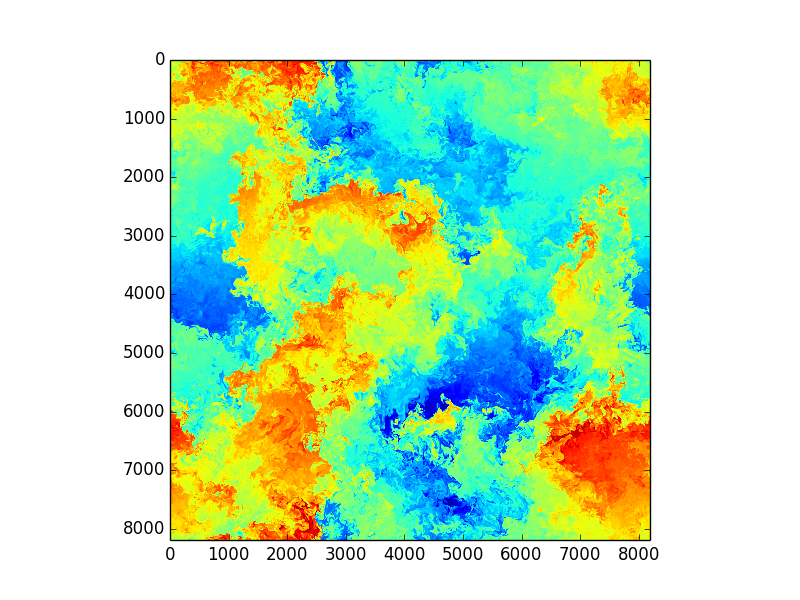
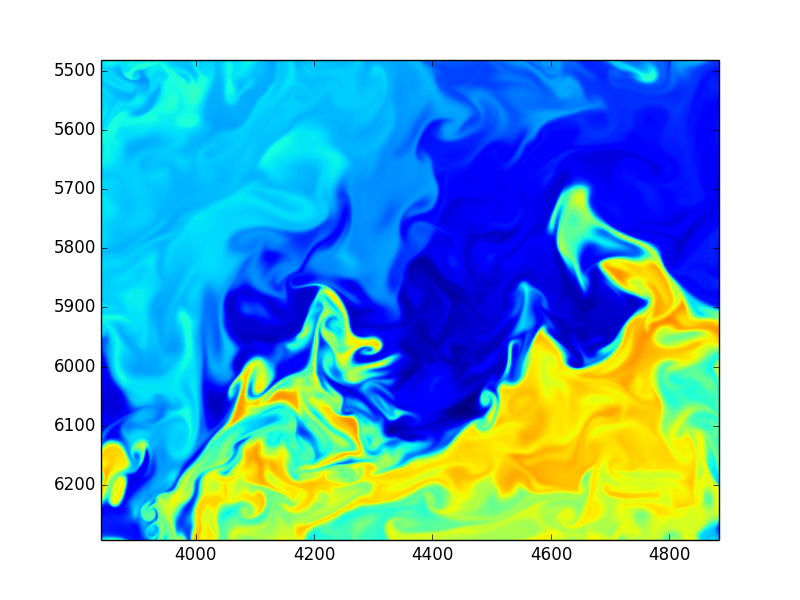
Using Fourier transformed Navier Stokes equations

Direct Numerical Simulations (DNS) of turbulence are traditionally performed with low-level Fortran or C

8192^3 \text{ mesh}

Part I: Python in high performance computing

Would it be possible to write a competitive, state of the art turbulence solver in Python?

From scratch?

(Not just wrapping a Fortran solver)

Using only standard Python modules numpy/scipy/mpi4py?

Can this solver be made to run on thousands of cores ?

With billions of unknowns?

As fast as C/fortran?

What does it take to build a spectral DNS solver?

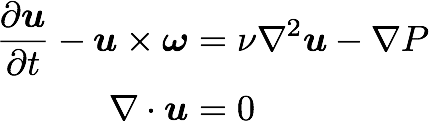
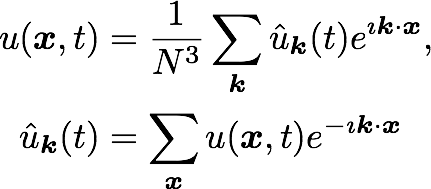
Triply periodic domain

Fourier space

[0, 2 \pi]^3

Equations:

What does it take to build a spectral DNS solver?

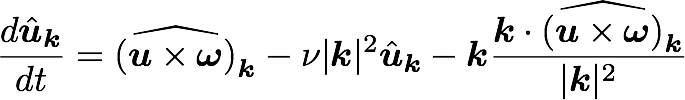
Navier Stokes in spectral (Fourier) space:

Pseudo-spectral treatment of nonlinearity

Some timestepping routine (e.g., 4th order Runge-Kutta)

Classical pseudo-spectral Navier-Stokes solver

The kind that has been used to break records since the day of the first supercomputer

What does it really take to implement a spectral DNS solver?

Numpy is designed around structured arrays that can be reshaped, resized, sliced, transposed, etc. 

Most array operations are performed in C and are very fast

  (1)  Structured grid

  (2)  3D parallel FFT

Numpy wraps FFTpack

pyFFTW wraps FFTW

MPI ?

But MPI for Python ( mpi4py, Lisandro Dalcin) wraps almost  the entire MPI library and is as efficient as low-level C

Implementation

A few computational details

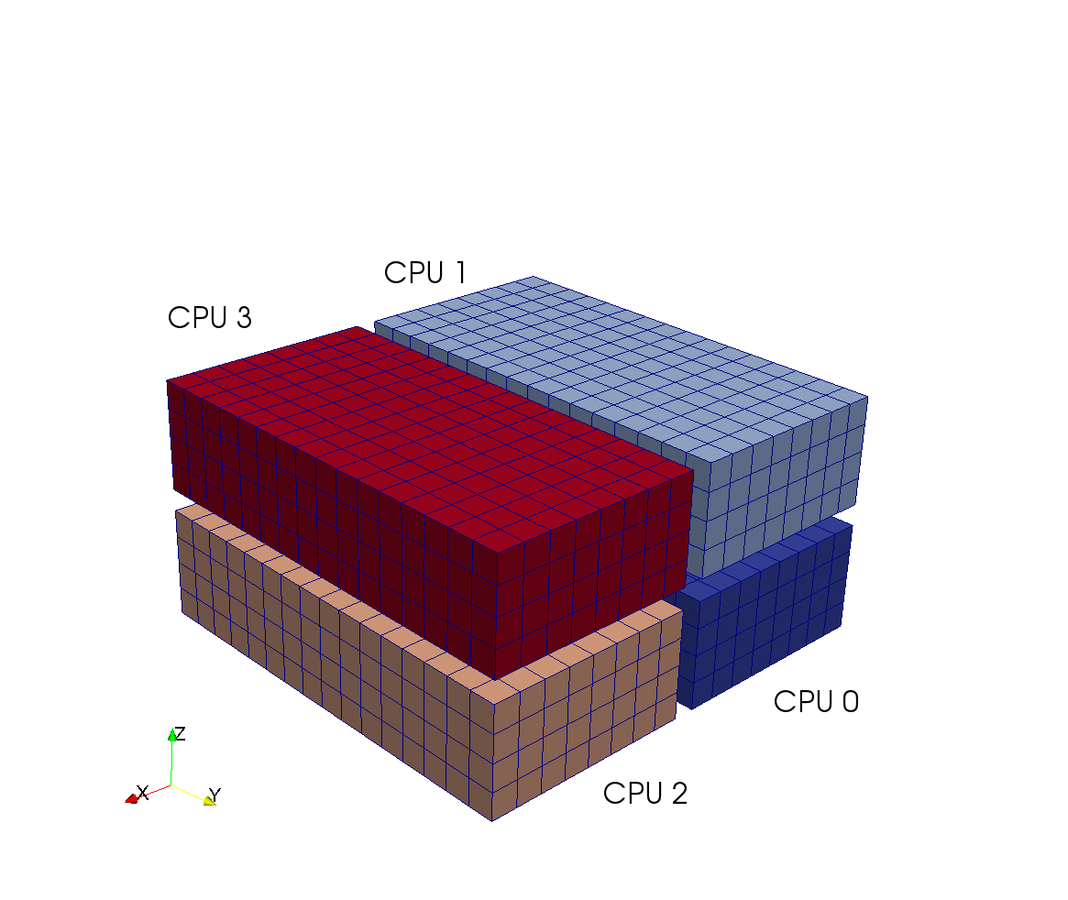
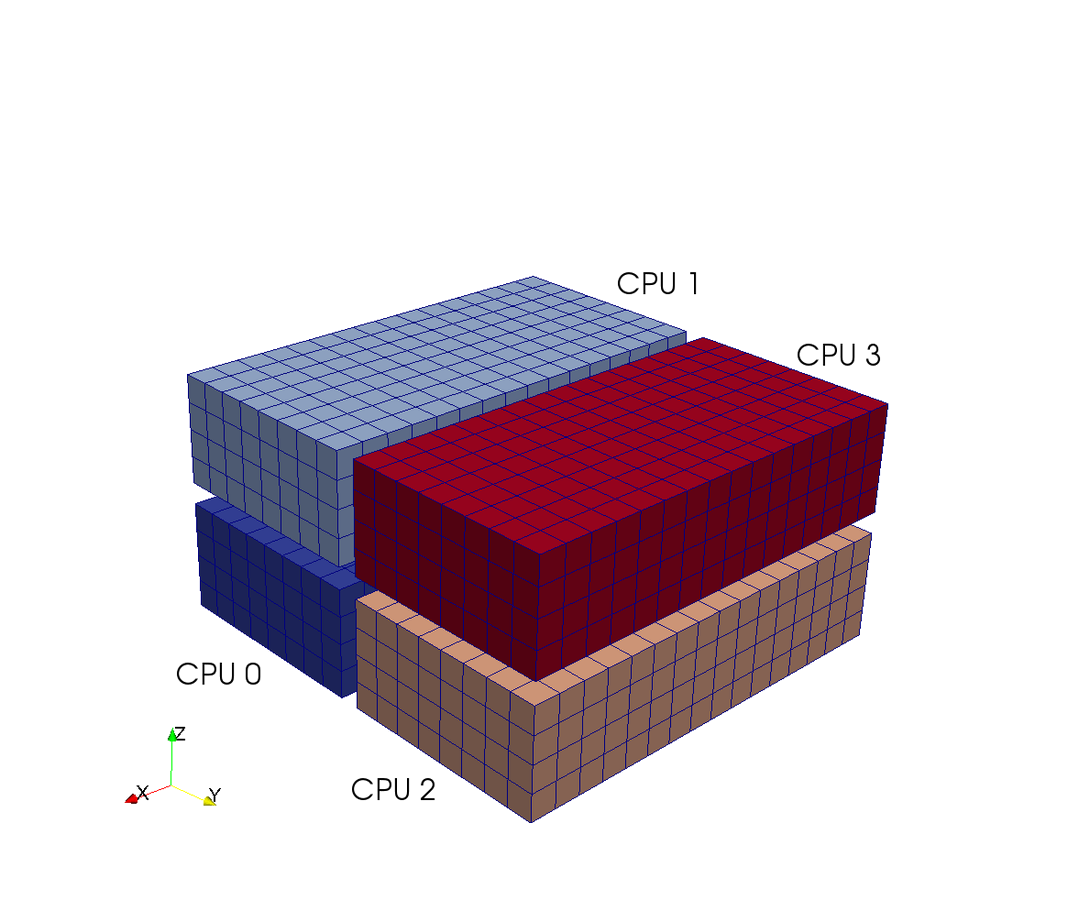
A computational box (mesh) needs to be distributed between a large (possibly thousands) number of processors 

N^3, N \sim 1000 - 10000

Mesh size:

Pencil 

Slab

\le N^2

CPUs

\le N

CPUs

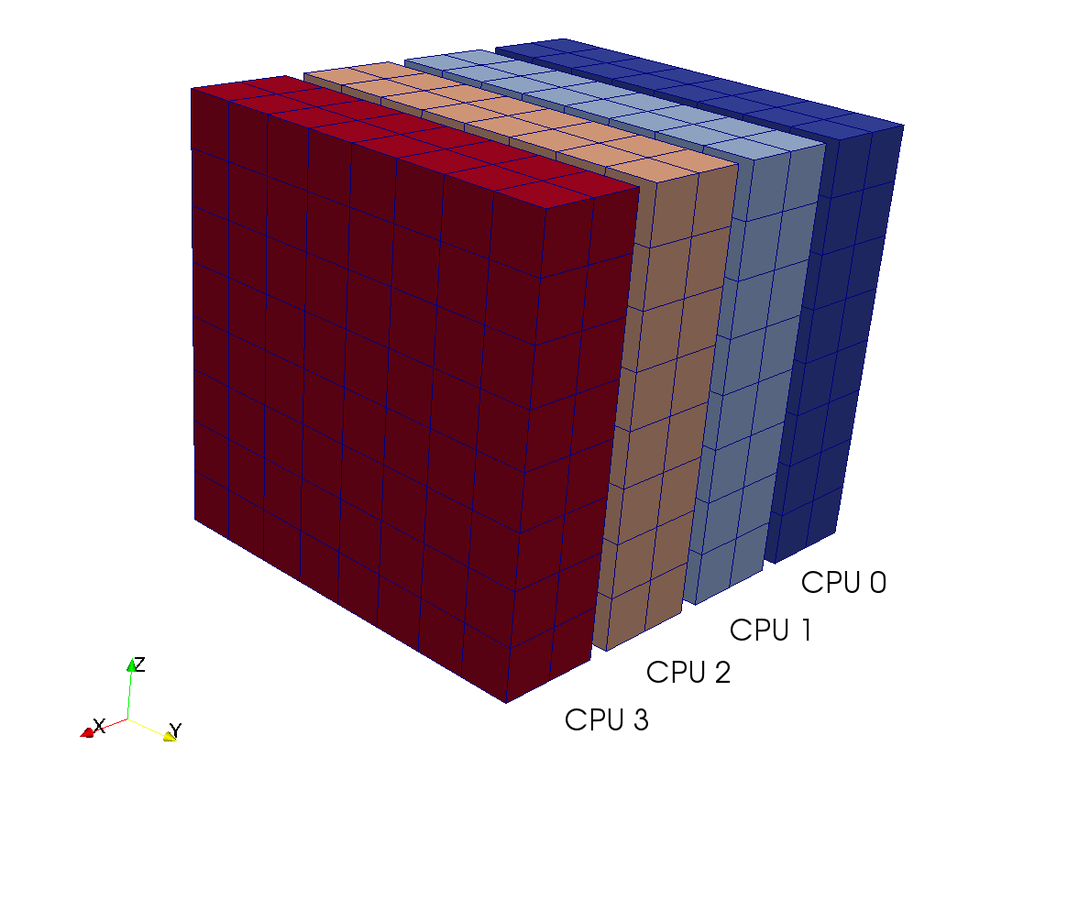
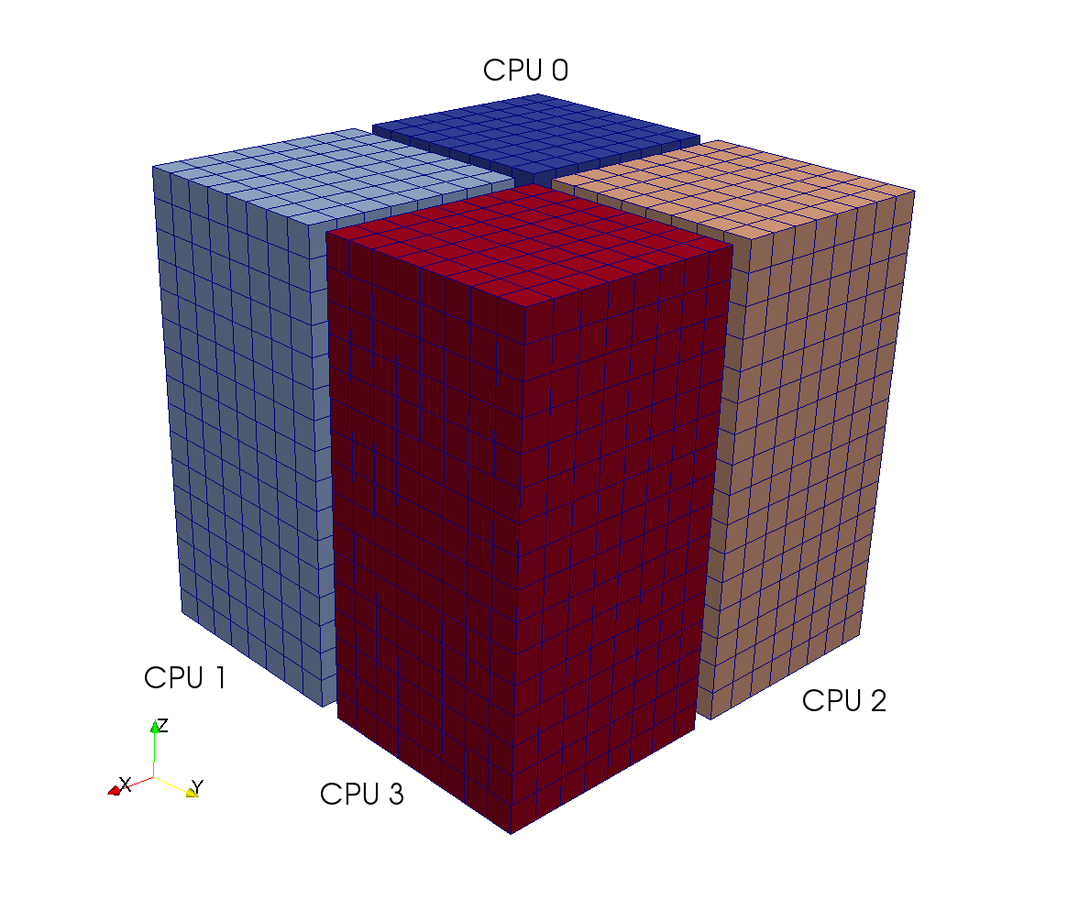
3D FFT with MPI

in a nutshell

real FFT in z, complex in y

 

No MPI required

Transpose and distribute

Then FFT in last direction

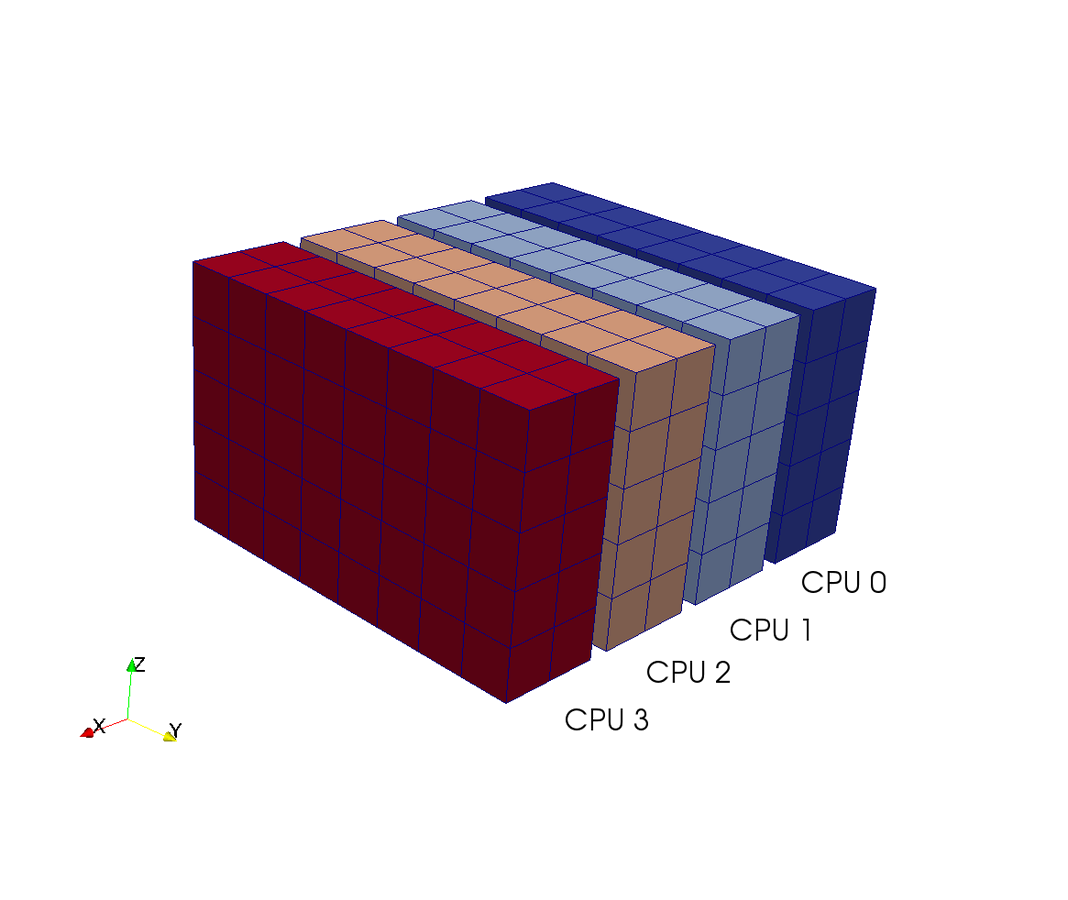
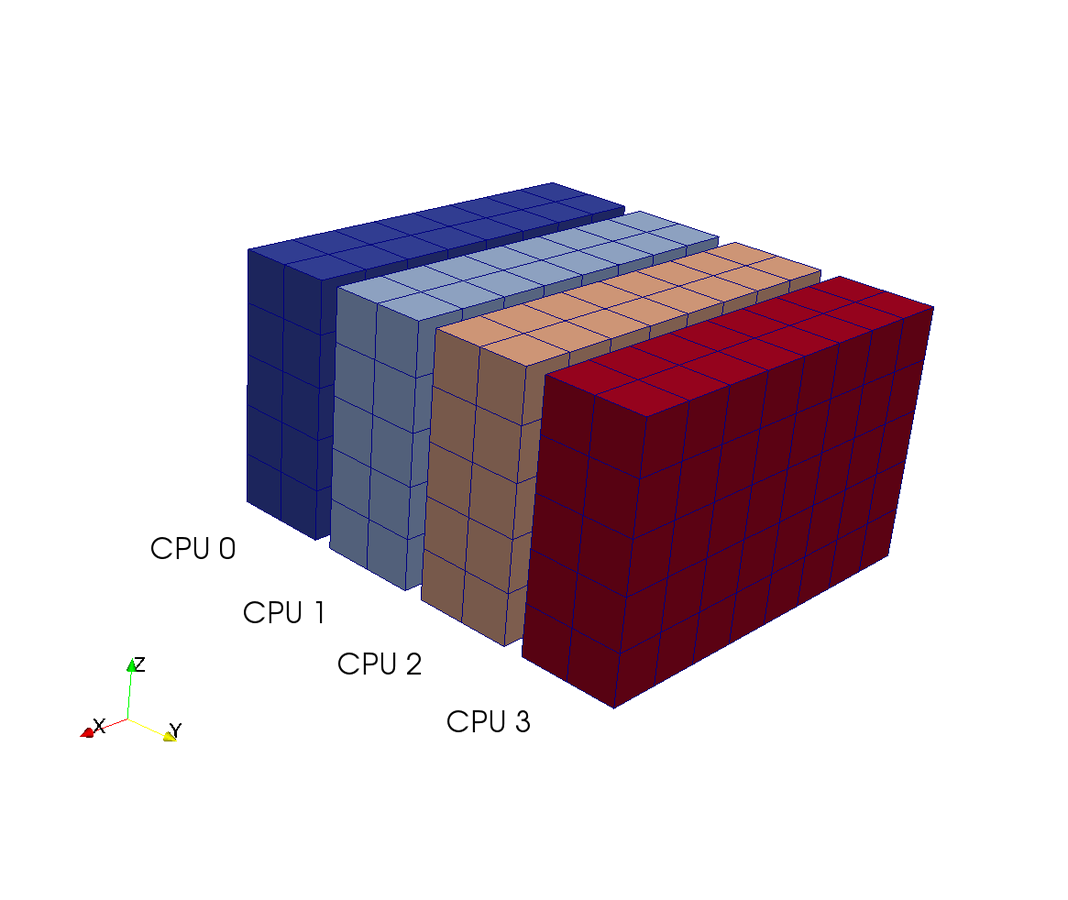
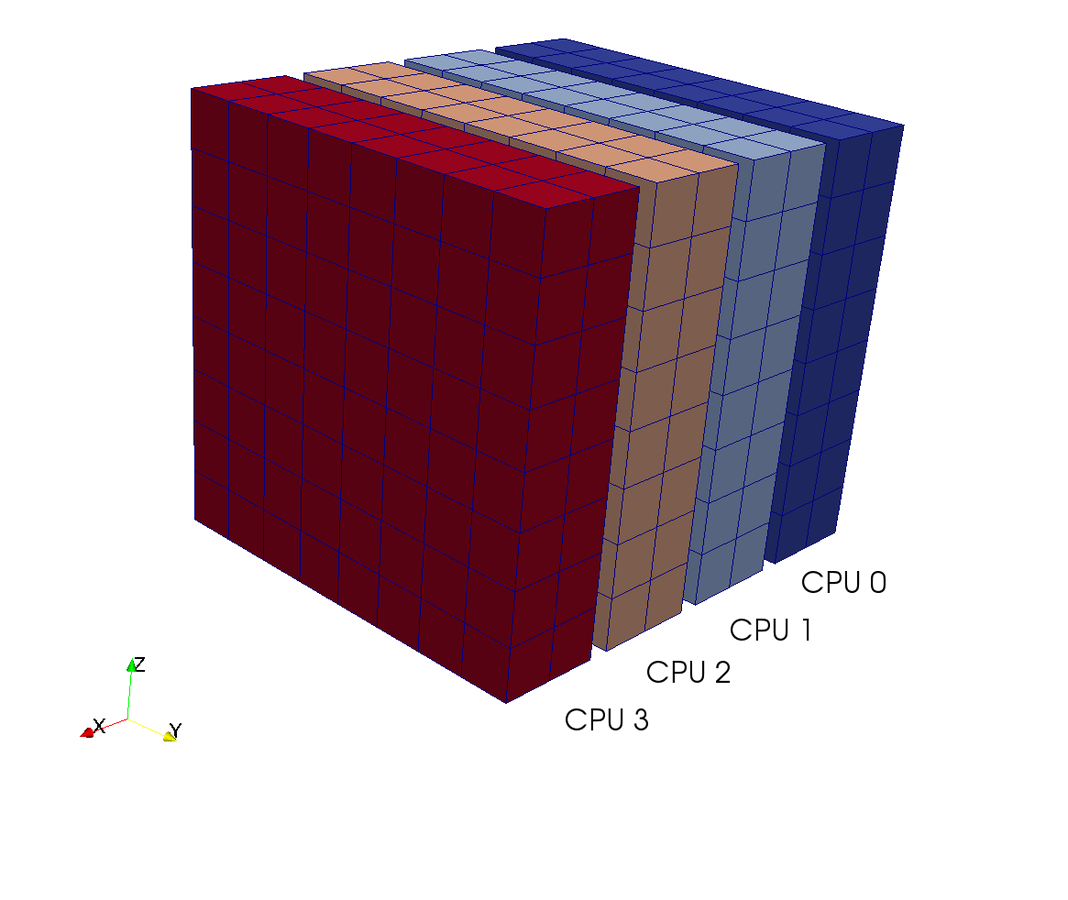
  1. 2D FFTs in Y-Z planes (local)
  2. transpose operation
  3. distribute data (MPI Alltoall)
  4. FFT in X-direction

What does it really take?

4 operations, four lines of Python code!

Pencil decomposition

in a nutshell

rfft(u, axis=2)

Transform

fft(u, axis=0)

Transform

 

fft(u, axis=1)

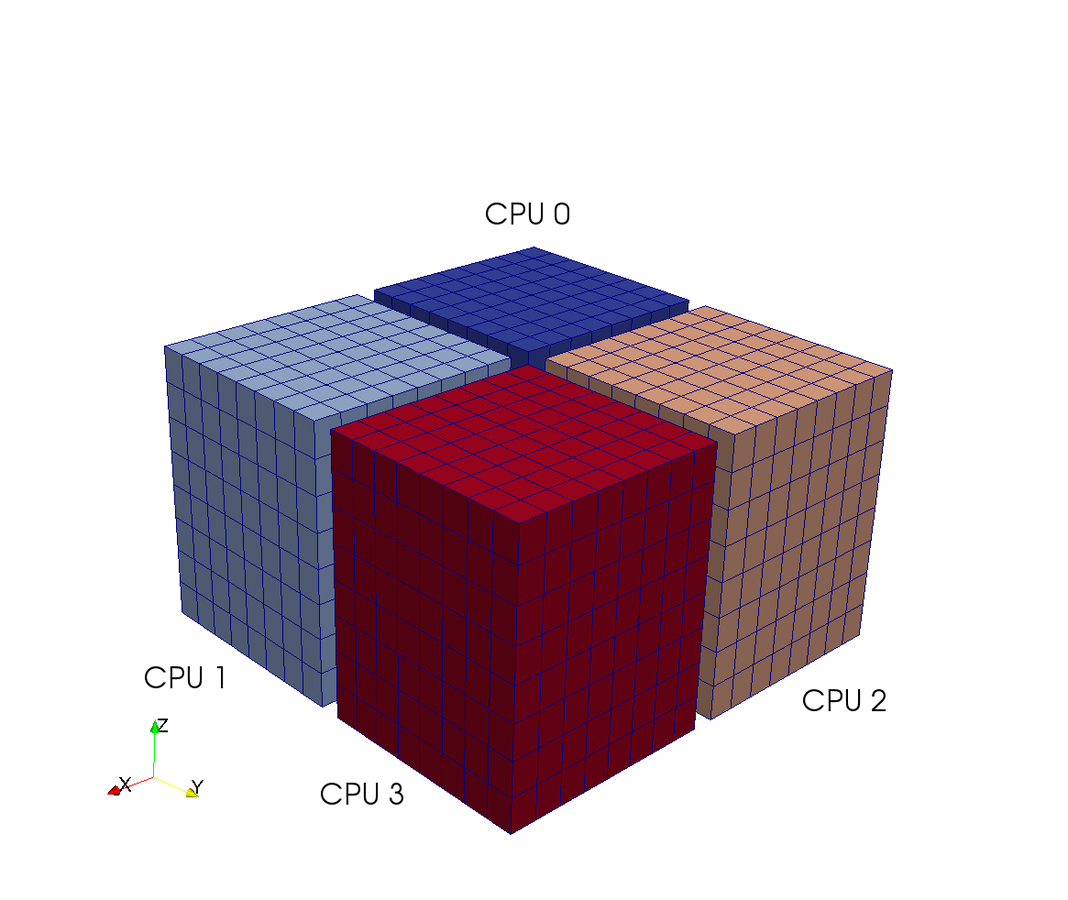
7 operations

  1. FFT z-dir​

  2. transpose

  3. communicate

  4. FFT y-dir

  5. transpose

  6. communicate

  7. FFT x-dir

7 lines of code!

With parallel 3D FFT we may develop parallel DNS solvers 

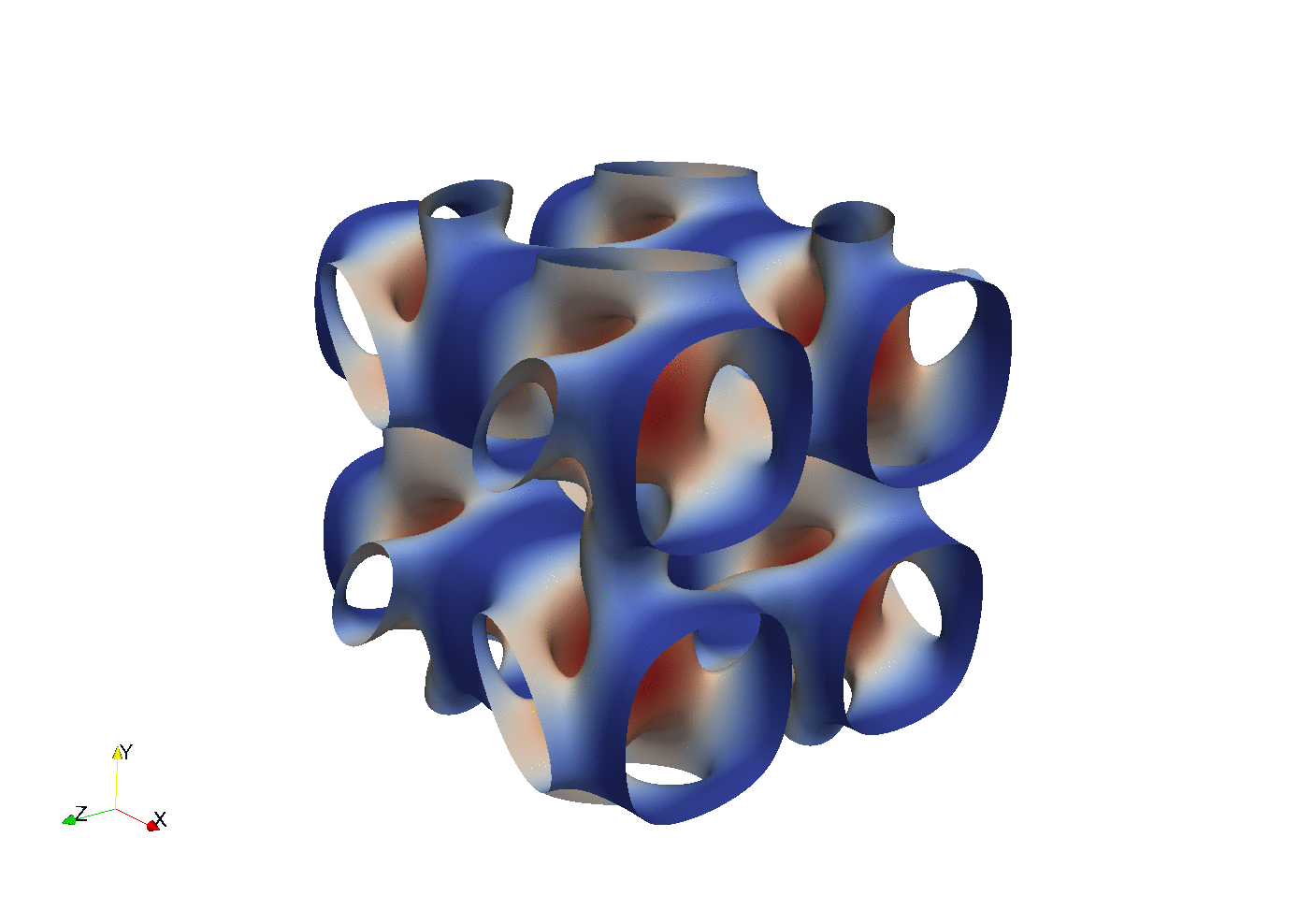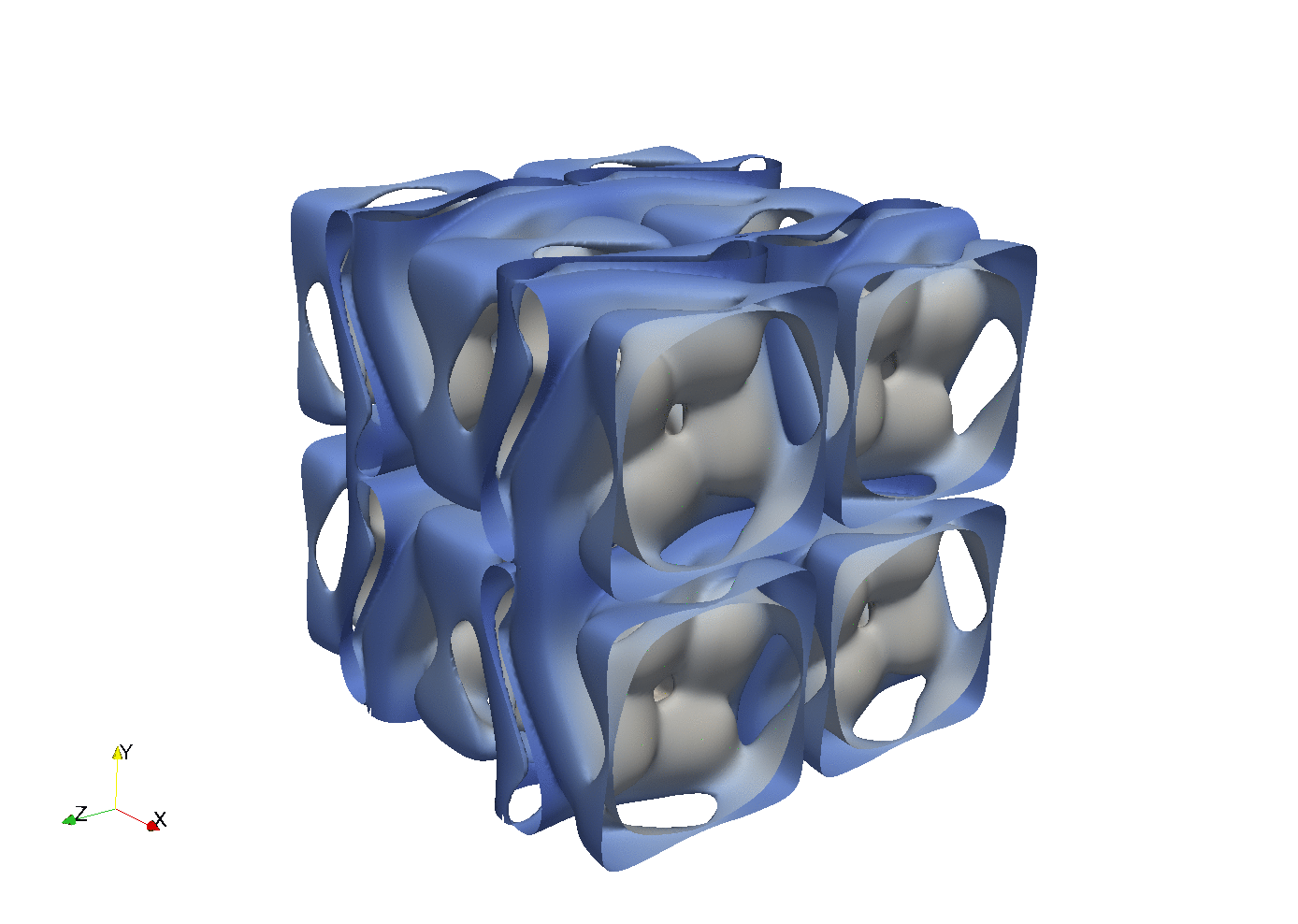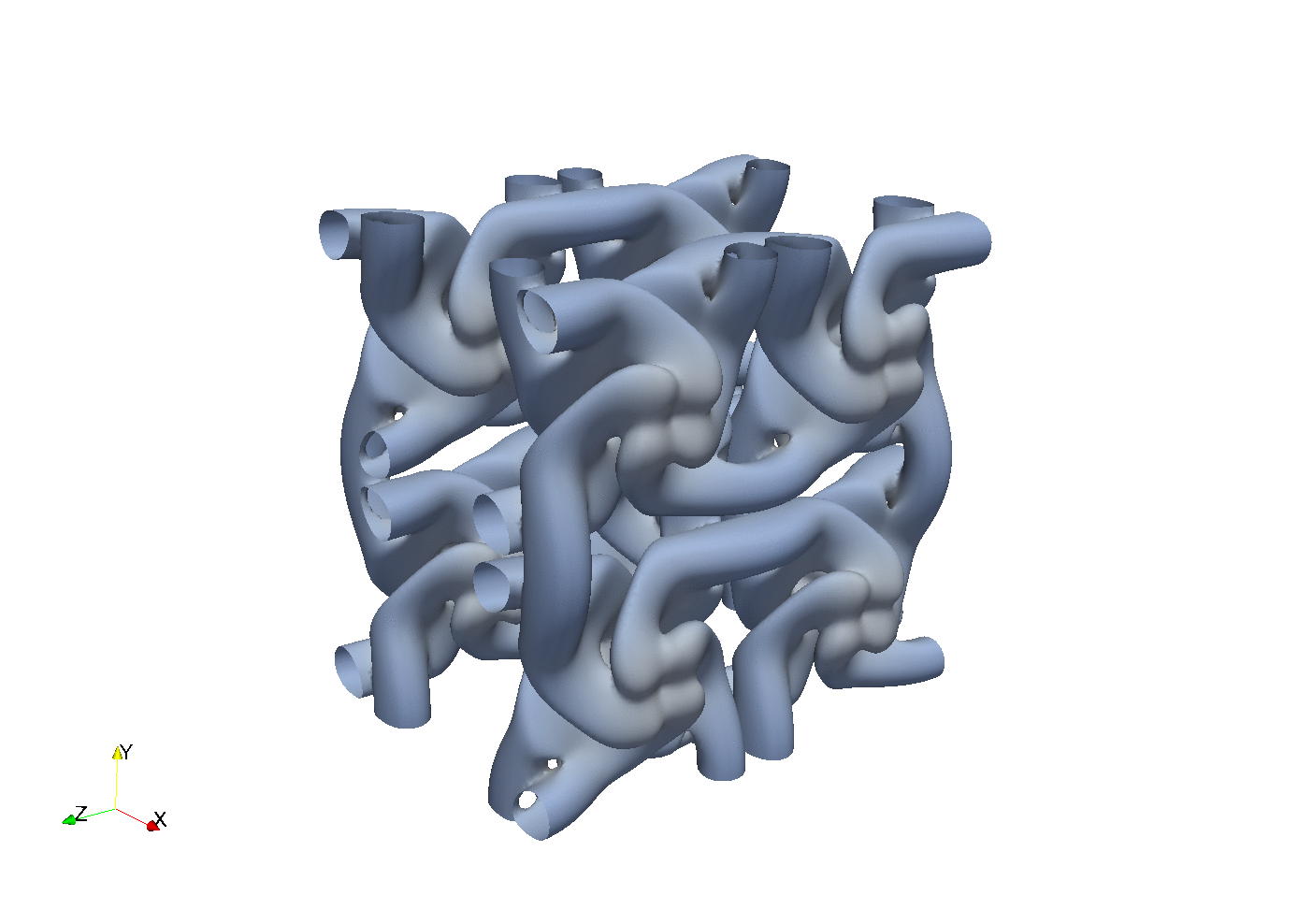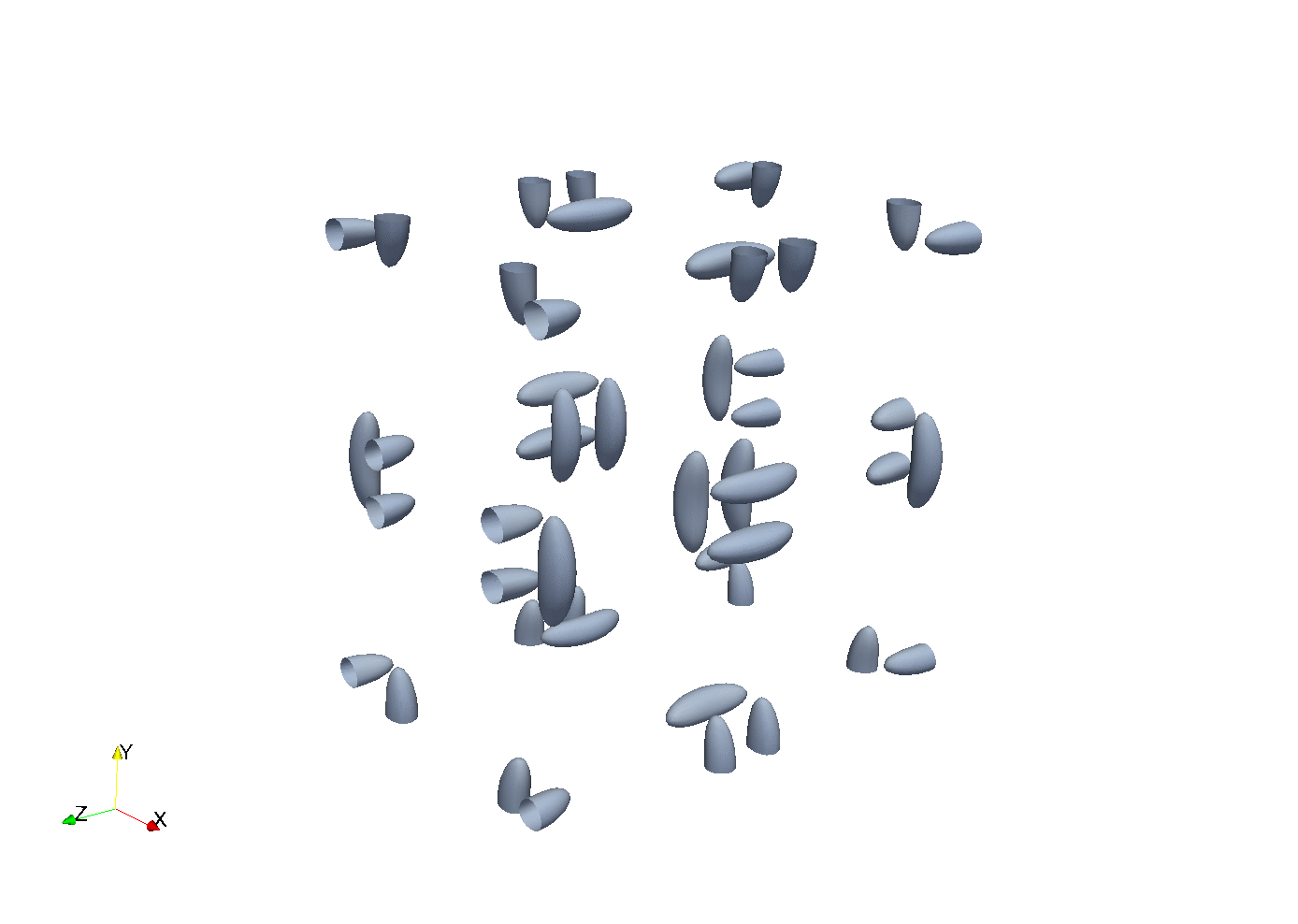
Enstrophy colored by pressure

and

100 lines of compact Python code is enough to implement

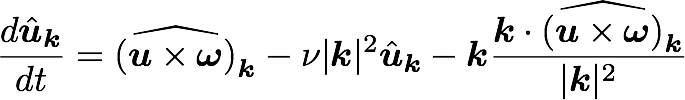
Ok, so it was relatively easy to implement

How about speed and parallel scaling?

Can we compete with low-level C/C++ or Fortran on supercomputers?

Parallell scaling

Shaheen Blue Gene P supercomputer at KAUST Supercomputing Laboratory

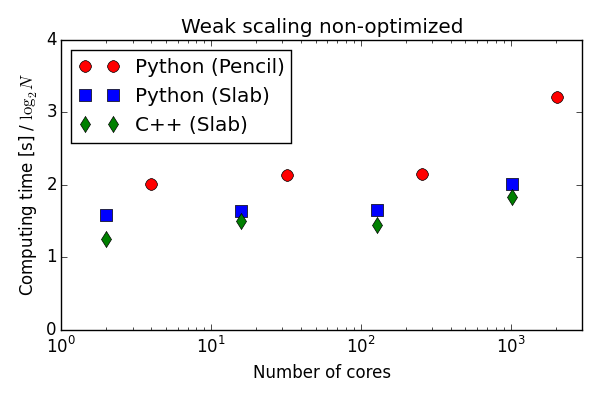
Testing the 100 lines of pure Python code in parallel

C++(slab) 20-30 % faster than Python (slab)

Good strong scaling

mesh = 

2048^3
512^3

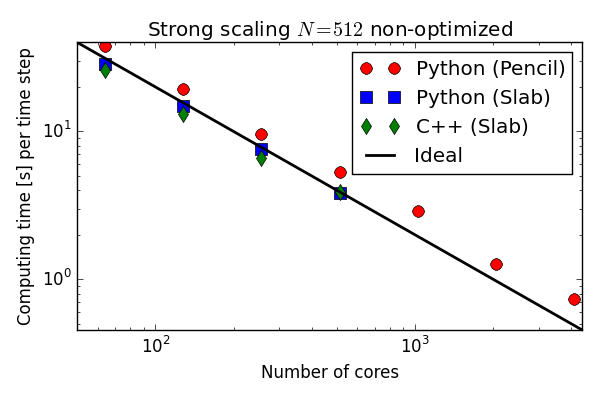
Why slower than C++?

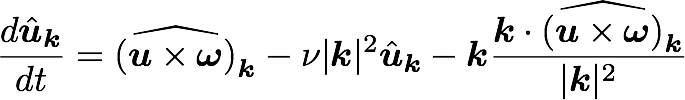
Actually, the numpy ufuncs used to compute the cross product is the main reason

Luckily Python has several options for optimizing slow code

Moving cross product to Cython or Numba

def cross(a, b, c):
    c[0] = a[1]*b[2]-a[2]*b[1]
    c[1] = a[2]*b[0]-a[0]*b[2]
    c[2] = a[0]*b[1]-a[1]*b[0]
    return c

u = np.ones((3, N, N, N))
w = np.ones((3, N, N, N))
v = np.zeros((3, N, N, N))
v = cross(u, w, v)

Numpy has to create intermediate work arrays on the fly

Hardcoding the cross product into one single loop

@jit(float[:,:,:,:](float[:,:,:,:], float[:,:,:,:], float[:,:,:,:]), nopython=True)
def cross(a, b, c):
    for i in xrange(a.shape[1]):
        for j in xrange(a.shape[2]):
            for k in xrange(a.shape[3]):
                a0 = a[0,i,j,k]
                a1 = a[1,i,j,k]
                a2 = a[2,i,j,k]
                b0 = b[0,i,j,k]
                b1 = b[1,i,j,k]
                b2 = b[2,i,j,k]
                c[0,i,j,k] = a1*b2 - a2*b1
                c[1,i,j,k] = a2*b0 - a0*b2
                c[2,i,j,k] = a0*b1 - a1*b0
    return c

Either Cython or Numba will do the trick. A few lines more

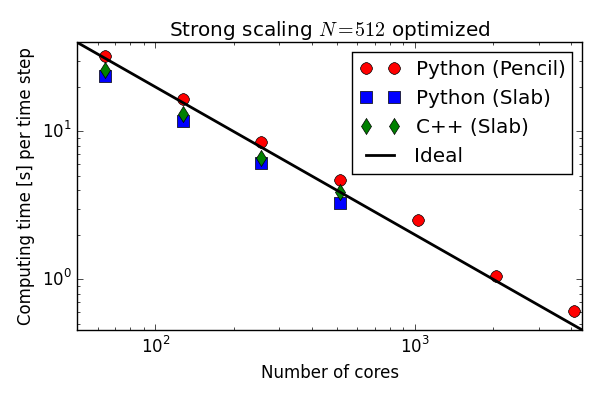
Numba and Cython perform approximately the same

and as fast as C++!

Approximately 5 times faster than original

Solver optimized with Cython

More than matches C++ on the Blue Gene P!

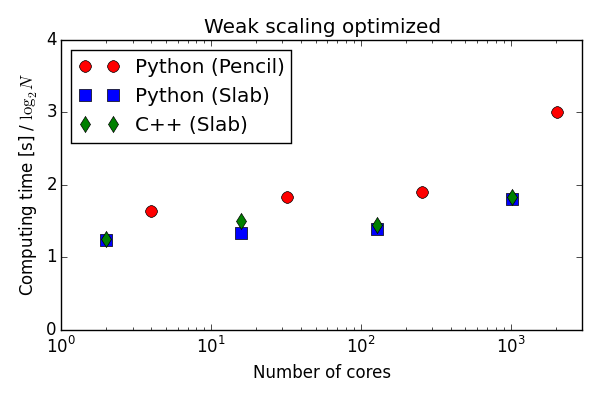
On an even larger supercomputer

64^3

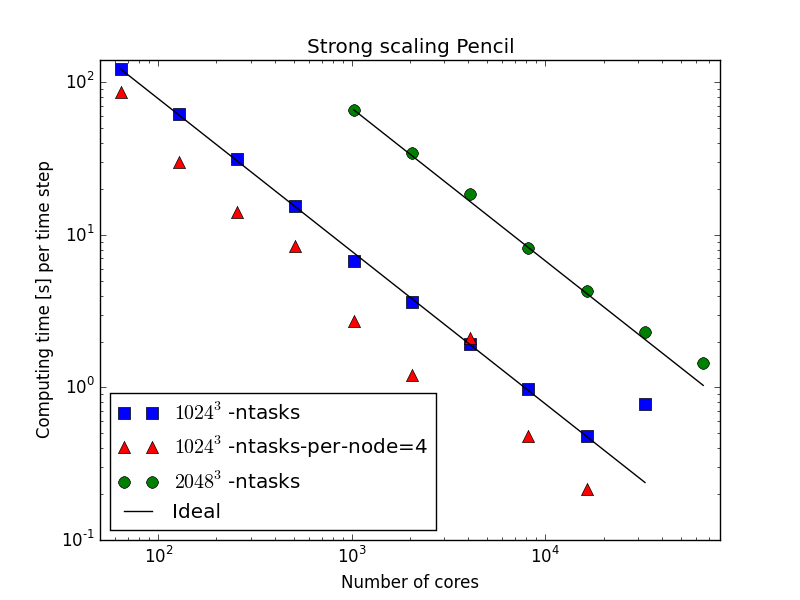
mesh size =         per task

65536 tasks!

mesh =    

per task

Word of warning

2048 nodes, or 65536 tasks, take about 13 minutes to load Python and get started

0.5 \cdot 64^3

Concept proven

Python can be used for high performance supercomputing and it can be used for DNS with Fourier

mpi4py-fft

https://bitbucket.org/mpi4py/mpi4py-fft

With Lisandro Dalcin at KAUST

~ 500 lines of  Python code

With the newly released

we can do any transform from FFTW in parallel

Highly configurable and fast

Part II of talk

Automating the spectral Galerkin method

on non-periodic domains, with different types

of boundary conditions (Dirichlet/Neumann)

Not just periodic Fourier

With a highly configurable library for any fast transforms

we can now implement the spectral Galerkin method

The spectral Galerkin method

Galerkin meets orthogonal

global spectral basis functions, e.g.

  • Chebyshev
  • Legendre
  • Fourier
\left( u, v \right)_w = \int_{\Omega} u\, v^* \, w\, dx
u(x) = \displaystyle\sum_{k=0}^{N-1} \hat{u}_k \phi_k(x)

Solution

Expansion coefficients

(unknowns)

Global basis functions

We use it to solve PDEs using the method of weighted residuals

Weighted inner products:

The spectral Galerkin method

works in three steps

  1. Choose global basis (test) functions satisfying the correct boundary conditions. Usually modified Chebyshev or Legendre polynomials, or Fourier exponentials

  2. Transform PDEs to weak variational forms using the method of weighted residuals

  3. Assemble and solve linear system of equations

Spectral Galerkin

Poisson example

\nabla^2 u(x) = f(x) \quad \text{for} \quad x \in [-1, 1]
u(\pm 1) = 0

1) Create a basis that satisfies boundary conditions, e.g.,

\phi_k(x) = L_k(x) - L_{k+2}(x) \quad V = \text{span}\{\phi_k\}_{k=0}^{N-3}
\displaystyle \int_{-1}^{1}v \nabla^2 u \, w dx = \int_{-1}^{1} vf w dx
\text{where } w(x) \text{ is a weight function and } u \in V \text{ is trial function}

(Legendre polynomial order k+2)

2) Transform PDE to variational form using test function  

v \in V

3) Assemble and solve linear system of equations

\text{Find } u \in V, \text{such that}
\left(v, \nabla^2 u \right)_w^N = \left(v, f \right)_w^N \quad \forall v \in V
\left( v, u\right)_w^N \approx \displaystyle \int_{-1}^{1} vu^* w dx
u(x) = \displaystyle\sum_{j=0}^{N-1} \hat{u}_j \phi_j(x)
v(x) = \phi_k(x)

Trial function

Test function

With quadrature notation

\left( \phi_k, \sum_j \hat{u}_j \phi_j^{''} \right)_w^N = \left( \phi_k, f\right)_w^N
A_{kj} \hat{u}_j = \tilde{f}_k

Insert to get linear algebra problem:

A_{kj} = \left( \phi_k, \phi_j^{''} \right)_w^N

With

3 steps - Sounds generic and easy?

Let's automate!

from fenics import *

mesh = UnitSquareMesh(8, 8)
V = FunctionSpace(mesh, 'CG', 1)

# Define variational problem
u = TrialFunction(V)
v = TestFunction(V)
f = Constant(-6.0)
a = inner(grad(u), grad(v))*dx
L = f*v*dx
  • Automates the finite element method (Galerkin)
  • Code very similar to mathematics
  • Basis functions with local support

  • Finite accuracy (not spectral)

How?

\int_{\Omega} \nabla u \cdot \nabla v dx

Shenfun

https://github.com/spectralDNS/shenfun

Python package (~3k loc) for automating the spectral Galerkin

method for high performance computing on tensor product grids

  • A FEniCS like interface with a simple form language
  • MPI - invisible to the user: mpi4py-fft 
  • Fourier - Chebyshev - Legendre modified basis functions
  • Extremely fast (!), order optimal, direct solvers for Poisson, Helmholtz and Biharmonic problems

Shenfun implementation of 1D Poisson problem

import numpy as np
from shenfun import TestFunction, TrialFunction, inner, div, grad, chebyshev

N = 20
V = chebyshev.ShenDirichletBasis(N, plan=True)
v = TestFunction(V)
u = TrialFunction(V)

# Assemble stiffness matrix
A = inner(v, div(grad(u)))

# Some consistent right hand side
f = Function(V, False)
f[:] = -2

# Assemble right hand side
f_hat = inner(v, f)

# Solve equations and transform spectral solution to real space
f_hat = A.solve(f_hat)
fj = V.backward(f_hat)

x = V.mesh(N)
assert np.allclose(fj, 1-x**2)

Very similar to FEniCS!

just with spectral accuracy

(1) Create basis

(2) Variational forms

(3) Solve system

2D/3D/4D..  Tensor product spaces

Cartesian products of Fourier and Chebyshev/Legendre bases

u(x,y,z,t) = \displaystyle \sum_{k}\sum_{l}\sum_{m} \hat{u}_{klm}(t) \phi_k(x)\phi_l(y)\phi_m(z)
W(x,y,z) = V(x) \times V(y) \times V(z)

Any Cartesian combination of spaces (ultimately)

With solutions of the form:

Unknown expansion coefficients

Tensor product spaces

Implementation

from shenfun import *
from mpi4py import MPI

comm = MPI.COMM_WORLD
N = (20, 30)

# Create two bases
V0 = chebyshev.ShenDirichletBasis(N[0])
V1 = fourier.R2CBasis(N[1])

# Create tensor product space
T = TensorProductSpace(comm, (V0, V1))
v = TestFunction(T)
u = TrialFunction(T)

A = inner(v, div(grad(u)))

# Or 3D
V2 = fourier.C2CBasis(40)
T3 = TensorProductSpace(comm, (V0, V2, V1))
v = TestFunction(T3)
u = TrialFunction(T3)

A = inner(v, div(grad(u)))

MPI under the hood

using mpi4py-fft

on tensor product grids like:

Slab

Pencil

A simple form language

influenced heavily by UFL/FEniCS

Mathematical operators act on test, trial, or functions with data 

V = TensorProductSpace(comm, (V0, V1, V2))

# Form arguments:
v = TestFunction(V)
u = TrialFunction(V)
u_ = Function(V, False)

# Forms
du = grad(u_)
d2u = div(du) 
cu = curl(du)
dudx = Dx(u_, 0)

Inner products and projections

A = inner(v, u)    # Bilinear form, assembles to matrices
f = inner(v, u_)   # Linear form, assembles to vector
project(div(grad(u_)), V)  # projection to V

Fast transforms

u_hat = V.forward(u, u_hat)        u = V.backward(u_hat, u)

Move back and forth between         and        using fast transforms

Periodic basis using fast Fourier transforms

Non-periodic basis using fast Chebyshev transforms (not for Legendre)

\blue{u}
\blue{\hat{u}}
\blue{u}(x,y,z) = \displaystyle\sum_{k=0}^{N-1} \sum_{l=0}^{N-1} \sum_{m=0}^{N-1} \blue{\hat{u}_{klm}} \phi_k(x)\phi_l(y)\phi_m(z)

Nonlinearities

all treated with pseudo-spectral techniques

u \times \nabla \times u
u \cdot u
u | u |^2

(1) Compute inverse 

u = T.backward(u_hat)

with dealiasing using

3/2-rule (padding) or 2/3-rule

(3) Transform back to spectral space 

w = u*u

(2) Compute nonlinearity 

w_hat = T.forward(w)
T = TensorProductSpace(comm, (V0, V1, V2))

Fast direct solvers

1D: \text{Find } u \in V, \text{such that}
\left(v, \nabla^2 u \right)_w^N = \left(v, f \right)_w^N \quad \forall v \in V
A_{kl} \hat{u}_l = \tilde{f}_k
\text{Leading to a linear algebra problem:}

Fourier: A is diagonal

Modified Legendre: A is diagonal

Modified Chebyshev: A sparse  - solved as tridiagonal matrix

Fast direct solvers

2 dimensions

\left(v, \nabla^2 u \right)_w^N = \left(v, f \right)_w^N \quad \forall v \in V^1\times V^2
\text{Find } u \in V^1\times V^2, \text{such that}
A_{km}^1 B^2_{nl}\hat{u}_{mn} + B^1_{km} A^2_{nl} \hat{u}_{mn} = \tilde{f}_{kl}

Matrix form:

A^1 \hat{u} B^2 + B^1 \hat{u} (A^{2})^T = \tilde{f}

Sparse matrices A (stiffness) and B (mass) are 1D matrices of basis (1/2)

Very fast direct solvers implemented in parallel using matrix decomposition method

Linear algebra:

2D Poisson

in more detail

\nabla^2 u(x) = f(x) \quad \text{for} \quad x \in [0, 2\pi] \times [-1, 1]
u(x, \pm 1) = 0 \quad u(2\pi, y) = u(0, y)
from shenfun import *
from mpi4py import MPI
comm = MPI.COMM_WORLD
N = (64, 64)
K1 = R2CBasis(N[0])
SD = chebyshev.bases.ShenDirichletBasis(N[1])
T = TensorProductSpace(comm, (K1, SD))
u = TrialFunction(T)
v = TestFunction(T)

2D Poisson

Assemble matrix

Trial function

Test function

\phi_l(x) = \exp(ilx)
\phi_m(y) = T_m(y) - T_{m+2}(y)

Combination of Chebyshev polynomials (or Legendre) that satisfies boundary conditions

Jie Shen's modified basis satisfies bcs and leads to very sparse matrices

u(x, y) = \displaystyle \sum_{k, j} \hat{u}_{kj} \phi_k(x) \phi_j(y)
v(x, y) = \phi_l(x) \phi_m(y)

2D Poisson

Assemble matrices

(-k^2 B_{mj}^D + A_{mj}^D)\hat{u}_{kj}\quad \forall \, k=0,1,\ldots, N-1

1D stiffness

1D mass

A_{lk}^{F} B_{mj}^{D}\hat{u}_{kj} + B_{lk}^{F} A_{mj}^{D} \hat{u}_{kj}

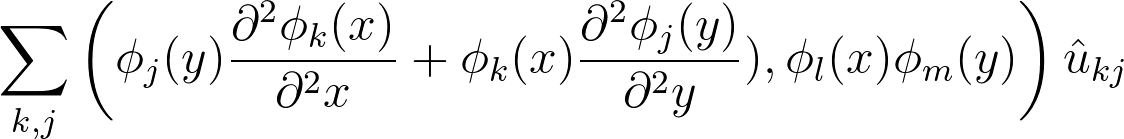
Matrix form

\text{Fourier matrices } B^F \text{ and } A^{F} \text{ are diagonal }
\text{and can be eliminated, leaving N 1D problems:}

2D Poisson

Assemble matrices in shenfun

from shenfun import *
from mpi4py import MPI
comm = MPI.COMM_WORLD
N = (64, 64)
K1 = R2CBasis(N[0])
SD = chebyshev.bases.ShenDirichletBasis(N[1])
T = TensorProductSpace(comm, (K1, SD))
u = TrialFunction(T)
v = TestFunction(T)

mat = inner(div(grad(u)), v)

Creates mat - a dictionary holding two sparse matrices: mass and stiffness. Fourier contribution are scales to matrices

(-k^2 B_{mj} + A_{mj})\hat{u}_{kj}\quad \forall k=0,1,\ldots, N-1

Complex Ginzburg-Landau

example

\frac{\partial u}{\partial t} = \nabla^2 u + u -(1+1.5i)u |u|^2


2D periodic (x, y) \( \in [-50, 50]^2 \)

Use Fourier in both directions

Weak form, only spatial discretization:

\frac{\partial (v, u)^N}{\partial t} = -(\nabla v, \nabla u)^N + (v, u -(1+1.5i)u |u|^2)^N
(2\pi)^2\frac{\partial \hat{u}}{\partial t} = -(\nabla v, \nabla u)^N + (v, u -(1+1.5i)u |u|^2)^N

Complex Ginzburg-Landau

example

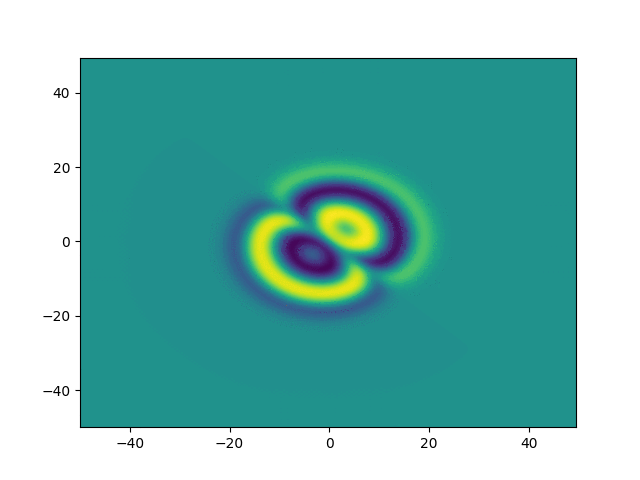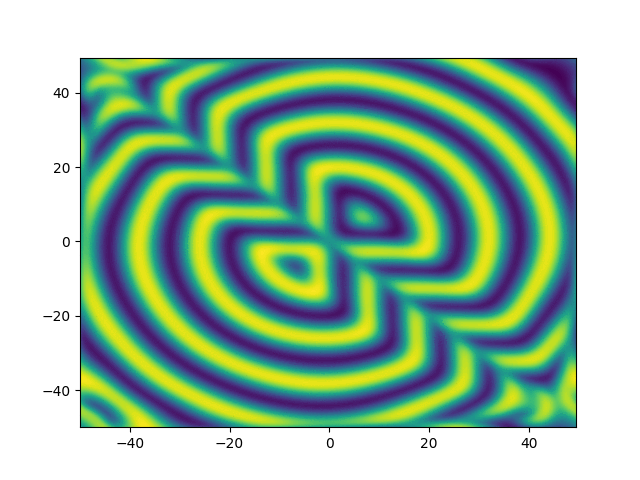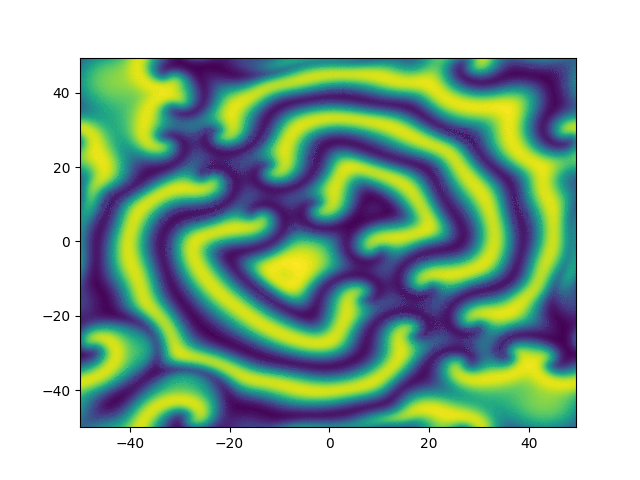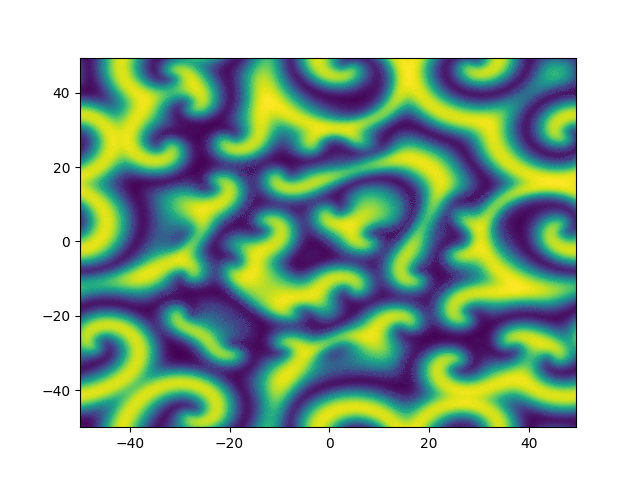
2D periodic (x, y) \( \in [-50, 50]^2 \)

import sympy
from shenfun.fourier.bases import R2CBasis, C2CBasis
from shenfun import inner, grad, TestFunction, TrialFunction, \
    Function, TensorProductSpace

# Use sympy to set up initial condition
x, y = sympy.symbols("x,y")
ue = (x + y)*sympy.exp(-0.03*(x**2+y**2))

N = (200, 200)
K0 = C2CBasis(N[0], domain=(-50., 50.))
K1 = C2CBasis(N[1], domain=(-50., 50.))
T = TensorProductSpace(comm, (K0, K1))
u = TrialFunction(T)
v = TestFunction(T)
U = Function(T, False)

def compute_rhs(rhs, u_hat, U, T):
    rhs = inner(grad(v), -grad(U), output_array=rhs, uh_hat=u_hat)
    rhs /= (2*np.pi)**2
    rhs += u_hat
    rhs -= T.forward((1+1.5j)*U*abs(U)**2, w0)
    return rhs

# And, e.g., Runge-Kutta integrator
#
#

Key code:

(2\pi)^2\frac{\partial \hat{u}}{\partial t} = -(\nabla v, \nabla u)^N + (v, u -(1+1.5i)u |u|^2)^N

Navier Stokes 

Turbulent channel flow

3D tensor product space

2 Fourier bases +

Modified Chebyshev bases for wall normal direction

Kim and Moin modified version of Navier-Stokes:

\mathcal{H}

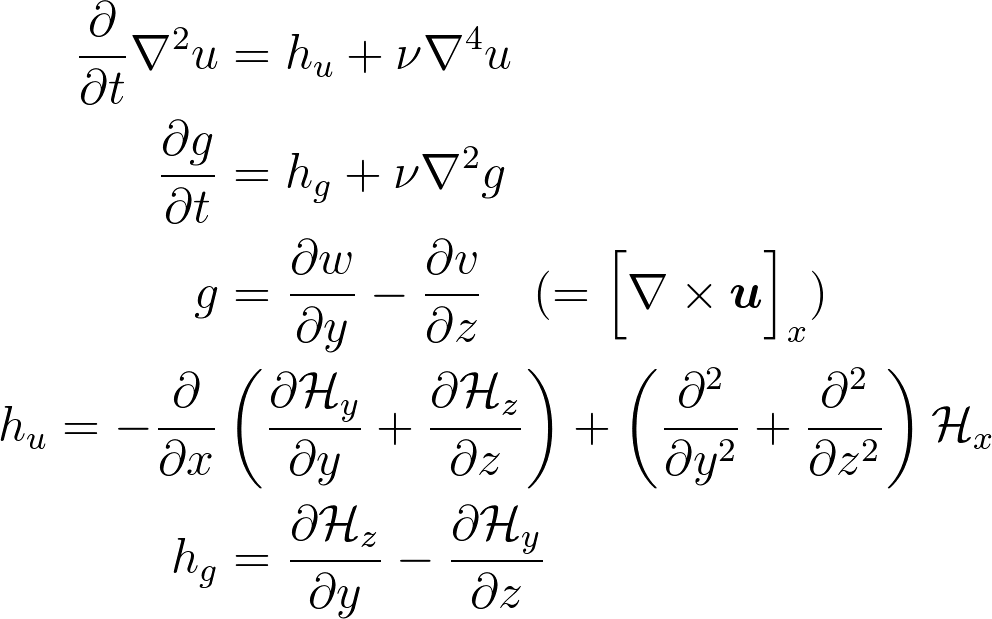
is convection

Wall normal velocity

Wall normal vorticity

Navier Stokes 

Turbulent channel flow

512\times 1024\times 1024

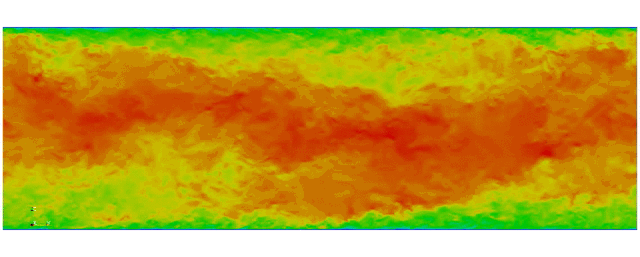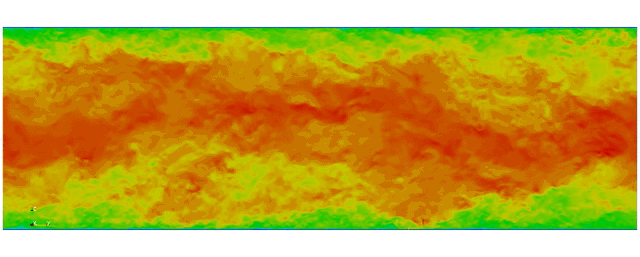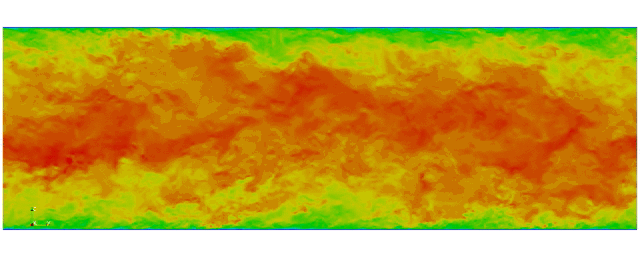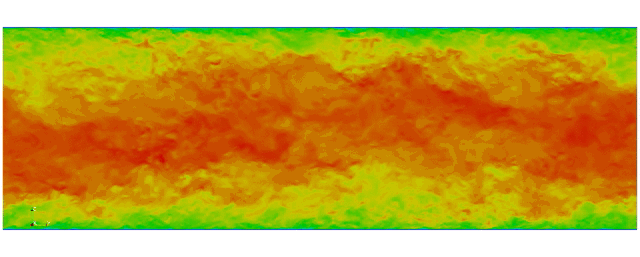
First fully spectral DNS with 

3D Tensor product mesh:

Shaheen II at KAUST

\text{Re}_{\tau} > 2000

Some more demos 

Thank you for your time! 

http://github.com/spectralDNS/shenfun

Questions?

conda install -c conda-forge -c spectralDNS shenfun

Made with Slides.com