Massively parallel implementation in Python of a pseudo-spectral DNS code for turbulent flows

Assoc. Professor Mikael Mortensen

Department of Mathematics, University of Oslo

Center for Biomedical Computing, Simula Research Laboratory

 

at EuroScipy 2015

Cambridge, UK, 28/8 - 2015

Direct Numerical Simulations of turbulence are performed with low-level Fortran or C

3D + time and HUGE resolution

Serious number crunching

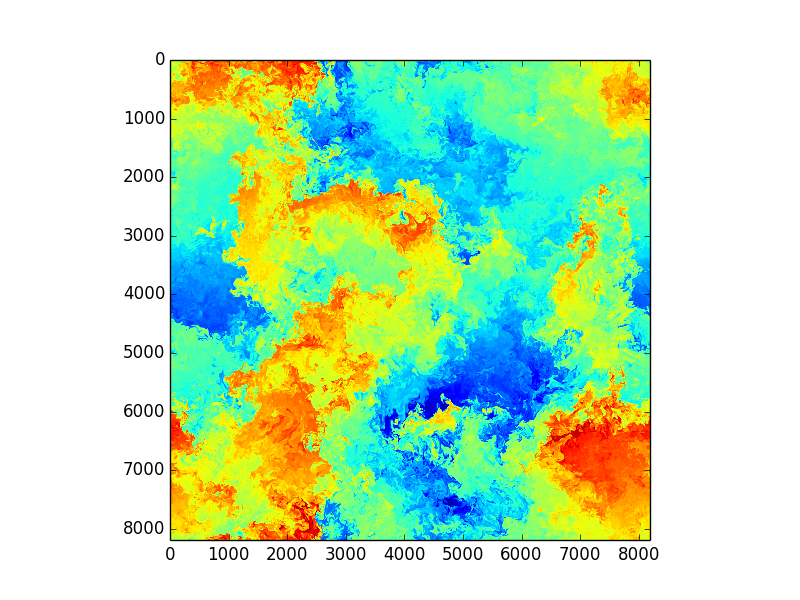
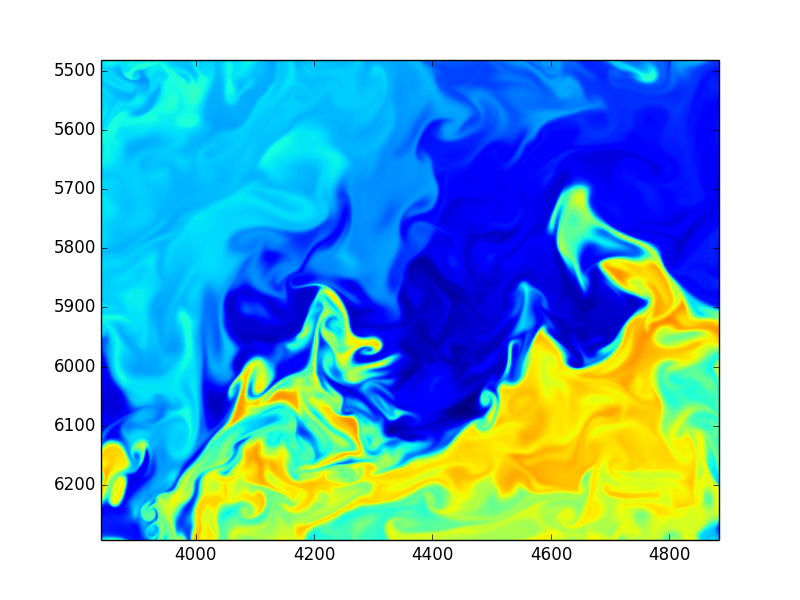
Images from huge DNS simulations by S. de Bruyn Kops, UmassAmherst, College of Engineering

Is it possible to write a competitive, state of the art turbulence solver in Python?

From scratch?

(Not just wrapping a Fortran solver)

Using only numpy/scipy/mpi4py?

Can this solver run on thousands of cores?

With billions of unknowns?

As fast as C?

 Turns out 100 lines of Python code can get you almost there!

Turbulence is governed by the Navier Stokes equations

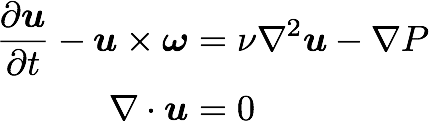
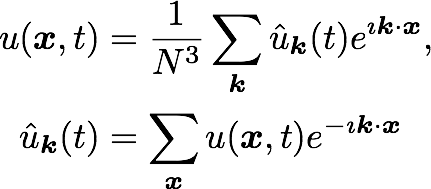
Triply periodic domain

Fourier space

Navier Stokes in spectral space

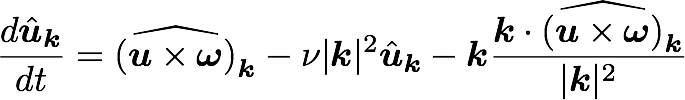
Eliminate pressure and solve ODEs:

Pseudo-spectral treatment of 

Explicit timestepping (4th order Runge-Kutta)

Classical pseudo-spectral Navier-Stokes solver

The kind that has been used to break records since the day of the first supercomputer

Implementation

A few computational details

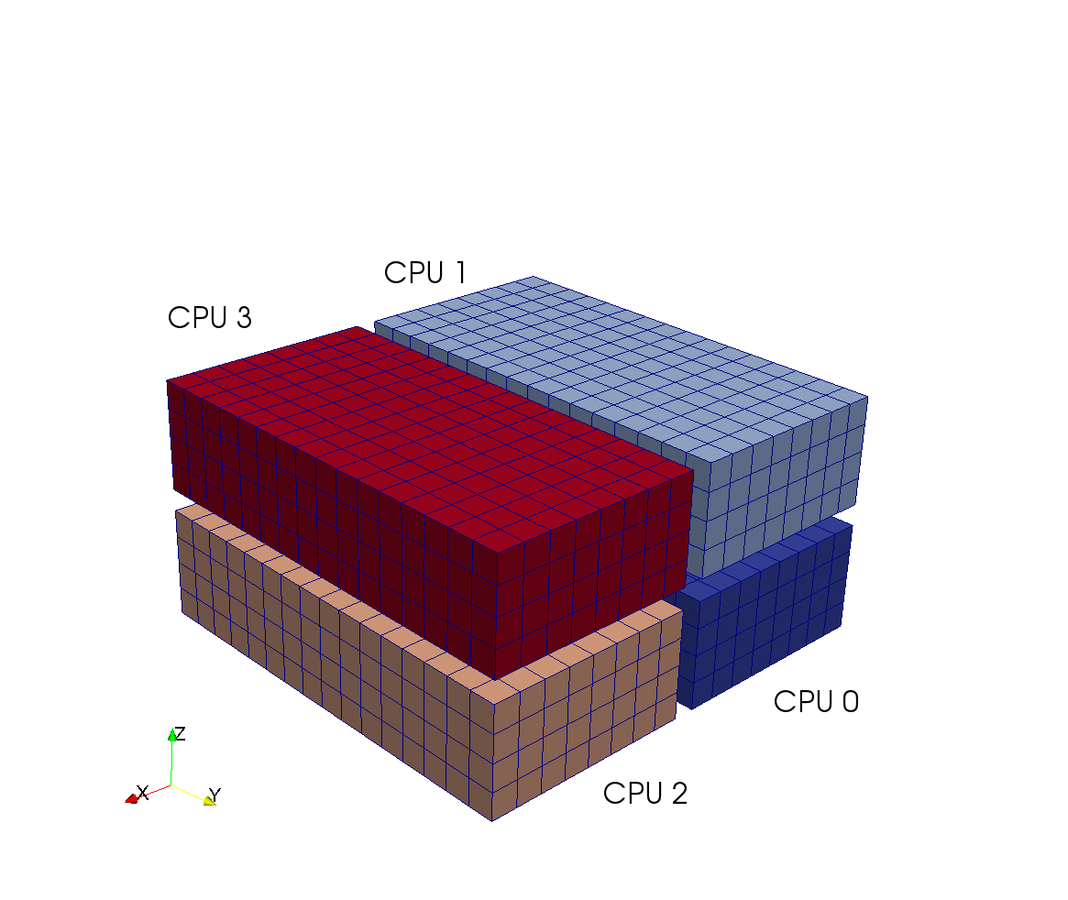
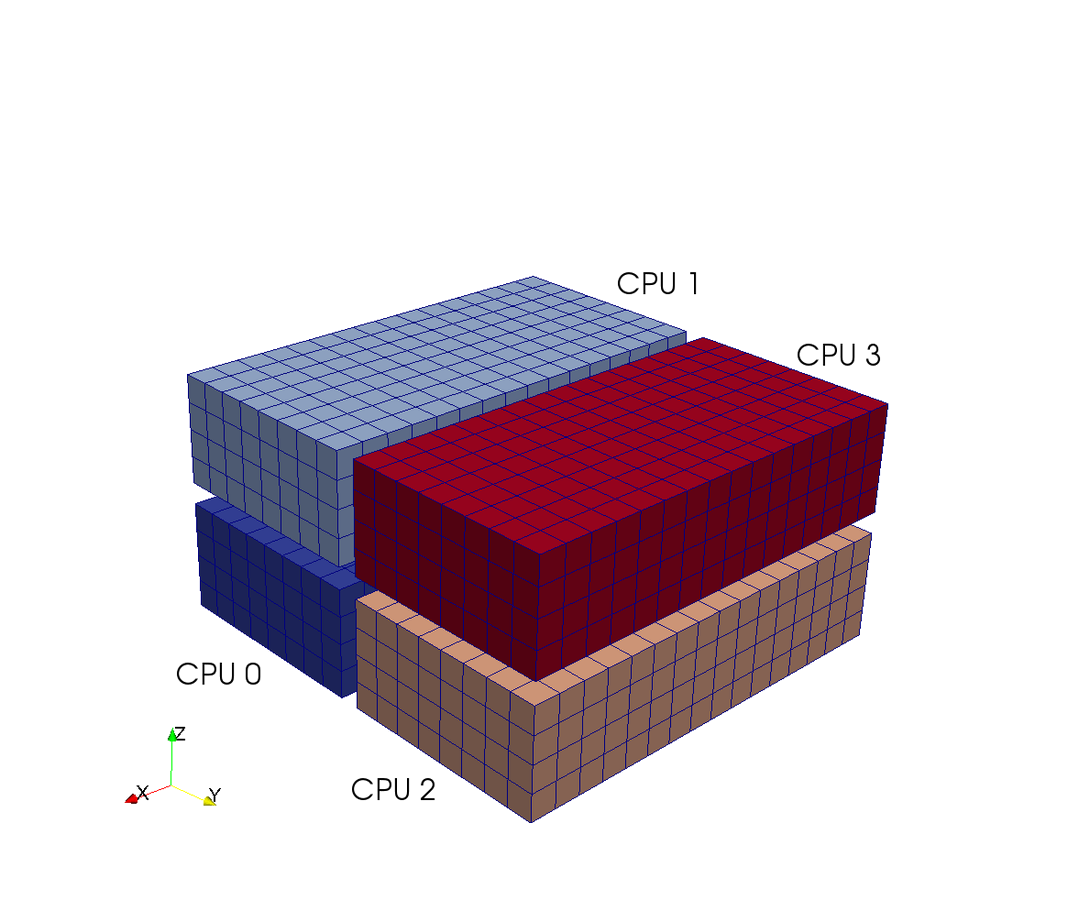
A computational box (mesh) needs to be distributed between a (possibly) large number of processors 

N^3, N \sim 1000 - 10000
N3,N∼1000−10000N^3, N \sim 1000 - 10000

Mesh size:

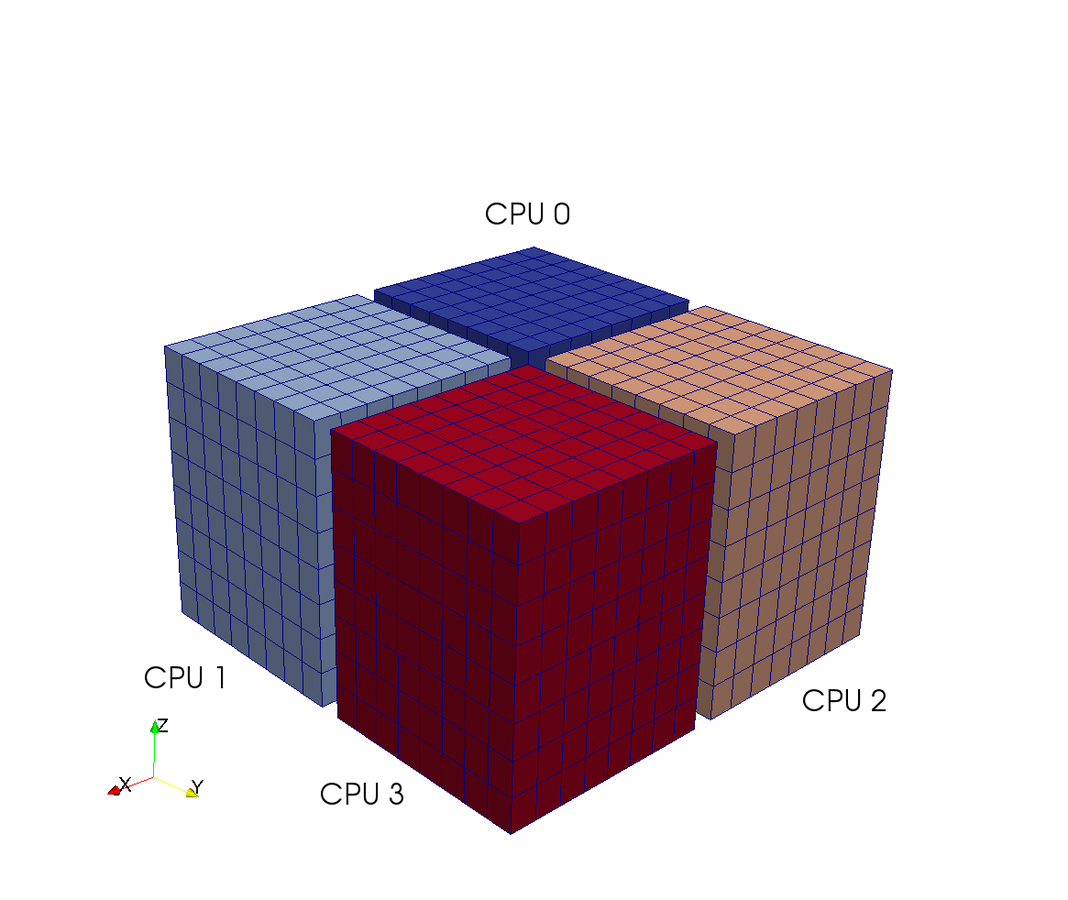
Pencil 

Slab

\le N^2
≤N2\le N^2

CPUs

\le N
≤N\le N

CPUs

mpi4py

wraps almost the entire MPI library and handles distribution of numpy arrays at the speed of C

from mpi4py import MPI
comm = MPI.MPI_COMM_WORLD
print "Hello World from rank", comm.Get_rank()
>>> mpirun -np 1000 python HelloWorld.py

Hello World from rank 0
Hello World from rank 1
Hello World from rank 3
...

MPI is basically needed to do 3D forward and backward FFT

HelloWorld.py:

3D FFT with MPI

Slab decomposition (max N CPUs)

def fftn_mpi(u, fu):
    """FFT in three directions using MPI."""
    Uc_hatT[:] = rfft2(u, axes=(1,2))
    for i in range(num_processes): # Np = N / num_processes
        U_mpi[i] = Uc_hatT[:, i*Np:(i+1)*Np]
    comm.Alltoall([U_mpi, mpitype], [fu, mpitype])    
    fu = fft(fu, axis=0)
    return fu

With serial pyfftw (wrap of FFTW) and

5 lines of Python code!

real FFT in z, complex in y

 

No MPI required

Transpose and distribute

Then FFT in last direction

There are a few low level 3D FFT modules with MPI (e.g., libfftw, P3DFFT) but none that have been wrapped or is easily called from  python

Need to adapt single core FFT

(numpy.fft, scipy.fftpack, pyfftw)

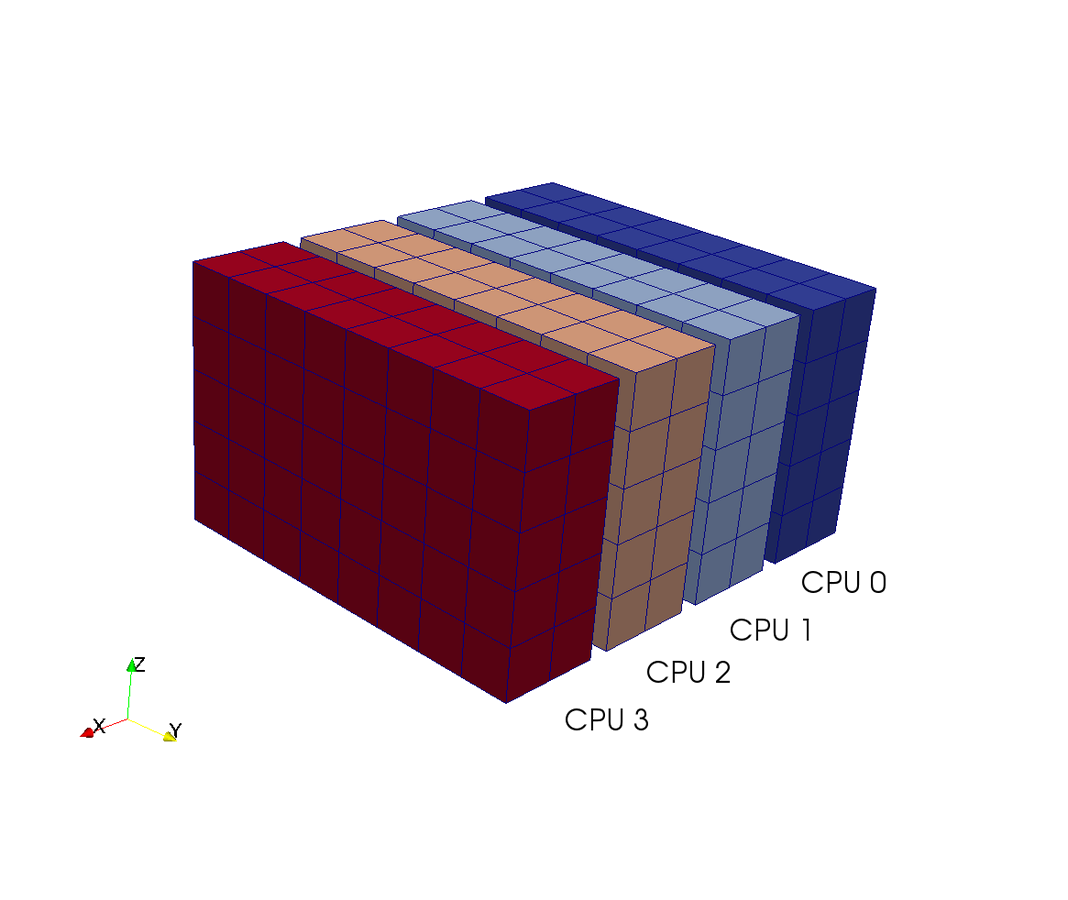
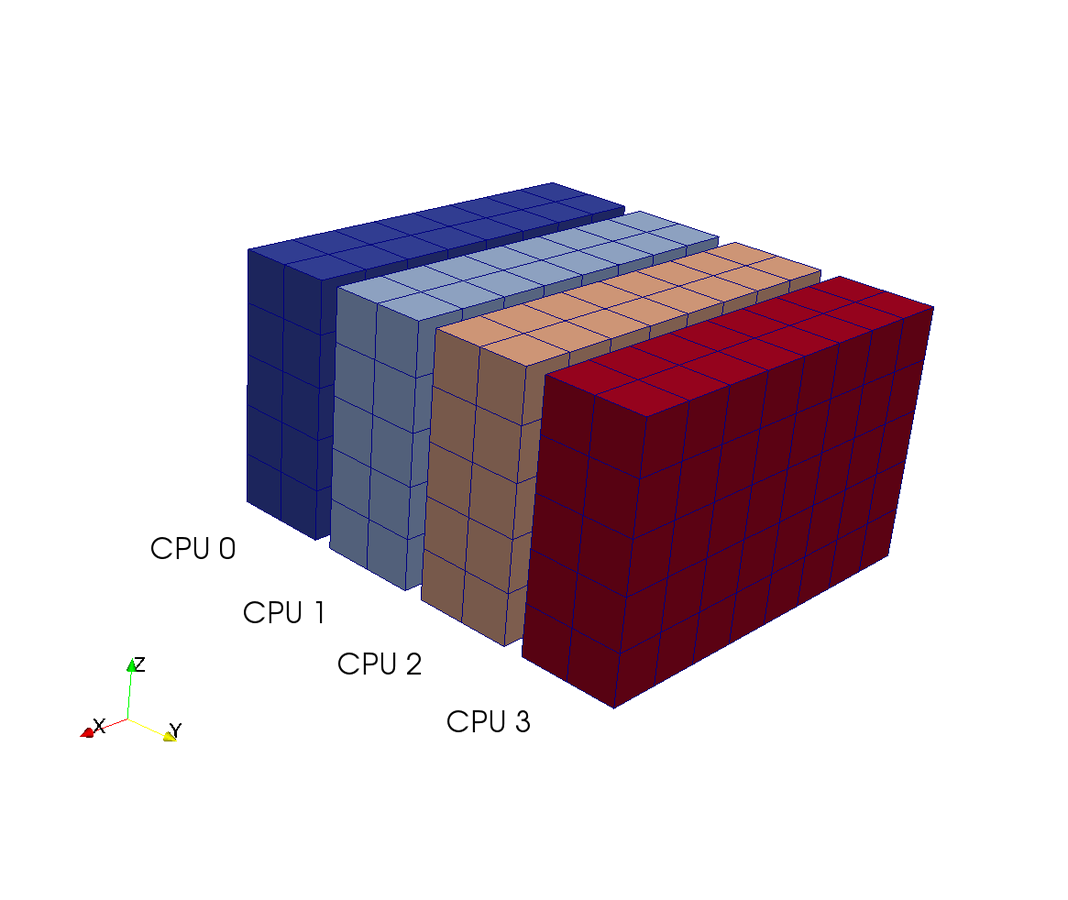
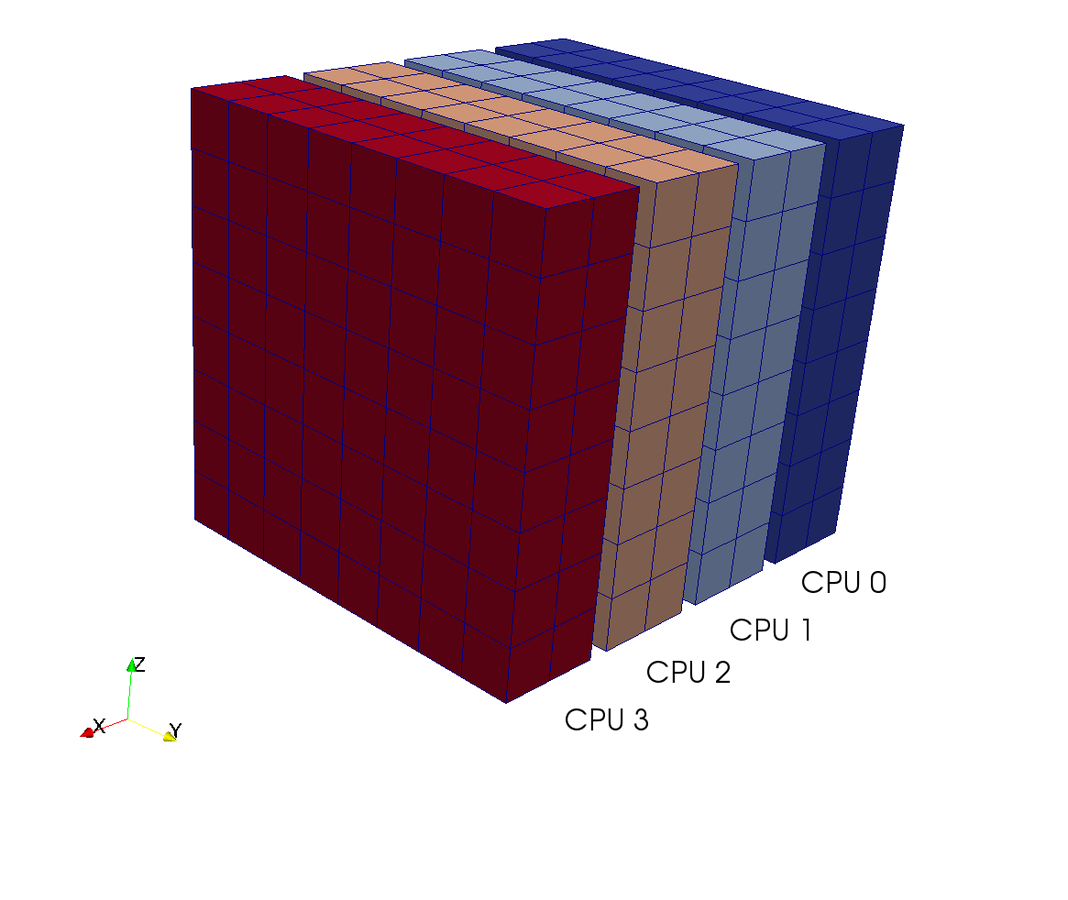
Pencil decomposition

Up to      CPUs

10 lines of Python code

to do 3D FFT with MPI

rfft(u, axis=2)

Transform

fft(u, axis=1)

Transform

 

fft(u, axis=0)

N^2
N2N^2

Numpy ufuncs responsible for most remaining cost

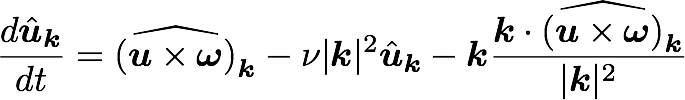
# Preallocated distributed arrays. Create array of wavenumbers
K  = array(meshgrid(kx, ky, kz, indexing='ij'), dtype=float)
K2 = sum(K*K, 0, dtype=float) # Wavenumber magnitude
dU = zeros((3, N[0], Np[1], Nf), dtype=complex) # Rhs array
    
# Subtract contribution from diffusion to rhs array
dU -= nu*K2*U_hat

Besides FFT the major computational cost is computing the right hand side using element-wise numpy ufuncs (multiplications, subtractions over the entire mesh)

Very compact code

Explicit solver

Parallell scaling

Shaheen Blue Gene P supercomputer at KAUST Supercomputing Laboratory

Testing with a transient Taylor Green flow

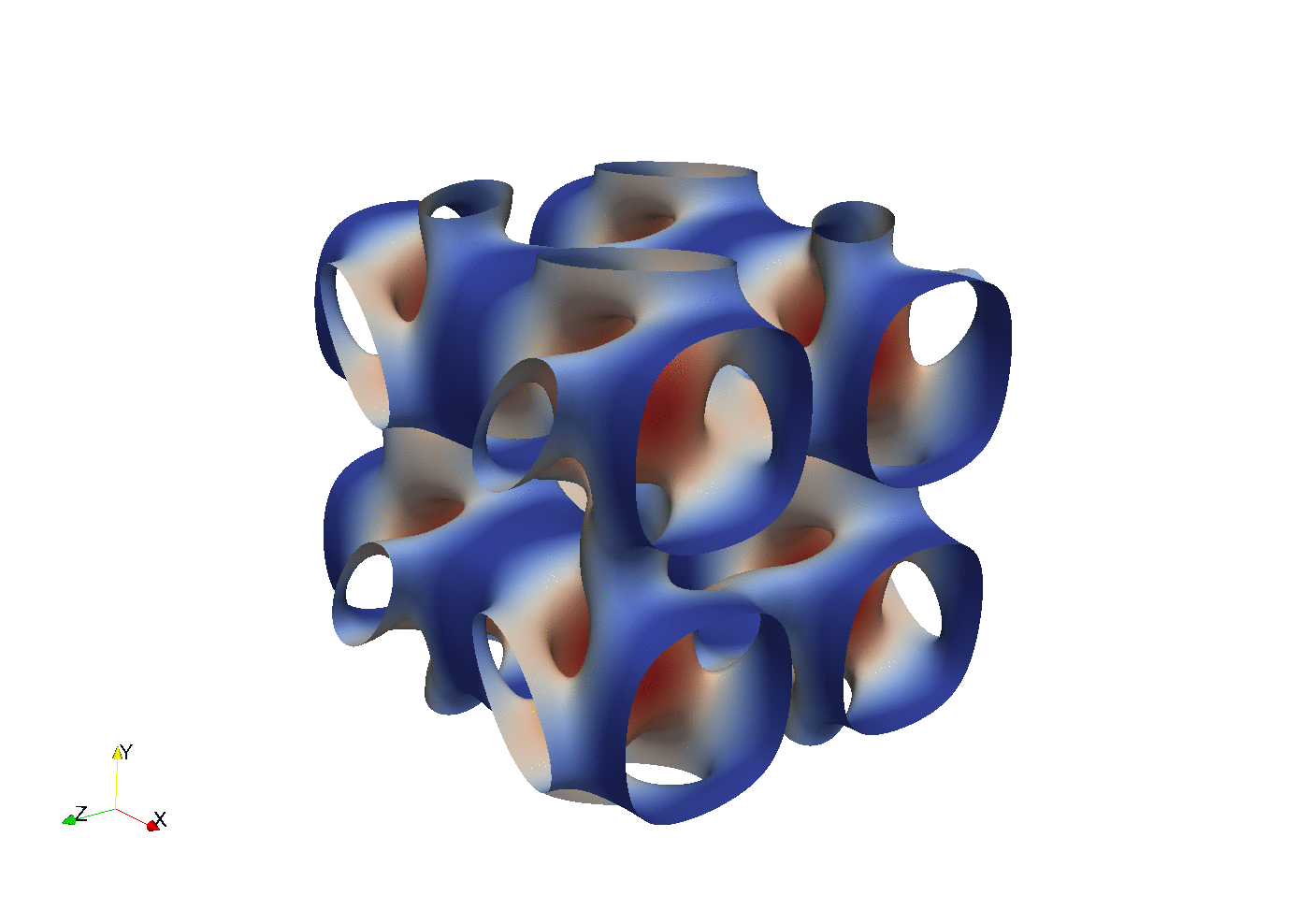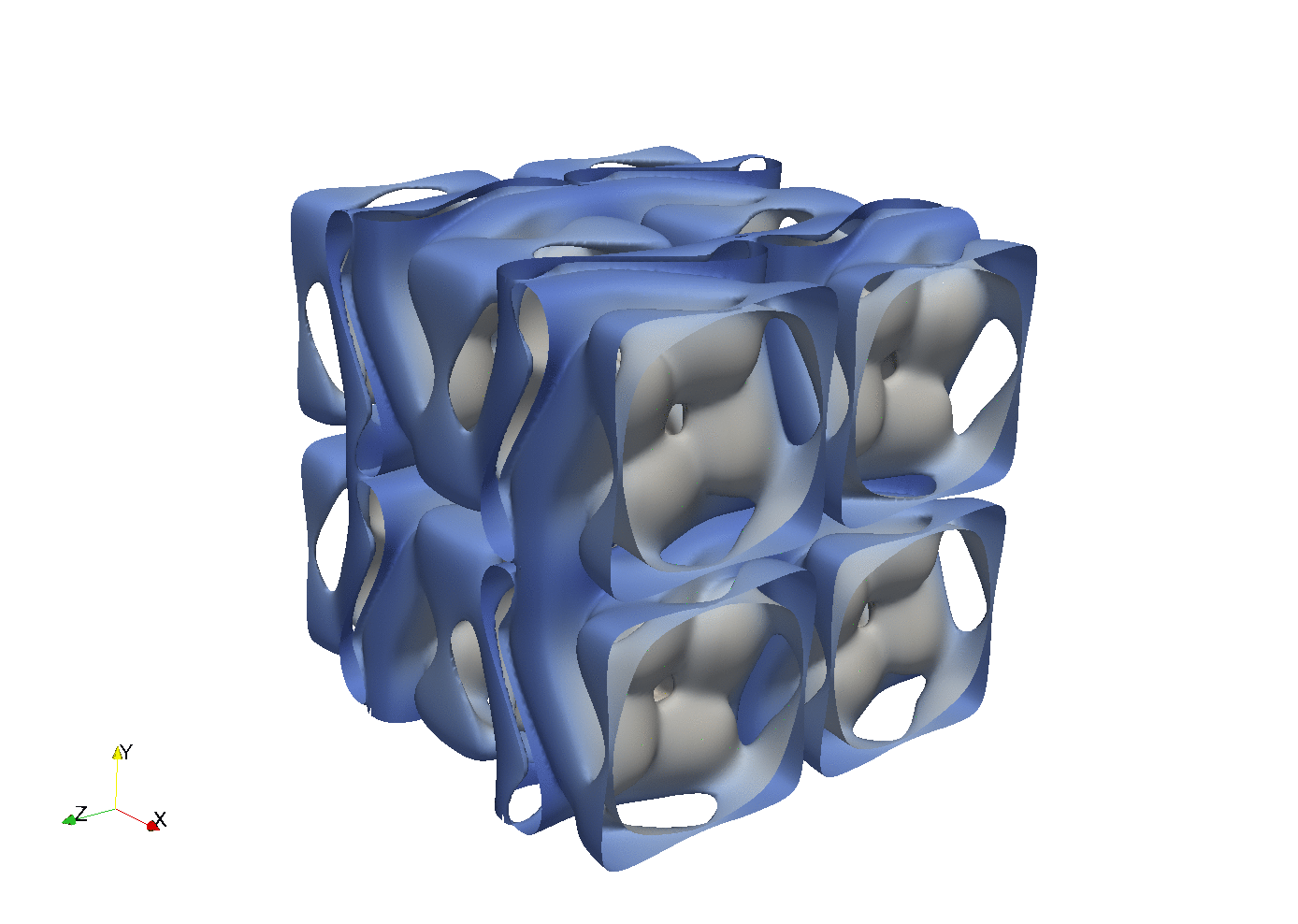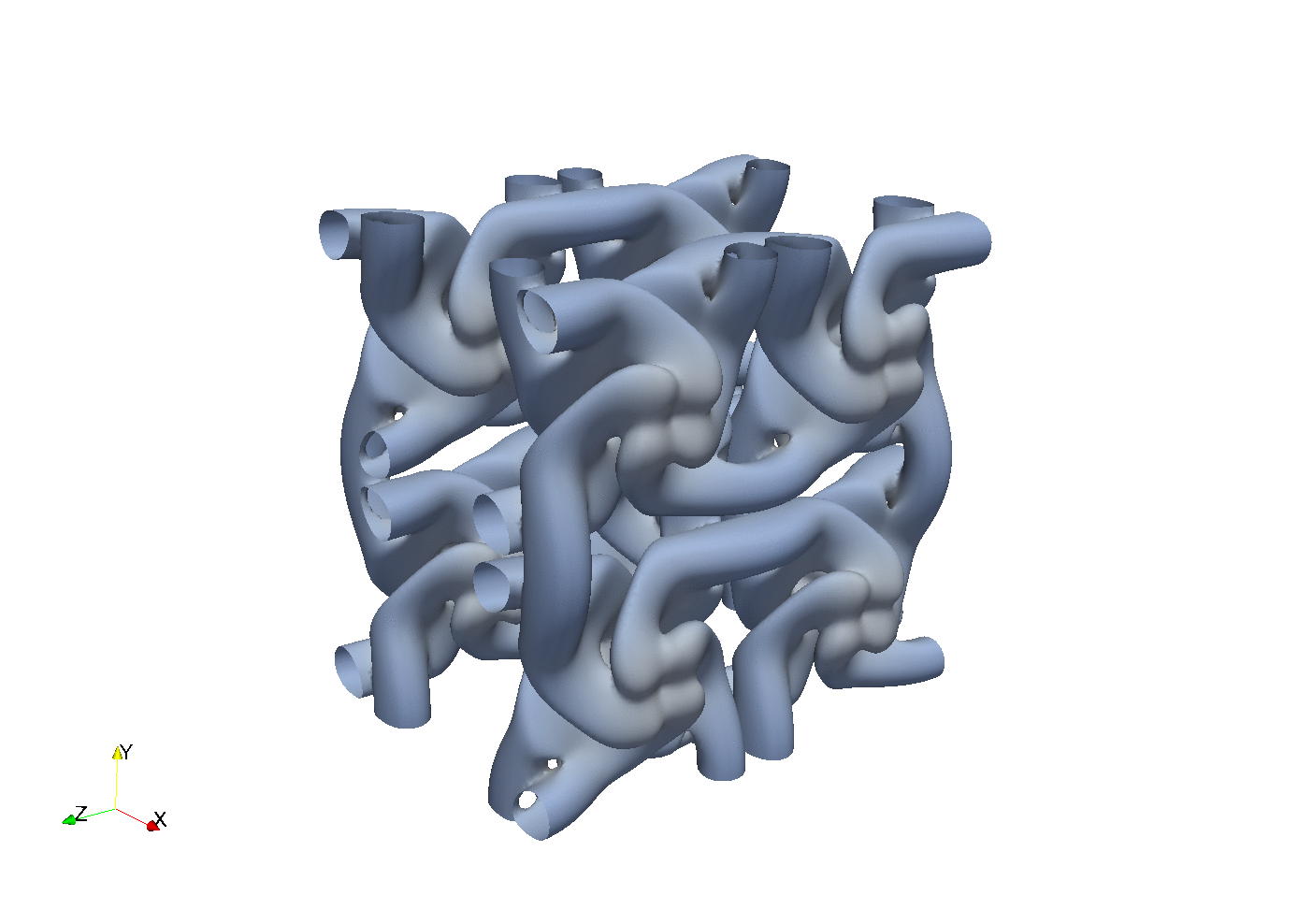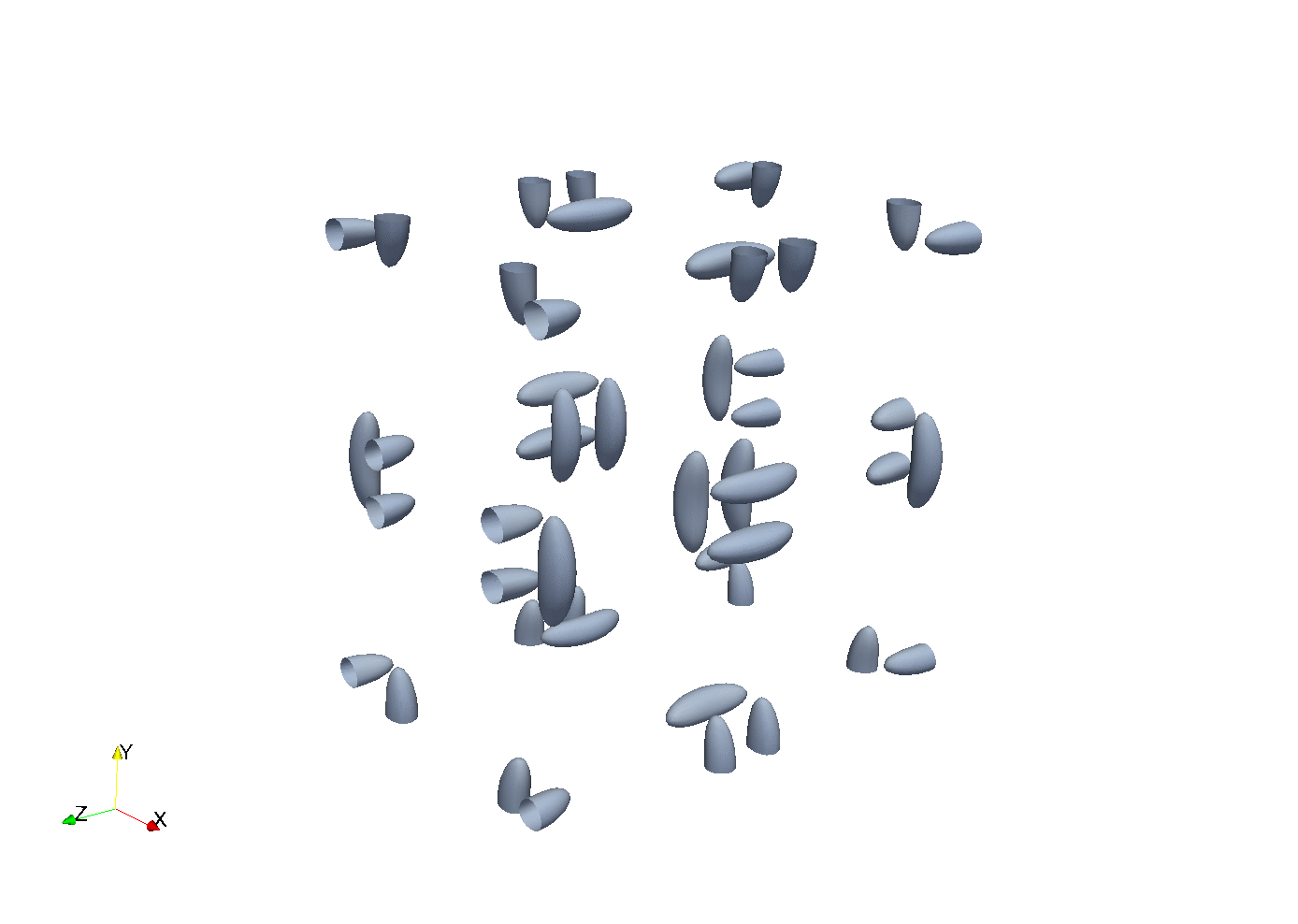
Enstrophy colored by pressure

The solver has been verified to be implemented correctly, but how does the pure numpy/mpi4py/pyfftw perform?

Parallell scaling

Shaheen Blue Gene P supercomputer at KAUST Supercomputing Laboratory

Testing the 100 lines of pure Python code

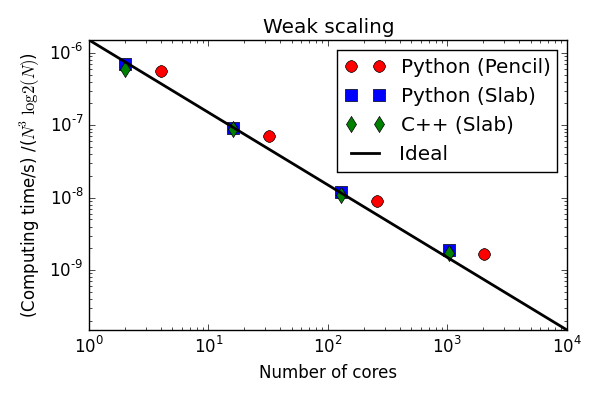
C++(slab) 30-40 % faster than Python (slab)

Python solvers struggling with the strong scaling

2048^3
204832048^3

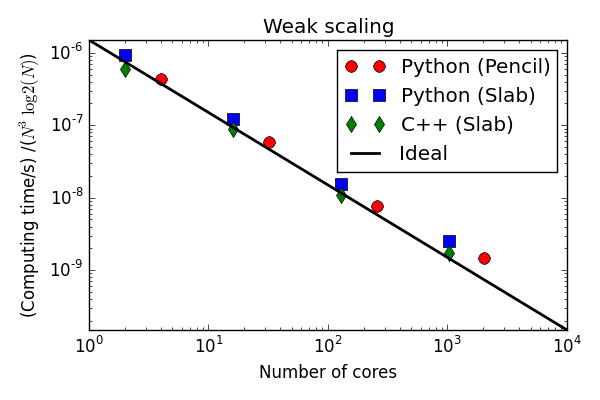
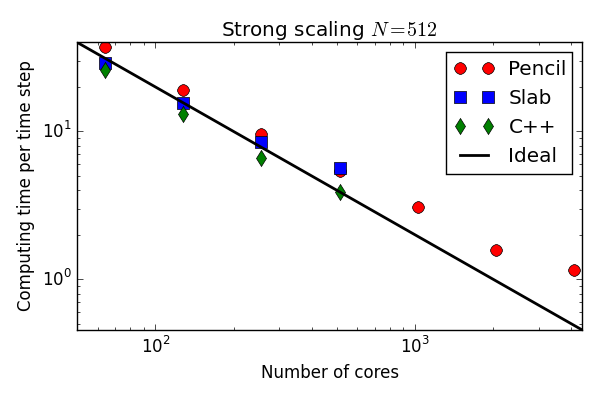
Why is the Python solver not scaling better?

def fftn_mpi(u, fu):
    """FFT in three directions using MPI."""
    Uc_hatT[:] = rfft2(u, axes=(1,2))
    for i in range(num_processes): # Np = N / num_processes
        U_mpi[i] = Uc_hatT[:, i*Np:(i+1)*Np]
    comm.Alltoall([U_mpi, mpitype], [fu, mpitype])    
    fu = fft(fu, axis=0)
    return fu

All MPI communication is found in the 3D FFTs

There's a for-loop used to transform datastructures

that I could not get rid of...

Increasingly worse for larger number of processors

Why slower than C++?

The for-loop int the FFT is one obvious thing

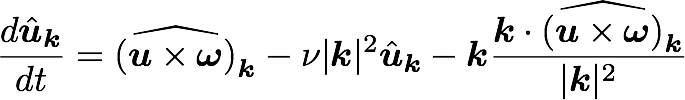
However, the ufuncs are the main cause,

at least for small number of CPUs

Numpy ufuncs not always great

def cross(a, b, c):
    """Regular c = a x b, with vector component in axis 0."""
    #c = numpy.cross(a, b, axis=0) # Alternative
    c[0] = a[1]*b[2]-a[2]*b[1]
    c[1] = a[2]*b[0]-a[0]*b[2]
    c[2] = a[0]*b[1]-a[1]*b[0]
    return c

N = 200
U = zeros((3, N, N, N))
W = zeros((3, N, N, N))
F = zeros((3, N, N, N))
F = cross(U, W, F)

Consider the cross product (required for rhs):

Too many ufuncs (multiplications, subtractions) are being called and too many temp arrays are created

Commented out regular numpy.cross is also using ufuncs and is about the same speed

Getting rid of some temp arrays helps

def cross(a, b, c):
    """Regular c = a x b, with vector component in axis 0."""
    c[0]  = a[1]*b[2]
    c[0] -= a[2]*b[1]
    c[1]  = a[2]*b[0]
    c[1] -= a[0]*b[2]
    c[2]  = a[0]*b[1]
    c[2] -= a[1]*b[0]    
    return c

Approximately 30% faster (for N=200),

but still too many ufuncs being called. Too many loops over the large 4D arrays a, b, c

Only viable solution

is to hardcode the cross product into one single loop

@jit(float[:,:,:,:](float[:,:,:,:], float[:,:,:,:], float[:,:,:,:]), nopython=True)
def cross(a, b, c):
    for i in xrange(a.shape[1]):
        for j in xrange(a.shape[2]):
            for k in xrange(a.shape[3]):
                a0 = a[0,i,j,k]
                a1 = a[1,i,j,k]
                a2 = a[2,i,j,k]
                b0 = b[0,i,j,k]
                b1 = b[1,i,j,k]
                b2 = b[2,i,j,k]
                c[0,i,j,k] = a1*b2 - a2*b1
                c[1,i,j,k] = a2*b0 - a0*b2
                c[2,i,j,k] = a0*b1 - a1*b0
    return c

Cython, Numba or Weave will all do the trick

Numba and Cython perform approximately the same

and as fast as C++!

Approximately 5 times faster than original

Solver optimized with Cython

More than matches C++ on the Blue Gene P!

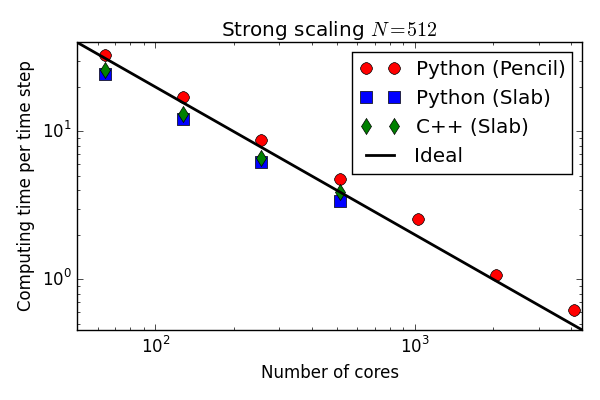
(Numba you say? You try to install Numba on a Blue Gene)

Final word of warning

Dynamic loading of Python can be very slow on supercomputers

  • With regular Python 2.7 it takes 15 minutes just to get started on a full rack (4096 CPUs) on the Blue Gene/P
  • In this work I have used Scalable Python (Python 2.6.7 with MPI-modified I/O) developed by J. Enkovaara and co-workers, which takes approximately 30 seconds to load.

Scalable Python Used to be at https://gitorious.org/scalable-python, but now I don't know?

Summary

  • A pure Python DNS solver for turbulent flows can be created from scratch with less than 100 lines of Python code!
  • This code can run on thousands of processors with billions of unknowns and almost (30-40% slower) as fast as pure C++
  • With a few routines moved to Cython, the Python based solver matches the performance of C++
  • Interested in helping out? Think you can do better?
    • https://github.com/mikaem/spectralDNS
    • Currently DNS solvers for incompressible/variable density Navier Stokes and Magneto Hydro Dynamics Isotropic (triply periodic) and channel flows

Thanks also to Hans Petter Langtangen at UiO/Simula 

and David Ketcheson at KAUST

Thank you for your attention!

Made with Slides.com